Similar presentations:
Геометрические тела, площади их поверхностей и объемы
1.
2.
Призма:- прямая и наклонная;
- прямоугольный параллелепипед.
Пирамида:
- пирамида;
- площадь пирамиды
- усеченная пирамида
- площадь усечённой пирамиды
Цилиндр
Конус :
- конус;
- усеченный конус.
Сфера, шар, части шара:
- шар;
- шаровой сегмент;
- шаровой пояс;
- шаровой сектор
Объёмы геометрических тел:
Объём призмы
Объём пирамиды
Объём усечённой пирамиды
Объём цилиндра
Объём конуса
Объём усечённого конуса
Объём шара
Объём шарового сегмента
Объём шарового слоя
Объём шарового сектора
3.
ПрямаяНаклонная
Содержание
4.
I Боковые грани равны между собойII Двугранные углы при них равны
между собой
III Любая точка оси призмы
равноудалена от всех вершин любого
из оснований призмы
IV Любая точка оси равноудалена от
всех граней призмы
Содержание
5.
6.
Площадь боковой поверхности призмыравна произведению периметру сечения,
перпендикулярного боковым рёбрам призмы
на длину бокового ребра
Sбок Pсеч
Содержание
7.
Площадь полной поверхности призмыравна сумме площадей боковой поверхности и
площадям оснований
Sполн Sбок 2Sосн
Содержание
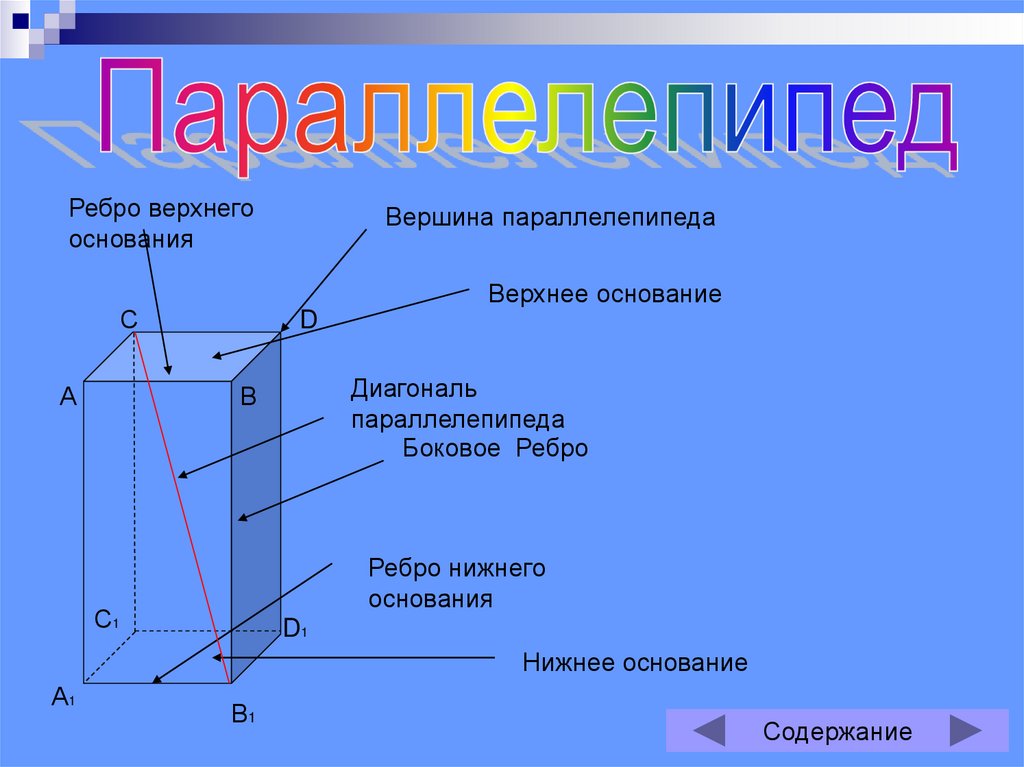
8.
Ребро верхнегооснования
Верхнее основание
С
А
Вершина параллелепипеда
D
Диагональ
параллелепипеда
Боковое Ребро
В
Ребро нижнего
основания
С1
D1
Нижнее основание
А1
В1
Содержание
9.
S бок lPоснСодержание
10.
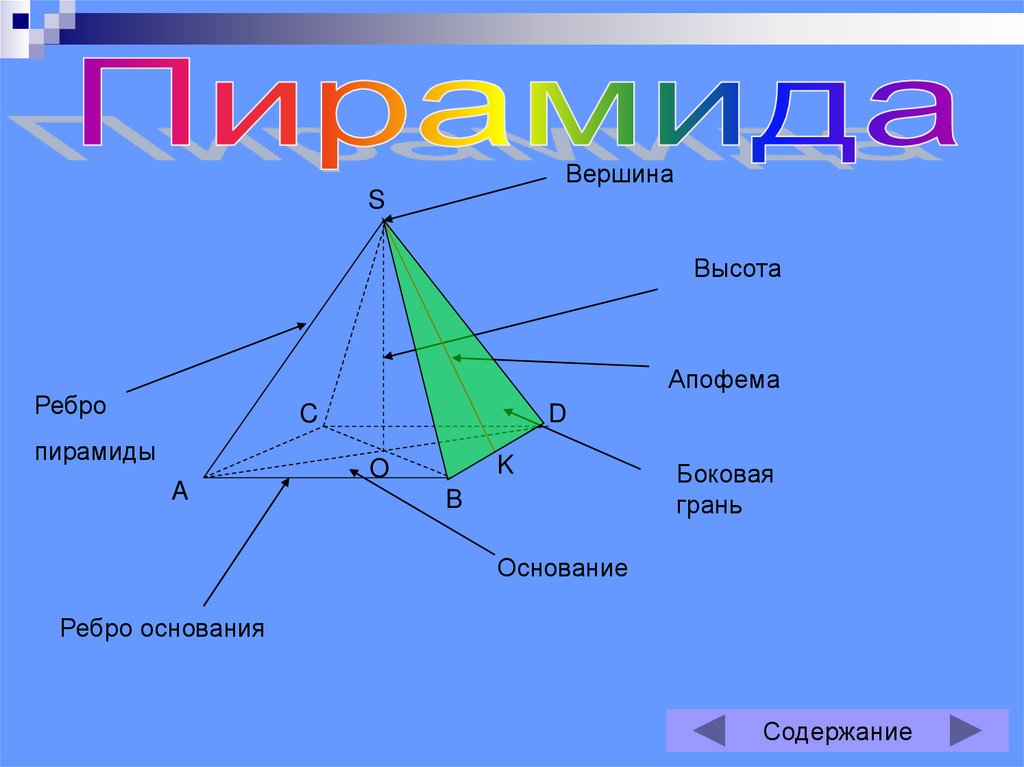
ВершинаS
Высота
Апофема
Ребро
C
пирамиды
A
D
K
O
B
Боковая
грань
Основание
Ребро основания
Содержание
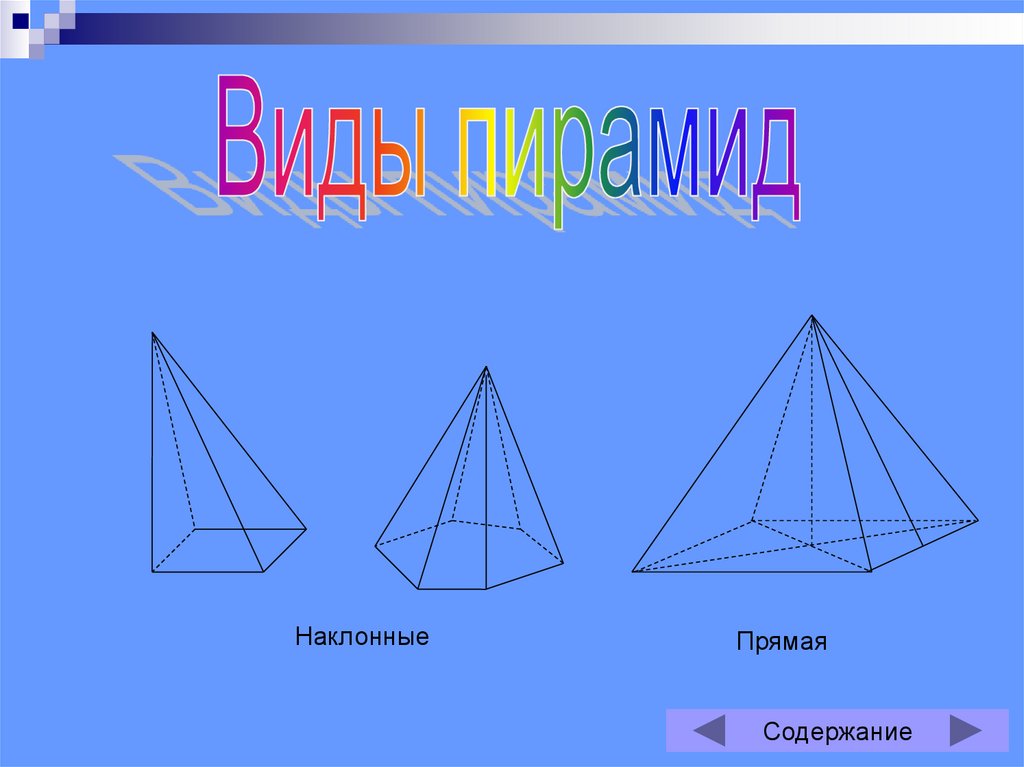
11.
НаклонныеПрямая
Содержание
12.
I Боковые ребра, грани и апофемысоответственно равны.
II Двугранные углы при основании равны.
III Двугранные углы при боковых ребрах
равны.
IV Каждая точка высоты равноудалена от
всех вершин основания.
V Каждая точка высоты равноудалена от всех
боковых граней.
Содержание
13. Площадь пирамиды
S бок1
Pa
2
Где a – апофема
P – периметр основания
Sполн Sбок Sосн
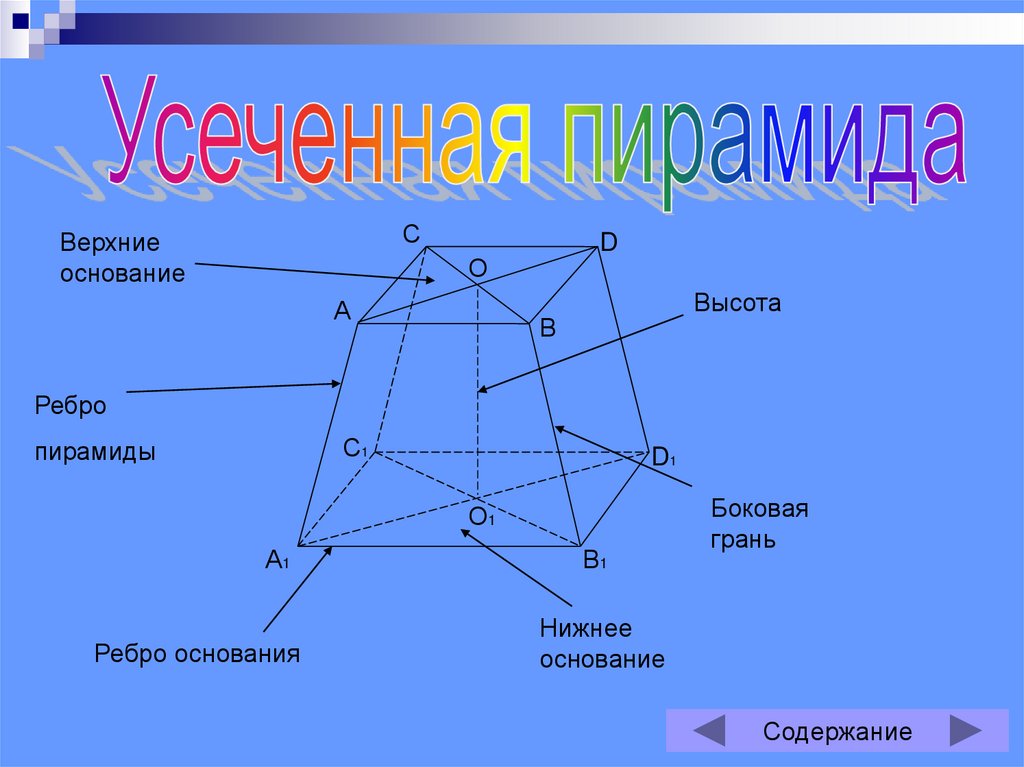
14.
СВерхние
основание
D
О
А
Высота
В
Ребро
С1
пирамиды
D1
О1
А1
Ребро основания
В1
Боковая
грань
Нижнее
основание
Содержание
15. Площадь усечённой пирамиды
S бок1
( P P1 ) a
2
Где, P – периметр нижнего основания
P1 – периметр верхнего основания,
А - апофема
S полн S бок S верхн.осн S нижн.осн
16.
I Боковые рёбра, боковые грани и апофемысоответственно равны.
II Двугранные углы при основании равны.
III Двугранные углы при боковых рёбрах
равны.
IV Каждая точка оси равноудалена от всех
вершин основания.
V Каждая точка оси равноудалена от
плоскостей боковых граней.
Содержание
17.
Радиусверхнего
основания
О1
Верхнее
основание
А1
Высота
Образующая
О
А
Нижнее
основание
Радиус
нижнего
основания
Содержание
18.
Sполн Sбок 2SоснS 2 R( R h)
Содержание
19.
Площадь боковой поверхностицилиндра:
S 2 Rh
Площадь основания цилиндра:
S R
2
Содержание
20.
ВершинаS
Высота
Образующая
L
L
Образующая
А
Основание
R
R
О
В
Радиус
основания
Содержание
21.
S Sсект RLСодержание
22.
Sполн R( R L)23.
Радиусверхнего
основания
Верхние
основание
R О
Высота
L
Образующая
L
Образующая
А
Основание
R
R
О1
В
Радиус
нижнего
основания
Содержание
24.
S полн ( R r ) L R r2
2
или
S полн ( LR Lr R r )
2
2
Содержание
25.
Содержание26.
Площадь поверхности сферы равнаучетверённой площади большого круга
этой сферы:
S 4 R
2
Содержание
27.
S 2 Rhh
R
Содержание
28.
S 2 RhR
h
Содержание
29.
hr
R
Содержание
30.
Содержание31.
V Sосн HСодержание
32.
SC
A
D
1
V S осн H
3
K
O
B
Содержание
33.
СD
О
А
В
С1
D1
О1
А1
В1
2
V (Sн Sв S н Sв )
3
Содержание
34.
О1А1
V R H
2
О
А
Содержание
35.
SL
А
1 2
V R H
3
L
R
R
О
В
Содержание
36.
R ОL
А
V
h
3
L
R
R
О1
В
( R r Rr )
2
2
Содержание
37.
4 3V R
3
Содержание
38.
hV R ( R )
3
2
h
R
Содержание
39.
12
2
V R H H (a ab b )
3
2
R
h
Содержание
40.
2 2V R H
3
h
r
R
Содержание













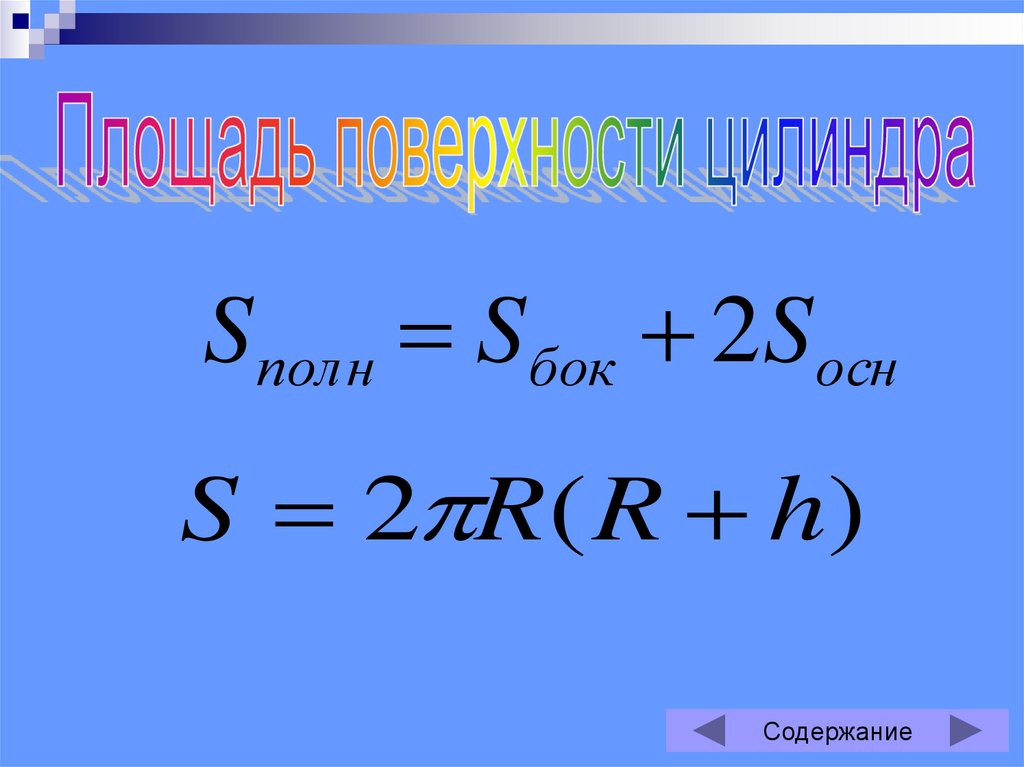






















 mathematics
mathematics








