Приложения производной

1.

2.

6. ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
6.1 Правило Лопиталя
6.2 Исследование функции и построение её графика
6.3 Нахождение наибольшего и наименьшего
значений функции

3.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
1) Найти область определения функции y = f(x).
2) Исследовать функцию на непрерывность, найти точки разрыва и
односторонние пределы в этих точках.
3) Найти асимптоты графика функции, выяснить поведение функции на
границе области определения.
4) Исследовать функцию на чётность-нечётность, периодичность.
5) Найти производную 1-го порядка, исследовать функцию на экстремум,
выписать интервалы возрастания и убывания функции.
6) Найти производную 2-го порядка, найти точки перегиба графика
функции, выписать интервалы, где график является выпуклым или
вогнутым.
7) Провести дополнительные исследования (при необходимости).
8) Все полученные данные записать в таблицу.
9) Сделать чертёж графика функции y = f(x).
Пример
Провести полное исследование функции
и построить её график.
x3
y 2
x 1

4.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
Найдём область определения:
x 2 1 0 x 2 1 x 1 D y ; 1 1;1 1;
Исследуем функцию в точках разрыва:
1 0
1 0
x3
1
lim
2
2
x 1 0 x 2 1
1 0 1 1 0 1 0
3
1 0
3
3
1 0
3
x
1
2
2
x 1 0 x 2 1
1 0 1 1 0 1 0
3
lim
x
1 0 1
2
x 1 0 x 2 1
1
0
1 0
3
Значит, х = -1 – точка
разрыва 2-го рода.
3
lim
1 0
x3
1
lim
2
x 1 0 x 2 1
1 0 1 0
3
Значит, х = 1 – точка
разрыва 2-го рода.

5.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
Получили: х = -1 и х = 1 – двусторонние вертикальные асимптоты.
Найдём наклонные асимптоты (для рациональной дроби только
двусторонние) y = kx+b :
y
x3
x2
2x
k lim lim 2
lim 2
lim
1
x x
x x 1 x
x x 1
x
2x
x x x 1
x3
x3 x3 x
b lim 2
1 x lim
lim
2
2
x x 1
x
x
x 1
x 1
3
2
x
1
1
lim
0
x x 2 1
x
2x
lim
Получили: у = х – двусторонняя наклонная асимптота.

6.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
Исследуем чётность-нечётность:
D y ; 1 1;1 1; – симметрична относительно 0
x
3
x3
y x
2
y x функция нечётная
2
x 1 x 1
Исследуем периодичность:
Это элементарная функция и она не является тригонометрической,
поэтому она не периодическая.

7.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
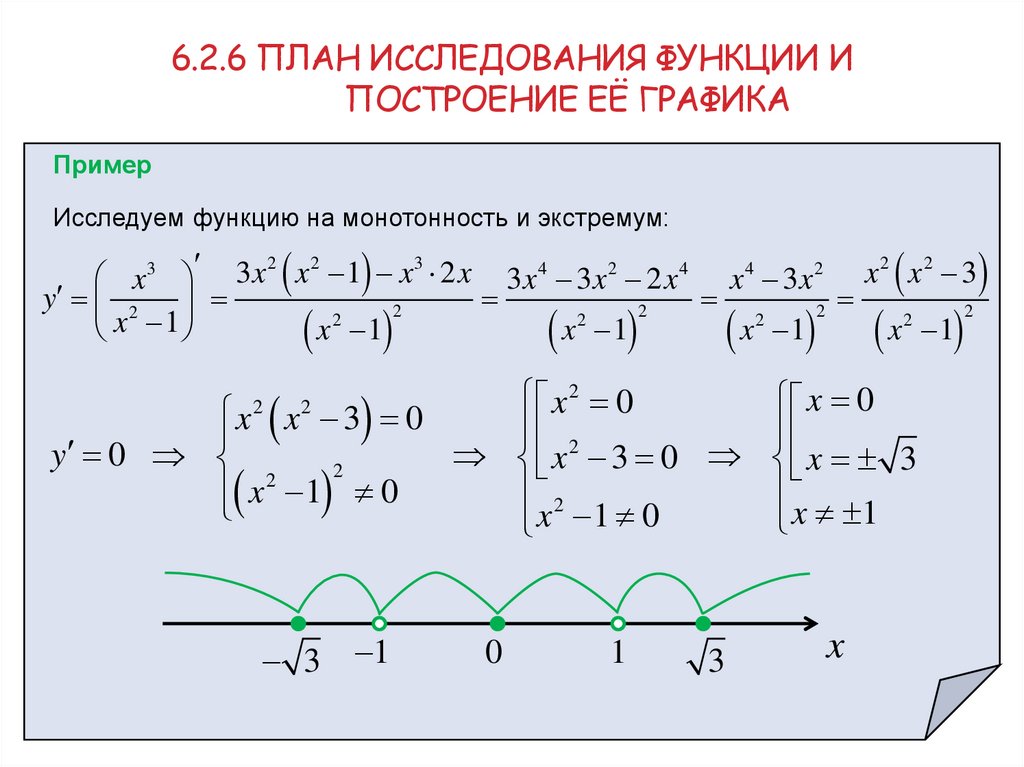
Исследуем функцию на монотонность и экстремум:
2
2
3
2
2
x3 3x x 1 x 2 x 3x 4 3x 2 2 x 4 x 4 3x 2 x x 3
y 2
2
2
2
2
2
2
2
2
x
1
x 1
x 1
x 1 x 1
2
x 0
x
0
x x 3 0
2
y 0
x 3 0
x 3
2
2
x 1 0
2
x 1
x 1 0
2
2
3 1
0
1
3
x

8.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
y
x 2 x 2 3
x 1
2
2
Знак производной зависит только
от множителя
2
x
3 .
2 3 4 3 1 0
y 2 0
x 2
2 3 2 3 1 0
y 2
x 0,5
0,5 3 0, 25 3 2,75 0 y 0,5 0
x 2
2
2
2
0

9.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
и x 3; .
x 3; 1 , 1;0 , 0;1 и 1; 3 .
x ; 3
Функция возрастает при
Функция убывает при
x 3 – точка максимума
x 3
– точка минимума
3
3 3
y y 3
2,6 – максимум функции.
3 1 2
3
3 3
y y 3
2,6 – минимум функции.
3 1 2
3
max
2
3
min
2

10.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
Исследуем функцию на выпуклость, вогнутость и перегибы:
2
3
2
4
2
4 x 6 x x 1 x 4 3x 2 2 x 2 1 2 x
x
3
x
y
2
4
2
2
x 1
x 1
x 1 2 x 2 x 3 x 1 x 3 x 4 x
x 1
2 x 2 x 3 x 1 x 3 x 2
x 1
2 x 2 x 3x 2 x 3 2 x 6 x 2 x x 3
x 1
x 1
2
2
2
4
4
2
2
2
4
2
2
2
2
3
2
4
2
4
3
2
2
2
3

11.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
2 x x 2 3 0
x 0
x 0
y 0
2
3
2
x 1
x 1 0
x 1 0
y
1
y
0
2 x x 2 3
x 1
2
3
1
y 2
4 4 3
28
0
27
4 1
x
1 0, 25 3 3, 25
0
y 0,5
3
3
0,75
0, 25 1
1 0, 25 3
3, 25
0
y 0,5
3
3
0, 25 1 0,75
4 4 3 28
0
y 2
3
27
4 1
3

12.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
Пример
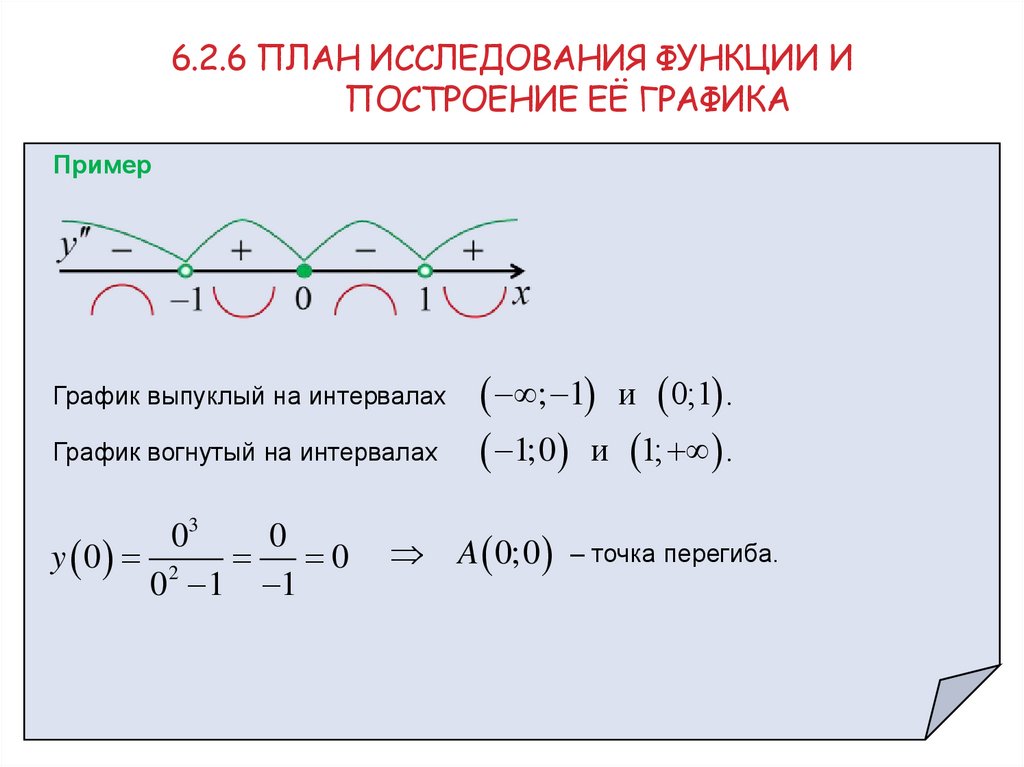
График выпуклый на интервалах
График вогнутый на интервалах
03
0
y 0 2
0
0 1 1
; 1 и 0;1 .
1;0 и 1; .
A 0;0 – точка перегиба.

13.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
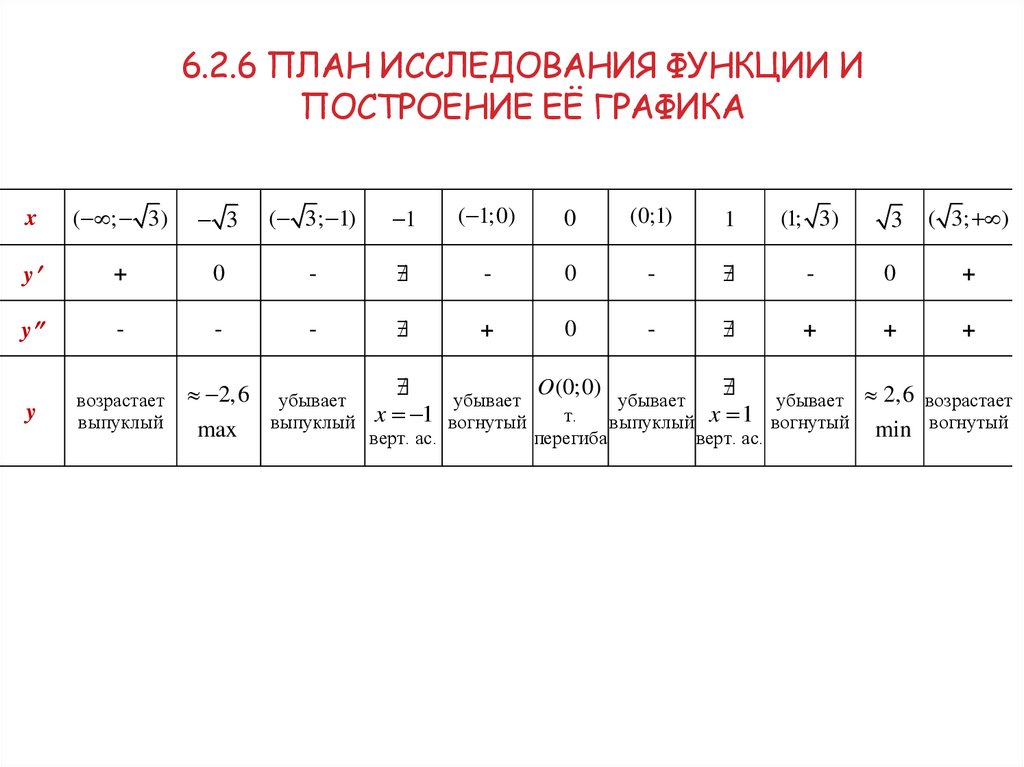
x
( ; 3)
3
( 3; 1)
1
( 1;0)
0
(0;1)
1
(1; 3)
3
( 3; )
y
+
0
-
-
0
-
-
0
+
y
-
-
-
+
0
-
+
+
+
y
возрастает
выпуклый
O(0;0)
2,6 убывает
убывает
убывает
убывает 2,6 возрастает
x 1
x 1
т.
max выпуклый верт. ас. вогнутый перегиба выпуклый верт. ас. вогнутый min вогнутый

14.

6.2.6 ПЛАН ИССЛЕДОВАНИЯ ФУНКЦИИ И
ПОСТРОЕНИЕ ЕЁ ГРАФИКА
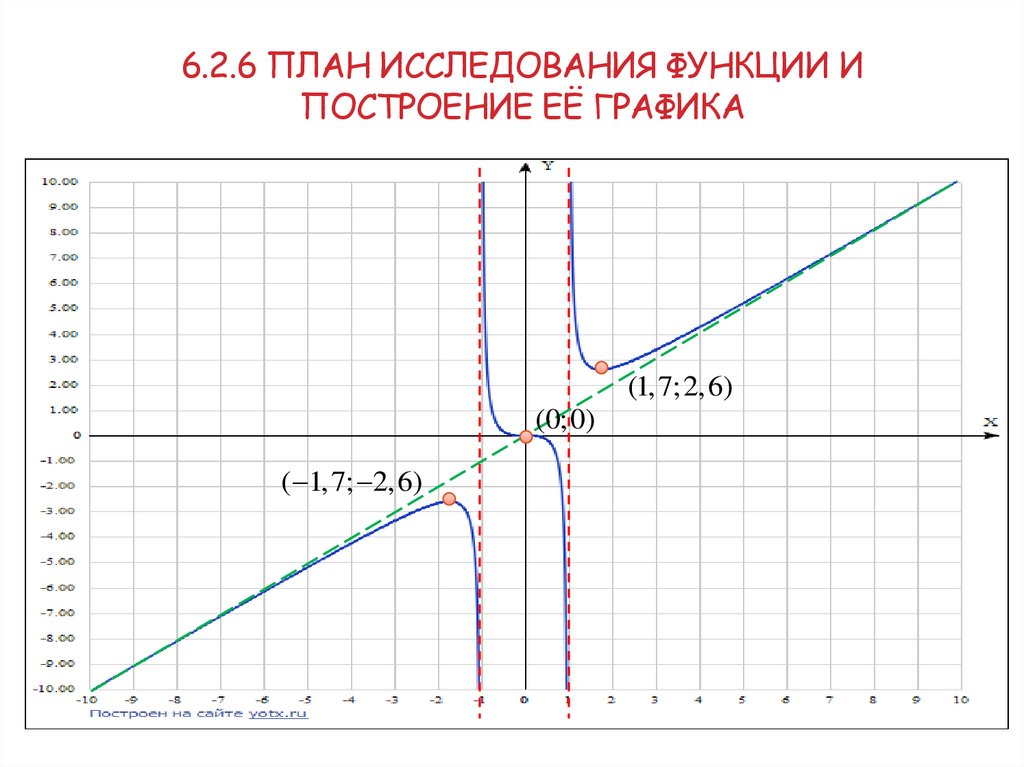
(1,7;2,6)
(0;0)
( 1,7; 2,6)

15.

ПРОДОЛЖЕНИЕ СЛЕДУЕТ...