Площадь криволинейной трапеции и интеграл

1.

Двадцать седьмое февраля
Классная работа
Площадь криволинейной
трапеции и интеграл.

2.

1.Вычислить первообразную функции:
а) у = х – 3,
б) у = 2х + 4,
в) у = 1– 4х + 15х2,
г) у = 4х3 + 12х2 – 8х,
д) y=(3х + 1)(3х – 1),
е) у = 2sin х,
ж) у = sin х – 5х.

3.

Найти С, если график первообразной,
проходит через точку М у = х + 2, М(2; 7).

4.

Вычислить определённый интеграл.
10
а) ‫׬‬0 2хdx,
21
б) ‫׬‬1 dx,
3
в) ‫׬‬−1(3х2 + 1)dx,
2
2
г) ‫׬‬0 (1 + 2х + х )dx.

5.

Вычислить площадь фигуры, ограниченной
линиями.
А) у = х, у = 0, х = 2, х = 4;
Б) у = 2х, у = 0, х = 0, х = 2;
В) у = х + 1, у = 0, х = −1 , х = 1;
Г) у = 3 − х, у = 0 х = 0, х = 3.

6.

7.

8.

9.

10.

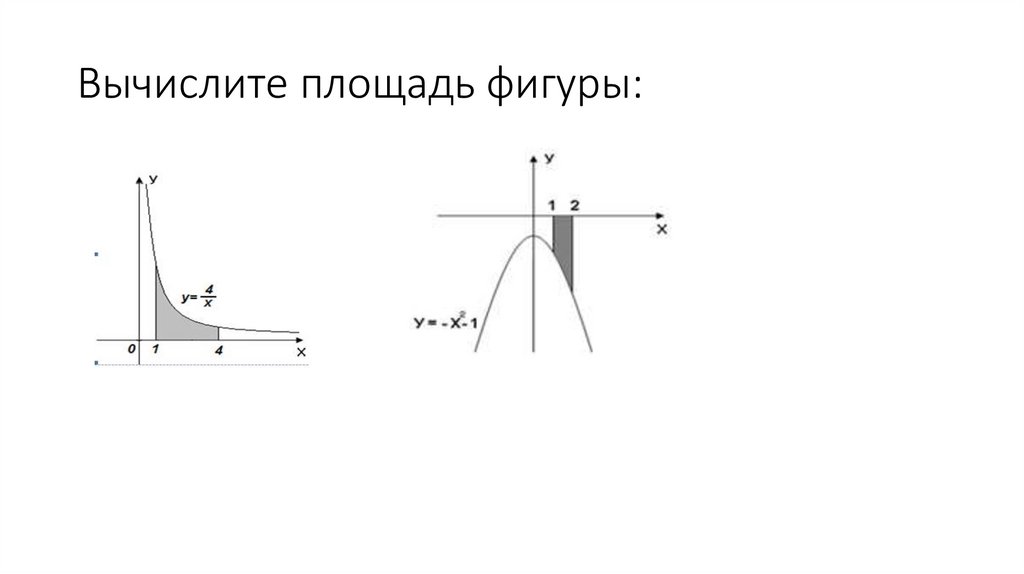
Вычислите площадь фигуры:

11.

Домашнее задание:
Выучить: § 56
1. Вычислить площадь фигуры, ограниченной
линиями.
А) у = 2 − 2х, у = 0, х = − 1, х = 1;
Б) у = 1 + 2х, у = 0, х = 0, х = 2;
В) у = 3х + 3, у = 0, х = 0, х = 1;
Г) у = 0,5х, у = 0, х = 2, х = 4.