Первообразная. Интеграл. Площадь криволинейной трапеции

1.

29.01.2022 г.
Первообразная. Интеграл.
Площадь криволинейной трапеции.
(11 класс)

2.

Определенный интеграл
b
b
f
(
x
)
dx
F
(
x
)
F
(
b
)
F
(
a
)
a
a
– формула Ньютона-Лейбница.
Геометрический смысл определенного интеграла заключается в
том, что определенный интеграл равен площади криволинейной
трапеции, образованной линиями:
сверху ограниченной кривой у = f(x),
и прямыми у = 0; х = а; х = b.

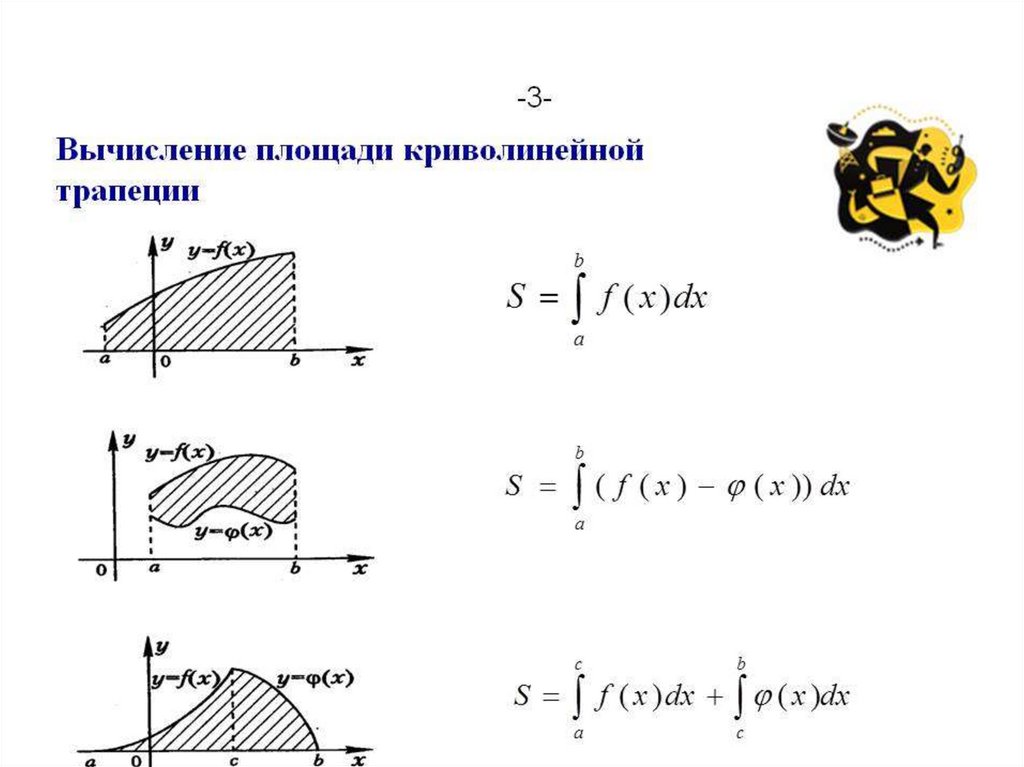
3.

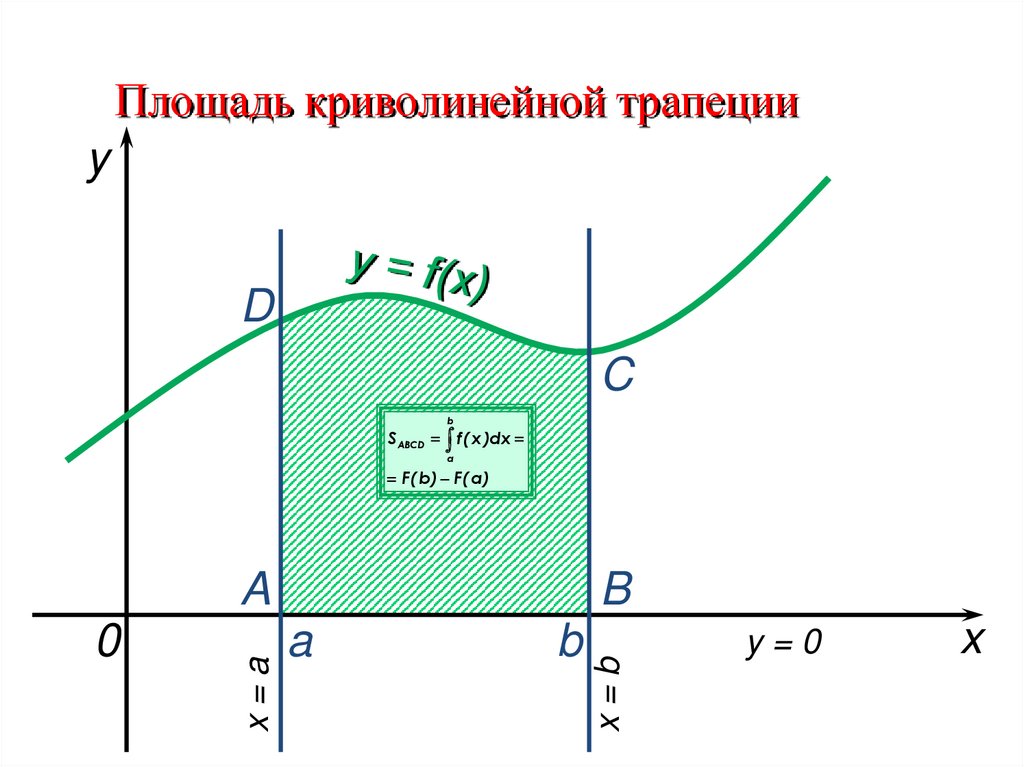
Площадь криволинейной трапеции
y
D
C
b
S ABCD f ( x )dx
a
F( b ) F( a )
B
a
b
x=b
0
x=a
A
y=0
x

4.

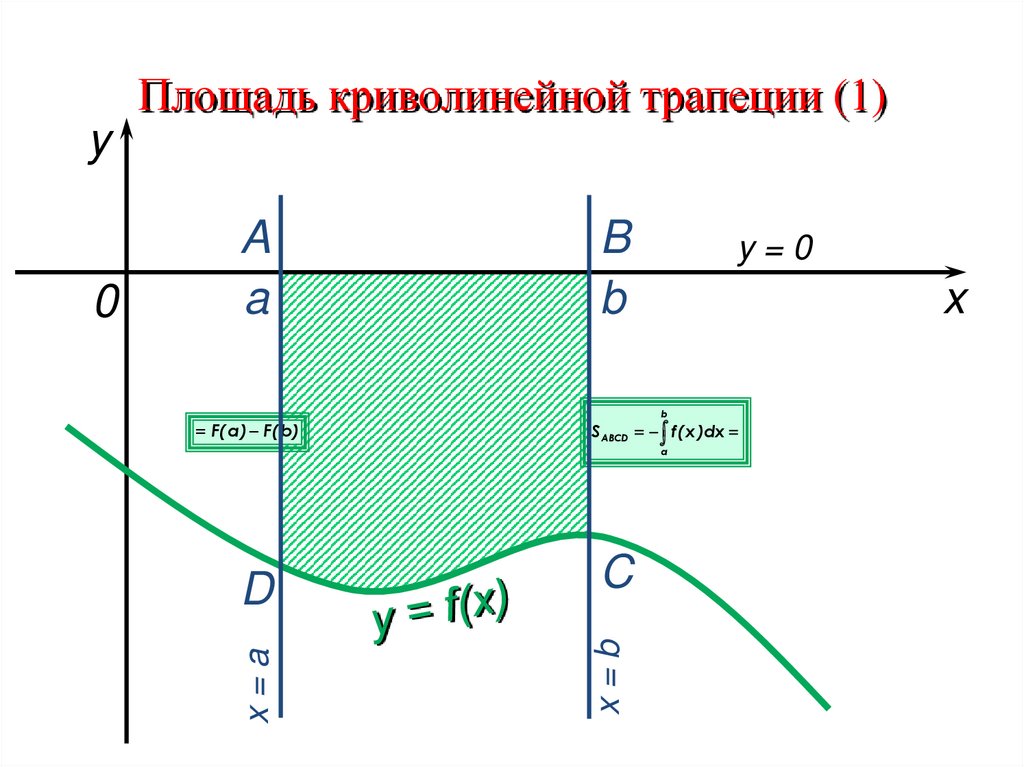
Площадь криволинейной трапеции (1)
y
B
b
y=0
x
b
F( a ) F( b )
S ABCD f ( x )dx
D
C
x=b
a
x=a
0
A
a

5.

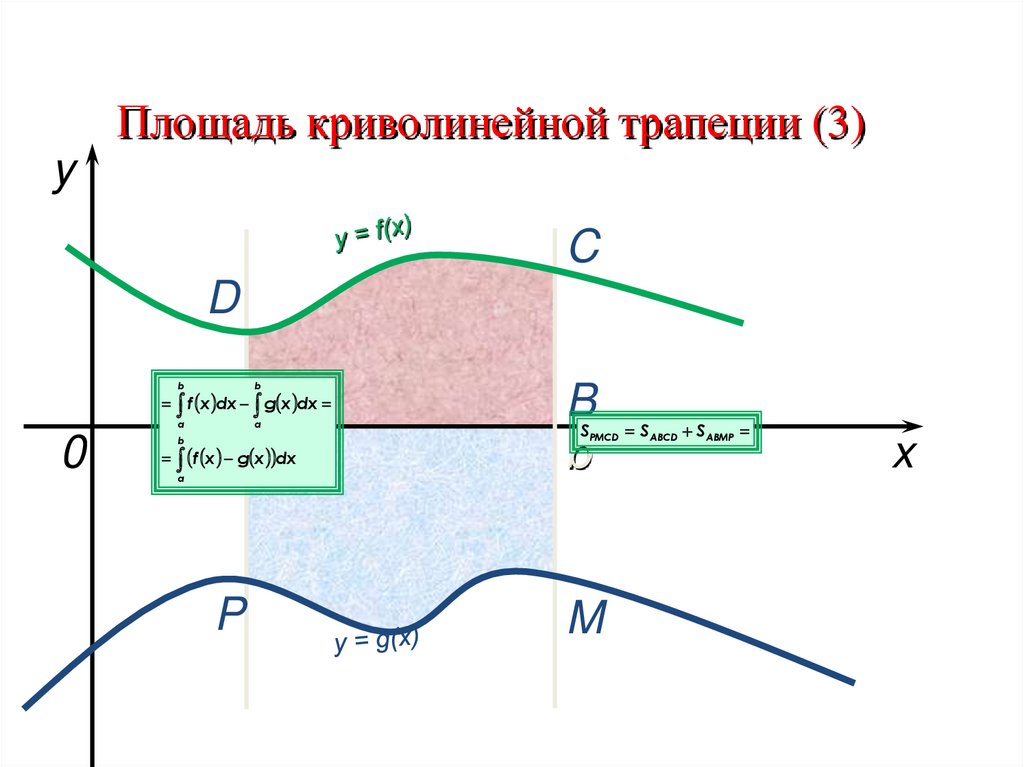
Площадь криволинейной трапеции (3)
y
C
D
b
b
a
a
A
a
B
b
P
M
f x dx g x dx
0
b
f x g x dx
a
SPMCD SABCD SABMP
x

6.

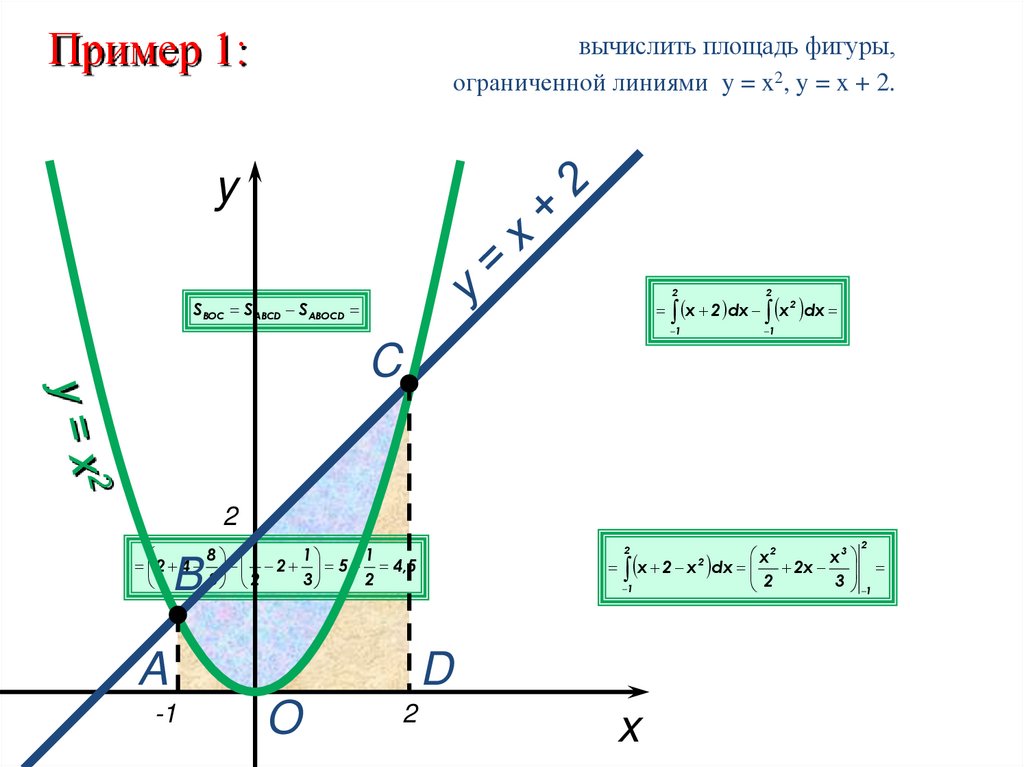
Пример 1:
вычислить площадь фигуры,
ограниченной линиями y = x2, y = x + 2.
y
SВОС SABCD SABOCD
2
2
1
1
2
x 2 dx x dx
C
2
2
8 1
1
1
2 4 2 5 4,5
3 2
3
2
B
A
-1
D
O
2
2
x2
x3
х 2 х dx 2x
3 1
2
1
x
2

7.

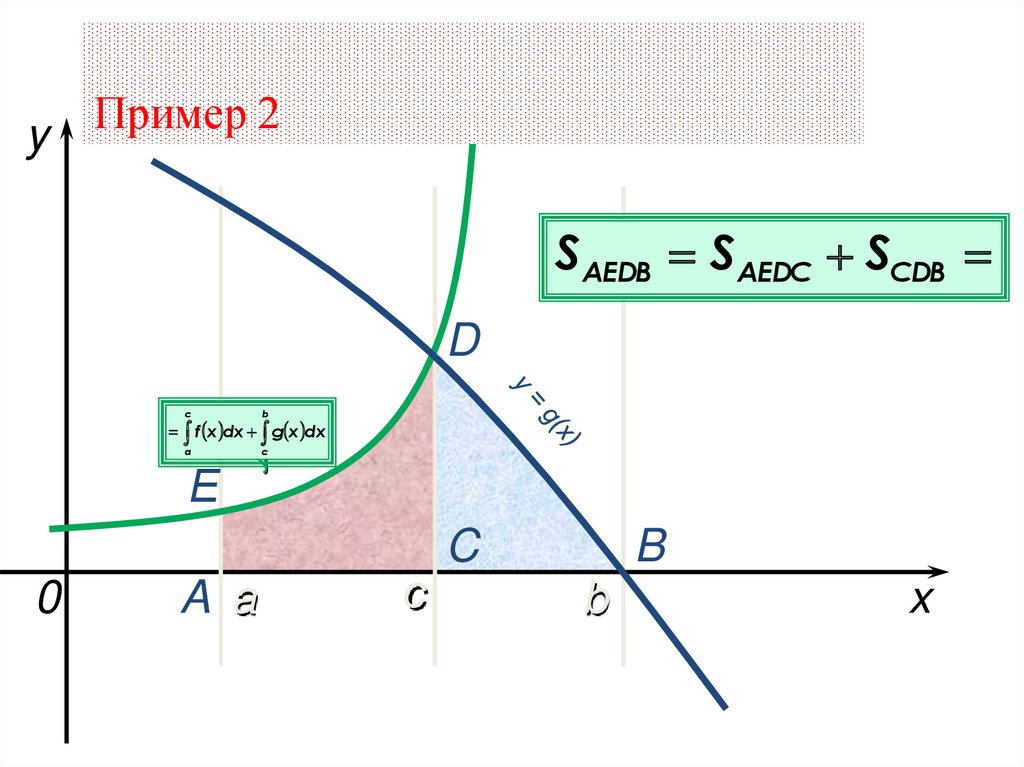
Пример
2
y
SАЕDВ SAEDC SСDB
D
с
b
a
с
f x dx g x dx
Е
0
A a
с
C
B
b
x

8.

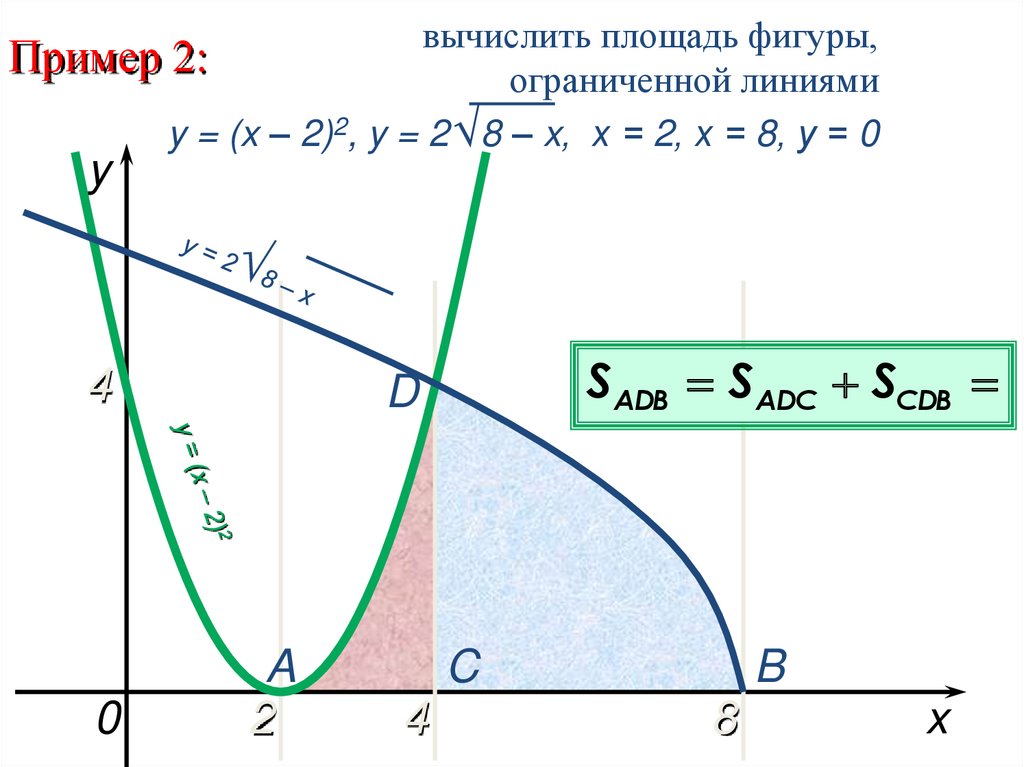
вычислить площадь фигуры,
Пример 2:
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
y
4
0
SАDВ SADС SСDB
D
A
2
C
4
B
8
x

9.

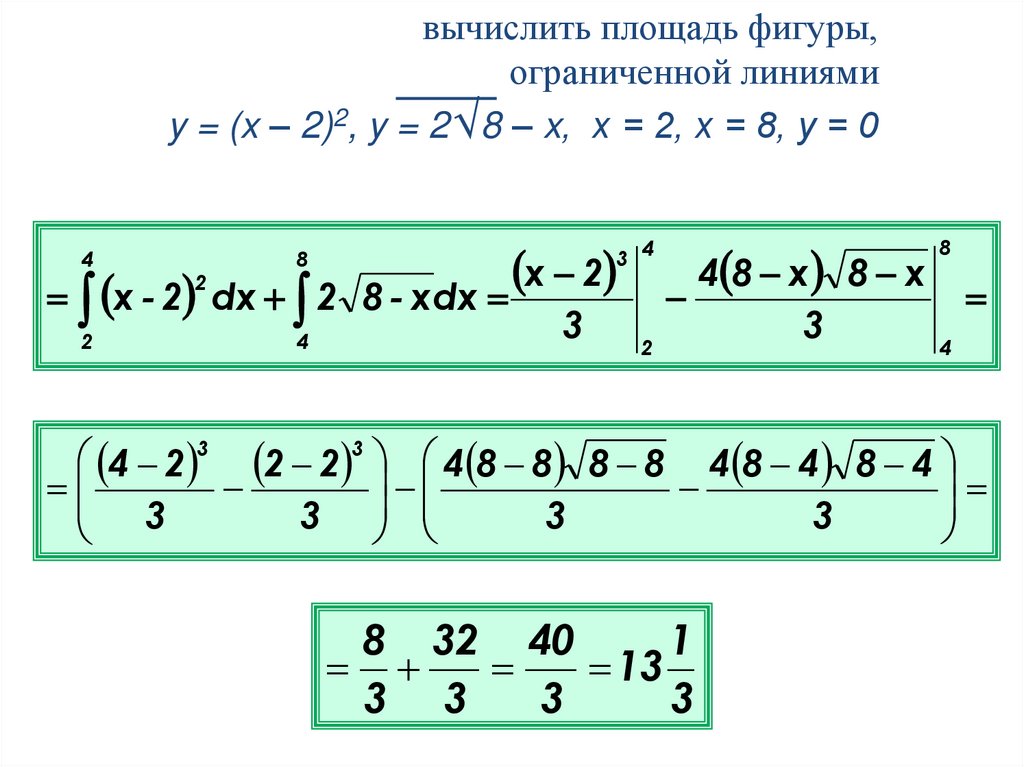
вычислить площадь фигуры,
ограниченной линиями
y = (x – 2)2, y = 2 √ 8 – x, х = 2, х = 8, у = 0
4
8
x - 2 dx 2
2
2
4
3 4
x 2
8 - хdx
3
2
4 8 x 8 x
3
8
4
4 2 3 2 2 3 4 8 8 8 8 4 8 4 8 4
3
3
3
3
8 32 40
1
13
3 3
3
3

10.

11.

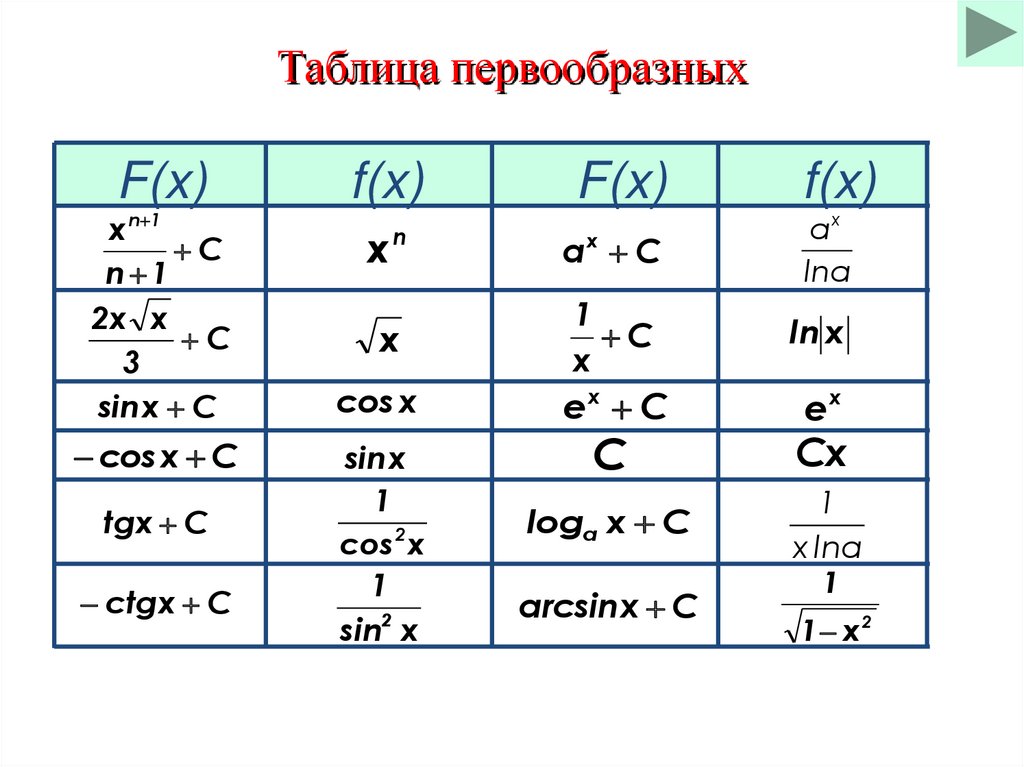
Таблица первообразных
F(x)
x n 1
C
n 1
2x x
C
3
sin x C
cos x C
tgx C
ctgx C
f(x)
f(x)
F(x)
xn
ax C
ax
lna
х
1
C
x
ln x
ex C
ex
cos x
sin x
1
сos 2 x
1
sin2 x
C
Cx
loga x C
1
x lna
arcsin x C
1
1 x2

12.

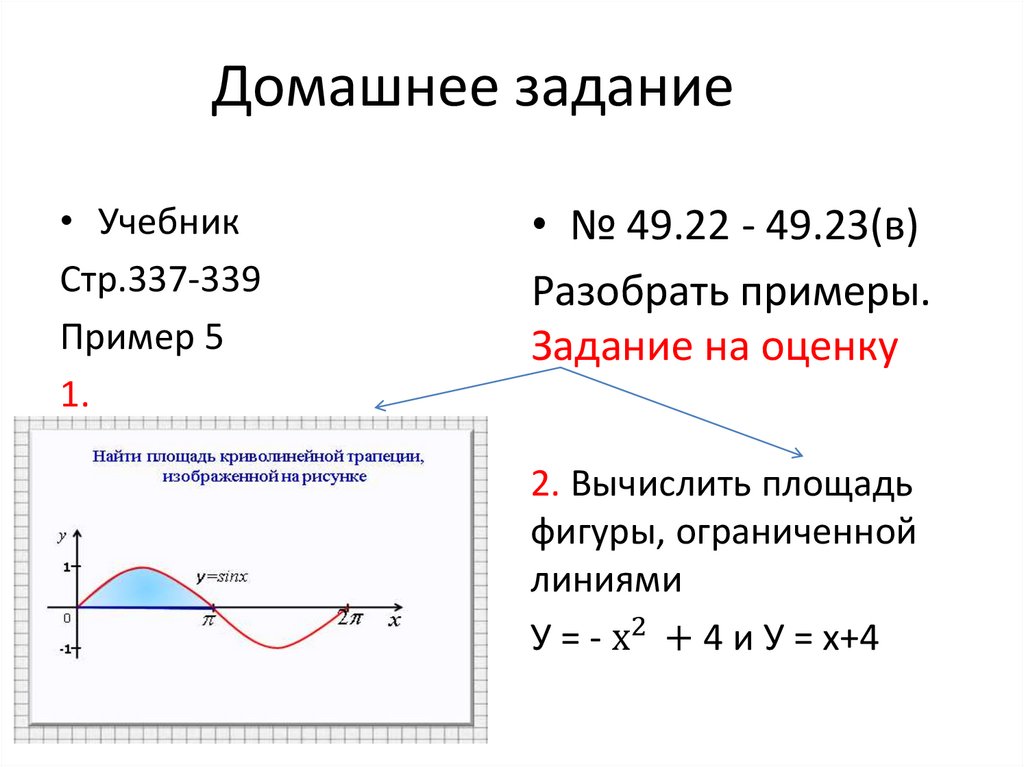
Домашнее задание
• Учебник
Стр.337-339
Пример 5
1.
• № 49.22 - 49.23(в)
Разобрать примеры.
Задание на оценку
2. Вычислить площадь
фигуры, ограниченной
линиями
У = - х2 + 4 и У = х+4