Similar presentations:
Связь математики с другими науками
1.
Связь математики сдругими науками
Выполнила: ученица 9 класса
МКОУ СОШ№5 им.С.К.Магометова
Болатчиева А.И.
Научный руководитель: Узденова С.Д.
2.
• Математика — царица наук». Это изречение, написанноенад школьной доской в кабинете математики, утверждает
превосходство всевозможных формул и цифр. А всегда ли
так было? Или это произошло после какого-то
определенного периода? Я поставила перед
собою цель доказать утверждение о том, что «Математика
– царица всех наук» и на все времена».
3.
• Данный проект актуален, так как он формирует уучащихся представление о математике как о науке
полезной для изучения других предметов, совершенствует
развития интеллектуальных способностей, расширяет
кругозор учащихся.
• Практическая значимость проекта заключается в том,
что его материалы могут быть использованы как на уроках
математики, так и на других уроках, как дополнительный
материал, при подготовке учащихся к олимпиадам и
конкурсам.
• Научность работы определяется тем, что я рассматриваю
следующую гипотезу:
• Математика – первая из всех наук и полезна, и необходима
для них. ( Р. Бэкон)
4.
Великий Карл Гаусс в 18 векесказал:
«Математика – царица всех наук,
а арифметика – царица
математики».
В настоящее время нет предмета
арифметика, есть просто
математика с 1 по 6 класс.
Ещё в 1703 году Леонтий
Магницкий издал первый
русский учебник «Арифметика –
сиречь наука числительная». На
крышке учебника он изобразил
храм наук. На троне – царица
Математика, колонны храма –
прикладные науки: астрономия,
алгебра, физика, геология,
геометрия, тригонометрия,
география, а арифметика – это
начальные ступени всего храма:
сложение, вычитание, деление,
умножение.
5.
6.
Математика – первая из всех наук и полезна, инеобходима для них. (Роджер Бэкон)
Математика в литературе
«Есть кадамба-цветок.
На один лепесток
Пчелок пятая часть опустилась.
Рядом тут же росла
Пусть всего собралось Х
Вся в цвету сименгда,
пчелок, тогда имеем
И на ней третья часть поместилась.
уравнение:
Разность их ты найди,
Ее трижды сложи,
На кутай этих пчел посади.
Лишь одна не нашла
Себе места нигде,
Решив это уравнение,
Все летала то взад, то вперед и везде
получим ответ: 15 пчел.
Ароматом цветом наслаждалась.
Назови теперь мне, подсчитавши в уме,
Сколько пчелок всего здесь собралось?»
7.
Тесная связь архитектуры и математики известна давно. В Древней Греции – геометриясчиталась одним из разделов архитектуры. Современный архитектор должен быть
знаком с различными соотношениями ритмических рядов, позволяющих сделать объект
наиболее гармоничным и выразительным. Кроме того, он должен знать аналитическую
геометрию и математический анализ, основы высшей алгебры и теории матриц, владеть
методами математического моделирования и оптимизации. Не случайно при подготовке
архитекторов за рубежом большое внимание уделяется математической подготовке и
владению компьютером
8.
9.
Самым прочным архитектурным сооружением с давних времен считаютсяегипетские пирамиды. Как известно они имеют форму правильных
четырехугольных пирамид.
Именно эта геометрическая форма обеспечивает наибольшую устойчивость за счет
большой площади основания. С другой стороны, форма пирамиды обеспечивает
уменьшение массы по мере увеличения высоты над землей. Именно эти два
свойства делают пирамиду устойчивой, а значит и прочной в условиях земного
тяготения.
10.
11.
Кроме дольмена, до нас дошло еще одно сооружение, представляющее простейшую стоечнобалочную конструкцию – кромлех. Это также культовое сооружение, предположительно
предназначенное для жертвоприношений и ритуальных торжеств. Кромлех состоял из
отдельно стоящих камней, которые накрывались горизонтальными камнями. При этом они
образовывали две или несколько концентрических окружностей.
Самый знаменитый кромлех сохранился до наших дней в местечке Стоунхендж в Англии.
Некоторые ученые считают, что он был древней астрономической обсерваторией.
12.
13.
Симметричные объекты обладают высокой степенью целесообразности – ведьсимметричные предметы обладают большей устойчивостью и равной
функциональностью в разных направлениях. Все это привело человека к
мысли, что чтобы сооружение было красивым оно должно быть симметричным.
14.
15.
Диссимметрия – это частичное отсутствие симметрии, расстройство симметрии,выраженное в наличии одних симметричных свойств и отсутствии других. Примером
диссимметрии в архитектурном сооружении может служить Екатерининский
дворец в Царском
селе под СанктПетербургом.
Практически в нем
полностью
выдержаны все
свойства симметрии
за исключением
одной детали.
Наличие Дворцовой
церкви расстраивает
симметрию здания в
целом. Если же не
принимать во
внимание эту
церковь, то Дворец
становится
симметричным.
16.
– гармоническая пропорция, это такое пропорциональное деление отрезка нанеравные части, при котором весь отрезок так относится к большей части, как сама
большая часть относится к меньшей; или другими словами, меньший отрезок так
относится к большему, как больший ко всему a : b= b : c или с : b= b : а.
17.
По проекту М. Казакова в Москве была построена Голицынская больница,которая в настоящее время называется Первой клинической больницей имени
Н.И. Пирогова.
Еще один архитектурный шедевр Москвы – дом Пашкова – является одним из
наиболее совершенных произведений архитектуры В. Баженова.
Прекрасное творение В. Баженова прочно вошло в ансамбль центра
современной Москвы, обогатило его. Наружный вид дома сохранился почти без
изменений до наших дней, несмотря на то, что он сильно обгорел в 1812 г.
18.
19.
Изучение внешнего строения человека. Изображениеголовы человека с помощью циркуля и линейки
Построение.
1.Чертим окружность произвольного радиуса.
2.Проводим вертикальный диаметр, выходящий
за пределы окружности, который делим на 3
равные части. Чертим хорды АN и KL,
касательную ST через точки F,O,P
перпендикулярно к диаметру.
3.Из точки касания P проводим вторую
пересекающую окружность, радиус которой
равен 1/3 диаметра большой окружности .
4. Проводим горизонтальный диаметр малой окружности ST и параллельно ей хорду
CM, делящую радиус PB пополам.
5. Верхний сегмент большой окружности показывает границу волос, хорда KL – глаза, в
место касания большой окружности с диаметром малой – ноздри.
6.Соединяем слева и справа две окружности касательными. В точках касания будут
уши.
20.
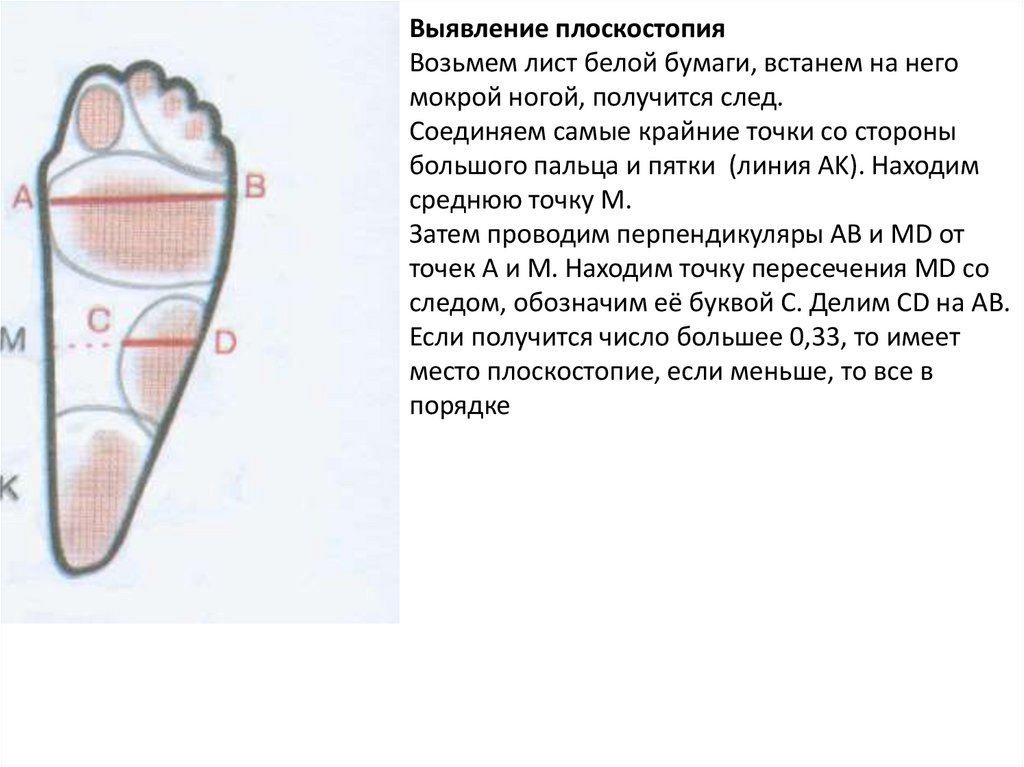
Выявление плоскостопияВозьмем лист белой бумаги, встанем на него
мокрой ногой, получится след.
Соединяем самые крайние точки со стороны
большого пальца и пятки (линия AK). Находим
среднюю точку M.
Затем проводим перпендикуляры AB и MD от
точек A и M. Находим точку пересечения MD со
следом, обозначим её буквой C. Делим CD на AB.
Если получится число большее 0,33, то имеет
место плоскостопие, если меньше, то все в
порядке
21.
22.
С помощью применения математического моделирования разрешаются такие вопросы, как:
1. систематизация полученной информации;
2. оценка рельефных особенностей местности;
3. постройка ГИС;
4. автоматическое зонирование, картирование и классификация;
5. управление и прогнозирование явлений с географической точки зрения;
6. оценка антропогенного воздействия на экосистемы;
Если рассматривать физическую географию, то особое место отведено граф
ическим и математическим моделям. Чаще всего методы математического
анализа встречаются в экономической географии. Спектр использования ма
тематики именно в экономической географии шире, нежели в физической.
Копия горы Маттерхорна (высота
образа 25 нм) —
Альпийская гора с высотой 4478
м, с масштабом 1:5*109
23.
Каким для вас является урок математики?Предмет, который
необходим для
изучения других
предметов
20
20
60
не вижу смысла в
изучении правил и
формул
Сложный, но
интересный,
познавательный
предмет
Из результатов опроса стало видно, что большая часть учащихся
считает, что математика необходима для изучения других предметов
24.
Математика нужна всем людям на земле. Математика нужна вистории, физике, химии, биологии, географии и даже в русском
языке. Математика нужна в повседневной жизни: например, при
кройке шитья, приготовлении пищи или при решении денежных
вопросов. Математика позволяет человеку думать, логически
мыслить, делать выводы.
Проведя исследования, я нашла подтверждения своей гипотезе. И
теперь я могу с твердой уверенностью сказать: «Математика –
царица всех наук». Так было, так есть и так будет.
























 mathematics
mathematics








