Similar presentations:
Связь математики с другими школьными предметами (математика и физика)
1.
Измерение величинНоминация «Связь математики с другими школьными предметами
(математика и физика)»
Выполнил:
ученик 7 класса
МОУ «СОШ п.Белоглинный»
С.А.
Руководитель: учитель
математики Коковина В.П.
2018 год
2.
« Ни одна из естественных наук,если дело идёт не о собирании
материала, а о действительном
творчестве, не обойдётся без
математики – матери всех наук.
Что
же
касается
физики,
поставленной
впереди
всех
других наук… то в настоящее
время математика и физика до
такой степени слились в одно
целое,
что
иногда
трудно
отделить – где кончается физика
и начинается математика».
В.А. Стеклов
3.
Актуальность: знания математикинеобходимы в повседневной жизни
и
физики
Цель: показать взаимосвязь изучаемого материала в
математике и физике
Задачи:
Изучить
дополнительные
информационные
источники по рассматриваемой теме;
Показать какие понятия математики и каким
образом используются в физике;
Рассмотреть
использование
полученных
в
математике знаний для решения физических
задач;
В ходе исследования рассчитать величины: путь,
скорость, объем, плотность, площадь.
4.
ОГЛАВЛЕНИЕВведение
- Связь математики и физики
- Результаты анкетирования
Что значит измерить величину
Метрология
Меры длины на Руси
Практическая работа «Рост учеников 7 класса в
современных и старинных мерах длины»
Практическая работа «Расчет скорости движения»
Практическая работа «Расчет объема и плотности
тела человека»
Практическая работа «Расчет площади фигуры»
Практическая работа «Вычисление значения числа
π»
Погрешность измерений
Заключение
5.
Математика и физикаМатематика и физика встречаются и используются в
повседневной жизни. Нам приходится в жизни считать, мы
постоянно используем (часто не замечая этого) знания о
величинах, характеризующих протяженность, площадь,
объём, промежуток времени, скорость, температуру,
давление и многое другое. Но всё чаще от некоторых своих
одноклассников я слышу вопрос - а так ли уж важно учить
физику и математику? Считать, вроде бы, научились. Может
этого достаточно?
Физик не может не знать
математический язык потому,
что на этом языке написана книга природы, которую
суждено ему читать. Физик не может рассуждать иначе,
как только математически, потому, что он претендует на
точность.
6.
Результаты анкетированияПриняли участие в анкетировании:
14 человек
Нужно ли изучать физику и
математику?
Да – 14
• Нужны ли знания этих предметов
в повседневной жизни?
Да – 11
Не очень, но лучше знать – 1
Не всегда - 2
7.
«Науканачинается с тех пор,
как начинают
измерять.
Точная наука
немыслима без меры»
Д.И.Менделеев
8.
Измерить величину это значит сравнить еёс однородной величиной,
принятой за единицу измерения.
www.fizika.ru
www.fizika.ru
9.
МетрологияМетрология — наука об измерениях, методах и
средствах обеспечения их единства и способах
достижения требуемой точности. Предметом
метрологии является извлечение количественной
информации о свойствах объектов с заданной
точностью и достоверностью; нормативная база для
этого — метрологические стандарты.
10.
История метрологииСерьезным моментом в развитии метрологии, стало
заключение в 1875 году Метрической конвенции и
учреждение Международного бюро мер и весов.
XVIII век — установление эталона метра (эталон хранится
во Франции, в Музее мер и весов; в настоящее время является
в большей степени историческим экспонатом, нежели
научным инструментом);
1832 год — создание Карлом Гауссом абсолютных систем
единиц;
1875 год — подписание международной Метрической
конвенции;
1960 год — разработка и установление Международной
системы единиц (СИ)
11.
История развития метрологиив России
В 1841 году в соответствии с принятым Указом "О
системе Российских мер и весов", узаконившим ряд
мер длины, объема и веса, при Петербургском
монетном дворе было организовано Депо образцовых
мер и весов.
Важным этапом в развитии русской метрологии
явилось подписание Россией метрической
конвенции 20 мая 1875г.
1893 год — создание Д. И. Менделеевым Главной
палаты мер и весов (современное название:
«Научно-исследовательский институт метрологии
им. Менделеева»)
12.
Современные единицы измерения длинызнакомы нам с начала обучения в школе - это
миллиметр, сантиметр, метр, километр,
тонна, килограмм, грамм и другие. Мы
пользуемся ими на уроках и в повседневной
жизни. Не задумываясь, производим
различные вычисления. Они удобны и
понятны. На уроках математики мы
используем для измерения линейку, с
помощью мер длины записываем
результаты в тетрадь. А что же существовало
до того, как изобрели линейку, сантиметр,
метр?
13.
Меры длины на Руси:Вершок 4,4 см
Косая сажень
в плечах.
Семи пядей
во лбу…
Аршин 71 см
От горшка
два вершка.
Каждый купец
на свой
аршин меряет…
14.
Практическая работа:«Рост учеников 7 класса
в современных и старинных
мерах длины»
Современная система
Старинная система
1
174 см
2 аршина 7 вершков ¼ дюйма
2
161 см
2 аршина 4 вершка 1/3 дюйма
3
161 см
2 аршина 4 вершка 1/3 дюйма
4
149 см
2 аршина 1 вершок 1 дюйм
5
152 см
2 аршина 2 вершка ½ дюйма
6
152 см
2 аршина 2 вершка ½ дюйма
7
165 см
2 аршина 5 вершков ¼ дюйма
15.
Роль математики в физике сложнопереоценить. Известна цитата Галилео
Галилея «Математика — это язык, на
котором написана книга Природы». Но
только ли языком является современная
математика? В математике довольно
много встречается задач на расчет
пройденного пути, скорости, объема,
площади
16.
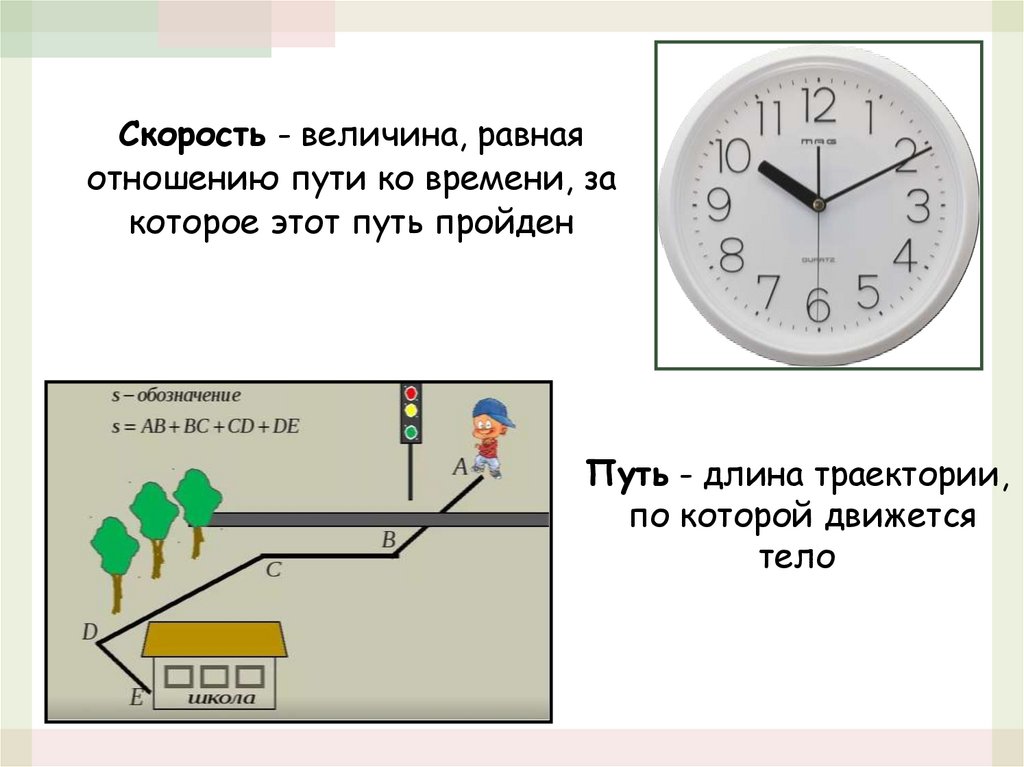
Скорость - величина, равнаяотношению пути ко времени, за
которое этот путь пройден
Путь - длина траектории,
по которой движется
тело
17.
Практическая работа:«Расчет скорости движения»
Средняя
длина
шага
Число
шагов
0,47 м 506
Пройденный
путь
Время
237,82 м 479 с
Скорость
Путь/время
0,5 м/с
18.
Практическая работа:«Расчет объема и плотности тела человека»
Плотность – величина,
равная отношению
массы тела к его объему
Объем - количественная
характеристика
пространства, занимаемая
телом или веществом.
Математическая
модель
тела человека
19.
Объемголовы
(объем
шара)
Объем
туловища
(объем
прямоугол
ьного
параллеле
пипеда)
Объем рук
(объем
прямоугол
ьного
параллеле
пипеда)
Объем ног
(объем
прямоугол
ьного
параллеле
пипеда)
Объем
ступни
(объем
прямоугол
ьного
параллеле
пипеда)
С = 53 см
(обхват
головы)
а=32 см
а=6 см
а=11 см
а=25 см
R=C/6,28=
8,44 см
b=13 cм
b=9 cм
b=11 cм
b=8 cм
с =45 см
с =62 см
с =81 см
с =7 см
V=4/3*3,14
*R3 =
=2517см3
=0,0025м3
V=32*13*45 V=6*9*62*2
=18720 см3 = 6696 см3
=0,01872 м3 =0,0067 м3
V=11*11*81 V=25*8*7*2
*2=19602
=2800 см3
см3
=0,0028 м3
=0,019602
м3
Объем
тела
V=0,050322
м3
20.
Масса – 43 кгОбъем - 0,050322м3
Плотность
43 кг/0,050322м3=854 кг/м3
21.
А как на Руси измеряли массу? Объёмы?22.
Практическая работа:«Расчет площади фигуры»
Площадь - численная характеристика
двумерной геометрической фигуры.
Задание. Определите площадь фигуры, вырезанной
из картона
Оборудование:
электронные весы, картон,
полоска бумаги шириной 1 см,
ножницы.
23.
Масса фигуры М пропорциональна ее площади(картон одинаков по толщине). С помощью
полоски бумаги как «мерной единицы»
начертил
на
фигуре
прямоугольник
с
известными
сторонами,
вырезал
его
и
определил массу этого прямоугольника.
Масса фигуры 10 г, масса прямоугольника 5 г.
Площадь всей фигуры S во столько раз больше
площади прямоугольника s, во сколько раз
масса всей фигуры М больше массы m
прямоугольника S: s = М: m.
S:294,5=10:5
S= 589 см2
24.
Что мы знаем о числе «Пи»?Число Пи –
математическая
константа, выражающая
отношение длины
окружности к длине ее
диаметра
25.
Практическая работа:«Вычисление значения числа
Задание:
Вырежьте из одинаковой бумаги круг и
квадрат со стороной, равной радиусу круга.
Взвесив обе фигуры, используя
геометрические и физические знания, найдите
значение числа π.
Оборудование:
электронные весы, листы
бумаги, измерительная линейка,
циркуль, ножницы.
π»
26.
Масса круга М = 5 г, масса квадрата 1,6 г. Площадькруга S во столько раз больше площади квадрата s, во
сколько раз масса круга М больше массы m квадрата S: s
= М: m.
Площадь круга вычисляется по формуле S = πR2.
Площадь квадрата s= R2 .
πR2 : R2 = 5 : 1,6
π = 3,125
27.
Погрешность:-неточность, ошибка в измерениях.
Погрешность измерения
не может быть больше
цены деления шкалы
измерительного
прибора
Погрешность
измерений равна цене
деления шкалы
измерительного
прибора или половине
цены деления
∆=½с
28.
ЗаключениеЗначение математики для физики очень огромно.
Математика предопределяет большинство законов
природы. Она является специальным языком,
помогающим исследовать не только окружающий нас
мир, но и целую Вселенную. Математика, как
фундаментальная наука, является системой
различных методов, которые помогают развитию
естественных наук в различных направлениях.
Применение математики в физике и естественных
науках очень огромно, в каждой науке есть хоть одна
частица применения математики.
29.
Использованные источникиПерышкин А.В. Физика 7 класс М.: «Дрофа», 2016.- 224с.
http://interesnyjfakt.ru/kak-ranshe-opredelyali-vremya/
http://rus-ved-rus.narod.ru/mery.html
http://www.class-fizika.narod.ru/
http: //www.habit.ru/35/179
https://ru.wikipedia.org/wiki/%D0%9F%D0%BB%D0%BE%D1%8
2%D0%BD%D0%BE%D1%81%D1%82%D1%8C
http://fb.ru/article/225613/starinnyie-meryi-izmereniyadlinyi-ploschadi-massyi-znachenie-starinnyih-mer-izmereniyavelichin-na-rusi
https://fs00.infourok.ru/images/doc/127/148359/img7.jpg
http://tambov.xn----itbkcijdbf2ab0f9b.xn-p1ai/upload/iblock/b21/b21a457e88edff444bfc8cf626bc3c2d.
jpeg
https://studfiles.net/preview/634735/page:18/




























 mathematics
mathematics physics
physics








