Similar presentations:
Экспериментальные и теоретические основы квантовой теории
1. Экспериментальные и теоретические основы квантовой теории.
Государственный университет «Дубна»Инженерно-физический институт
Кафедра ядерной физики
Кафедра фундаментальных проблем физики микромира
Специальный семинар по физике ядра и ядерным реакциям
В.В.Самарин
Экспериментальные и
теоретические основы
квантовой теории.
Вопросы 1, 2, 3, 4, 5, 6.
2020
1
2. Вопрос 1
Экспериментальные факты, лежащие
в основе квантовой теории.
1. Излучение абсолютно черного тела,
фотоэффект и эффект Комптона.
2. Спектры атомов водорода и щелочных
элементов.
Атом водорода по Бору.
Волновые и корпускулярные свойства
материи.
2
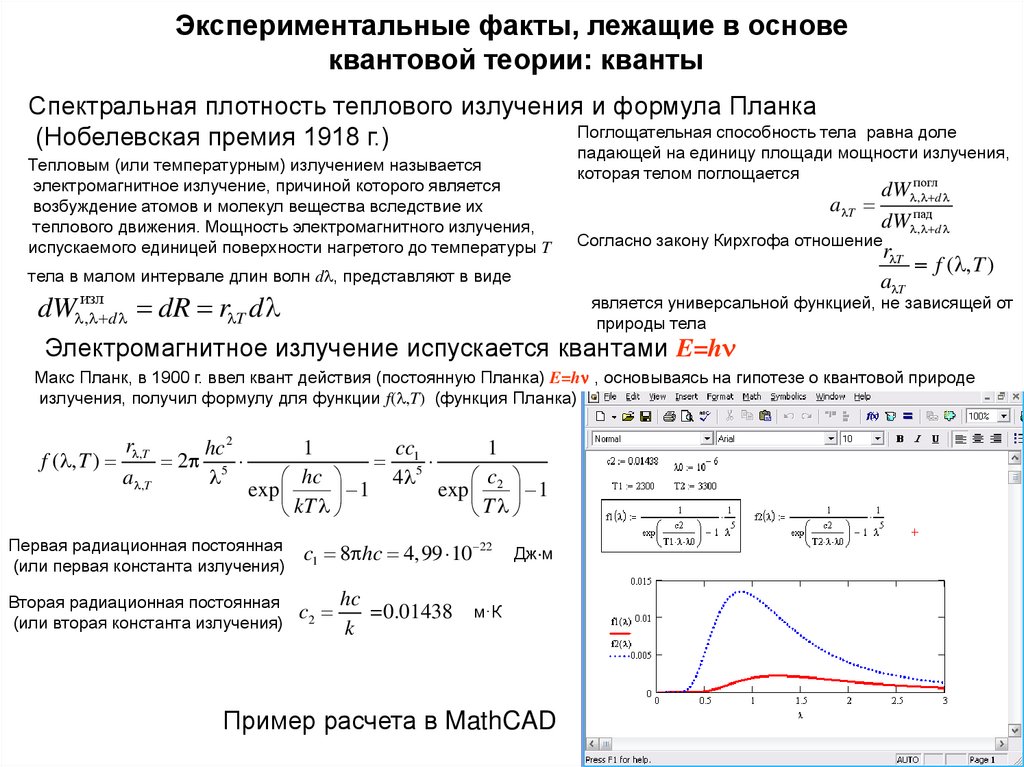
3. Экспериментальные факты, лежащие в основе квантовой теории: кванты
Спектральная плотность теплового излучения и формула ПланкаПоглощательная способность тела
(Нобелевская премия 1918 г.)
Тепловым (или температурным) излучением называется
электромагнитное излучение, причиной которого является
возбуждение атомов и молекул вещества вследствие их
теплового движения. Мощность электромагнитного излучения,
испускаемого единицей поверхности нагретого до температуры T
тела в малом интервале длин волн d , представляют в виде
изл
, d
T
dW
dR r d
равна доле
падающей на единицу площади мощности излучения,
которая телом поглощается
погл
a T
dW , d
dW пад
, d
Согласно закону Кирхгофа отношение
r T
f ( , T )
a T
является универсальной функцией, не зависящей от
природы тела
Электромагнитное излучение испускается квантами E=hn
Макс Планк, в 1900 г. ввел квант действия (постоянную Планка) E=hn , основываясь на гипотезе о квантовой природе
излучения, получил формулу для функции f( ,T) (функция Планка)
f ( , T )
r ,T
a ,T
hc 2
2 5
1
cc
1
15
4
hc
c2
exp
1
exp
1
kT
T
Первая радиационная постоянная
(или первая константа излучения)
c1 8 hc 4,99 10 22
Вторая радиационная постоянная
(или вторая константа излучения)
c2
Дж м
hc
=0.01438 м·К
k
Пример расчета в MathCAD
3
4. Экспериментальные факты, лежащие в основе квантовой теории: фотоны
Внешний фотоэффект - излучение поглощается квантами E=hnФотоэффектом называется испускание электронов веществом при поглощении им квантов электромагнитного излучения
(фотонов). Фотоэффект был открыт в 1887 г. Г.Герцем, который обнаружил, что искровой разряд между двумя
электродами происходит при меньшем напряжении, если искровой промежуток освещается светом с большой долей
ультрафиолетового излучения. Первые исследования фотоэффекта выполнены А.Г.Столетовым (1888 г.),
Ф.Ленардом и Дж. Дж. Томсоном (1889 г.). Основные закономерности фотоэффекта были объяснены в 1905 г.
А.Эйнштейном на основе представлений о поглощении энергии электромагнитного поля квантами.
Нобелевская премия по физике (1921 г.).
hn Aвых
mv 2max
2
Эффект Комптона - фотоны имеют энергию и импульс
Нобелевская премия 1925
h
h
0
Схема опыта Комптона
mc
1 cos 2
mc
sin 2
2
Спектры рассеянного рентгеновского излучения
Исходящее из рентгеновской трубки 1 монохроматическое (называемое характеристическим) рентгеновское излучение
с длиной волны λ0, проходит через свинцовые диафрагмы 2 и в виде узкого пучка направляется на рассеивающее вещество
– мишень 3. Излучение, рассеянное под некоторым углом θ, анализируется с помощью спектрографа рентгеновских лучей 4,
в котором роль дифракционной решетки играет кристалл 5, закрепленный на поворотном столике.
4
5. Таблицы физических величин
56. Экспериментальные факты, лежащие в основе квантовой теории: спектры атомов водорода, щелочных элементов и ртути
1. Серия Бальмера в спектре атома Н.2. Линейчатые спектры атомов Na и Hg.
Спектр
излучения Na
Спектр Hg
Спектр
поглощения Na
Спектры излучения атомов H, Hg и молекулы Н2
Hg
Частоты линий равны разностям термов
n T (n1 ) T (n2 ), T (n1 ) 0, T (n2 ) 0
Формула Бальмера для длин волн
в видимой и ближней ультрафиолетовой
частях спектра, RH -постоянная Ридберга
1 1
1 n
RH 2 2 , n2 n1 1, n1 2,
c
n1 n2
, n1 2
Спектральные серии атома натрия,
границы серий показаны штриховкой;
Длины волн главной серии натрия
1
1
1
, n 3, 4,5,
R
3 s 2 n 2
n ,P
p
s , p – квантовые дефекты
6
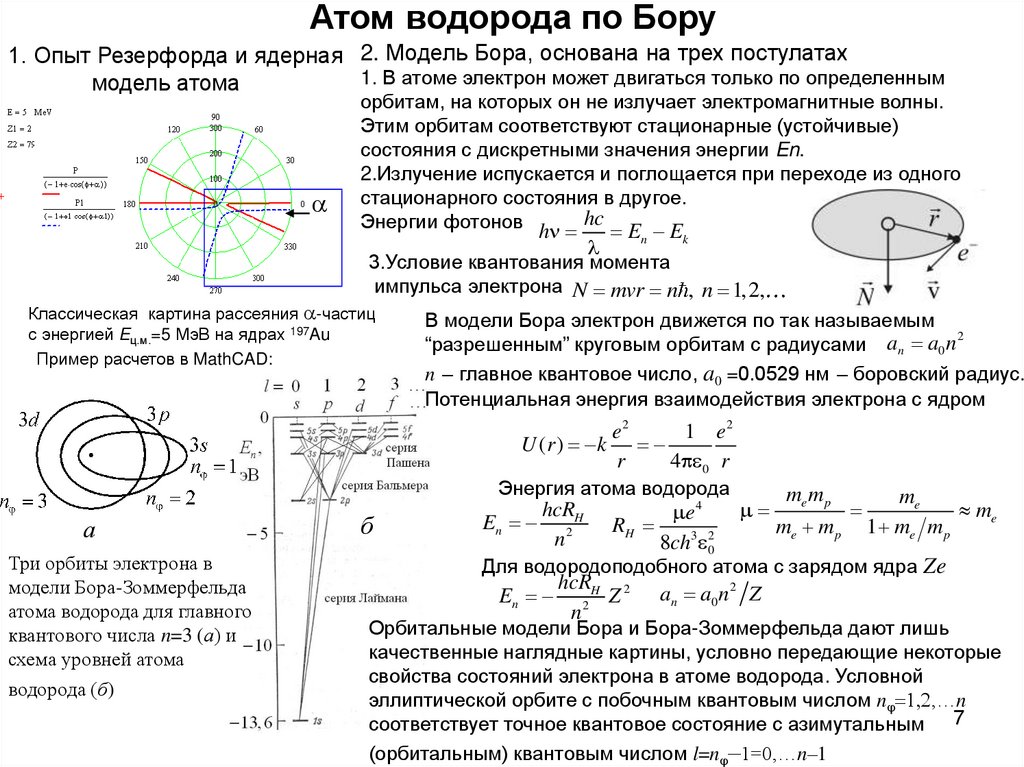
7. Атом водорода по Бору
1. Опыт Резерфорда и ядерная 2. Модель Бора, основана на трех постулатах1. В атоме электрон может двигаться только по определенным
модель атома
a
орбитам, на которых он не излучает электромагнитные волны.
Этим орбитам соответствуют стационарные (устойчивые)
состояния с дискретными значения энергии En.
2.Излучение испускается и поглощается при переходе из одного
стационарного состояния в другое.
Энергии фотонов hn hc E E
n
k
3.Условие квантования момента
импульса электрона N mvr n , n 1, 2,
Классическая картина рассеяния a-частиц
с энергией Eц.м.=5 МэВ на ядрах 197Au
Пример расчетов в MathCAD:
В модели Бора электрон движется по так называемым
2
“разрешенным” круговым орбитам с радиусами an a0 n
n – главное квантовое число, a0 =0.0529 нм – боровский радиус.
Потенциальная энергия взаимодействия электрона с ядром
e2
1 e2
U (r ) k
r
4 0 r
Энергия атома водорода
а
Три орбиты электрона в
модели Бора-Зоммерфельда
атома водорода для главного
квантового числа n=3 (а) и
схема уровней атома
водорода (б)
б
hcR
En 2 H
n
e 4
RH
8ch3 02
me m p
me m p
me
me
1 me m p
Для водородоподобного атома с зарядом ядра Ze
hcR
2
En 2 H Z 2 an a0 n Z
n
Орбитальные модели Бора и Бора-Зоммерфельда дают лишь
качественные наглядные картины, условно передающие некоторые
свойства состояний электрона в атоме водорода. Условной
эллиптической орбите с побочным квантовым числом nj 1,2,…n
соответствует точное квантовое состояние с азимутальным 7
(орбитальным) квантовым числом l=nj–1=0,…n–1
8. Экспериментальные факты, лежащие в основе квантовой теории: спектры атомов водорода и щелочных элементов
hnЭнергии фотонов
1. Серия Бальмера в спектре атома Н.
hc
En2 En1 , En2 0, En1 En2 0
2. Линейчатые спектры атома Na.
Спектр
излучения Na
Спектр Hg
Спектр
поглощения Na
Спектры излучения атомов H, Hg и молекулы Н2
n2
Hg
n1
1 1
1
RH 2 2 , n2 n1 1, n1 2,
n1 n2
En,s
E1
n s
En , p
, n1 2
E1 13,6 эВ
, n 3, 4,
2
E1
n
p
2
, n 3, 4,
s , p – ридберговские поправки (или квантовые дефекты
а) Спектральные серии
атома натрия, границы
серий показаны штриховкой;
б) схема уровней атома
натрия переходы между
ними, приводящие к
образованию серий; рядом
d <<1 с переходами указаны
длины волн излучения в нм
En ,d
E1
, n 3, 4,
2
n
8
9. Экспериментальные факты, лежащие в основе квантовой теории: волновые и корпускулярные свойства материи
1. Дифракция электронов:а) при отражении от поверхности
монокристаллов (К. Девиссон)
б) при прохождении через фольгу
(Дж. П. Томсон)
Нобелевская премия 1937.
2. Длина волны де Бройля h
p
Нобелевская премия 1929.
Условие квантования
момента импульса электрона
3. Эффект Рамзауэра
mvr n n
2 r n
h
, n 1, 2,
2
h
n , n 1, 2,
mv
9
10. Пример расчета длины волны де Бройля
[ì ]h
h
h
h[Äæ ñ]
p
2mE
p2
2 Au êã E ýÂ 1.6 10 19 [Äæ ýÂ 1 ]
[ô ì ] 1015
h[Äæ ñ]
2 Au êã E ýÂ 1.6 10 19 [Äæ ýÂ 1 ]
A 16, Ec.m. 70 Ì ýÂ, Elab 75 Ì ýÂ
[ô ì ] 1015 10 34
6.626
2 16 1.66 75 1.6 10 19 10 27 106
6.626
1015 34 20
2 16 1.66 75 1.6
10
11. Вопрос 2
Основные постулаты квантовой
механики.
Чистые и смешанные состояния
квантовомеханической системы.
Волновая функция, матрица
плотности.
Принцип неопределенности
11
12. Основные постулаты квантовой механики.
1.2.
ˆ
Физическим величинам
rˆ r , pˆ x i
, p i , fˆ f r , pˆ
сопоставляются операторы.
x
Энергии сопоставлен оператор
2
Гамильтона (гамильтониан) Н.
Hˆ
U (r ),
2m
Среднее значение физической
величины f при измерении для
некоторого состояния системы
плотность вероятности
равно интегралу
f y* fˆ ydq
2
где y – волновая функция
y
системы. В стационарном
состоянии с yn - собственной
fˆ yn fnyn
функцией оператора при
измерении f получится
собственное значение оператора
fn. Стационарное уравнение
Hˆ yn Enyn
траектории
Шредингера
2
Плотность вероятности равна y
нормировка
y n* y n dq 1
Матрицы операторов
Квантовая (верхняя половина) и классическая
3.
4.
f nm y n* fˆ y m dq
В квазиклассическом пределе
h 0 y aexp(iS/h),
S − действие.
В пределе малых длин волн
де Бройля плотность вероятности
соответствует классическим
траекториям частицы.
(нижняя половина) картины столкновения ядер
16О + 208Pb: для энергии E=70 МэВ,
упругое рассеяние, длина волн де Бройля мала
по сравнению с размерами ядер.
Окружность - точки соприкосновения ядер.
Степень почернения пропорциональна
12
плотности вероятности
13. Операторы
Транспонированный оператор fˆдля оператора fˆ
fˆ dq fˆ dq
Комплексно сопряженный оператор fˆ * для оператора fˆ
Сопряженный оператор
fˆ fˆ * для оператора
fˆ
Собственные и средние значения физических величин вещественны
fˆ dq fˆ dq
*
*
*
* *
fˆ dq fˆ dq fˆ dq,
*
*
Эрмитовы (самосопряженные) операторы
fˆ fˆ * , fˆ fˆ
Операторы, соответствующие в математическом аппарате квантовой
механики вещественным физическим величинам должны быть эрмитовыми
(самосопряженными) .
13
14. Чистые и смешанные состояния
Состояния квантовой системы, описываемые волновой функцией, называются
чистыми состояниями. Они соответствуют максимально полным сведениям о
квантовой системе. В общем случае
волновые функции могут быть
представлены в виде суперпозиции собственных функций некоторых
операторов, имеющих дискретный и непрерывный спектр собственных значений
(принцип суперпозиции).
y an y n aF y F dF
n
Состояния, которым нельзя сопоставить волновую функцию называют
смешанными состояниями.
Примерами могут быть состояния, задаваемые
2
2
an , aF
набором чисел
, т.е. вероятностями состояний с определенными
значениями соответствующих величин F. Смешанное состояние можно
рассматривать как некогерентную смесь чистых состояний y(i) со
статистическими
весами
W(i),
удовлетворяющими
соотношению
W (i) 1
i
При вычислении среднего значения какой-либо физической величины в
смешанном состоянии необходимо определить значения этой величины в
чистых состояниях y(i) и усреднить полученные величины со статистическими
весами W(i):
F W (i ) y*(i ) Fˆ y (i ) d
i
Для вычисления средних значений и вероятностей различных значений физических
14
величин в смешанных состояниях используется матрица плотности.
15. Матрица плотности
Матрица плотности r может быть определена для состояний поляризацииили других состояний для конечного числа собственных функций некоторого
оператора. Для произвольного чистого состояния
y (i ) an(i ) y n ,
n
a
*( i ) ( i )
n
n
n
a
1, Lnn y*n Lˆy n d , L( i ) y*( i ) Lˆy ( i ) d Lnn an*( i ) an( i ) ,
nn
L W (i ) y*( i ) Lˆ y ( i ) d W (i )L( i ) W (i ) Lnn an*( i ) an( i ) Lnn rn n Lr nn Sp( Lr),
i
i
i
nn
nn
n
rn n W (i )an*( i ) an(i ) , rn n r*nn , Sp(r) 1.
i
Если в квантовой системе возможно N независимых чистых состояний, то N2
комплексных элементов матрицы плотности r зависят от N2 1 действительных
параметров.
В более общем случае матрица плотности характеризует произвольное
состояние подсистемы (с полным набором координат x), образующей
вместе со второй подсистемой (с полным набором координат x) большую
систему с волновой функцией y x,x ,
y(x, x) s (x)js ( x),
s
где js(x) полная ортонормированная система собственных функций некоторого
оператора, действующего на координаты подсистемы x.
L y* (x, x) Lˆx y(x, x)dxd x rss (x) j*s ( x)Lˆx js ( x)dx, r ss (x) *s (x) s (x) d x,
ss
rss (x) матричные элементы матрицы плотности в s-представлении,
матрица плотности как функция координат подсистемы x:
r( x, x ) y* (x, x )y(x, x)d x r ss (x)j*s ( x )j s ( x)
ss
15
16. Принцип неопределенности
Две физические величины не могут иметь одновременно определенные значения ни в одном
состоянии, если их операторы не коммутируют, пример:
Для двух самосопряженных операторов Fˆ ,
( M̂ также самосопряженный оператор)
pˆ x x xpˆ x i
Kˆ с перестановочным соотношением
ˆ ˆ KF
ˆ ˆ iMˆ
FK
1
F K M
2
соотношение неопределенности для величин F и К:
Для координаты и проекции импульса на ту же ось получается соотношение неопределенности
1
Гейзенберга
px x
Ekin
2
Соотношение неопределенности часто используют для оценки среднего значения кинетической
энергии частицы, которая движется в некотором ограниченном объеме пространства с линейным
2
размером а:
1
2m
px
2
8ma 2
В силу малости постоянной Планка соотношение неопределенности существенно только для
микросистем. Согласно Н.Бору каждая физическая величина вместе со своей канонически
сопряженной (например, х и рх) образуют пару дополнительных величин. В любом состоянии
квантовых систем определенное значение может иметь только одна из них, либо обе не имеют
определенного значения. Согласно принципу дополнительности Бора два взаимно исключающих
класса квантового описания состояний могли бы дать при классическом описании полное
описание состояния системы, например, задать начальные условия для определения
единственной траектории материальной точки.
16
17. Вопрос 3
1. Описание эволюцииквантовомеханических систем.
2. Уравнения Гейзенберга и
Шредингера.
3. Стационарные состояния.
17
18. Волновая функция и уравнение Шредингера
Стационарное уравнение ШредингераHˆ y Ey,
2
2m
y
y U (r )y Ey,
2m
2
E U (r ) y 0
Нестационарное уравнение Шредингера выражает принцип причинности в
Оно позволяет определить значение волновой
квантовой механике
функции (t) в любой момент времени t , если
известно это значение в начальный момент t0.
2
ˆ
i
H , i
U (r , t ) ,
t
t
2m
Изменение со временем средних значений физических величин
d
d
* ˆ
* ˆ
* ˆ
f f dq f dq
f dq * fˆ
dq
dt
dt
t
t
t
1
* ˆ
* ˆ ˆ
* ˆˆ
* ˆ
f dq
f
H
dq
Hf
dq
f dq
i
t
Дифференцирование операторов по времени
ˆ fˆ i ˆ ˆ ˆ ˆ
f
Hf fH
t
Пример: оператор производной скорости по времени − оператор ускорения
i ˆ
ˆ
ˆ ˆ U
mv m Hvˆ vH
18
19. Изменение со временем состояний, описываемых матрицей плотности
rn n (t ) W (i)an*(i ) (t )an(i ) (t )i
Дифференцирование с учетом нестационарного уравнения Шредингера
приводит к уравнению в матричных обозначениях (Н – матрица гамильтониана):
r
i
H r rH
t
Это уравнение называют квантовым уравнением Лиувилла, так как оно
соответствует уравнению Лиувилла для классической функции распределения
в статистической физике
19
20. Описание эволюции квантово-механических систем. Уравнения Гейзенберга и Шредингера.
Изменение со временем волновой функции в представлении Шредингераi
ˆ
i ˆ
1 ˆˆ 2
H , (t ) 1
Ht
HHt
2
t
1!
2!
i ˆ
(0) exp Ht (t 0).
Изменение со временем плотности вероятности в представлении Шредингера
*
1
1
*
*
* Hˆ Hˆ * ,
t
t
t
i
i
i ˆ
(0)
exp
H
Ht (t )
Волновая функция в представлении Гейзенберга (Н) не зависит от времени
Операторы в представлении Гейзенберга зависят от времени t: fˆ exp i Ht
ˆ fˆ exp i Ht
ˆ , Hˆ Hˆ
H
H
Средние значения физических величин в представлениях Шредингера
и Гейзенберга (Н)
f * (t ) fˆ (t )dq
*
ˆ
i ˆ
i ˆ
i ˆ ˆ
i ˆ
*
* ˆ
f exp Ht
(0)
f
exp
Ht
(0)
dq
exp
Ht
f
exp
H
Ht H dq H f H H dq
Изменение со временем средних значений физических величин в представлениях Шредингера и
Гейзенберга (Н)
fˆH i
*
* ˆ
* d ˆ
*
ˆ
ˆ
ˆ
ˆ
ˆ
f (t ) f (t )dq H f H H dq H
f H H dq H
Hf H f H H H dq
t
t
t
t
dt
Уравнения для операторов в представлении Гейзенберга
fˆH i ˆ ˆ
d ˆ
fH
Hf H fˆH Hˆ
dt
t
20
21. Плотность потока вероятности
2ˆ
i
H , i
U (r , t ) ,
t
t
2m
d
d
*
*
P dV
dV *
dV
dt
dt
t
t
1
* Hˆ dq Hˆ * * dV
i
1
* Hˆ dq Hˆ *dV divjdV
i
Уравнение непрерывности
r
divj 0
t
Вектор плотности тока вероятности
j
y y y y
2mi
*
*
21
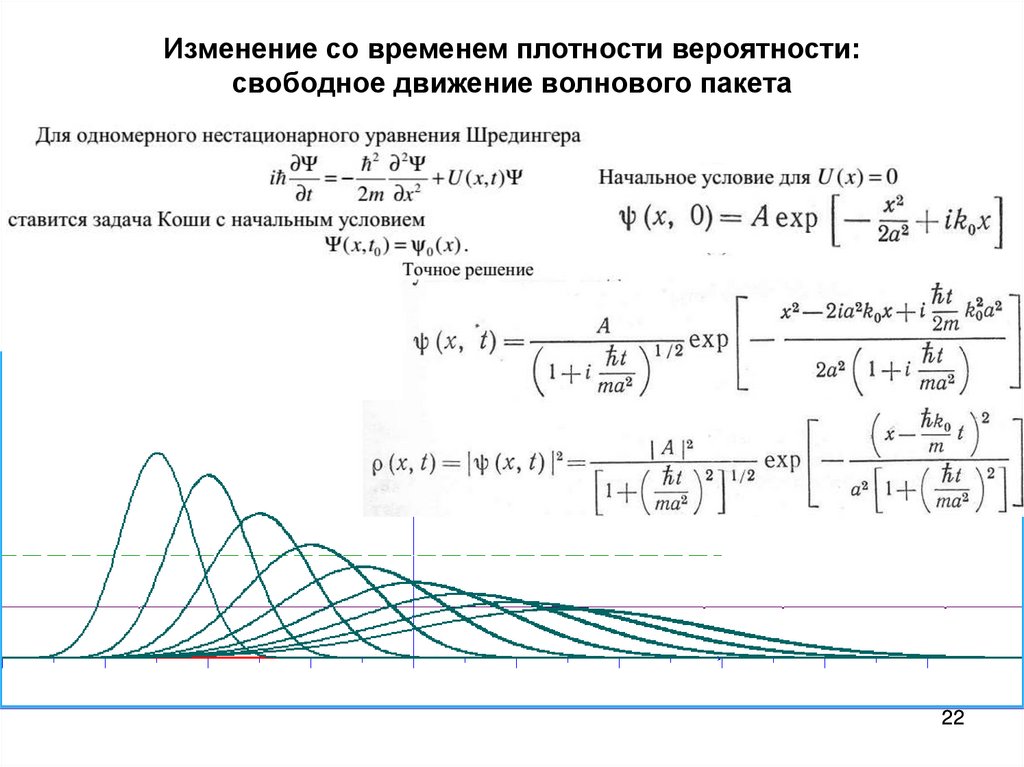
22. Изменение со временем плотности вероятности: свободное движение волнового пакета
2223. Изменение со временем плотности вероятности: столкновение волнового пакета с барьером
2324. Пример изменения со временем плотности вероятности: одномерная модель реакции передачи нейтрона при столкновении атомных ядер
В. В. Самарин ЯДЕРНАЯ ФИЗИКА, 2015, том 78,№1-2, с. 133–14624
25. Стационарные состояния
Состояния, в которых энергия имеет определенные значения (энергетическиеуровни), называются стационарными состояниями системы.
Hˆ y n En y n ,
i
2
2m
y n U (r )y n En y n ,
n
i
Hˆ n En , n exp Ent y n (q)
t
Стационарное состояние с наименьшим из всех возможных значением энергии
называется нормальным или основным состоянием системы.
Разложение произвольной волновой функции по волновым функциям
стационарных состояний с вероятностями an 2 различных значений энергии
системы:
i
an exp Ent y n (q)
n
Уровни энергии, которым соответствуют несколько различных стационарных
состояний называются вырожденными.
Стационарное состояние дискретного спектра всегда соответствует финитному
движению системы, т.е. движению, при котором система или какая-либо ее часть
не уходит на бесконечность система находится в связанном состоянии).
25
Стационарные состояния непрерывного спектра соответствуют
инфинитному движению системы.
26. Вопрос 4
1. Линейный квантовый гармоническийосциллятор.
2. Энергии
и
волновые
функции
стационарных состояний.
26
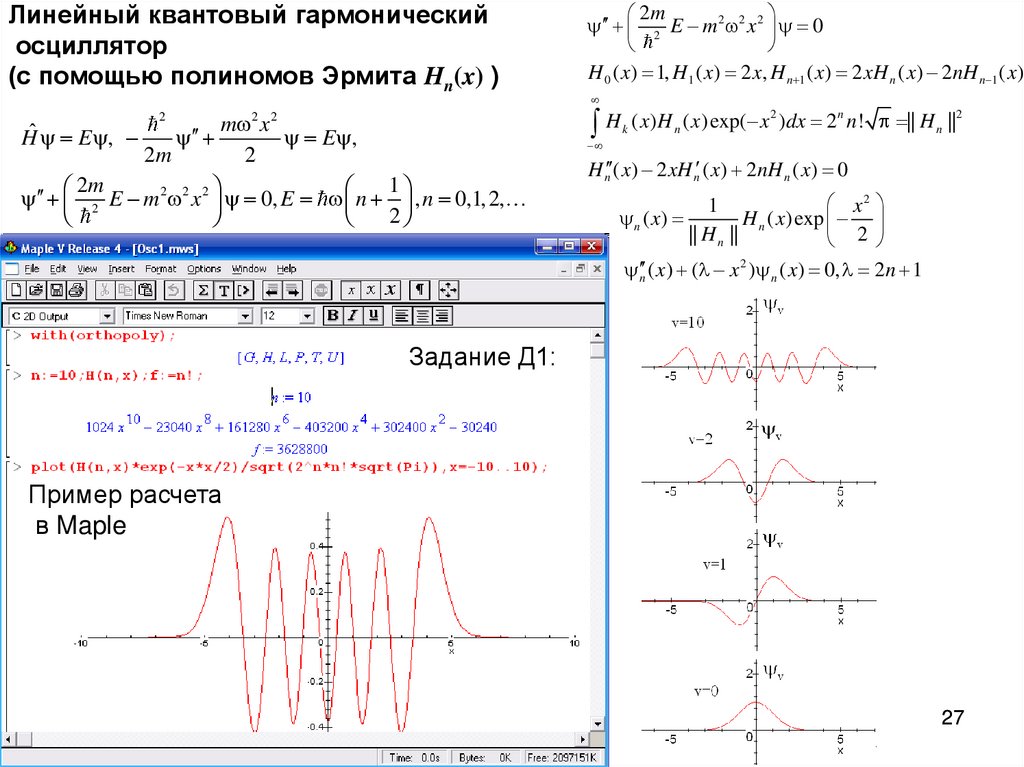
27. Линейный квантовый гармонический осциллятор (с помощью полиномов Эрмита Hn(x) )
m xy
y Ey ,
2m
2
1
2m
y 2 E m 2 2 x 2 y 0, E n , n 0,1, 2,
2
Hˆ y Ey,
2
2
2
2m
y 2 E m 2 2 x 2 y 0
H 0 ( x) 1, H1 ( x) 2 x, H n 1 ( x) 2 xH n ( x) 2nH n 1 ( x)
H
k
( x) H n ( x) exp( x 2 )dx 2n n ! || H n ||2
H n ( x) 2 xH n ( x) 2nH n ( x) 0
x2
1
y n ( x)
H n ( x) exp
|| H n ||
2
y n ( x) ( x 2 )y n ( x) 0, 2n 1
Задание Д1:
Пример расчета
в Maple
27
28. Линейный квантовый гармонический осциллятор (с помощью полиномов Эрмита Hn(x) )
2 2m
x
Hˆ y E y,
y
y Ey,
2m
2
2m
y 2 E m 2 2 x 2 y 0,
1
E n , n 0,1, 2,
2
2
2m
y 2 E m 2 2 x 2 y 0,
y n ( x)
x2
1
m
H n (x) exp , x x
,
|| H n ||
2
H 0 ( x) 1, H1 ( x) 2 x, H n 1 ( x) 2 xH n ( x) 2nH n 1 ( x),
H
k
( x) H n ( x) exp( x 2 )dx 2n n ! || H n ||2 ,
H n ( x) 2 xH n ( x) 2nH n ( x) 0,
y n ( x) ( x 2 )y n ( x) 0, 2n 1,
y n ( x)
x2
1
H n ( x) exp .
|| H n ||
2
Пример расчета в MathCAD
28
29. Линейный квантовый гармонический осциллятор (матричный метод)
ivˆ
m
1
ˆ ˆ U
Hvˆ ˆ vH
m
29
30. Вопрос 5
1. Прохождение частиц черезпотенциальный барьер.
2. Туннельный эффект.
3. Квазиклассическое приближение и
модель параболического барьера.
4. Математическая модель туннельного
эффекта.
30
31. Изменение со временем плотности вероятности: столкновение волнового пакета с барьером
Численное решение нестационарногоуравнения Шредингера
| x,t |2
Прохождение частиц
через потенциальный барьер
U(x)
E
|y x |2
Отражение
|y x |2
U(x)
E
Численное решение стационарного
уравнения Шредингера для
установившегося режима при
непрерывном движении частиц
из - на потенциальный барьер
31
32. Постановка задачи о прохождения частиц через потенциальный барьер
ОтражениеПрохождение
|y x |2
U(x)
E
32
33. Туннельный эффект в устройствах с p-n переходом и резонансное туннелирование в стабилитроне
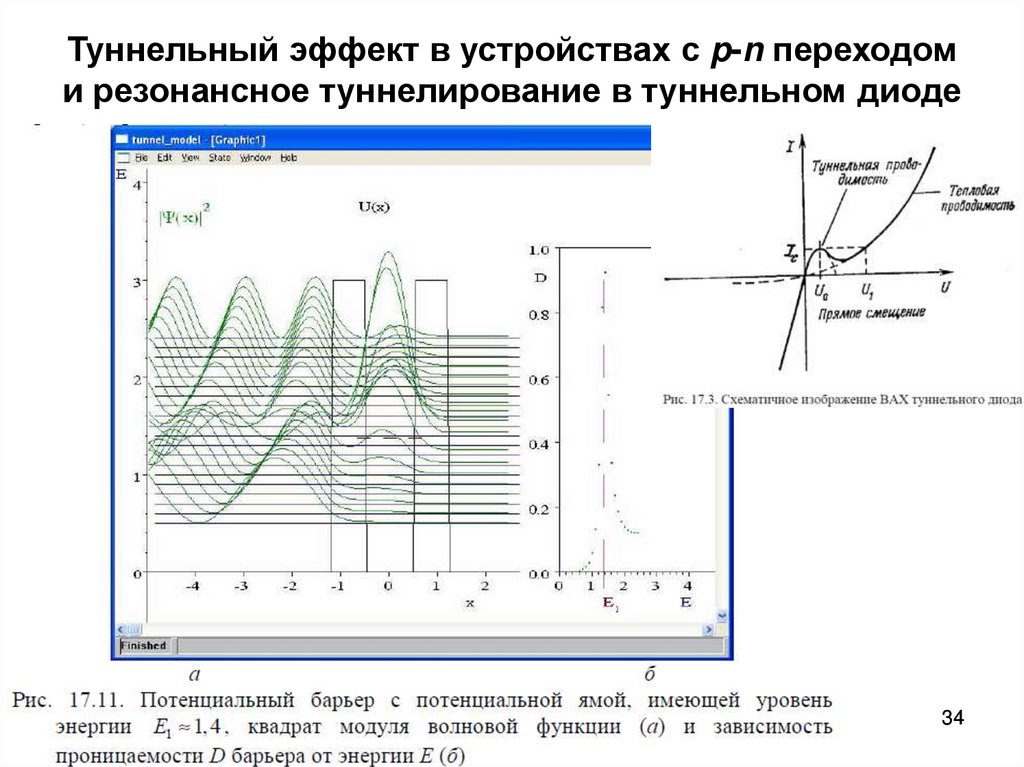
3334. Туннельный эффект в устройствах с p-n переходом и резонансное туннелирование в туннельном диоде
3435. Туннельный эффект при альфа-распаде
3536. Квазиклассическая формула для проницаемости потенциального барьера
2bD exp 2m U ( x) E dx
a
E U (a ) U (b)
a
b
m 2 2
формула для параболического барьера U ( x) B
x
2
b
2b
2
m 2 2
m 2
2
D exp 2m B E
x dx exp
2 m( B E ) 1
x dx
2
2( B E )
a
a
1
2
(B E)
exp
2 m( B E )
2
1
m
1 y dy exp 2 ( B E ) ,
2
E B
36
37. Квазиклассическая формула для проницаемости потенциального барьера
2bD exp 2m U ( x) E dx
a
E U (a ) U (b)
Здесь неприменима
a
b
Точки поворота для потенциального барьера
Квазиклассическое
приближение
Точная формула
Условие применимости D<<1
37
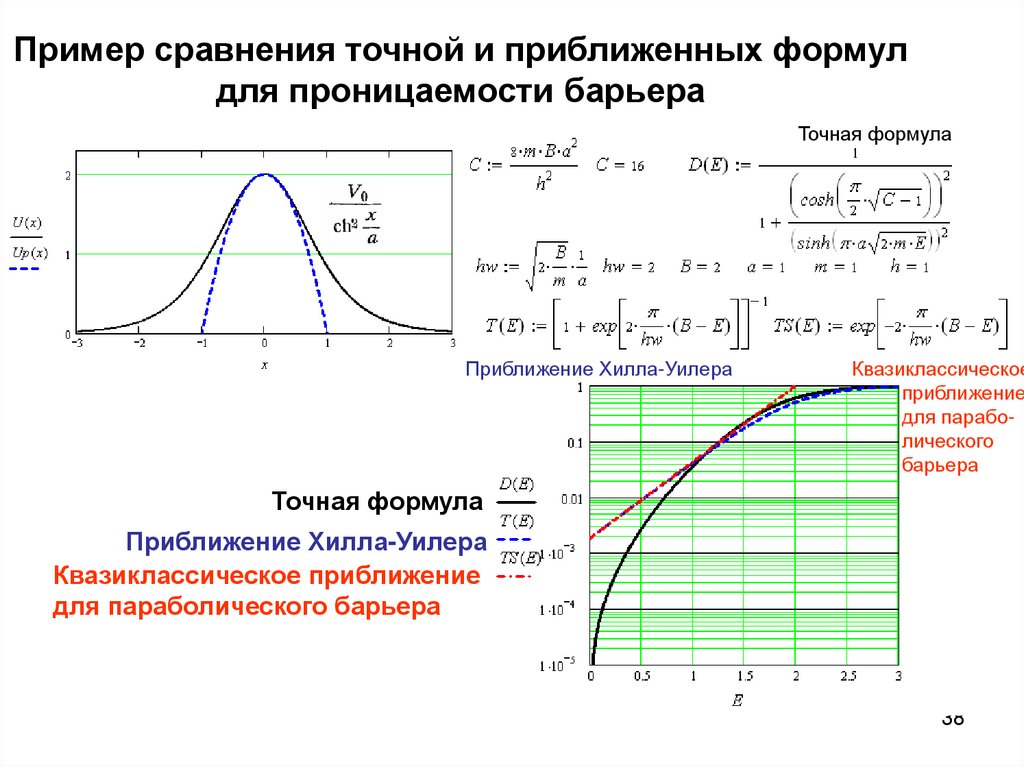
38. Пример сравнения точной и приближенных формул для проницаемости барьера
Точная формулаПриближение Хилла-Уилера
Квазиклассическое
приближение
для параболического
барьера
Точная формула
Приближение Хилла-Уилера
Квазиклассическое приближение
для параболического барьера
38
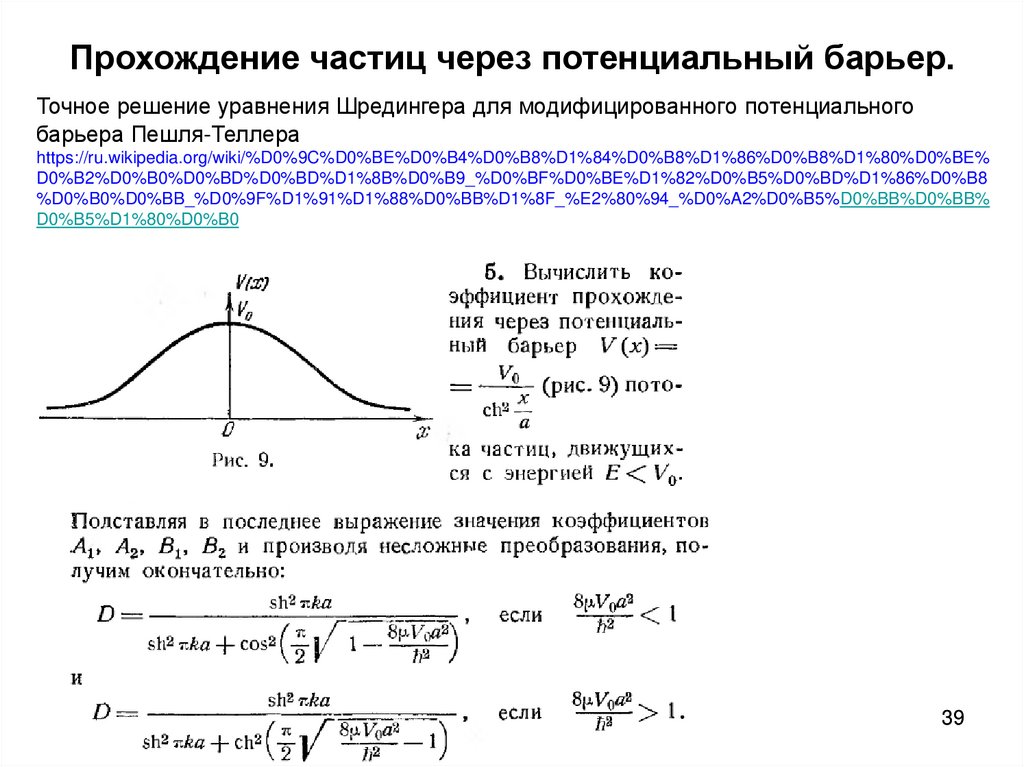
39. Прохождение частиц через потенциальный барьер.
Точное решение уравнения Шредингера для модифицированного потенциальногобарьера Пешля-Теллера
https://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%B4%D0%B8%D1%84%D0%B8%D1%86%D0%B8%D1%80%D0%BE%
D0%B2%D0%B0%D0%BD%D0%BD%D1%8B%D0%B9_%D0%BF%D0%BE%D1%82%D0%B5%D0%BD%D1%86%D0%B8
%D0%B0%D0%BB_%D0%9F%D1%91%D1%88%D0%BB%D1%8F_%E2%80%94_%D0%A2%D0%B5%D0%BB%D0%BB%
D0%B5%D1%80%D0%B0
39
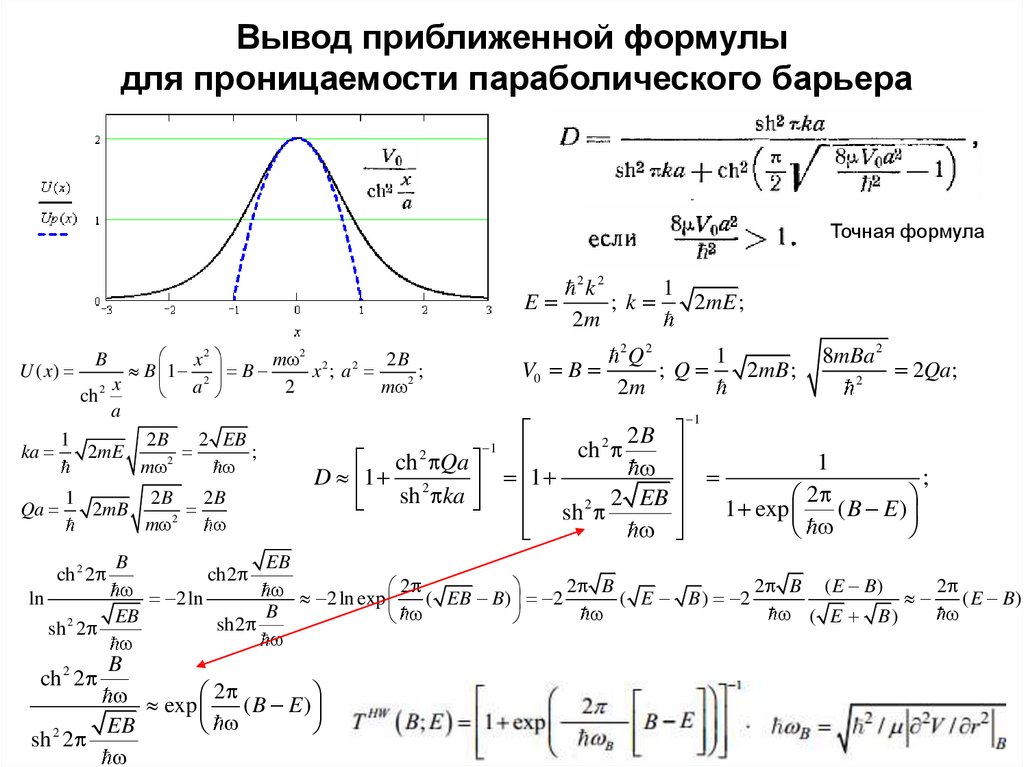
40. Вывод приближенной формулы для проницаемости параболического барьера
Точная формула2
k2
1
E
;k
2mE ;
2m
x2
m 2 2 2 2 B
U ( x)
B 1 2 B
x ;a
;
2
a
2
m
2 x
ch
a
B
ka
1
Qa
1
2mE
2B
2 EB
;
2
m
2mB
2B
2B
2
m
B
ch2
ln
2 ln
EB
2
sh2
sh 2
ch 2 2
2
Q2
1
V0 B
; Q
2mB ;
2m
8mBa 2
2
2Qa;
1
2 2B
1
ch
2
ch Qa
1
D 1 2
1
;
2
sh
ka
2
EB
2
1 exp
(B E)
sh
EB
2 ln exp 2 ( EB B) 2 2 B ( E B ) 2 2 B ( E B) 2 ( E B)
B
( E B)
B
exp 2 ( B E )
EB
2
sh 2
ch 2 2
40
41. Прохождение частиц через потенциальный барьер.
http://nrv.jinr.ru/nrv/webnrv/fusion/description/empiric.pdfПриближенная формула для
параболического барьера
с учетом центробежного
потенциала
формула Хилла-Уилера
e
41
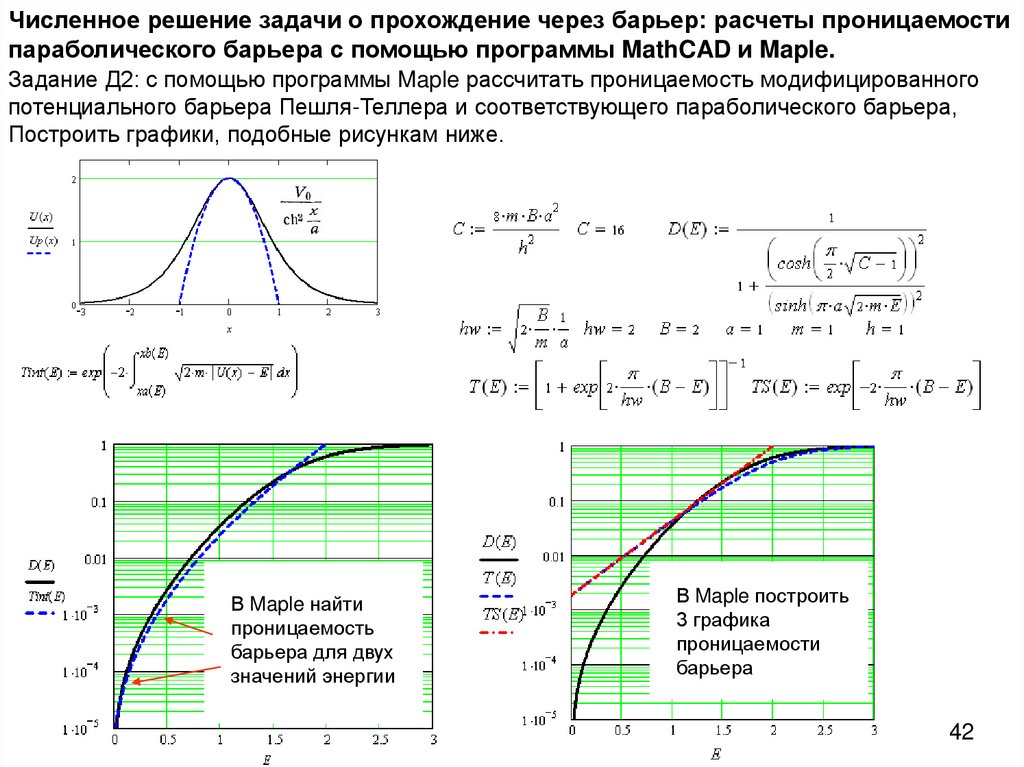
42.
Численное решение задачи о прохождение через барьер: расчеты проницаемостипараболического барьера с помощью программы MathCAD и Maple.
Задание Д2: с помощью программы Maple рассчитать проницаемость модифицированного
потенциального барьера Пешля-Теллера и соответствующего параболического барьера,
Построить графики, подобные рисункам ниже.
В Maple найти
проницаемость
барьера для двух
значений энергии
В Maple построить
3 графика
проницаемости
барьера
42
42
43.
Численное решение задачи о прохождение через барьер: расчеты проницаемостипараболического барьера с помощью программы MathCAD и Maple.
Квазиклассическое
приближение
для параболического
барьера
d
sin axdx
c
cos ad cos ac
a
a
В Maple построить
3 графика
проницаемости
барьера
43
44. Вопрос 6
1. Движение частиц в периодическомпотенциале.
2. Электронные состояния в кристаллах.
Зонные схемы.
44
45. Движение частиц в периодическом потенциале
Пусть периодический потенциал U имеет периоды трансляции a, b, c вдоль векторов
a , b , c примитивных трансляций пространственной решетки.
Согласно теореме Блоха собственные функции уравнения Шредингера
с периодическим потенциалом
имеют вид
2
2m
y U (r )y Ey
y k (r ) exp ikr uk (r )
где функция uk (r ) является периодической функцией в пространственной решетке.
Индексом функции Блоха и энергии E k ,a является волновой вектор
k
Для анализа свойств функций Блоха в пространстве волновых векторов строят так
называемую обратную решетку. Ее произвольный вектор задается формулами
G mA nB lC , exp iGri 1, ri ma nb lc
с помощью векторов примитивных трансляций обратной решетки
A 2
[bc ]
[ca ]
[ab ]
, B 2
, C 2
, V (a[bc ])
V
V
V
45
46. Энергия частиц в периодическом потенциале и зонные схемы
4647. Движение частиц в одномерном периодическом потенциале
22m
y U ( x)y Ey, U ( x) U ( x a)
2
k2
k
2m
Три первых энергетических зоны почти свободных электронов
в одномерном кристалле в (сверху вниз) расширенной зонной
схеме, в схеме приведенных зон и в периодической зонной схеме
47
48. Движение частиц в одномерном периодическом потенциале
22m
y U ( x)y Ey, U ( x) U ( x a)
Решение уравнения Шредингера для
свободного движения частиц (электронов),
соответствующее бегущим волнам,
y k ( x) C exp ikx ,
k kn, n 0, 1, 2,
k2
k
2m
, k
2
,
L
2
длина кристалла L>>a
В частности, при k=± /a имеются два приближенных
решения в виде стоячих волн
y1 ( x) cos x a , y1 ( x) cos 2 x a , (6.13)
2
y 2 ( x) sin x a , y 2 ( x) sin 2 x a .
2
(6.14)
Плотность вероятности нахождения электронов для
первого решения максимальна на положительных
ионах (см. рис.), для второго решения области
с большой вероятностью нахождения электронов
удалены от положительных ионов. Поэтому энергия
первого состояния меньше, чем второго,
а разница энергий равна ширине
запрещенной зоны.
48
49. Энеретические зоны в одномерном периодическом потенциале
Полученные состояния заполняются электронами по принципу Паули – состояние с определеннымзначением волнового числа k=n k, n=0,±1, ±2,… , может быть занято двумя электронами с
противоположными спинами. Различные случаи заполнения зонных структур могут привести к тому,
что рассматриваемый одномерный кристалл будет иметь свойства диэлектрика или проводника (металла),
см. рис.
Поверхность Ферми, определяемая
б
в
а
из условия
в пространстве волновых векторов
может иметь сложную форму.
Занятые состояния (заштрихованные области) в различных зонных структурах:
а – диэлектрик, б – металл с перекрытием зон, в – металл с частичным
заполнением верхней зоны
а
б
в
Схема заполнения электронами разрешенных энергетических зон в
диэлектрике (а), проводниках (б, в) (в), (металле) и полупроводниках с электронной (г) и дырочной 49
(д) проводимостью). Штриховкой показаны области разрешенных значений энергии, заполненные
электронами.
50. Энеретические зоны в одномерном периодическом потенциале и эффективная масса
Эффективная массаэлектрона
Таким образом, влияние
взаимодействия электрона с
атомами кристалла приводит к
тому, что во внешнем поле он
движется как частица с
эффективной массой m*.
Использование известного
значения m* позволяет в
дальнейшем проводить расчеты
без явного учета
кристаллического поля.
Аналогичным образом вводится
и эффективная масса дырки
50
51.
Диэлектрик51
52. Пример точного решения уравнения Шредингера для периодического потенциала – “гребенка” Дирака
5253.
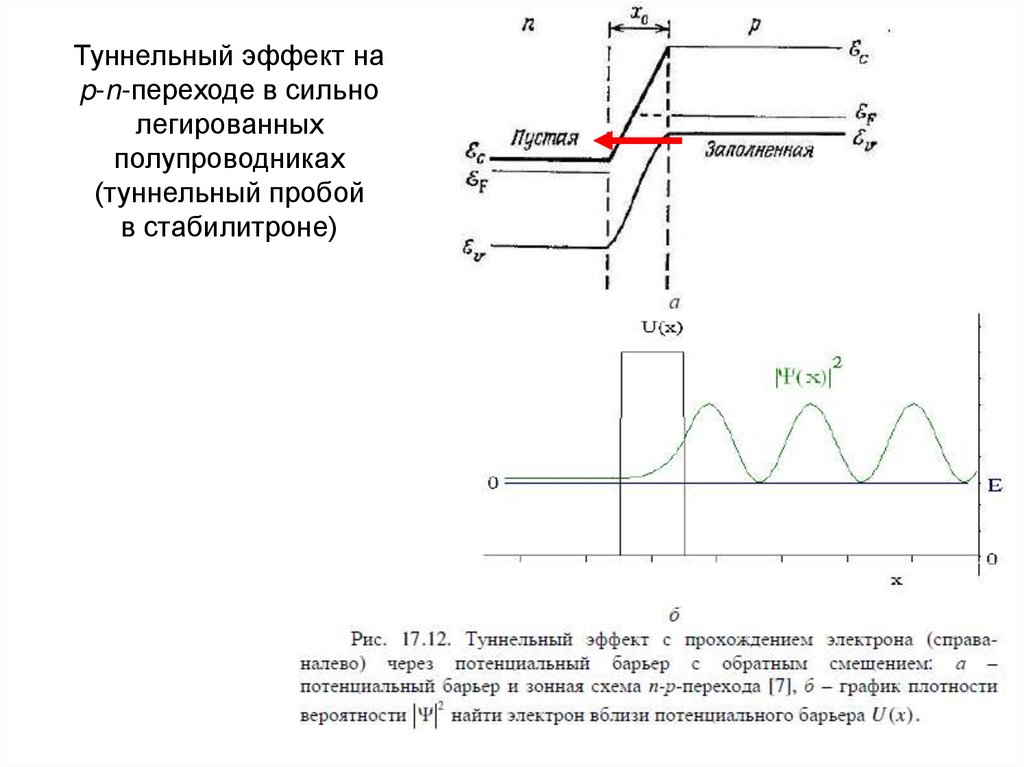
5354. Туннельный эффект на p-n-переходе в сильно легированных полупроводниках (туннельный пробой в стабилитроне)
55. Туннельный эффект на p-n-переходе в сильно легированных полупроводниках (туннельный диод)
56. Литература
2.3.
4.
Ландау Л.Д. Лифшиц Е.М. Краткий курс теоретической
физики. Т. 2. Квантовая механика. − М. Наука. 1971.
Давыдов А.С. Квантовая механика. − М. Наука. 1973.
Ситенко А.Г. Теория рассеяния. − Киев. “Вища школа”, 1975.
Фрауэнфельдер, Г. Субатомная физика. /Г. Фрауэнфельдер,
5.
Э. Хэнли. – М.: Мир. 1979.
Nuclear Reaction Video. База знаний по низкоэнергетическим
6.
ядерным реакциям. http://nrv.jinr.ru/nrv/.
Гольдман И. И., Кривченков В. Д. Сборник задач по квантовой
7.
механике. (ГИТТЛ, Москва, 1957).
Флюгге З. Задачи по квантовой механике. Т. 1. М.: Мир, 1974.
1.
56














































 physics
physics








