Квантовая теория. Лекция V

1. Квантовая теория

Семестр I
Журавлев В.М.

2. Лекция V

Стационарное уравнение
Шредингера

3.

Законы сохранения
классической механики
должны воспроизводится в
аналогичных условия в
квантовой теории!

4. Состояния с фиксированной энергией

Как вычислить состояния с
фиксированной энергией?

5. I. Состояния с фиксированной энергией для частицы в потенциальном поле

2
p
H ( p, x )
U ( x)
2m
2
pˆ
ˆ
H H ( p, x )
U ( xˆ )
2m
Состояние с фиксированной энергией ΨE
Hˆ E E E

6. I. Состояния с фиксированной энергией для частицы в потенциальном поле

В состоянии ΨE классическая энергия
Уравнение
для
состояний
с
совпадает с квантовой
фиксированной энергией в
ˆ поле
E
H
(
,
H
потенциальном
кл
E
E ) Eсил
называется стационарным
Уравнение для ΨE
уравнением Шредингера!
E U ( x) E E E
2
2m x
2
2

7.

II. Уравнение Шредингера
Пример.
Уравнение Шредингера для частицы в
пустом пространстве
U ( x) 0
E
E
E
2
2m x
2
2

8.

II. Уравнение Шредингера
Решение уравнения Шредингера для
частицы в пустом пространстве
2
E k E 0
2
x
2
2mE
k 2
p
k
2
E C1e
p
i x
C2e
p
i x

9.

Граничные условия и
типы движений
Как частица движется на
бесконечности?

10. II. Классификация движений

1. Движение частицы называется
финитным, если частица в любой
момент находится в заданной
ограниченной области пространства,
которая называется потенциальной
ямой
a x(t ) b,
pa p(t ) pb

11. II. Классификация движений

2. Движение частицы называется
ифинитным, если координата частица
асимптотически стремится к
бесконечности
x

12.

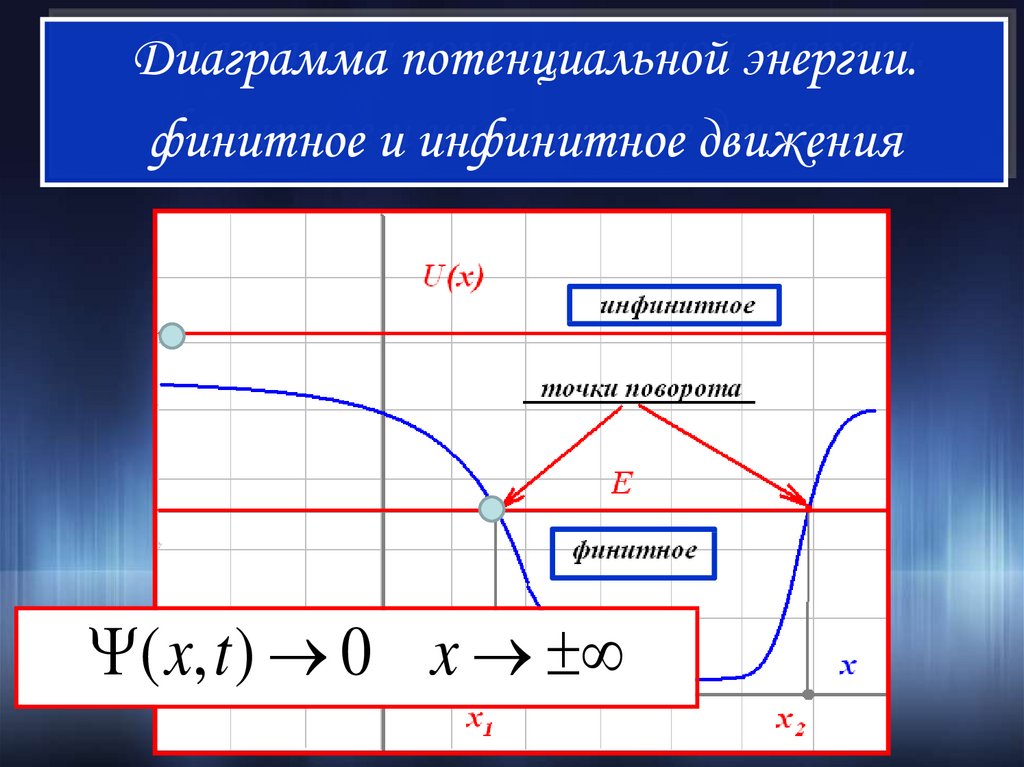
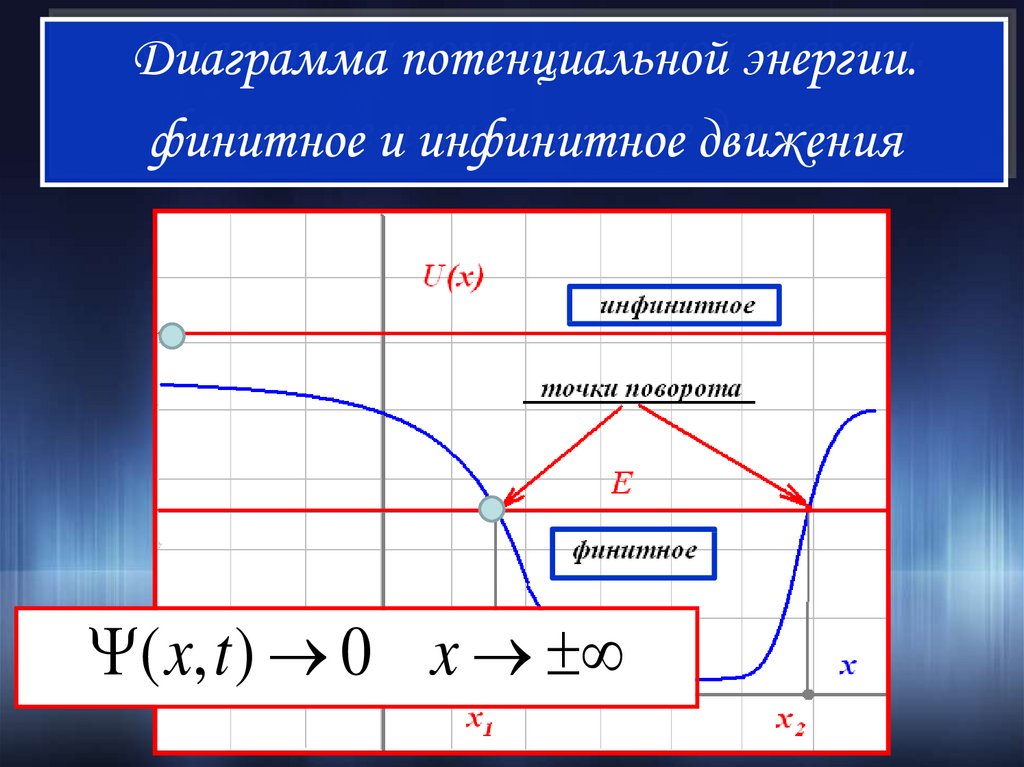
Диаграмма потенциальной энергии.
финитное и инфинитное движения
( x, t ) 0 x

13.

III. Финитное движение
В случае финитного движения
вероятность обнаружения частицы
на бесконечном удалении от
потенциальной ямы равна нулю!
( x, t ) 0 x

14.

III. Инфинитное движение
В случае инфинитного движения на
бесконечном удалении от области
взаимодействия частица ведет себя
как свободная и описывается
состоянием с фиксированной
энергией в пустом пространстве!
( x, t ) ae
p
i x
be
p
i x
, x

15.

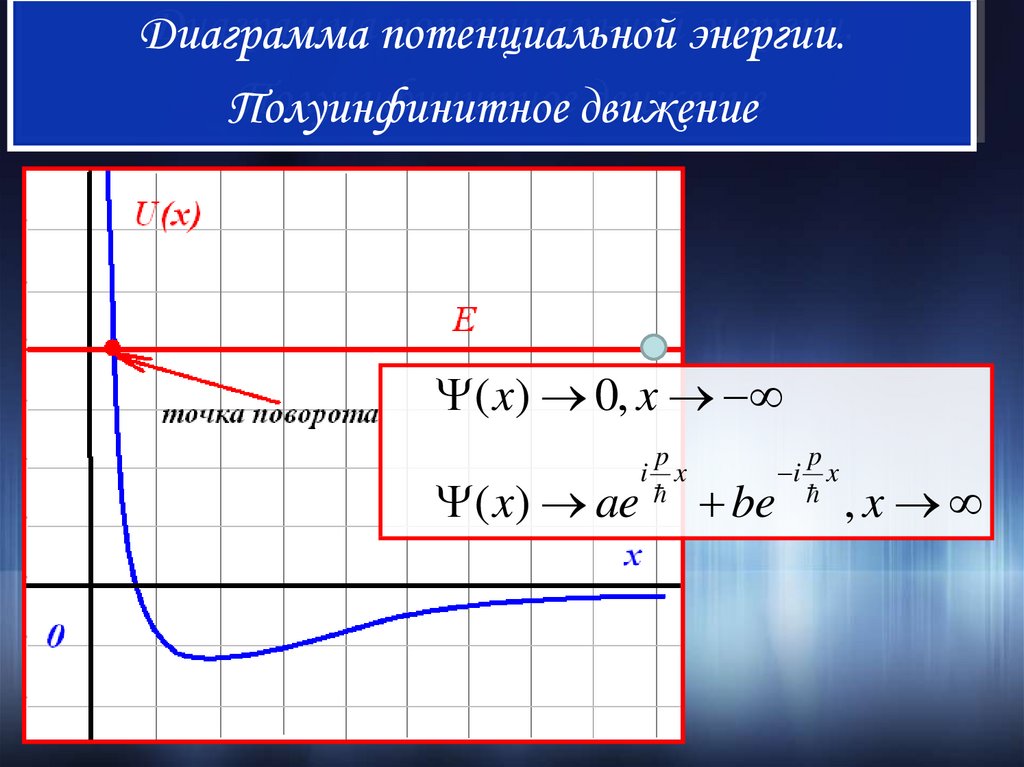
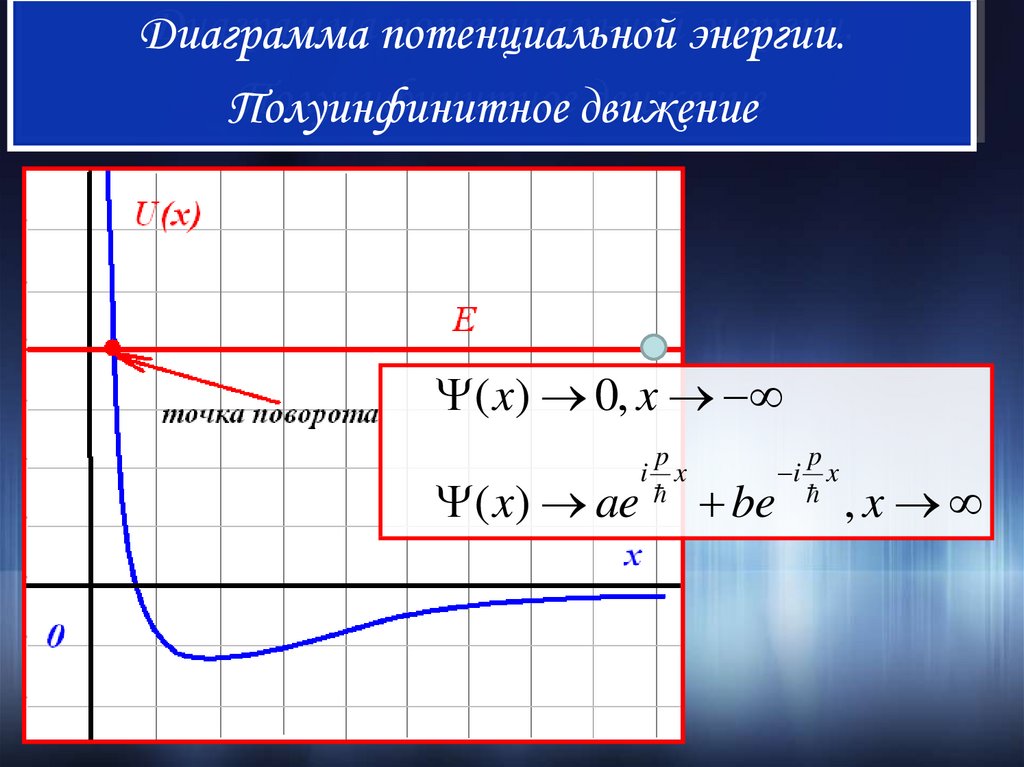
III. Полуинфинитное движение
В случае полуинфинитного движения
используются оба типа граничных условий.
В подбарьерной области волновая функция
убывает на бесконечности, а в
надбарьерной – стремится к волне
Де Бройля

16.

Диаграмма потенциальной энергии.
Полуинфинитное движение
( x) 0, x
( x) ae
p
i x
be
p
i x
,x

17.

IV. Постулат непрерывности
Все состояния квантовой системы
описываются всюду
непрерывными функциями
координат и времени!
( x 0) ( x 0), x [ , ]

18.

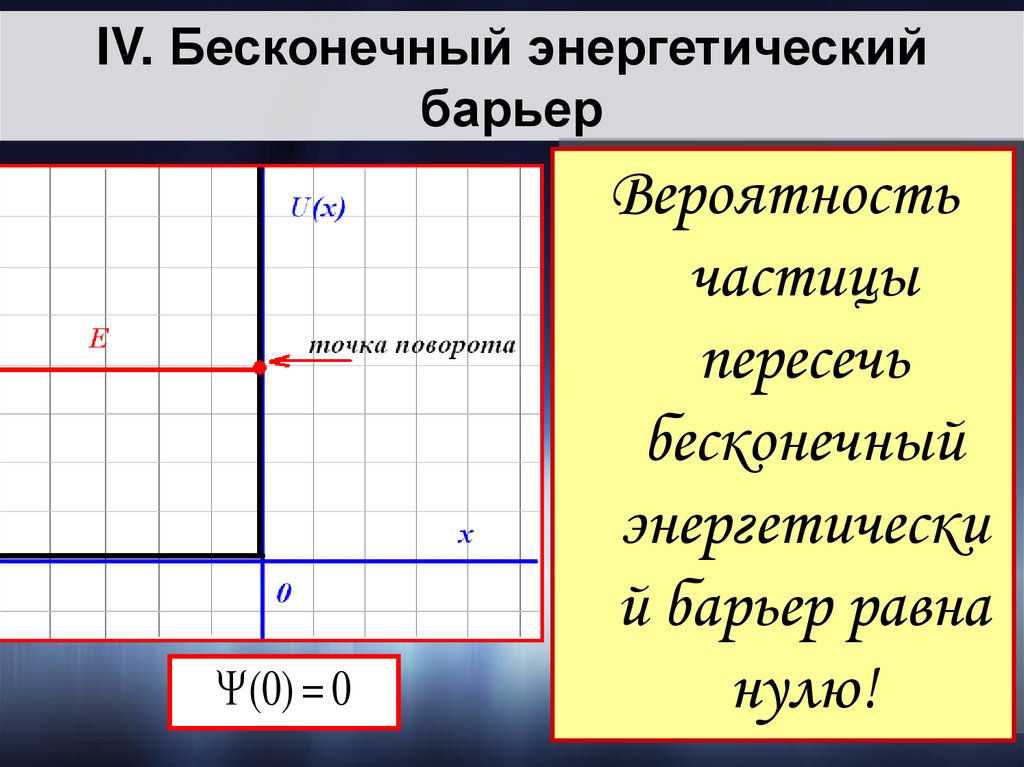
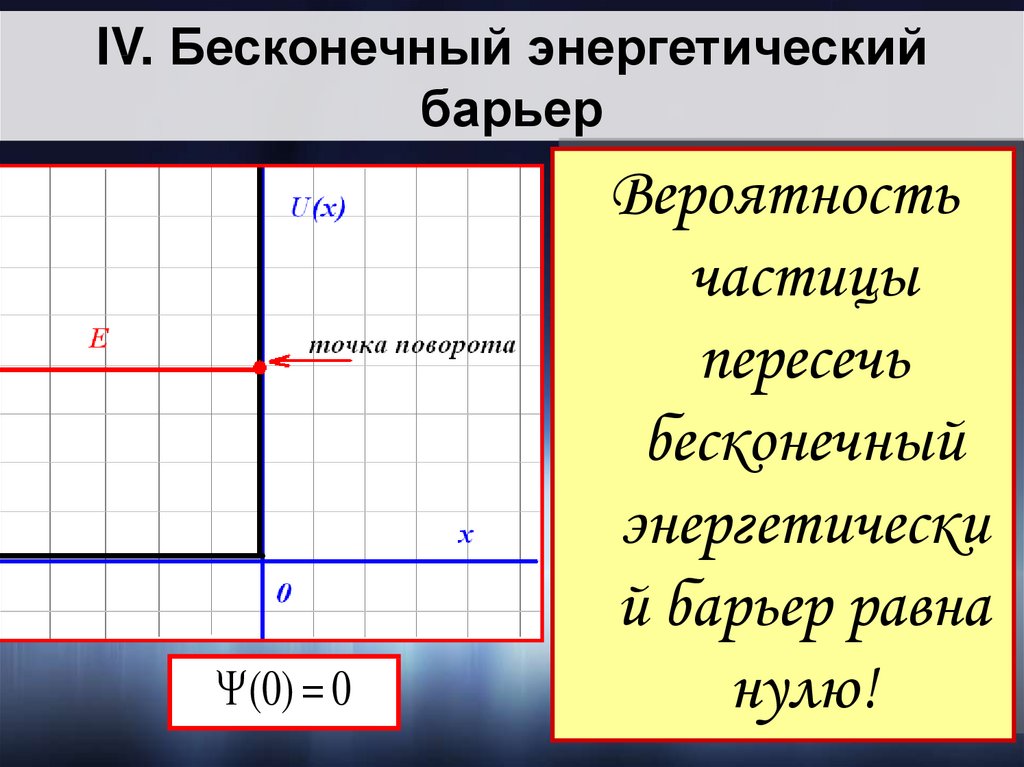
IV. Бесконечный энергетический
барьер
(0) 0
Вероятность
частицы
пересечь
бесконечный
энергетически
й барьер равна
нулю!

19. Бесконечно глубокая потенциальная яма

Частица в непроницаемом ящике!

20.

Бесконечно глубокая яма.
Постановка задачи.
ˆ
H
2
2m x
2
2
2
2
E k E 0
2
x
k2
2mE
0
2
k
p
0
(0) 0, (a) 0
E ( x) A sin( kx) B cos kx, 0 x a

21.

Бесконечно глубокая яма.
Собственные энергии.
E ( x) A sin( kx) B cos kx, 0 x a
E (0) B 0, (a) A sin( ka) 0
akn n дискретный спектр
n
2
En
kn
2m
2m a
2
2
2

22.

Бесконечно глубокая яма.
Собственные функции.
n
n ( x) A sin
x ,
a
0 x a
a
| ( x) | dx 1.
2
n
0
| A|
2
2 n
| A | sin
x dx
2
a
0
a
| A |2
2 n
0 1 cos a x dx 2 a 1
2 a

23.

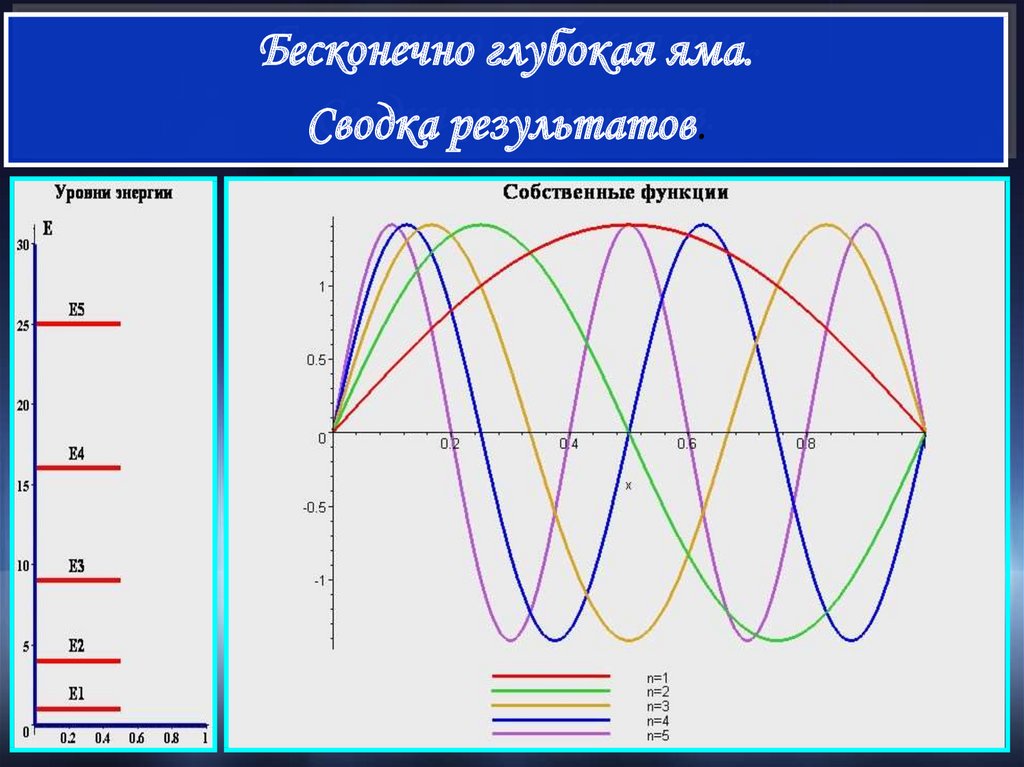
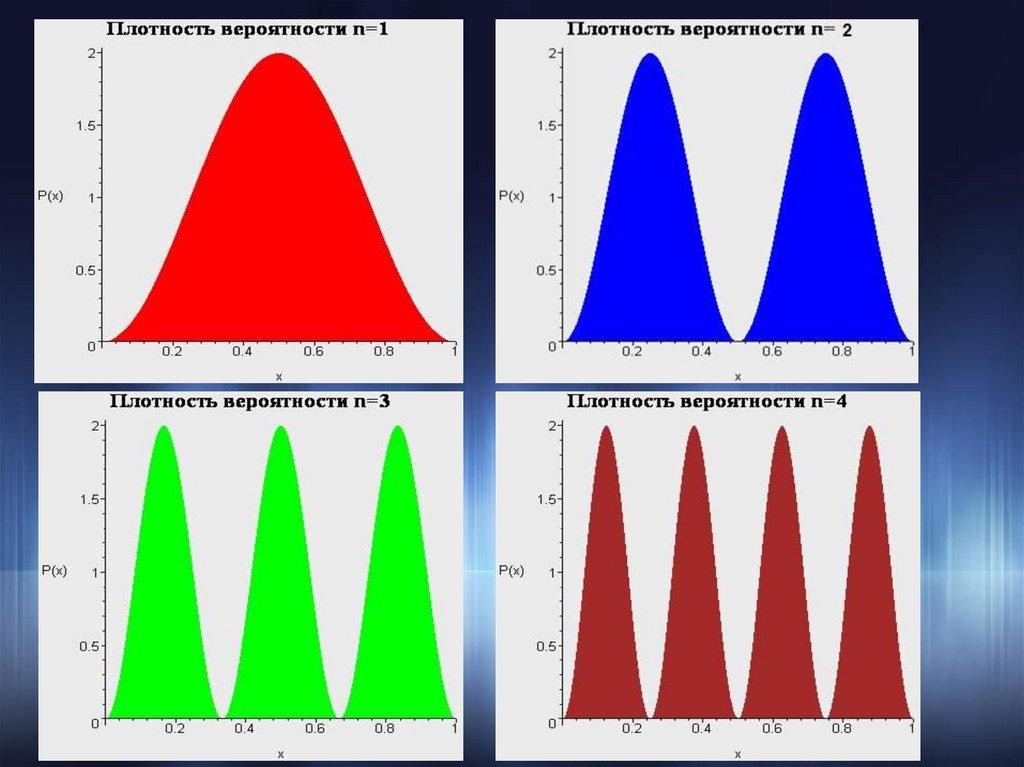
Бесконечно глубокая яма.
Сводка результатов.
n ( x)
2
n
sin
x ,
a
a
0 x a
n
2
En
kn
2m
2m a
2
2
2

24.

Бесконечно глубокая яма.
Сводка результатов.

25.

26.

Бесконечный энергетический барьер.
Постановка задачи.
2
2
Hˆ
2
2m x
2
2
k
E 0
E
2
x
k2
2mE
0
2
k
p
0
(0) 0,
( x) ae be
x
ikx
ikx
,

27.

Бесконечный энергетический барьер.
Собственные энергии.
ikx
( x) Ae Be , x 0
ikx
a A, b B, (0) A B 0
k любое непрерывный спектр
2
2
E
k
2m

28.

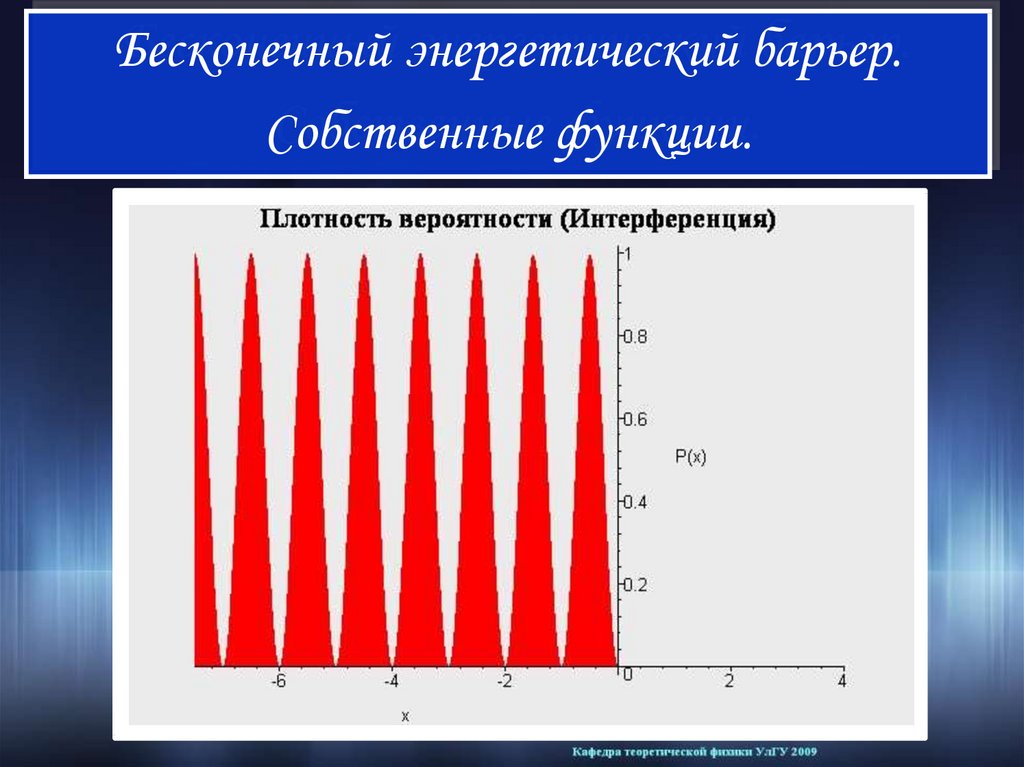
Бесконечный энергетический барьер.
Собственные функции.
(k , x) 2iA sin kx ,
0
4| A|
2
x a
sin( kx) sin( k ' x)dx (k k ' ).
Другая нормировка
A 1

29.

Бесконечный энергетический барьер.
Собственные функции.

30.

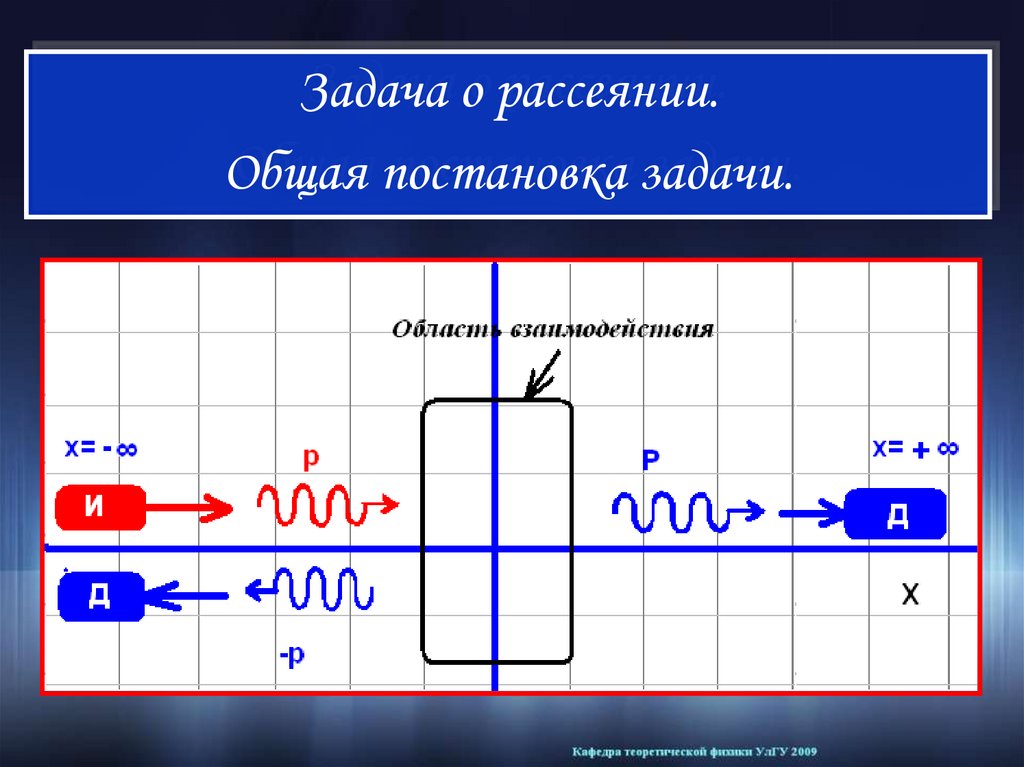
Задача о рассеянии.
Общая постановка задачи.

31. Повторяем граничные условия

Условия на границах в зависимости
от типа движения!

32.

Диаграмма потенциальной энергии.
финитное и инфинитное движения
( x, t ) 0 x

33.

Диаграмма потенциальной энергии.
Полуинфинитное движение
( x) 0, x
( x) ae
p
i x
be
p
i x
,x

34.

IV. Постулат непрерывности
Все состояния квантовой системы
описываются всюду
непрерывными функциями
координат и времени!
( x 0) ( x 0), x [ , ]

35.

IV. Бесконечный энергетический
барьер
(0) 0
Вероятность
частицы
пересечь
бесконечный
энергетически
й барьер равна
нулю!

36. Гармонический осциллятор

Как описываются квантовые
колебания?