Internal Combustion Engine Induction Tuning

1. Internal Combustion Engine Induction Tuning

ME 468 Engine Design
Professor Richard Hathaway
Department of Mechanical and Aeronautical Engineering

2. Port Sizing Considerations

3. Swept and Displaced Volumes

• Swept Volume/cylinder:
Vs=
4
d s Ap s
2
B
Inlet Port
s x Ap
Vs = swept volume
dB = bore diameter
s = stroke
Note: In valve design the Volume which flows into
the cylinder must equal the volume which flows
through the inlet port. The velocity past the valve
must then be considerably greater than the velocity
in the cylinder.
s

4. Port Sizing and Mach Index (Z)

• Mach Index is the ratio of the velocity of the gases flow area to the speed of
sound
2
b
Piston speed
d
Z=
n x d 2p Speed of Sound
Db = cylinder bore dia.
Dp = port dia.
n = number of ports
For mean values:
Piston speed MEAN 2 RPM stroke
2
d b 2 RPM stroke
Z=
2
n x d p Speed of Sound

5. Port Sizing and Mach Index (Z)

• For instantaneous relationships:
2
db
=
Zi
n x d 2p
RPM
2 s
s
Sin
+
Sin (2 )
60 2
4L
1
Speed of Sound
cd
s = length of stroke
L = length of connecting rod
θ = crank position
Cd = flow coefficient

6. Port Sizing and Mach Index (Z)

• Speed of Sound:
– Temperature and F/A ratio dependant
– At Standard Temperature and Pressure
c = 1100 ft/sec
o
c ft/ sec = 49.02 T R
c = 340 m/sec
o
cm/ sec = 20.05 T K

7. Port Sizing and Mach Index (Z)

• Modern performance engines will use multiple inlet and
exhaust valves per cylinder.
• Many are using multiple intake runners per cylinder to
improve cylinder filling over a broader range of RPM.
– A single runner is used at lower RPM while a second runner will
be opened at higher RPM.
– The second and the combined each have their own tuning peak.

8. Inlet Air Density and Performance

9. Inlet air density

• Law of Partial Pressures:
Pt = Partial Pressures
Pi = Pair + P fuel vap + Pwater vap
• If each is considered as a perfect gas
Mass
M
P =
=
Molecular wt.
m

10. Inlet air density

• Inlet Pressures and Densities:
P air =
P air
Pinlet P air + P fuel + P water
M a / ma
=
M a / ma + M f / m f + M w / m w
ma = 29 mw = 18 mgas = 113
Fc = chemically correct mix
Fi = % vaporized (Fc)

11. Inlet air density

• Inlet Pressures and Densities:
Pa
M a / 29
=
Pi
M a / 29 + M f / m f + M w / mw
1
Pa
=
1 + F i (29 / m f ) + h(1.6)
Pi
• From Ideal Gas Law
mx p
=
R xT
29 x Pa
a =
R xTi
R = 1545 ft-lb/(lbm-mole-oR)

12. Inlet air density

Inlet Densities:
29 x P a
a =
R xTi
29 x Pi
1
a =
R x T i 1 + F i (29 / m f ) + h(1.6)
for P in psia and T in oR
2.7 x Pi
1
a =
1
+
(29
/
)
+
h(1.6)
Ti
F
m
i
f

13. Inlet air density

• Example Problem:
– Find the change in indicated power when changing
from Gasoline to Natural Gas fuels
Assume:
Pi = 14.0 psia
Ti = 100oF
= 1.2 => 20 % Rich
h = 0.02 lbm/lbm air
GASOLINE:
F/A = 1.2 x 1/14.8 = 0.081 lbfuel/lbair
Assume fuel is 40% vaporized
(Use fuel distilation curves)

14. Inlet air density

Gasoline:
mix =
2.7 x 14.0
1
460 +100 1+(.4)(.081)(29 / 113)+0.02(1.6)
mix = 0.06488 lbm / ft 3
Natural gas:
F/A = 1.2 x 1/17.2 = 0.0697 lbfuel/lbair
Fuel is a gaseous fuel and is 100% vaporized

15. Inlet air density

• NATURAL GAS:
2.7 x Pi
1
a =
1
+
(29
/
)
+
h(1.6)
Ti
F
m
i
f
2.7 x 14.0
1
mix =
460 +100 1 + (1)(.06977)(29 / 18.3) + 0.02(1.6)
mix = 0.0591 lbm / ft 3

16. Inlet air density

• NATURAL GAS:
mix =
2.7 x 14.0
1
460 +100 1 + (1)(.06977)(29 / 18.3) + 0.02(1.6)
mix = 0.0591 lbm / ft 3
• INDICATED POWER RATIO:
Ihpnat gas
Ihp gasoline
=
mix
c
nat gas
gasoline
x F / A x ecnatgas
x F / A x ecgasoline

17. Inlet air density

Indicated power ratio:
Ihpnat gas
Ihp gasoline
Ihpnat gas
Ihp gasoline
=
mix
c
nat gas
gasoline
x F / A x ecnatgas
x F / A x ecgasoline
0.0591 x 0.0697 x 21,800
=
0.06488 x 0.081 x 19,000
= .8993 90%
The above indicates an approximate 10% loss in power
output by changing to the gaseous fuel.

18. Inlet air density

Ihpnat gas
Ihp gasoline
0.0591 x 0.0697 x 21,800
=
0.06488 x 0.081 x 19,000
= .8993 90%
Note: Gasoline performance decreases more rapidly
with increasing temperature.

19. ACOUSTIC MODELING

20. Induction System Comparisons

Courtesy: Dan Butts, Derek Harris, Chris Brockman, Tiffany Dickinson

21. Acoustic Modeling

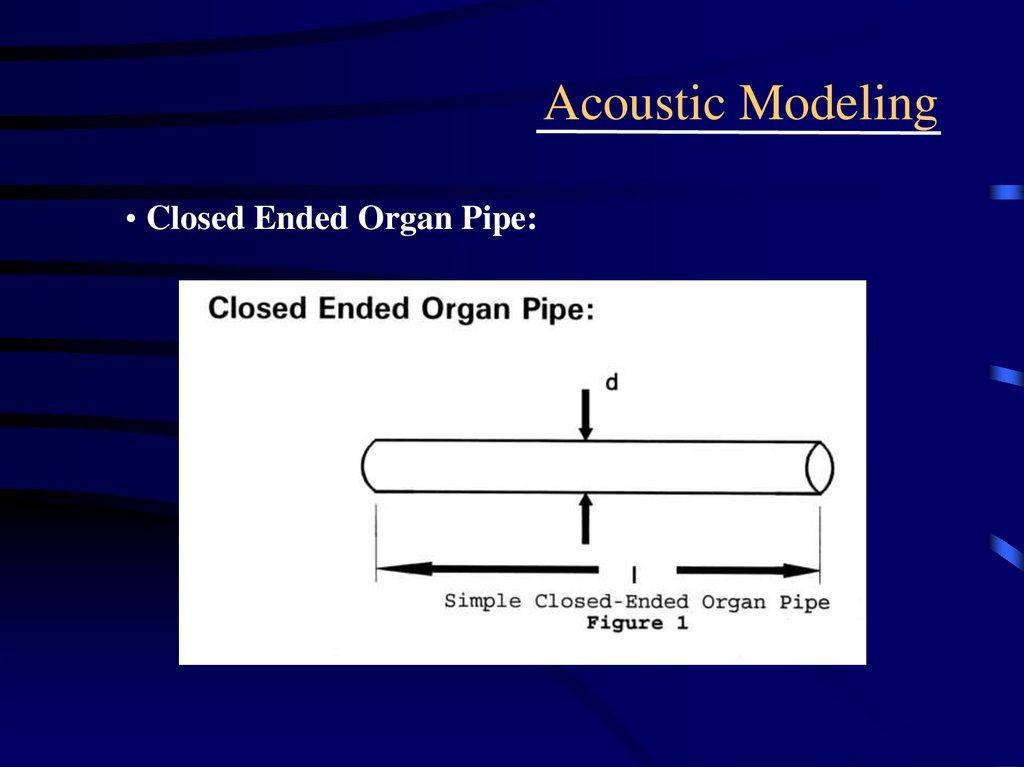
• Closed Ended Organ Pipe:

22. Acoustic Modeling

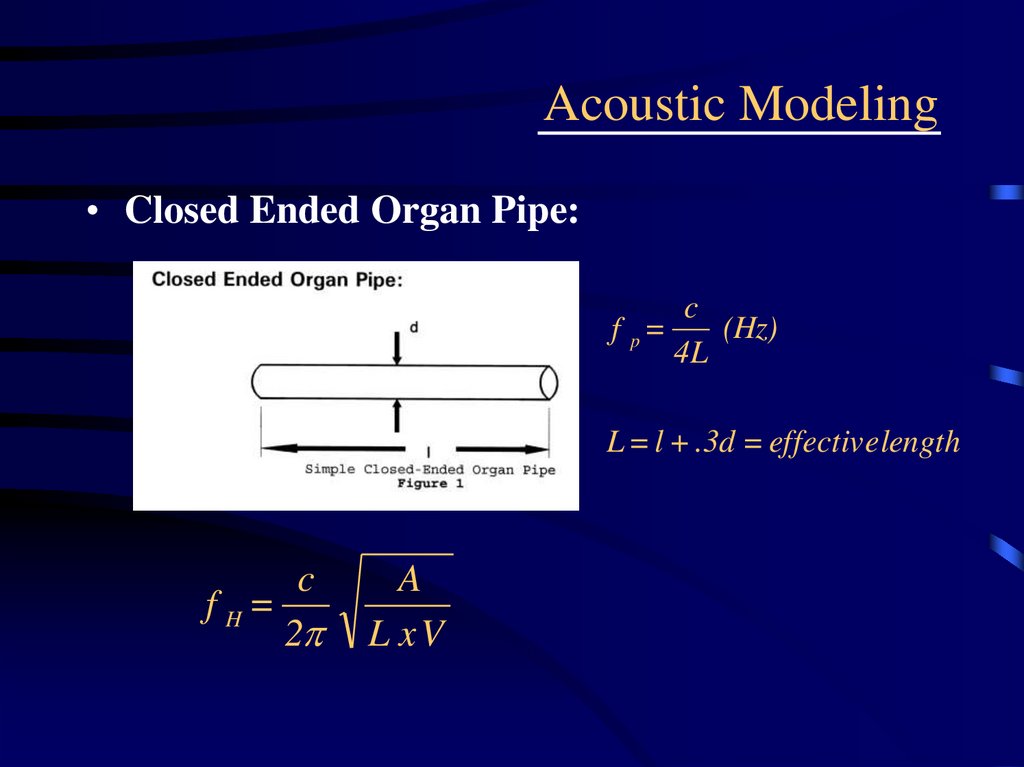
• Closed Ended Organ Pipe:
c
(Hz)
f p=
4L
L = l + .3d = effective length
c
f H=
2
A
L xV

23. Acoustic Modeling

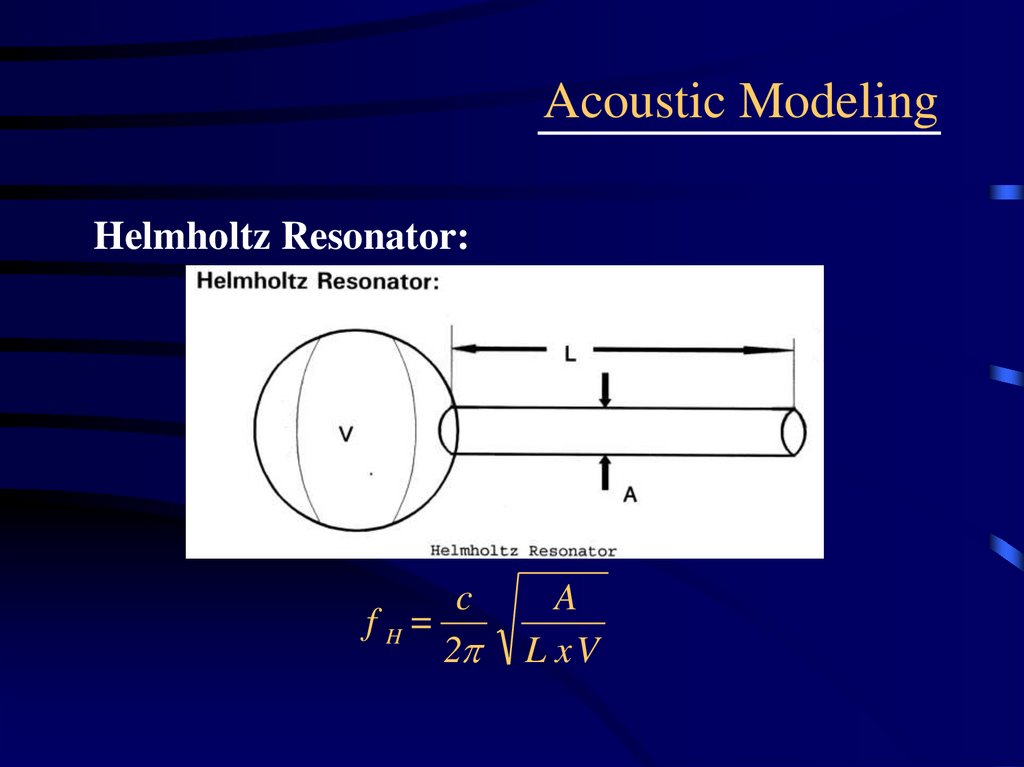
Helmholtz Resonator:
c
f H=
2
A
L xV

24. Build Considerations

• Variable Length Runners for RPM
matching
• Materials Selection Criteria:
– Weight, Fabrication, Surface Finish,
Heat Isolation
• Intake placement
– Isolate from heat sources (Engine,
Exhaust, Radiator, Pavement)
• Fuel Injector Placement
Courtesy: Dan Butts, Derek Harris, Chris Brockman, Tiffany Dickinson

25. Acoustic Modeling

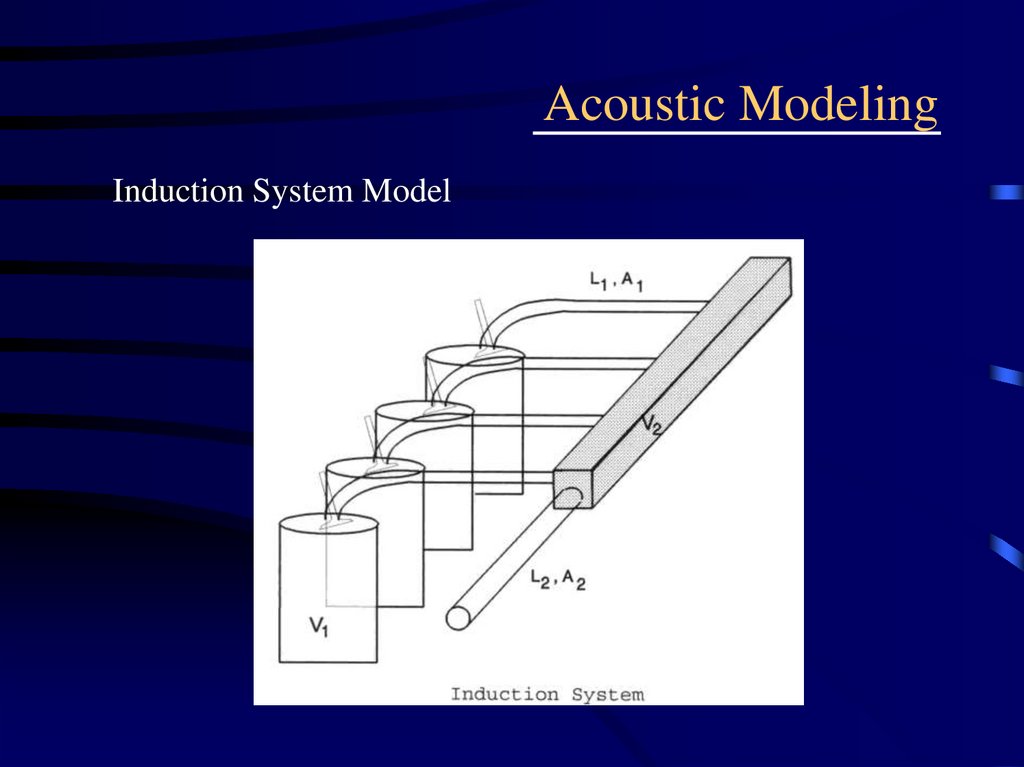
Induction System Model

26. Multiple Stack with pressure box

Courtesy: Dan Butts, Derek Harris, Chris Brockman, Tiffany Dickinson

27. Acoustic Modeling

For a single degree of freedom system
A1 CR - 1
N p = K 1 x C x
L1 V d CR + 1
A1 = Average Area of Runner and Port
L1 = LPort + Lrunner
K1 = 77 (English)
K1 = 642 (Metric)
C = Speed of Sound

28. Individual Throttle Body with Plenum

Courtesy: Dan Butts, Derek Harris, Chris Brockman, Tiffany Dickinson

29. Helmholtz Tuning

• Writing Clearance Volume in Terms of Compression
Ratio:
V S + V CC
CR =
V CC
V CC =
VS
(CR - 1)
• The Primary Volume is considered to be the Cylinder
Volume with the Piston at mid-stroke (effective volume).
V P=
VD
VD
+
2 (CR - 1)
V eff =
V D (CR - 1) + 2 V D
2(CR - 1)
V D (CR + 1)
V eff =
2 (CR - 1)

30. Helmholtz Tuning

• The tuning peak will occur when the natural Helmholtz
resonance of the cylinder and runner is about twice the
piston frequency.
Volume (V1)
= Cylinder Volume
Volume (V2)
= Volume in the path from V1 to the Plenum
Using Engelman's electrical analogy we can define the
system as a system defined by capacitances and
inductances.
L
Inductance ( I i ) =
A i

31. Helmholtz Tuning

• The EFFECTIVE INDUCTANCE for a pipe with
different cross-sections may be defined as the sum of
inductances of each section.
L L
L
( I e ) = + + ....+
A i A i+1
A n
The INDUCTANCE RATIO (a) is defined as the ratio of
the secondary inductance to the primary inductance.

32. Helmholtz Tuning

• INDUCTANCE RATIO (a)
L
A
a = 2
L
A 1
• The CAPACITANCE RATIO (b) is defined as the ratio
of the Secondary Volume to the Primary Volume.
CR - 1
V2 V2
b=
=
x2
CR + 1
V eff V D
V2 = Secondary Volume
= Volume of Intake Runners that are ineffective (n-1)

33. Helmholtz Tuning

• Calculate the Separate Inductances:
I port =
L port
A port
Lrunner
=
I runner
Arunner
L plenum
A plenum
I T .body =
I plenum =
• Determine the Inductance Ratio (a)
L
A 2 I T .body + I plenum
a=
L
I port + I runner
A 1
LT .body
AT .body

34. Helmholtz Tuning

• Determine the Capacitance Ratio (b)
V eff
b=
(n - 1) x V runner
• Determine the Induction system Resonances
f 1=
1
2
A- B
2 x a b (IND )1 x V eff
A = (a b + a + 1)
f 2=
1
2
A+ B
2 x a b (IND )1 x V eff
B = (a b + a + 1 )2 - 4 a b
(IND)1 = Inductance of the primary length
(IND)1 = Iport + Irunner

35. Helmholtz Tuning

• Determine the Primary Resonance:
f p=
1
2
1
x V eff
I port + I runner
Determine the Frequency Ratios:
f1
X 1=
fp
f2
X 2=
fp
• Determine the Tuning Peak:
A1 CR - 1
=
x
C
x
N p K1
L1 V d CR + 1
A1 = Average Area of Runner and Port
L1 = LPort + Lrunner
K1 = 77 (English)
K1 = 642 (Metric)
C = Speed of Sound

36. Helmholtz Tuning

• Intake Tuning Peaks become:
N2= X 2 x N p
N1= X 1 x N p
f 1=
1
2
A- B
2 x a b (IND )1 x V eff
f 2=
1
2
A+ B
2 x a b (IND )1 x V eff
X 1=
f1
fp
X 2=
f p=
f2
fp
A1 CR - 1
N p = K 1 x C x
L1 V d CR + 1
1
2
1
x V eff
I port + I runner

37. Helmholtz Tuning

• A combined equation is possible indicating it’s 2nd order
P 2 V 2 CR - 1 P +
+ 1
+
eff
CR
+
1
eff
V
d
N 1,2 = 77( C S )
L
P=
A 2
1
2
P 2 V 2 CR - 1 P P 2 V 2 CR - 1
eff V CR + 1 + eff + 1 - 4 eff V CR + 1
d
D
4 PV 2
L
EFF =
A eff
2
Vd=
V 2 = ( Lman + L port )* Am * (NC - 1)
4
* b2 * s

38. David Visard’s “Rule of thumb” Equations

Using Visard's Equation for Runner Length
1. Starting point of 7 inches for 10,000 RPM
2. Add length of 1.7 inches for each 1000 RPM
less
Using Visard's Equation for Runner Diameter

39. The End

Thank You!