Similar presentations:
Drilling Engineering
1.
Drilling EngineeringDrilling Engineering – PE 311
Hydraulics of Drilling Fluids
Prepared by: Tan Nguyen
2.
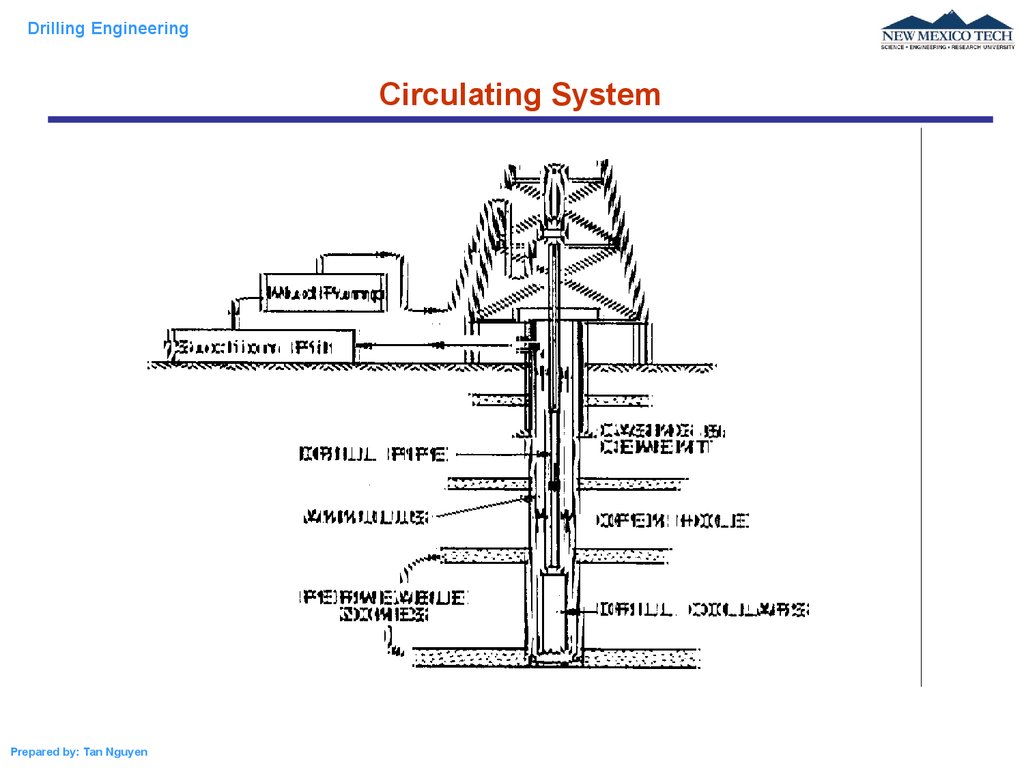
Drilling EngineeringCirculating System
Prepared by: Tan Nguyen
3.
Drilling EngineeringHydrostatic Pressure in Liquid Column
P
For incompressible fluids, the specific weight of the
liquid in field unit is given by
p 0.052 D p0
P + dP
If P0 = 0 then
p 0.052 D
The fluid density
Prepared by: Tan Nguyen
p
0.052 D
4.
Drilling EngineeringHydrostatic Pressure in Liquid Column
Example: Calculate the static mud density required to prevent flow from a
permeable stratum at 12,200ft if the pore pressure of the formation fluid is
8500psig.
Solution:
p
8500
13.4lbm / gal
0.052 D 0.052 12,200
The mud density must be at least 13.4 lbm/gal
Prepared by: Tan Nguyen
5.
Drilling EngineeringHydrostatic Pressure in Gas Column
dp 0.052 dD
EOS of gas:
p
p0
P0
m pM
pM
V ZRT 80.3 Z T
dp
0.052 p M
dD
80.3 Z T
dp
M
p 1544 Z T
p p0 e
Prepared by: Tan Nguyen
m
RT
M
pV Z n R T Z
D
D0
P0 + dP
dD
M ( D D0 )
1544 Z T
6.
Drilling EngineeringHydrostatic Pressure in Gas Column
A well contains tubing filled with methane gas (MW = 16) to a vertical depth of
10000ft. The annular space is filled with a 9.0 lbm/gal brine. Assuming ideal gas
behavior, compute the amount by which the exterior pressure on the tubing
exceeds the interior tubing pressure at 10,000ft if the surface tubing pressure is
1000 psia and the mean gas temperature is 140F. If the collapse resistance of the
tubing is 8330 psi, will the tubing collapse due to the high external pressure?
Prepared by: Tan Nguyen
7.
Drilling EngineeringHydrostatic Pressure in Gas Column
The pressure in the annulus (external pressure) at D = 10,000 ft is
P2 = 0.052 * 9.0 * 10,000 + 14.7 = 4,695 psia
The pressure in the tubing (internal pressure) at D = 10,000ft
p p0 e
M ( D D0 )
1544 Z T
1000 e
16*10000
1544*( 460 140 )
1188 psia
Pressure difference = p2 – p = 4695 – 1188 = 3507 < 8330 psia
The tubing will withstand the high external pressure
Prepared by: Tan Nguyen
8.
Drilling EngineeringHydrostatic Pressure in Complex Fluid Column
pi 1 pi p pi 0.052 i 1 Di 1 Di
p1 p0 0.052 1 D1 D0
p2 p1 0.052 2 D2 D1
p3 p2 0.052 3 D3 D2
pn pn 1 0.052 n Dn Dn 1
n
p n p 0 0.052 i ( Di Di 1 )
i 1
Prepared by: Tan Nguyen
9.
Drilling EngineeringHydrostatic Pressure in Complex Fluid Column
=?
p a p 0 0.052 (10.5 7,000 8.5 300 12.7 1700
16.7 1,000 9.0 10,000) 0 1266 1266 psig
Prepared by: Tan Nguyen
10.
Drilling EngineeringEquivalent Circulating Density (ECD)
The effective density exerted by a circulating fluid against the formation that takes
into account the pressure drop in the annulus above the point being considered.
The ECD is calculated as:
– mud density, ppg
P – Sum of the hydrostatic pressure and the frictional pressure drop in the annulus
between the depth D and surface, Psig
D – the true vertical depth, ft
Prepared by: Tan Nguyen
11.
Drilling EngineeringEquivalent Circulating Density (ECD)
Example: A 9.5-PPG drilling fluid is circulated through the drill pipe and the annulus.
The frictional pressure losses gradient in the annulus is 0.15. Calculate the
equivalent circulating density in PPG.
Solution:
= 9.5 + P/0.052 = 9.5 + 0.15 / 0.052 = 12.4 PPG
Prepared by: Tan Nguyen
12.
Drilling EngineeringBuoyancy
We W Pb PT A
We o gVo l gHA
PT
Fb
H
We o gVo l gVo
We W Wbo
gV
We o gVo 1 l o
o gV
l
We Wo 1
o
Prepared by: Tan Nguyen
W
Pb
+
We , W, Wbo – effective weight, weight of the object
in air, and buoyant force.
l and o - densities of liquid and the object
13.
Drilling EngineeringBuoyancy
10,000 ft of 19.5-lbm/ft drillpipe and 600 ft of 147 lbm/ft drill collars are suspended
off bottom in a 15-lbm/gal mud. Calculate the effective hook load that must be
supported by the derrick. Density of steel is 65.5 lbm/gal
Solution:
W = 19.5 * 10000 + 147 * 600 = 283200 lbm
We = W(1 - f/ s) = 283200 * (1 - 15/65.5) = 218300 lbm
(density of steel = 65.5 lbm/gal = 490lbm/cu ft)
Prepared by: Tan Nguyen
14.
Drilling EngineeringFlow Through Jet Bits
Energy balance:
p2 p1 0.052 D2 D1 8.074 *10 4 v22 v12 Pp p f
Pp is heat entering the system
Pf is heat loss due to friction
Prepared by: Tan Nguyen
15.
Drilling EngineeringFlow Through Jet Bits
Applying the energy equation for a flow through a nozzle with neglecting:
(1)effects of elevation: D2 - D1 = 0
(2)effects of uptream velocity v o = 0
(3)Heat entering the system Pp = 0 and friction loss Pf = 0
p 2 p1 0.052 D2 D1 8.074 *10 4 v 22 v12 Pp p f
Prepared by: Tan Nguyen
16.
Drilling EngineeringFlow Through Jet Bits
p 2 p1 8.074 * 10 4 v n2
vn
vn C d
pb
8.074 10 4
pb
8.074 10 4
C d correction factor
Prepared by: Tan Nguyen
17.
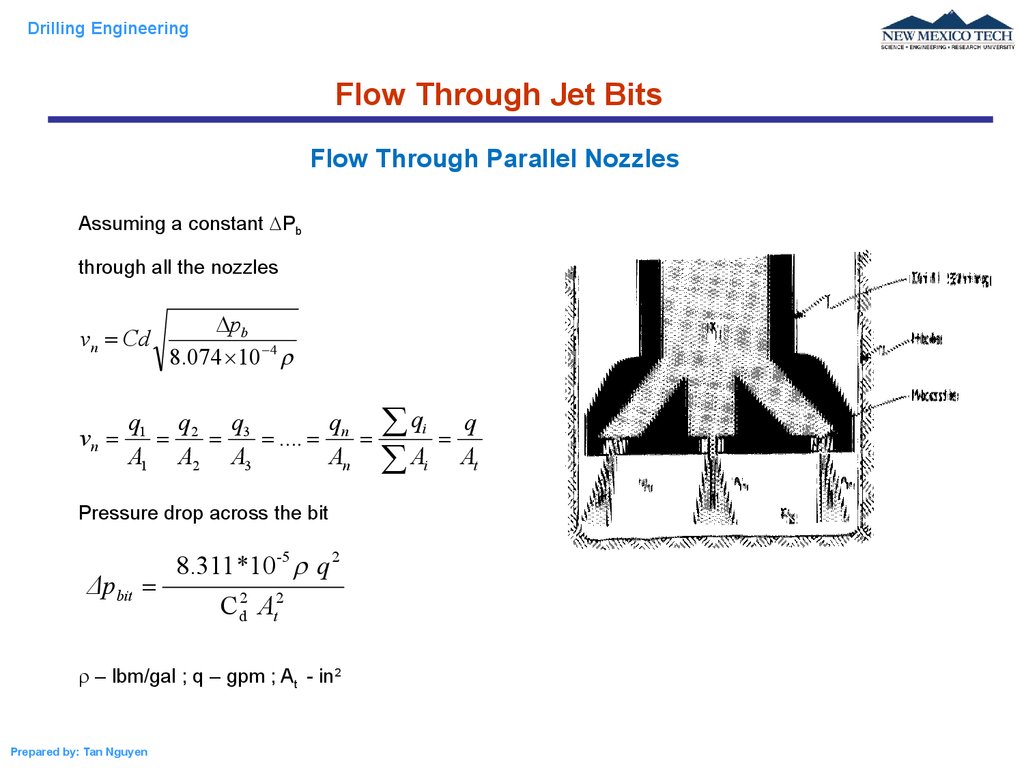
Drilling EngineeringFlow Through Jet Bits
Flow Through Parallel Nozzles
Assuming a constant Pb
through all the nozzles
vn Cd
vn
pb
8.074 10 4
q1 q2 q3
q
.... n
A1 A2 A3
An
Pressure drop across the bit
Δpbit
8.311 *10-5 q 2
C d2 At2
– lbm/gal ; q – gpm ; At - in2
Prepared by: Tan Nguyen
q
A
i
i
q
At
18.
Drilling EngineeringFlow Through Jet Bits
Hydraulic Impact Force
The purpose of the jet nozzles is to improve the cleaning action of the drilling fluid at the bottom of
the hole. Since the fluid is traveling at a vertical velocity v n , before reaching to the hole and
traveling at zero vertical velocity after striking the hole bottom hence all the fluid momentum is
transferred to the hole bottom.
Force is time rate of change of momentum, hence:
q vn
mv m
Fj
v
t
32.17 * 60
t
Substitute vn to the equation above gives
F j 0.01823 c d q p
Where Fj is the hydraulic impact force given in pounds.
Prepared by: Tan Nguyen
19.
Drilling EngineeringFlow Through Jet Bits
Flow Through Parallel Nozzles
Example: A 12.0 lbm/gal drilling fluid is flowing through a bit containing three 13/32 in nozzles at a
rate of 400 gal/min. Calculate the pressure drop across the bit and the impact force developed by
the bit.
Solution: Assume Cd = 0.95
2
13
At 3 0.3889in 2
4 32
Δpbit
8.311 *10 -5 q 2
C d2 At2
8.311 *10 5 *12 * 400 2
1169 psi
2
2
0.95 * 0.3889
Hydraulic impact force:
F j 0.01823 cd q p 0.01823 0.95 400 12 *1,169 820 lbf
Prepared by: Tan Nguyen
20.
Drilling EngineeringRheological Model
Flow curves of time-independent fluids
Prepared by: Tan Nguyen
Newtonian fluids:
Power law fluids:
K n
Bingham fluids:
y p
Herschel-Bulkley
(Yield power law fluids)
y K n
21.
Drilling EngineeringRheological Model
Newtonian Model
Non-Newtonian Model
Bingham-plastic model
p y ; y
0;
y y
p y ; y
Prepared by: Tan Nguyen
n
Power Law model:
K
Yield power law model:
y K
n
22.
Drilling EngineeringClassification of Drilling Fluids
Pseudoplastic
(Time-independent
shear thinning fluids)
If
the
apparent
viscosity
decreases with increasing shear
rate
Dilatant
(Time-independent
shear
thickening fluids)
If the apparent viscosity increases
with increasing shear rate
Flow curves of time-independent fluids
Prepared by: Tan Nguyen
23.
Drilling EngineeringClassification of Drilling Fluids
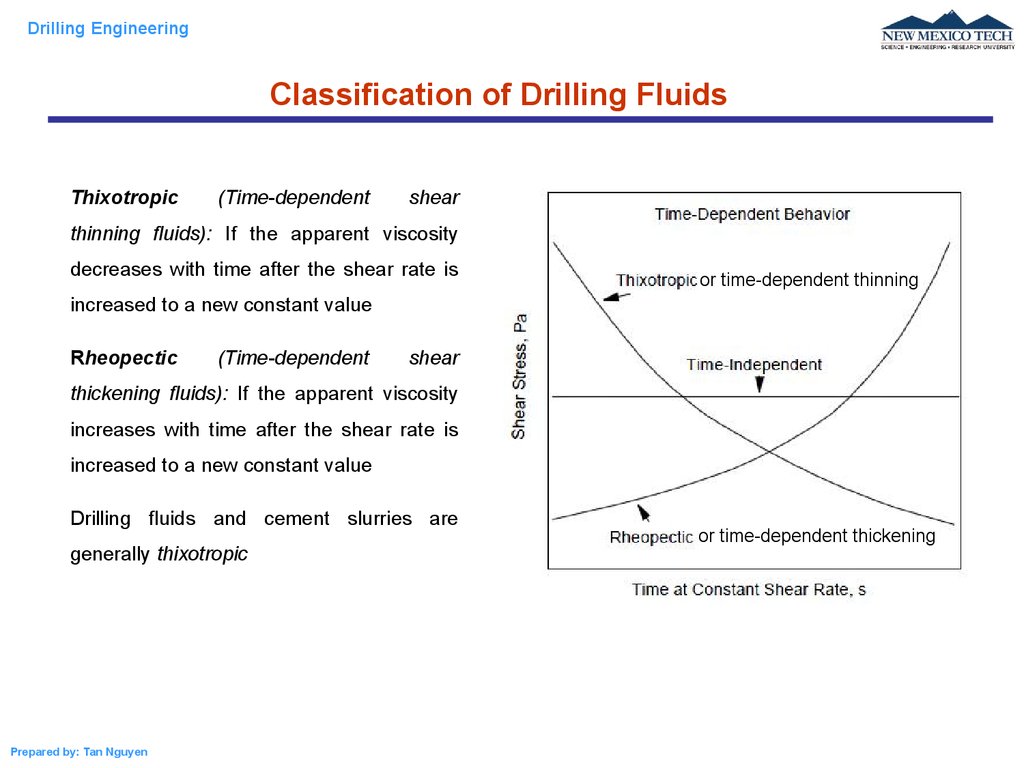
Thixotropic
(Time-dependent
shear
thinning fluids): If the apparent viscosity
decreases with time after the shear rate is
or time-dependent thinning
increased to a new constant value
Rheopectic
(Time-dependent
shear
thickening fluids): If the apparent viscosity
increases with time after the shear rate is
increased to a new constant value
Drilling fluids and cement slurries are
generally thixotropic
Prepared by: Tan Nguyen
or time-dependent thickening
24.
Drilling EngineeringRotational Viscometer
Prepared by: Tan Nguyen
25.
Drilling EngineeringRotational Viscometer
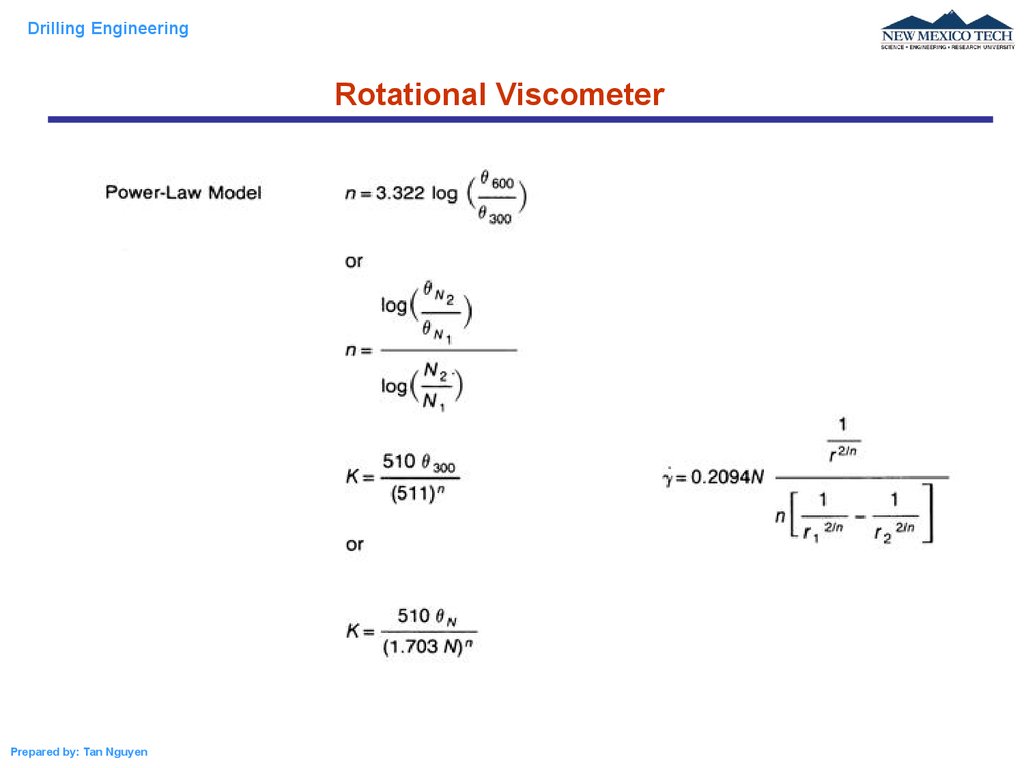
A rotational viscometer is used to determine type of the fluid and the rheological model of the
fluid. This can be done by varying the speed of the rotor (varying the shear rate) and reading the
dial reading (shear stress). To convert the speed to shear rate and dial reading to shear stress,
simply use these corellations:
= 1.703 x rpm, 1/s
= 1.06 x Dial Reading
Prepared by: Tan Nguyen
26.
Drilling EngineeringRotational Viscometer
Prepared by: Tan Nguyen
27.
Drilling EngineeringRotational Viscometer
Prepared by: Tan Nguyen
28.
Drilling EngineeringRotational Viscometer
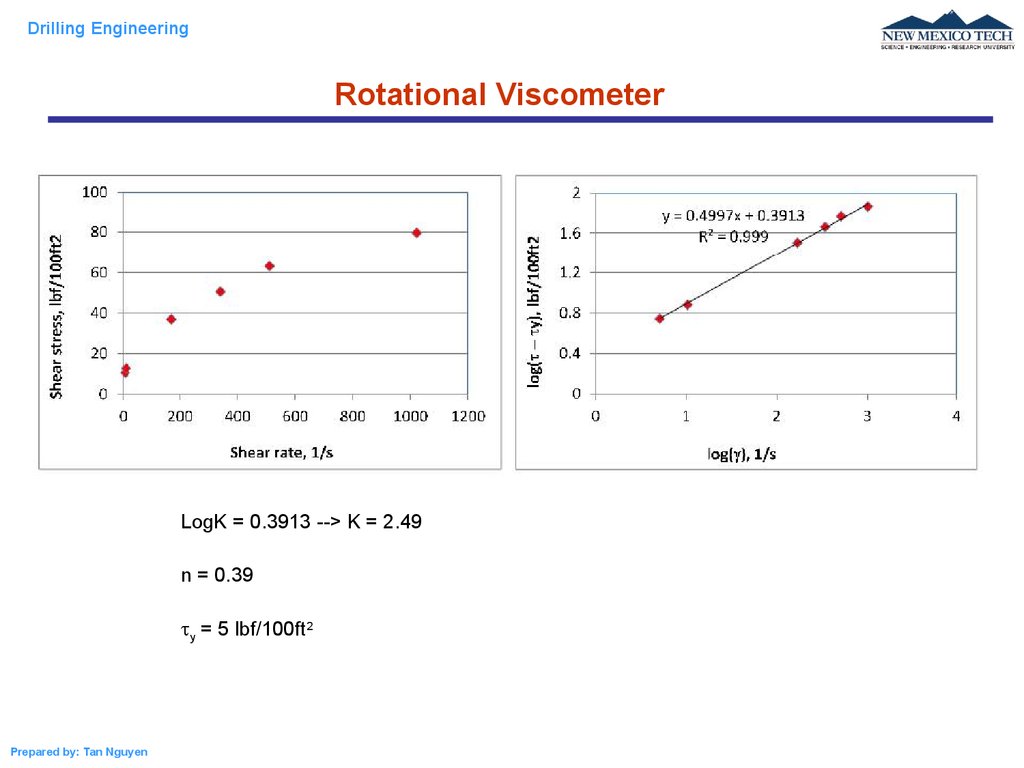
The data below are obtained from a rotational viscometer. Determine type of fluid and the
rheological model of this fluid.
Prepared by: Tan Nguyen
29.
Drilling EngineeringRotational Viscometer
LogK = 0.3913 --> K = 2.49
n = 0.39
y = 5 lbf/100ft2
Prepared by: Tan Nguyen
























 physics
physics








