Similar presentations:
Ортодромия и локсодромия. Ортодромическая поправка (лекция № 10)
1.
Федеральное государственное бюджетное образовательное учреждение высшего образованияКалининградский государственный технический университет
«Балтийская государственная академия рыбопромыслового флота»
(БГАРФ ФГБОУ ВО КГТУ)
Раздел 4. Картографические проекции и морские
навигационные карты.
Лекция № 10 (4.2)
Тема:
Калининград
2020
Доцент кафедры судовождения, кандидат военных наук,
доцент Щавелев В.П.
1
2.
Цель лекции. Учебные вопросыЦель лекции:
- формирование конвенционных компетентностей в части,
касающейся при движении судна по дуге большого круга при
ведении счисления с учетом ветра, приливов, течений и
рассчитанной скорости.
Учебные вопросы лекции:
1. Ортодромия.
2. Локсодромия.
3. Ортодромическая поправка.
2
3.
Литература3
Основная:
1. Дмитриев В.И, Рассукованый Л. С. Навигация и лоция, навигационная
гидрометеорология, электронная картография (+CD). Учебник. – Москва:
Моркнига, 2018 . – 312 с. - ISBN: 978-5-030033-52-5.
2. Дмитриев В.И., Григорян В.Л., Катенин В.А. Навигация и лоция. Учебник
для вузов (3-е издание переработанное и дополненное)/Под общ. Ред. д.ф.т.н.,
проф. В.И. Дектярева. – М.: «МОРКНИГА», 2009. – 458 с.: ил.
4.
Первый учебный вопрос1. Ортодромия.
4
5.
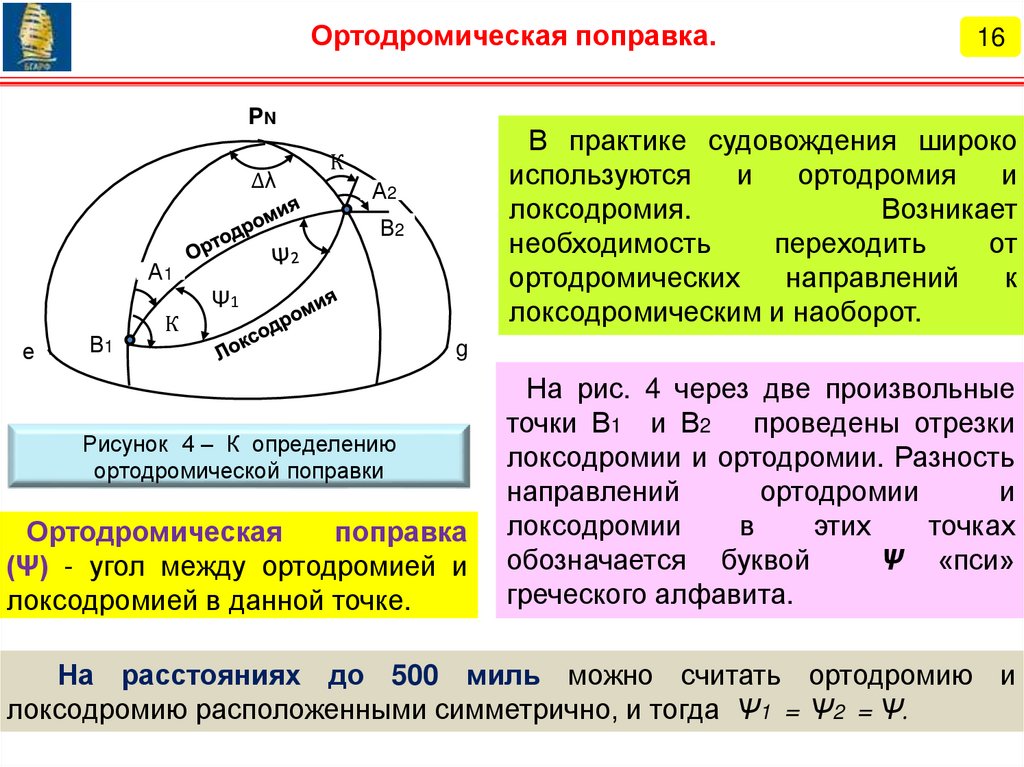
Ортодромия5
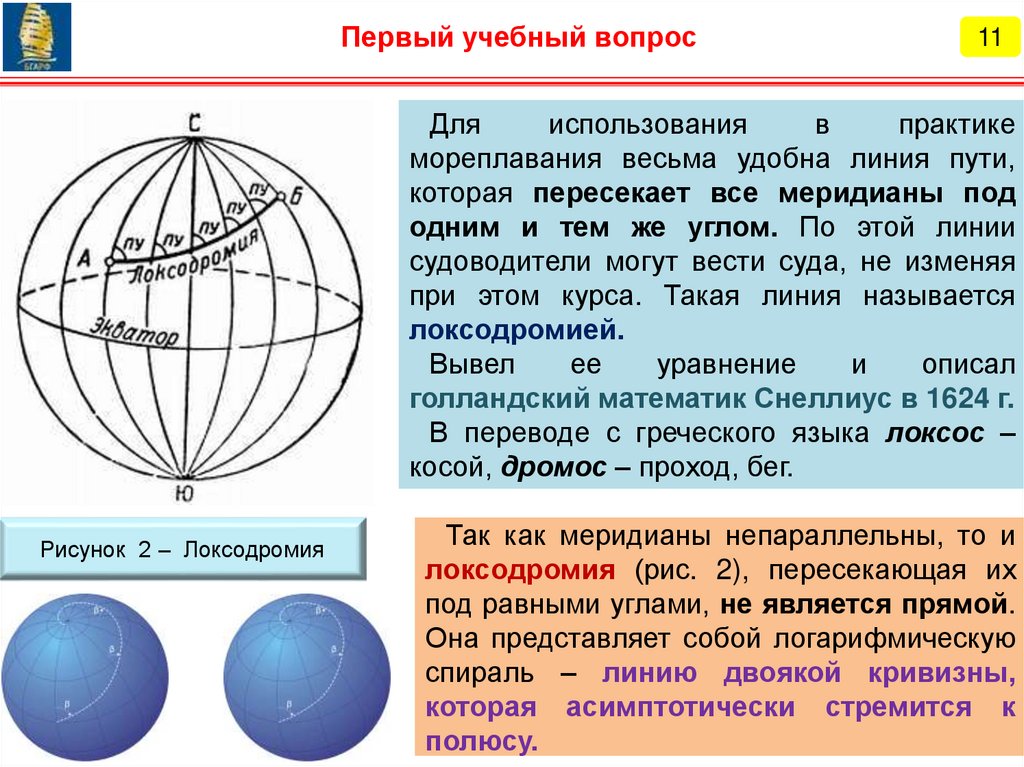
Одна из основных задач мореплавания в целом и навигации в
частности заключается в оптимизации путей судов. В общем случае
предпочтение отдается плаванию по кратчайшему расстоянию.
На эллипсоиде кратчайшим расстоянием между двумя точками
является геодезическая линия. Эта сложная линия двоякой кривизны
рассматривается в курсе высшей геодезии. Процесс ее расчета, прокладки
на карте, а тем более проводки по ней судов, достаточно трудоемкий.
На практике решение этой проблемы упрощают, рассматривая
кратчайшее расстояние между двумя точками на шаре. При
необходимости решения задач на эллипсоиде, пользуются поправками за
сфероидичность Земли, выбираемыми из специальных таблиц
(«Мореходные таблицы»).
На шаре линией кратчайшего расстояния является дуга большого
круга (ДБК), которую называют ортодромией. В переводе с греческого
языка ортос – прямой, дромос – проход, бег.
6.
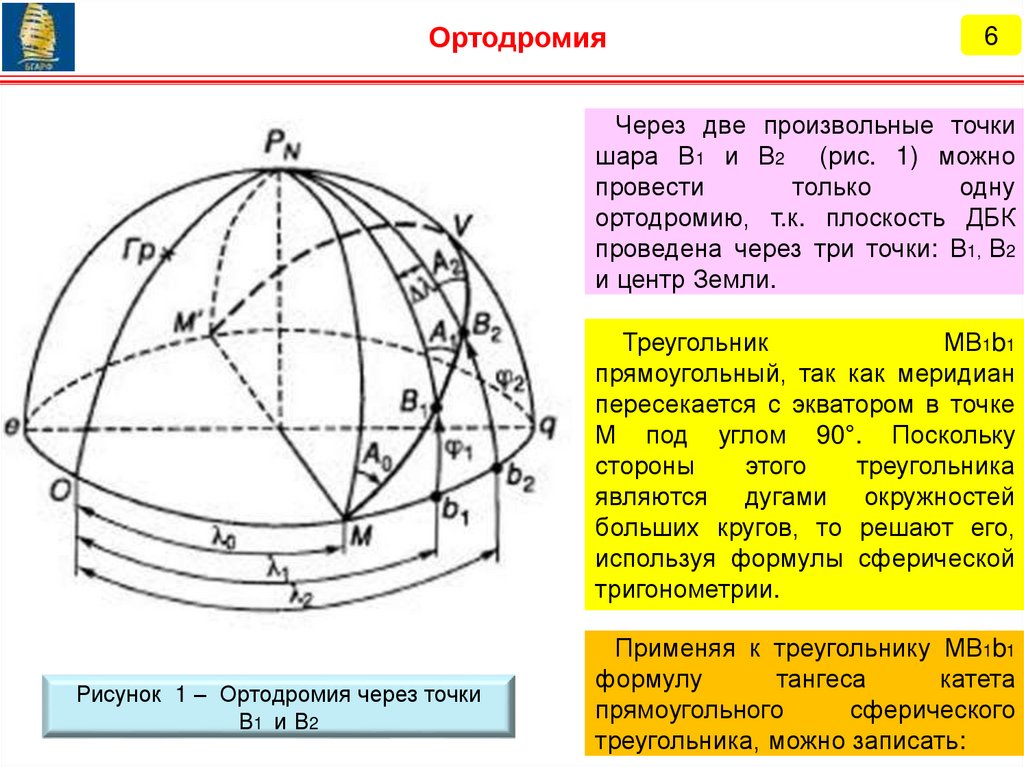
Ортодромия6
Через две произвольные точки
шара В1 и В2 (рис. 1) можно
провести
только
одну
ортодромию, т.к. плоскость ДБК
проведена через три точки: В1, В2
и центр Земли.
Треугольник
МВ1b1
прямоугольный, так как меридиан
пересекается с экватором в точке
М под углом 90°. Поскольку
стороны
этого
треугольника
являются дугами окружностей
больших кругов, то решают его,
используя формулы сферической
тригонометрии.
Рисунок 1 – Ортодромия через точки
В1 и В2
Применяя к треугольнику МВ1b1
формулу
тангеса
катета
прямоугольного
сферического
треугольника, можно записать:
7.
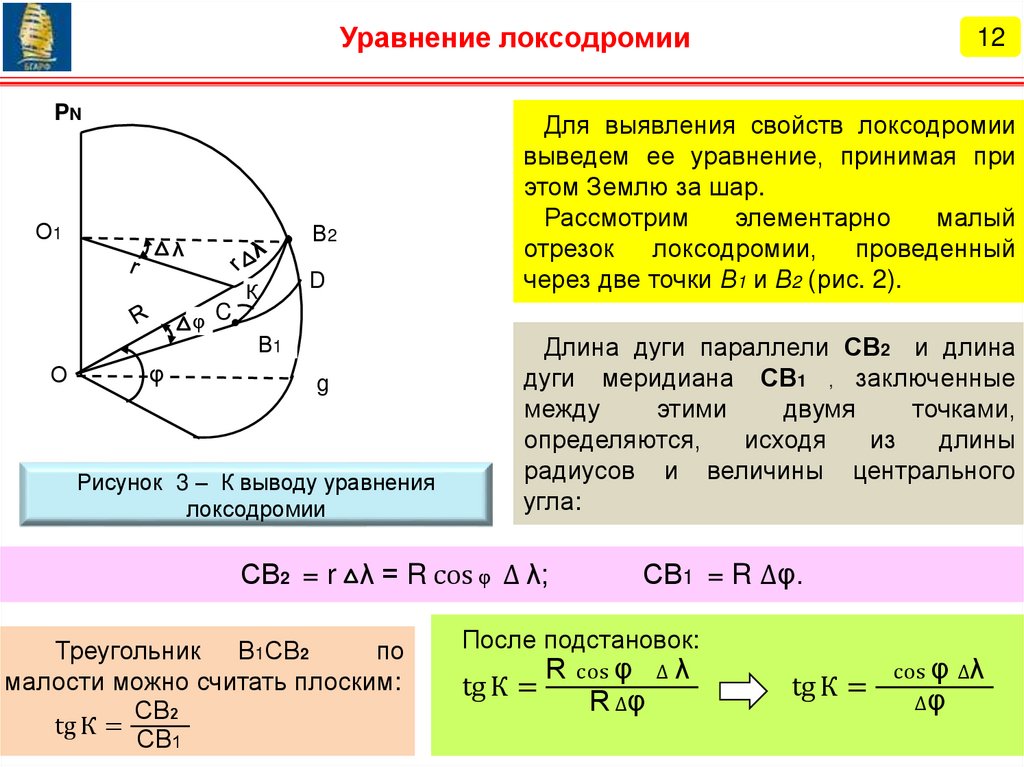
Ортодромия7
tg















 geography
geography