Навигация и лоция

1.

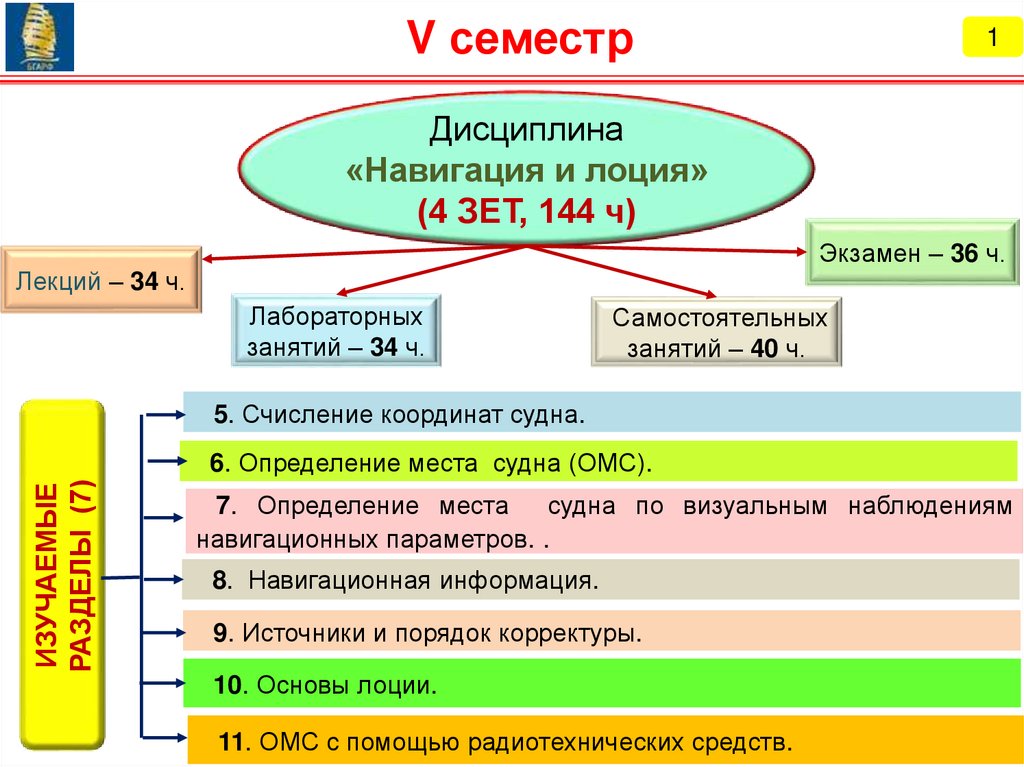
V семестр
1
Дисциплина
«Навигация и лоция»
(4 ЗЕТ, 144 ч)
Экзамен – 36 ч.
Лекций – 34 ч.
Лабораторных
занятий – 34 ч.
Самостоятельных
занятий – 40 ч.
5. Счисление координат судна.
ИЗУЧАЕМЫЕ
РАЗДЕЛЫ (7)
6. Определение места судна (ОМС).
7. Определение места
судна по визуальным наблюдениям
навигационных параметров. .
8. Навигационная информация.
9. Источники и порядок корректуры.
10. Основы лоции.
11. ОМС с помощью радиотехнических средств.

2.

V семестр
Формы контроля:
1. Текущий контроль:
- контрольный опрос;
- летучки;
- навигационные прокладки;
- Расчетно-графические работы (2):
1. РГР № 2 «Простое письменное счисление».
2. РГР № 3 «Составное письменное счисление».
2. Промежуточная аттестация – «ЭКЗАМЕН»
2

3.

Калининградский государственный технический университет
«Балтийская государственная академия рыбопромыслового флота»
Морской институт
Кафедра судовождения и безопасности мореплавания
Раздел 5 «Счисление координат судна»
Лекция № 1 (5.4 – Н.Р.)
Тема:
Калининград
2023
Доцент кафедры судовождения и безопасности мореплавания,
кандидат военных наук, доцент Щавелев В.П.
3

4.

Учебная цель лекции. Учебные вопросы.
Учебная цель:
- формирование конвенционных компетентностей в части,
касающейся аналитического счисления координат места судна с
учетом ветра, приливов, течений и расчета плавания по дуге
большого круга.
Учебные вопросы:
1. Основные формулы аналитического счисления.
2. Промежуточная широта, точная формула разности долгот.
4

5.

Литература
5
Основная:
1. Дмитриев В.И, Рассукованый Л. С. Навигация и лоция, навигационная
гидрометеорология, электронная картография (+CD). Учебник. – Москва: Моркнига,
2018 . – 312 с.
2. Дмитриев В.И., Григорян В.Л., Катенин В.А. Навигация и лоция. Учебник для
вузов (3-е издание переработанное и дополненное)/Под общ. ред. д.ф.т.н., проф.
В.И. Дмитриева. – М.: «МОРКНИГА», 2009. – 458 с.: ил.

6.

Первый учебный вопрос
1. Основные формулы аналитического счисления.
6

7.

Аналитическое счисление координат
7
Аналитическое счисление координат применяется в случаях, когда:
графическое счисление вести невозможно;
графическое счисление сопровождается значительными погрешностями.
Аналитическое счисление применяется:
- при океанских переходах, когда нет карт крупного масштаба и карт-сеток и,
следовательно,
графическое
счисление
сопровождается
значительными
погрешностями графических построений;
- когда графическое счисление вести невозможно из-за частых изменений
курса судна;
- при определении места по высотам Солнца, когда между наблюдениями
высот счисление должно быть максимально точным;
- во всех других случаях, когда необходимо повысить точность счисления пути
судна за счет исключения погрешностей графических построений.
Формулы аналитического счисления являются основой алгоритмов
автоматизированного счисления.
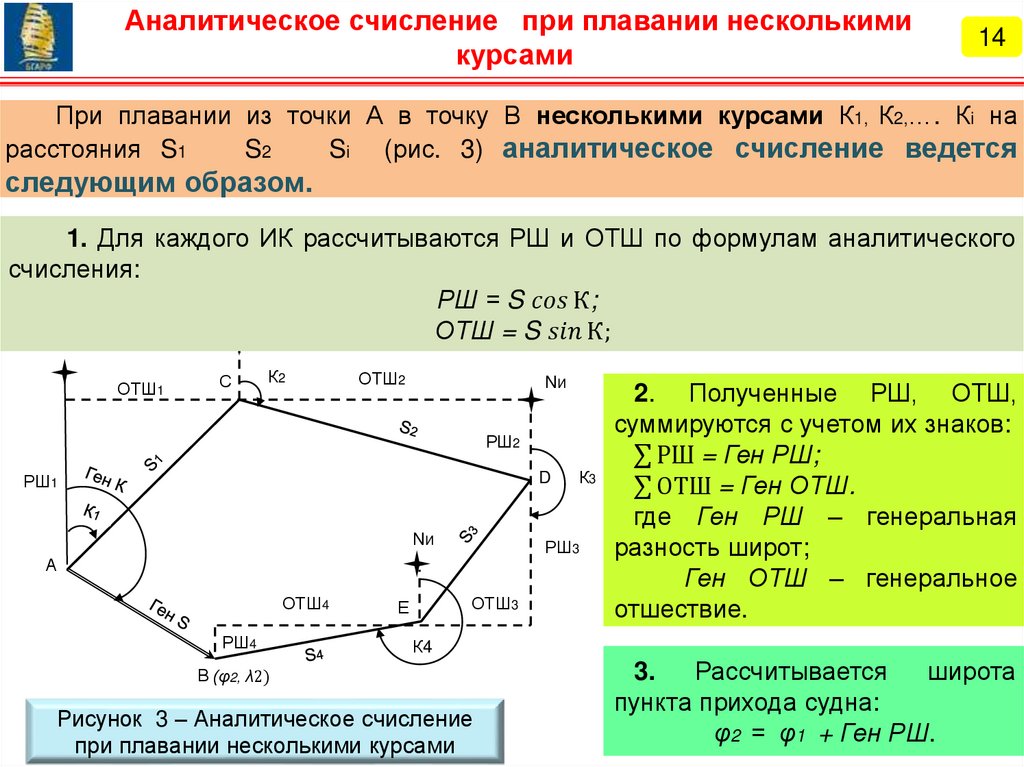
По формулам аналитического счисления рассчитываются:
истинный курс и расстояние по локсодромии для перехода судна из
исходной точки в заданную точку, координаты которой известны.

8.

Аналитическое счисление координат
8
Сущность аналитического счисления – расчет координат места судна
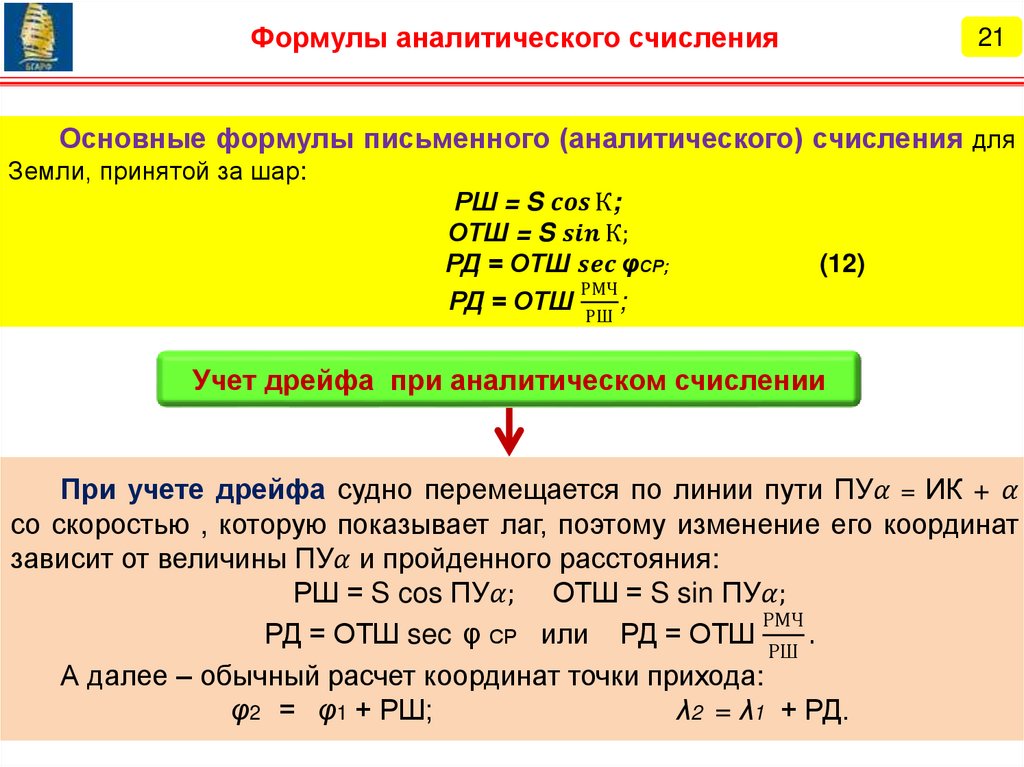
на заданный момент времени по известным формулам:
φ2 = φ1 + РШ,
λ2 = λ1 + РД.
Начальные координаты φ1
и λ1 всегда известны, поэтому задача
аналитического счисления сводится к расчету РШ и РД.
Для этого используются математические зависимости между изменениями:
- координат РШ и РД;
- истинным курсом ИК;
- плаванием (пройденным расстоянием) судна S.
РШ = f1 (ИК, S);
РД = f2 (ИК, S).
(1)
PN
i
t
f
D
l
с
φ К
А
a
d
В
h
g
D'
E
b
А'
b
Пусть судно из точки А с известными
координатами φ1 и λ1 совершило плавание
по локсодромии истинным курсом ИК = К,
прошло расстояние S и прибыло в точку В,
координаты которой φ2 и λ 2 необходимо
определить (рис.1).
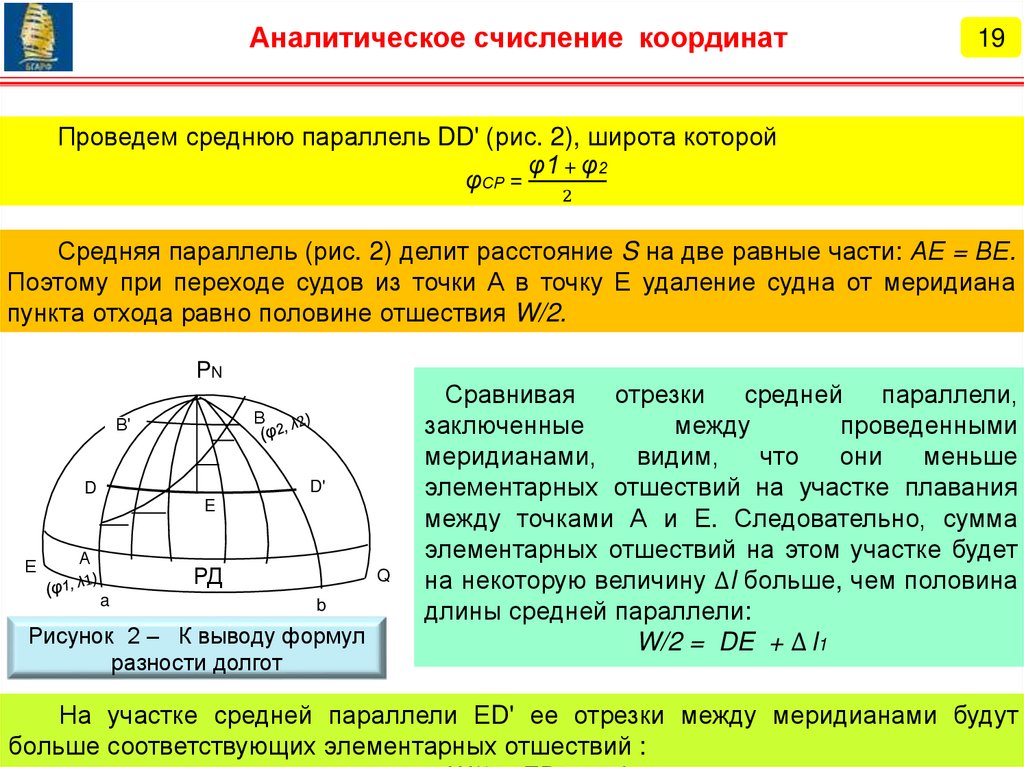
Рисунок 1 – К выводу формул
аналитического счисления

9.

Аналитическое счисление координат
9
Примем Землю за шар и разделим расстояние S на равные элементарные
отрезки ∆ S. Через полученные точки проведем меридианы и параллели. Получим
равные элементарные
прямоугольные треугольники. Гипотенузой каждого
треугольника является отрезок
∆ S, а катетами – отрезки меридианов и
параллелей. По малости сторон треугольники можно считать плоскими, и к ним
можно применять законы плоской тригонометрии.
В элементарном треугольнике Аbc:
- катет Ас является отрезком меридиана - т.е. элементарной
разностью широт ∆φ, которая определяется выражением:
∆ φ = ∆ S