Графический способ решения систем уравнений

1. Графический способ решения систем уравнений.

Учитель Каратанова М.Н.
Графический
способ решения
систем уравнений.
МОУ СОШ №256 г.Фокино.

2. Построение графика линейной функции.

Повторение
1.
Построение графика
линейной функции.
y = ах + b
х – любое действительное число
х
у
х1
у1
х2
у2

3. Построение графика функции обратной пропорциональности.

Повторение
2.
Построение графика функции
обратной пропорциональности.
у = k/x
1. х – любое
действительное число,
кроме нуля
2. Определить, в каких
четвертях находится
график функции.
k > 0 – I u III ч.
k < 0 – II u IV ч.
3. Составить таблицу
значений функции.

4.

3.
Повторение
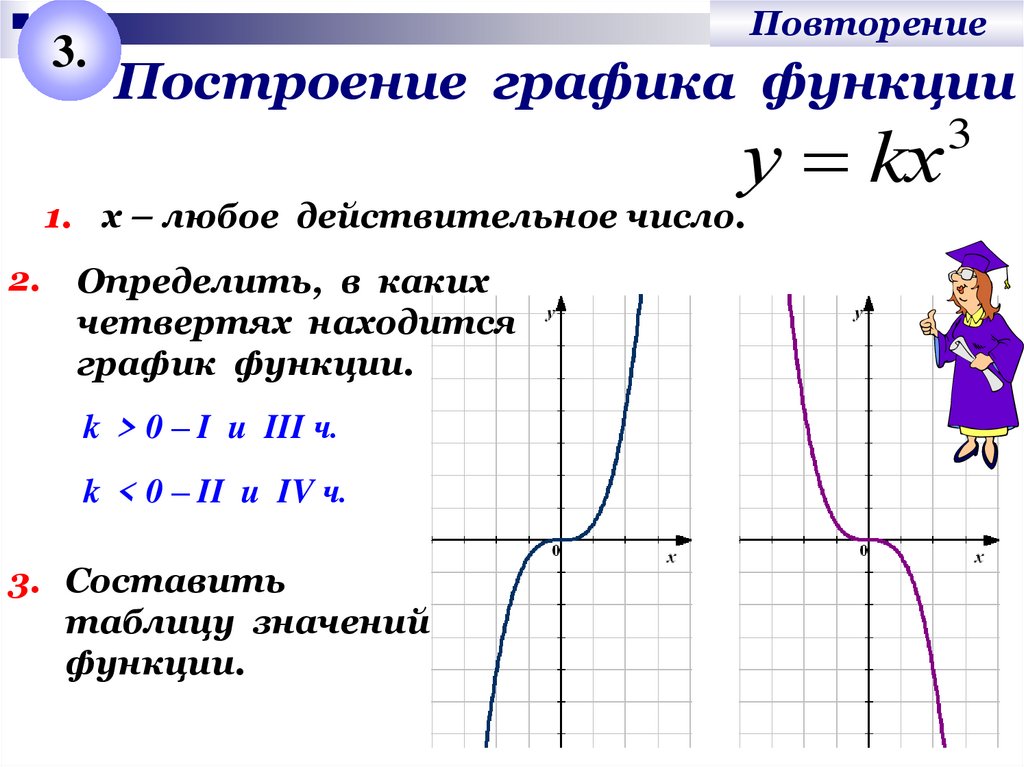
Построение графика функции
у kх
1. х – любое действительное число.
2.
Определить, в каких
четвертях находится
график функции.
k > 0 – I u III ч.
k < 0 – II u IV ч.
3. Составить
таблицу значений
функции.
3

5.

4.
Повторение
Построение окружности.
( х х0 ) ( у у0 ) r
2
2
r – радиус окружности.
(x0; у0 )– координаты
центра окружности.
2

6. Построение графика функции у = ах2 + bх +с.

5.
1.
Повторение
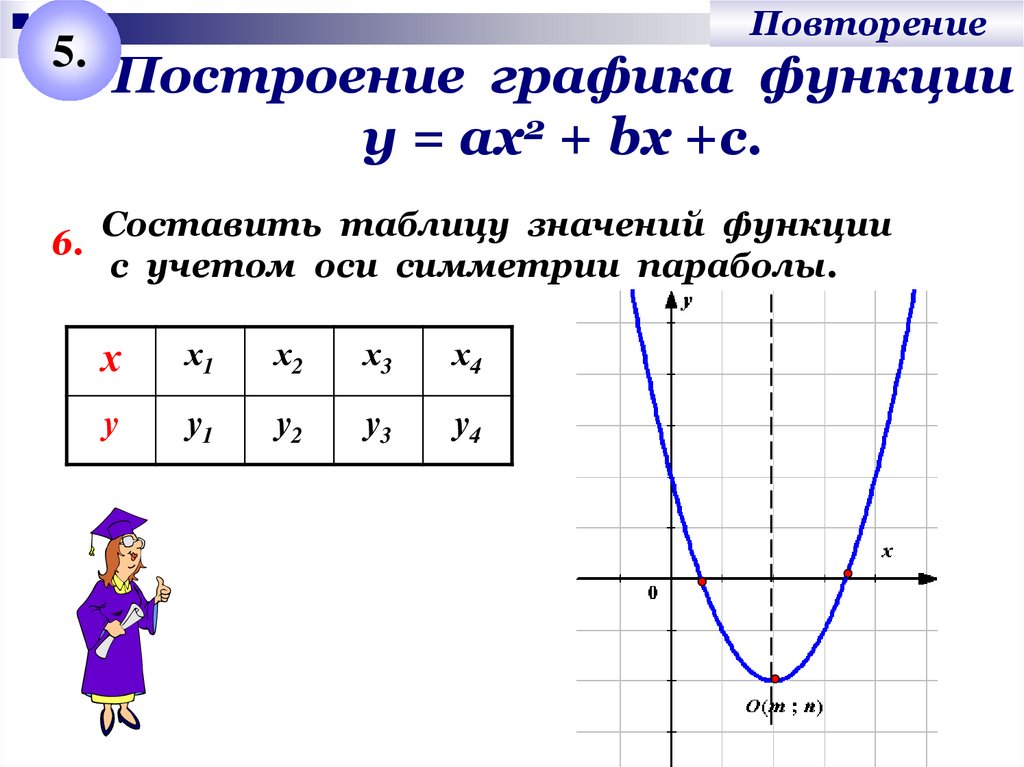
Построение графика функции
у = ах2 + bх +с.
х – любое действительное число.
2. Определить направление ветвей параболы.

7. Построение графика функции у = ах2 + bх +с.

5.
Повторение
Построение графика функции
у = ах2 + bх +с.
3. Найти координаты вершины параболы
(т; п).
b
т
2a
n y m
4. Провести ось
симметрии.
х т
О (т;п)

8. Построение графика функции у = ах2 + bх +с.

5.
Повторение
Построение графика функции
у = ах2 + bх +с.
Определить точки пересечения графика
5. функции с осью Ох, т.е. найти нули
функции.
у 0
ах bx c 0
2
(х1;0)
(х2;0)

9. Построение графика функции у = ах2 + bх +с.

5.
6.
Повторение
Построение графика функции
у = ах2 + bх +с.
Составить таблицу значений функции
с учетом оси симметрии параболы.
х
х1
х2
х3
х4
у
у1
у2
у3
у4

10.

Задание 1.
Решить графически y x 0
систему уравнений.
2
2 x y 3 0
1. y x 2
y 2x 3
2. Составим таблицы значений функций.
у х
2
у 2х 3
х -3 -2 -1 0
у 9 4 1 0
х
у
0 -3
3 -3
1
1
2
4
3
9
3. Построим графики
функций в одной
системе координат.

11.

Задание 1.
у х
х
у
2
-3 -2 -1
9 4 1
у 2х 3
0
0
х
у
1
1
2
4
3
9
В
0 -3
3 -3
А
Ответ: ( -1; 1); (3; 9)

12.

Задание 2.
Решить графически
систему уравнений.
1.
8
y
x
y x 3
yx 8
x y 3 0
2. Составим таблицы значений функций.
8
у
x
у х 3
х -8 -4 -2 -1 1
2
4
8
у
4
2
1
-1 -2 -4 -8 8
х 0 -3
у -3 0
3. Построим графики
функций в одной
системе координат.

13.

Задание 2.
х -8 -4 -2 -1 1
2
4
8
у
4
2
1
-1 -2 -4 -8 8
8
у
x
у х 3
х 0 -3
у -3 0
Ответ: решений нет

14.

Задание 3.
Решить графически
2
y x 4x 3
систему уравнений.
y 2 x 3
х 0 3
у 2 х 3
2
y
у 3 -3
x
2
у
x
х
-4
-2
-1
1
2
у
0,5
1
2
-2
-1 -0,5
у x 4х 3
2
Подробно
4

15.

у x 4х 3
2
1.
х – любое действительное число.
2. Графиком функции является парабола, ветви
которой направлены вверх. a > 0
3. Найдём координаты вершины параболы
b
х0
2a
4.
ó x2 4õ 3
4
х0 2
2
у0 2 4 2 3 1
2
М ( 2; -1)
Дополнительные точки:
х
0
1
2
3
4
5
у
3
0
-1
0
3
8

16.

у x 4х 3
2
2
у
x
М
у 2 х 3
Ответ: ( 2; -1)

17.

Самостоятельно.
Решить графически
систему уравнений.
x у 25
2
y х 6
2
2
Проверка (2)
Ответ: ( -3; 4); (3; 4);
(-1; 4,9); (1; 4,9)

18.

Самостоятельно.
Решить графически
систему уравнений.
у х
yх 12
3
Проверка (2)
Ответ: решений нет

19.

Самостоятельно.
Решить графически
систему уравнений.
у 2 х
3
0,5 х у 0
Проверка (2)
Ответ: (2; 4)

20. Домашнее задание

Изучить п. 17 учебника
Решить графически систему уравнений
1) а) х = -1;
х2 + у = 4;
б) х у = 3;
2х – у = 2;
в) х2 + у2 = 4;
у = х2 – 2.