Similar presentations:
Свойства прямоугольных треугольников. 7 класс
1. Двенадцатое января Классная работа Свойства прямоугольных треугольников
2.
ТРЕУГОЛЬНИК-геометрическая фигура,
состоящая из трёх точек,
не лежащих на одной
прямой и соединённых
отрезками, называется
3. Прямоугольный треугольник
Если один изуглов
треугольника
прямой, то
треугольник
называется
прямоугольным.
4.
Сумма двух острых углов прямоугольноготреугольника равна 90°
Доказательство:
Сумма углов треугольника равна
180° , а прямой угол равен 90° ,
поэтому сумма двух острых углов
прямоугольного треугольника равна
90° .
5.
Катет прямоугольного треугольника ,лежащий против угла в 30°, равен половине
гипотенузы.
Рассмотрим прямоугольный треугольник,
В
в котором A -прямой, B =30° и значит, C=60°.
Докажем, что AC =1 2 BC.
Доказательство:
30° 30°
60°
D
Приложим к треугольнику АВС равный
ему треугольник АВD.
60°
С Получим треугольник ВСD, в котором
А
В= D=60°, поэтому DС=ВС. Но
АС=1 2 DС. Следовательно, AC =1 2 BC,
что и требовалось доказать.
6.
Если катет прямоугольного треугольникаравен половине гипотенузы, то угол,
лежащий против этого катета, равен 30°.
В
Доказательство:
Рассмотрим прямоугольный треугольник,
у которого катет АС равен половине
гипотенузы ВС.
Докажем, что АВС=30°
D
А
С
Приложим к треугольнику АВС равный
ему треугольник АВD.
Получим равносторонний треугольник ВСD.
Углы равностороннего треугольника равны
друг другу, поэтому каждый из них равен 60°
В частности, DBС=60°. Но DВС=2 АВС
Следовательно, АВС=30°, что и
требовалось доказать.
7. Свойство 4
Теорема В прямоугольномтреугольнике гипотенуза больше
катета
Доказательство
Каждый из катетов лежит против
острого угла, а гипотенуза – против
прямого угла. Прямой угол больше
острого, следовательно,
гипотенуза больше катета
8. Свойство 5
9.
ВНайти:
угол В
37 0
С
А
10.
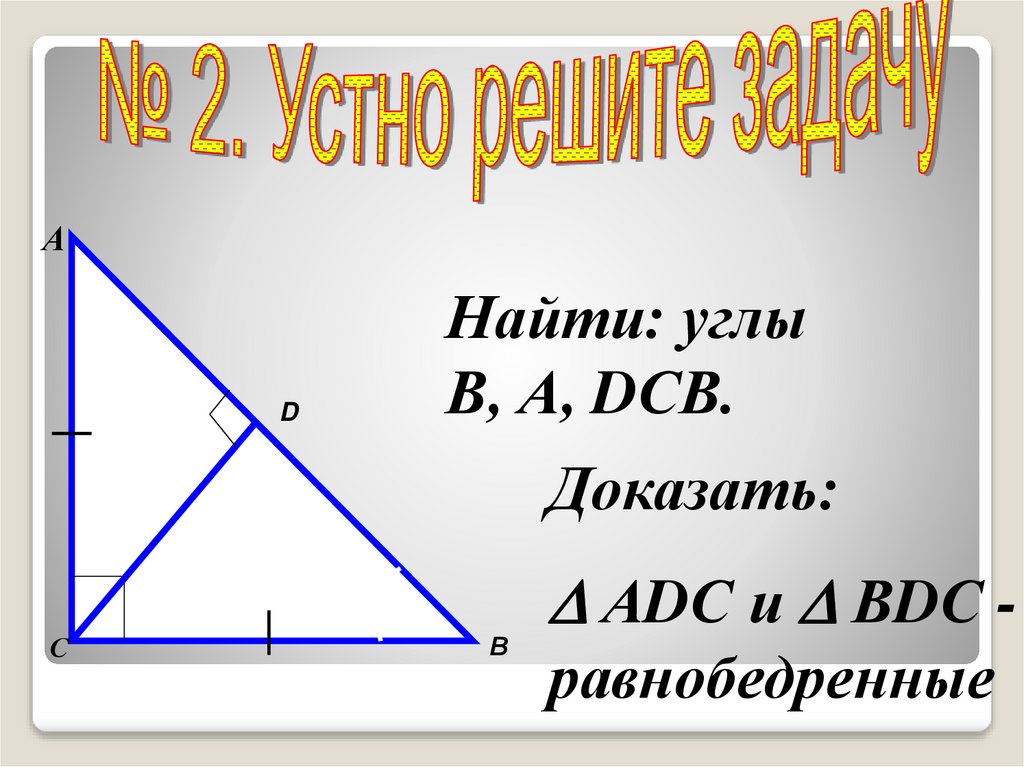
АD
Найти: углы
В, А, DСВ.
Доказать:
С
В
АDС и ВDС равнобедренные
11.
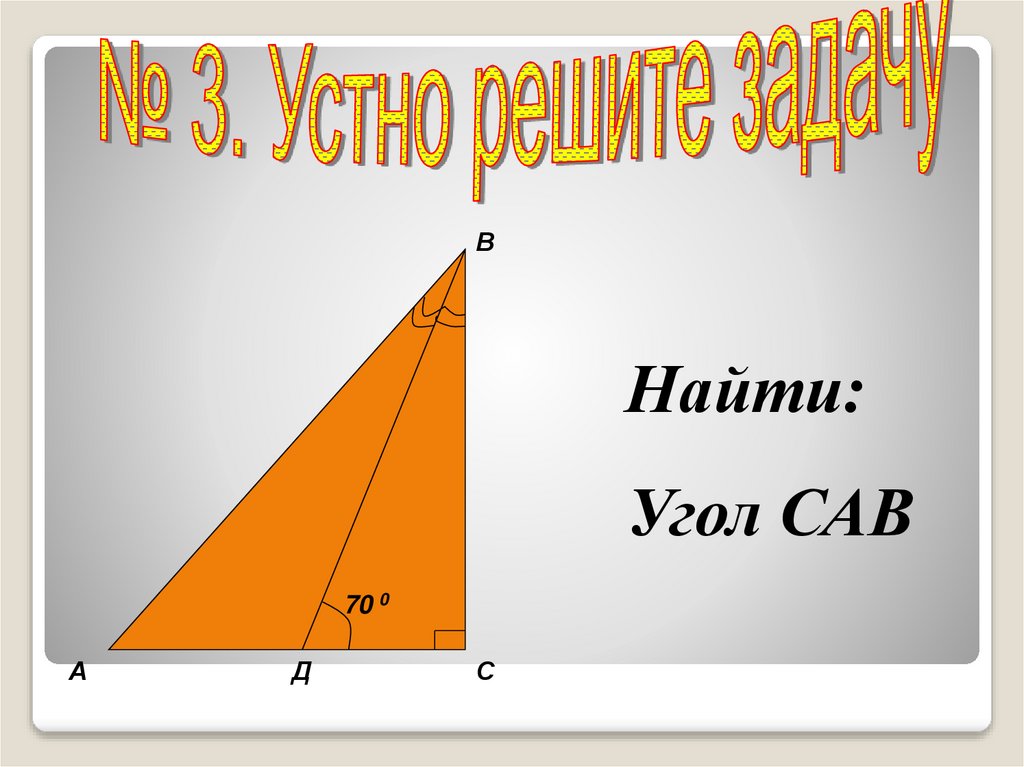
ВНайти:
Угол САВ
70 0
А
Д
С
12.
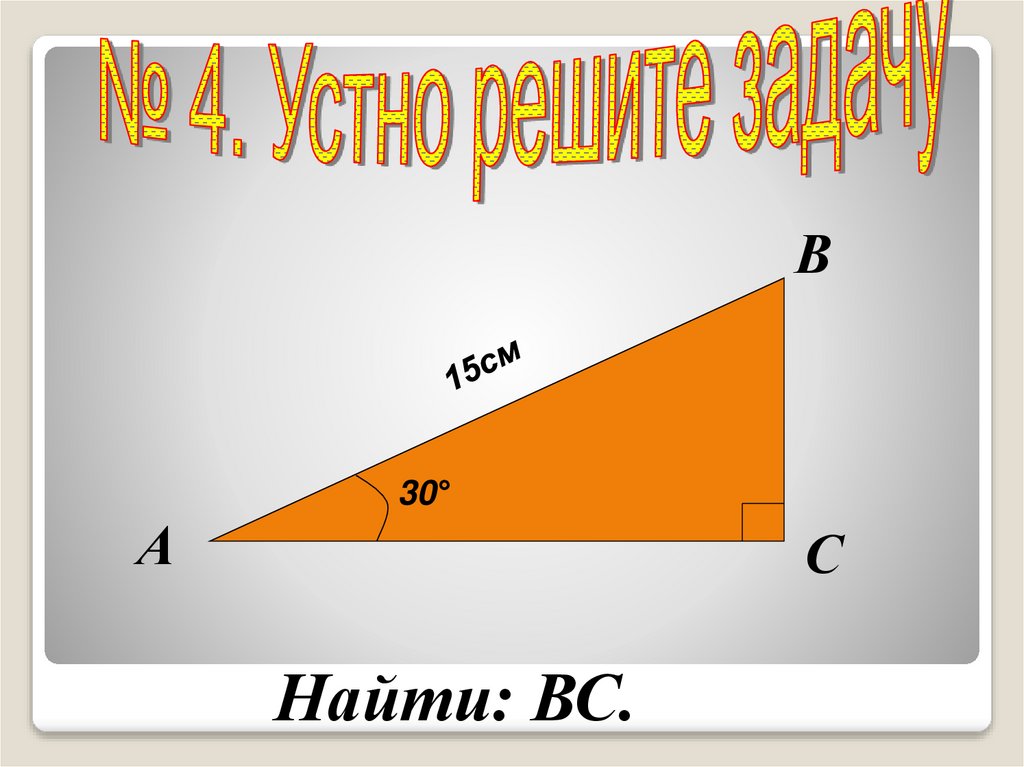
В30°
А
С
Найти: ВС.
13.
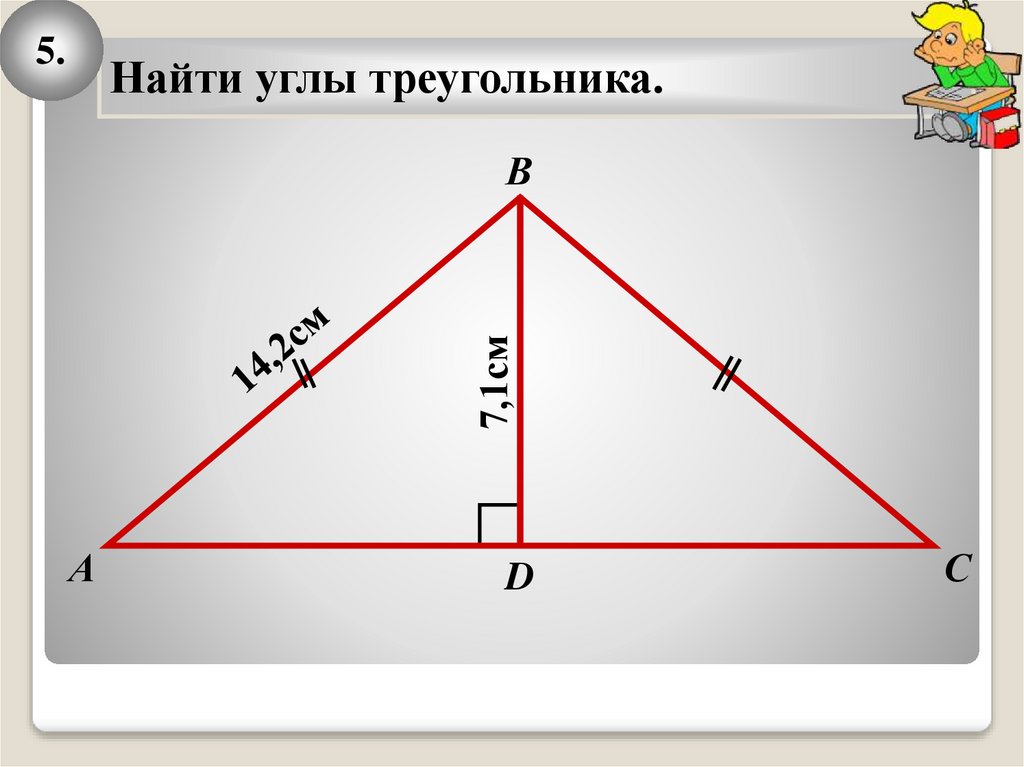
5.Найти углы треугольника.
7,1см
В
А
D
С
14.
Домашнее заданиеВыучить: п.35,
Выполнить: №256










 mathematics
mathematics








