Начертательная геометрия. Лекция 1. Проекции точки

1.

2.

Рекомендуемая литература
• Начертательная геометрия Учеб. для вузов / Н. Н. Крылов, Г. С. Иконникова,
В. JI. Николаев, В. Е. Васильев ; под ред. Н. Н. Крылова. — 8-е изд., испр. —
М.: Высш. шк., 2002. — 224 с.: ил.
Для студентов строительных специальностей вузов
• Гордон В. О. Курс начертательной геометрии : учеб. Пособие для втузов /
В. О. Гордон, М. А. Семенцов-Огиевский; под ред. Ю. Б. Иванова. – М.:
Наука, 1988, 1989, 2000.
• Фролов С. А. Начертательная геометрия / С. А. Фролов. – 2-е изд. – М.:
Машиностроение, 1983.
• Начертательная геометрия в примерах и задачах /О.Н.Леонова,
Е.А.Разумнова, - 2018,Лань

3.

Moodle
Программы дополнительного образования
Дистанционное обучение
Портал дистанционного обучения СПбГАСУ
Кафедры
Начертательной геометрии и инженерной графики
пароль ingraf

4.

ЛЕКЦИЯ №1
ПРОЕКЦИИ ТОЧКИ

5.

Начертательная геометрия –излагает
способы построения пространственных форм
на
плоскости
геометрического
изображениям.
и
учит
решать
характера
по
задачи
заданным

6.

Исторические сведения

7.

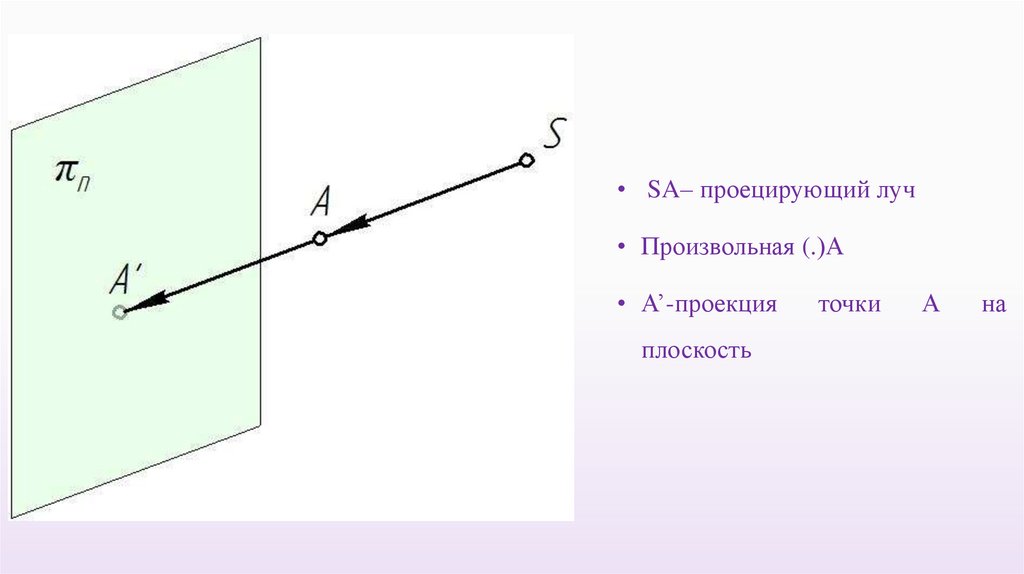
Проецирование — это процесс, в результате которого получают изображения,
представляющие собой проекции на плоскости.
Аппарат проецирования
πn – плоскость
проекций
S – центр
проецирования

8.

• SA– проецирующий луч
• Произвольная (.)А
• А’-проекция
плоскость
точки
А
на

9.

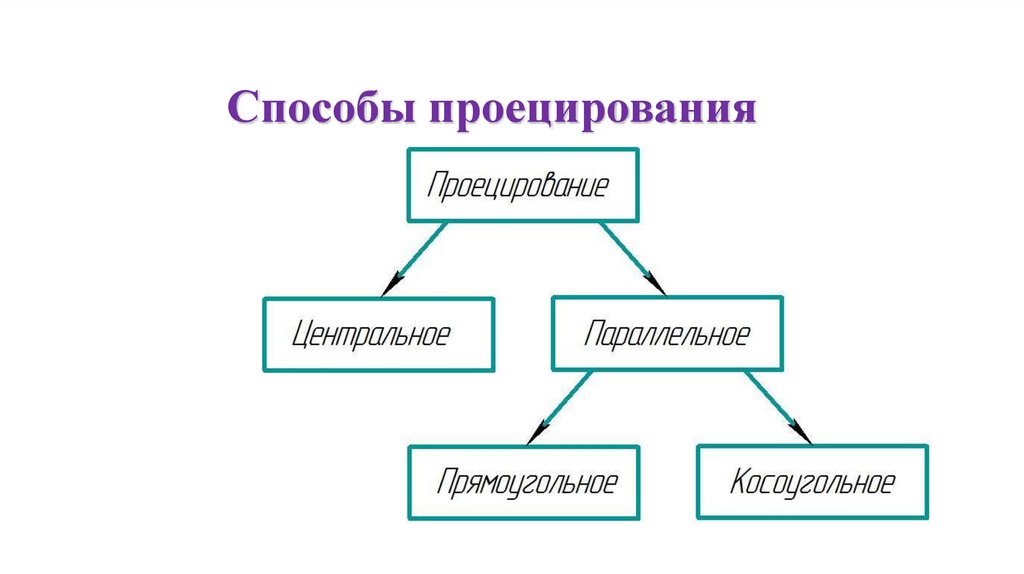
Способы проецирования

10.

Центральное проецирование
(коническое)
S (центр проецирования) -–
реальная точка.
Пn-плоскость проекций
А,В,С- точки в пространстве
А',В',С'-проекции точек на
плоскость
Проекцией точки на
плоскость называют точку
пересечения проецирующего
луча с плоскостью проекций

11.

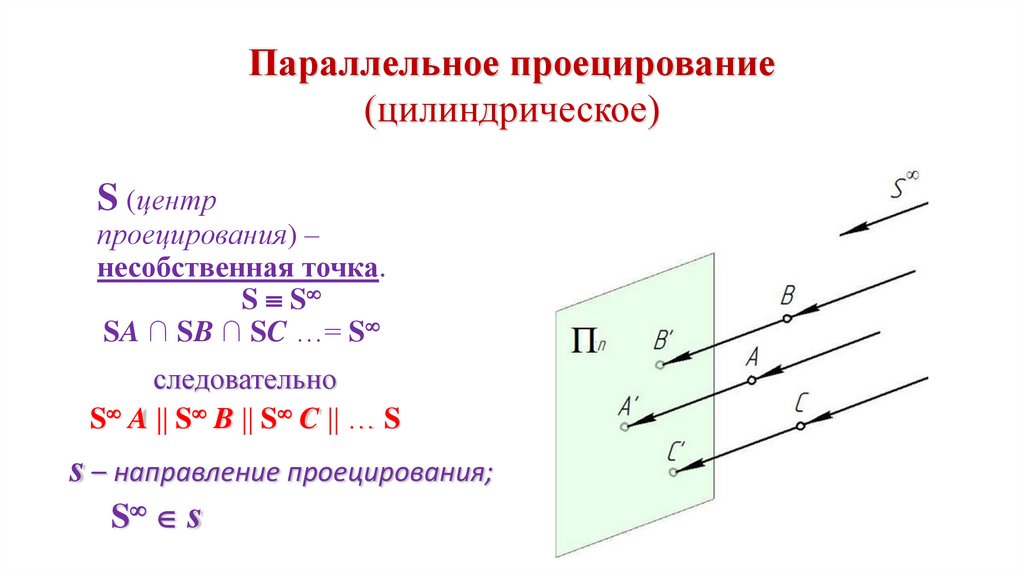
Параллельное проецирование
(цилиндрическое)
S (центр
проецирования) –
несобственная точка.
S S
SA ∩ SB ∩ SC …= S
следовательно
S A S B S C … S
s – направление проецирования;
S s

12.

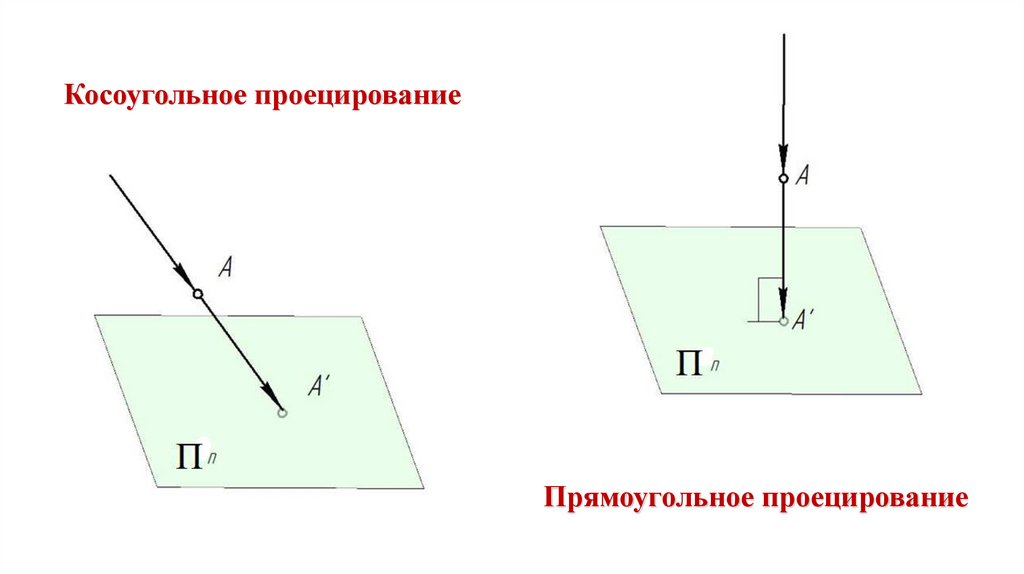
13.

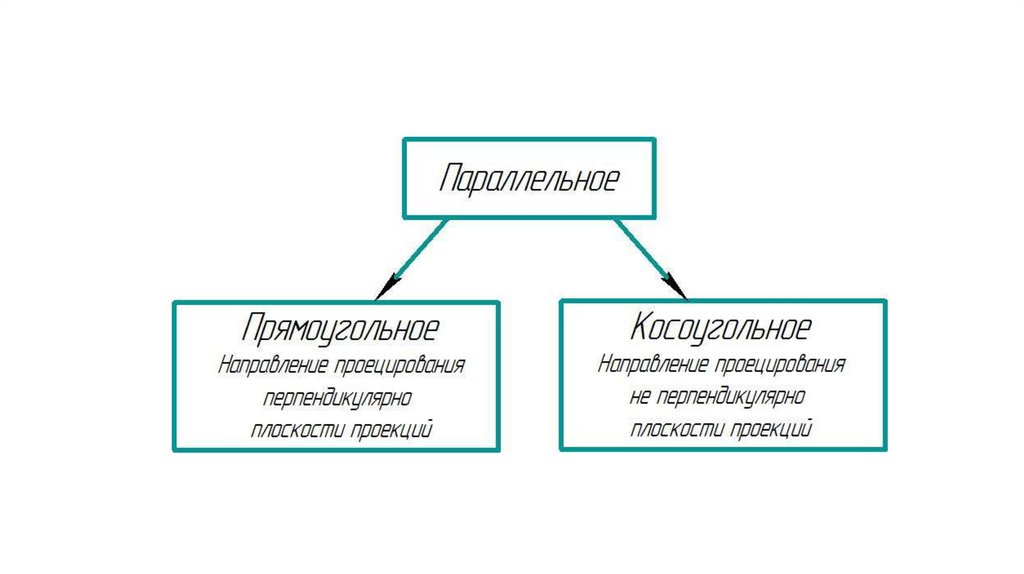
Косоугольное проецирование
Прямоугольное проецирование

14.

Метод Монжа
Ортогональная система двух
взаимно перпендикулярных
плоскостей проекций

15.

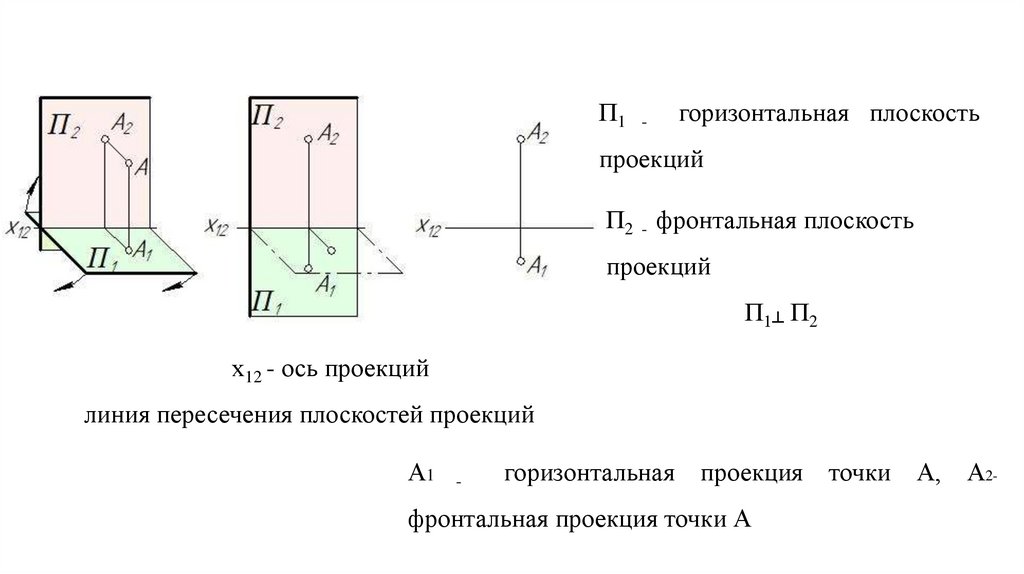
П1 -
горизонтальная плоскость
проекций
П2 - фронтальная плоскость
проекций
П1┴ П2
х12 - ось проекций
линия пересечения плоскостей проекций
А1
-
горизонтальная проекция точки А, А2-
фронтальная проекция точки А

16.

Положение 1.Плоскости считаются бесконечными
и непрозрачными
Положение 2.
Ортогональные проекции точки на две взаимно перпендикулярные плоскости вполне определяют
положение этой точки в пространстве.
Положение 3.
Проекции одной точки расположены на одном перпендикуляре к оси проекций.Этот перпендикуляр
называется линией проекционной связи.
Положение 4.
Развернутое положение плоскостей проекций с проекциями точки на них называется э пю р о м .

17.

Ортогональная система
трёх плоскостей проекций

18.

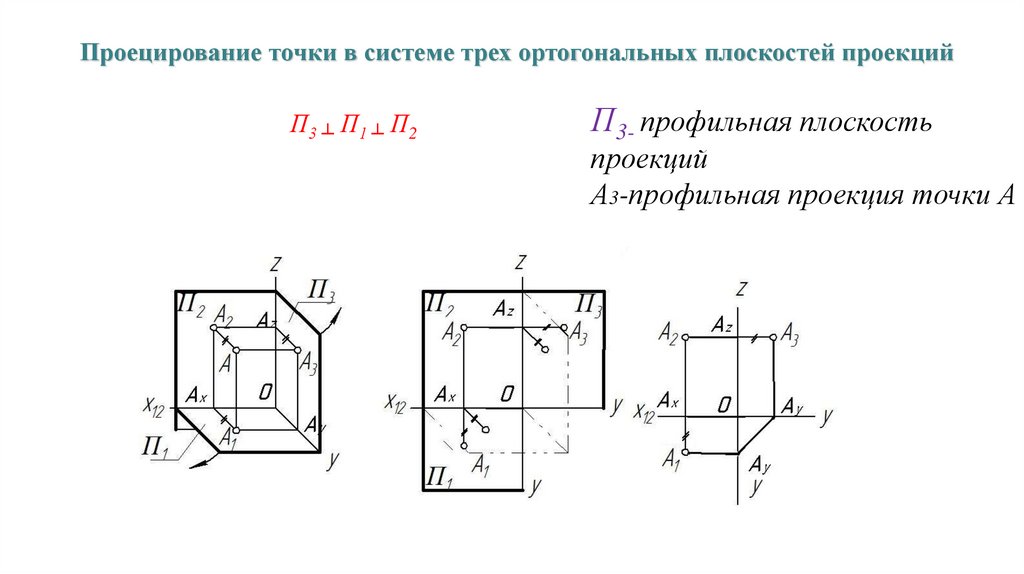
Проецирование точки в системе трех ортогональных плоскостей проекций
П3 ┴ П1 ┴ П2
П3- профильная плоскость
проекций
А3-профильная проекция точки А

19.

Две проекции точки располагаются на одной линии связи.
Линии связи всегда перпендикулярны осям проекций.
По двум любым проекциям всегда можно построить третью проекцию
точки..

20.

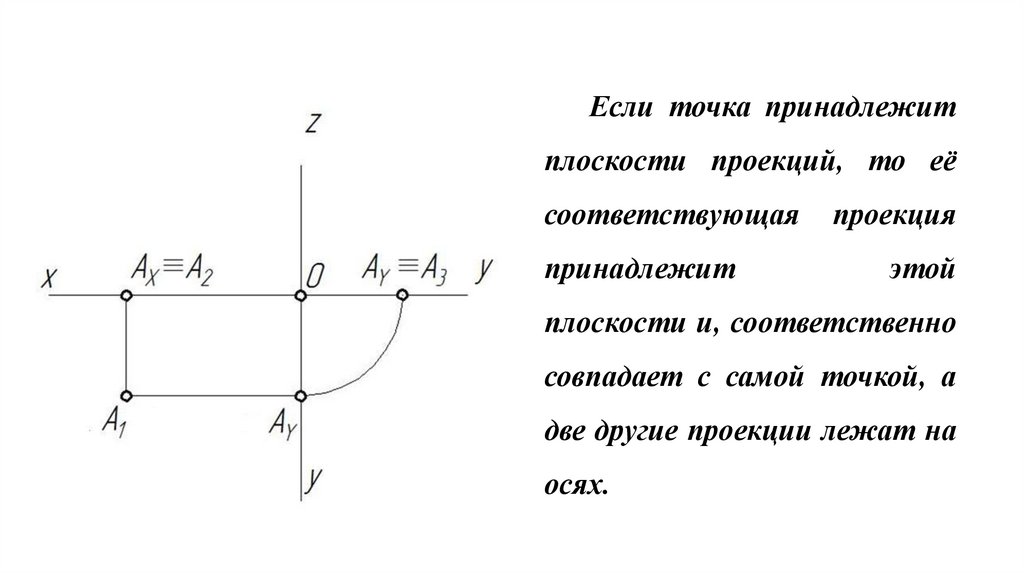
Если точка принадлежит
плоскости проекций, то её
соответствующая
принадлежит
проекция
этой
плоскости и, соответственно
совпадает с самой точкой, а
две другие проекции лежат на
осях.

21.

Переход к безосному чертеж
Существует безосный эпюр . Его применяют, если нет необходимости в
определении положения точки (или других геометрических элементов)
относительно плоскостей проекций.

22.

Четверти пространства
Две взаимно перпендикулярные плоскости делят
пространство на 4 двугранных угла ,называемых четвертями

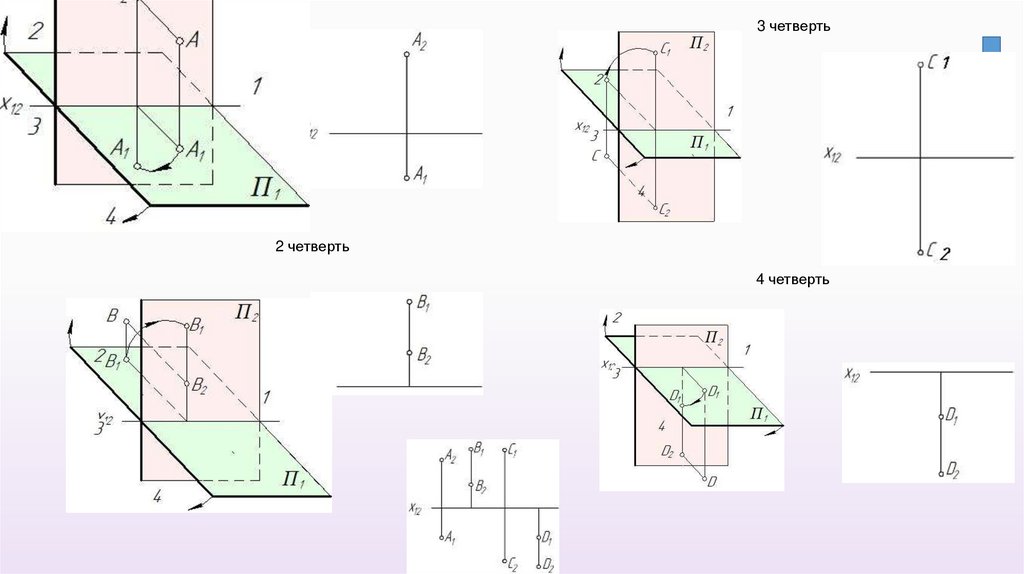
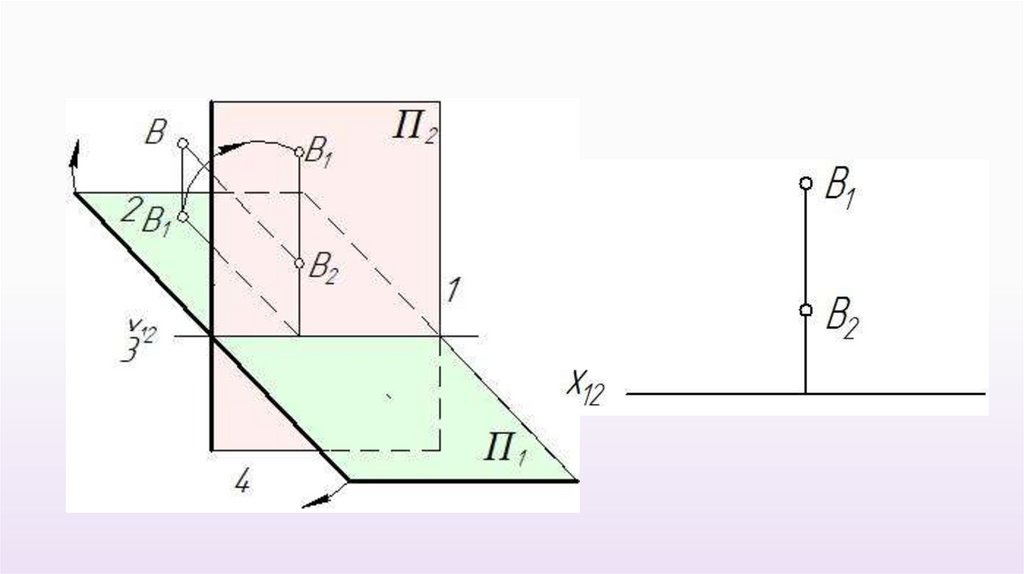
23.

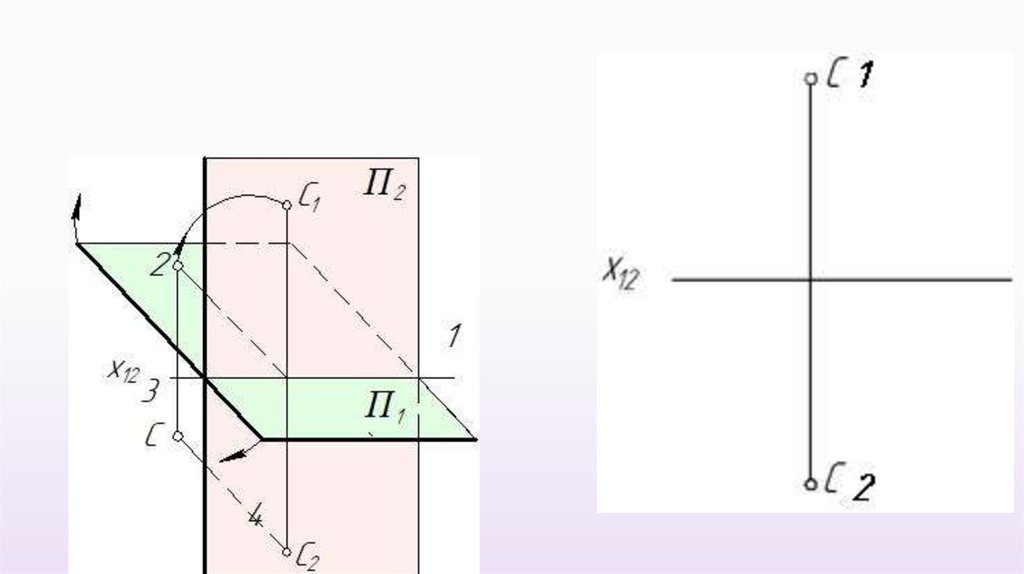
1 четверть
3 четверть
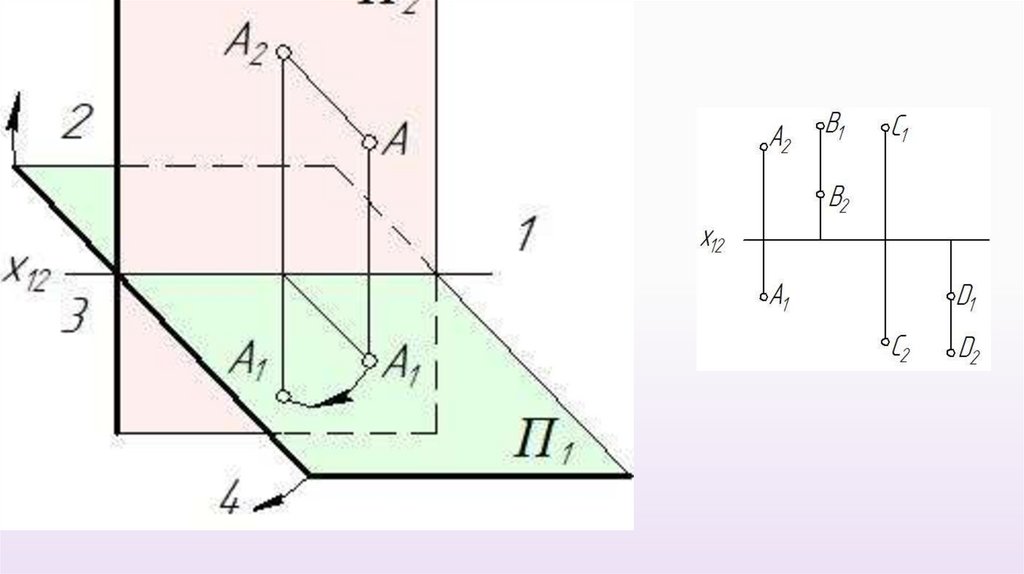
2 четверть
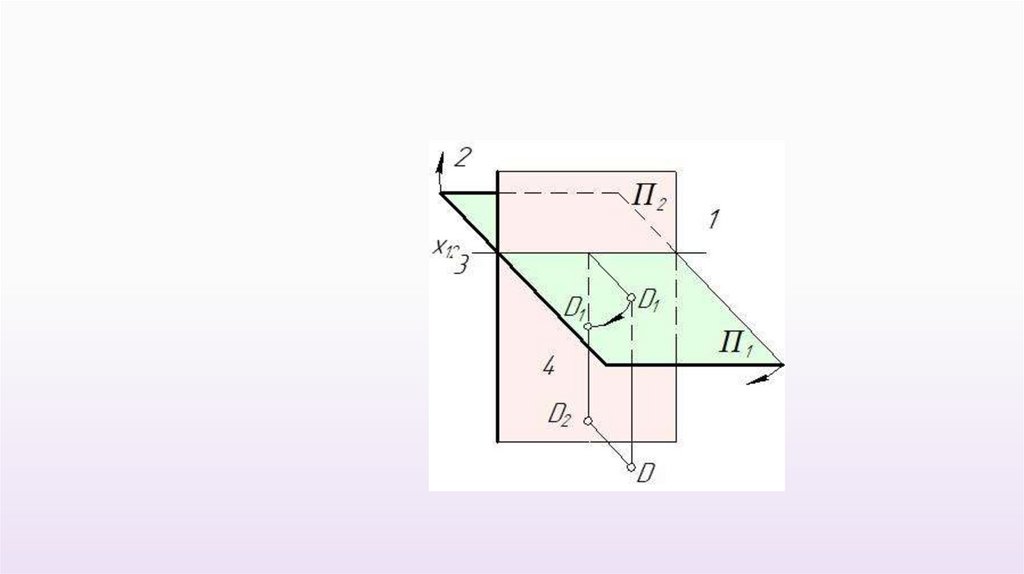
4 четверть