Двугранный угол

1.

Домашняя работа за 11.01.
Запись в тетради:
11.01. ДВУГРАННЫЙ УГОЛ
1) Изучить теоретический материал из презентации+ видеоурок
по ссылке https://disk.yandex.ru/i/dtW_QBnbWJiRGg + при
необходимости (если недостаточно информации) учебник
геометрии п.22,23 .
2) Решить в тетради задачи №170, №6 из презентации.

2.

11.01. ДВУГРАННЫЙ УГОЛ

3.

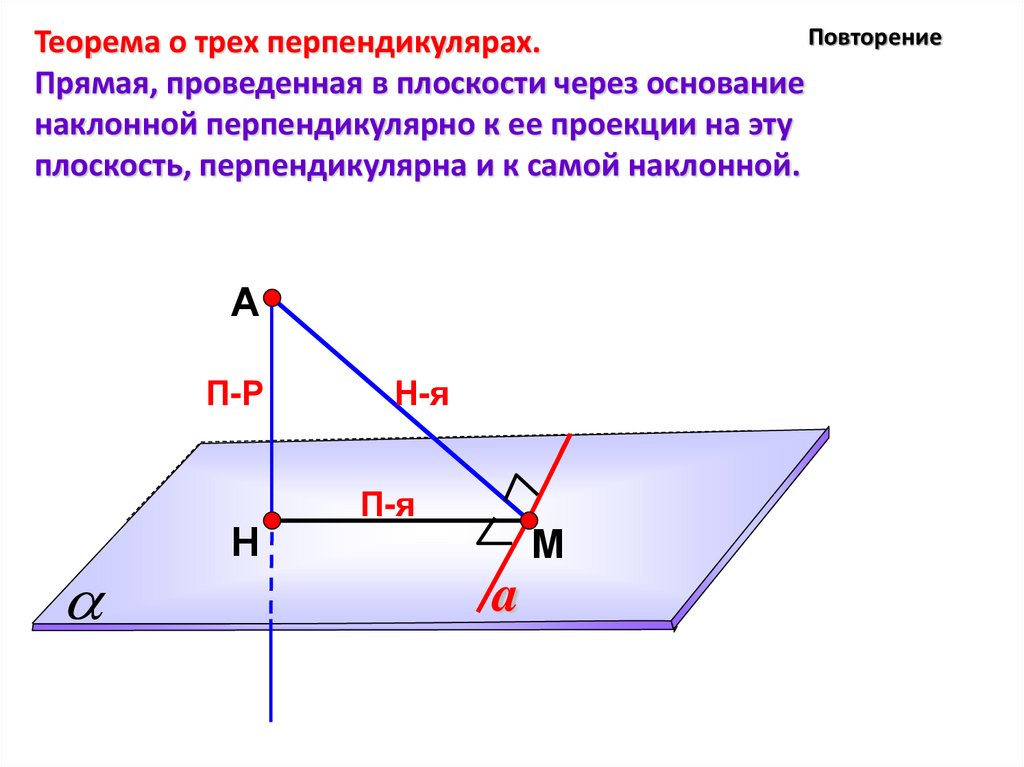
Повторение
Теорема о трех перпендикулярах.
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна и к самой наклонной.
А
П-Р
Н
Н-я
П-я
М
a

4.

Повторение
Определение
Углом между прямой и плоскостью, пересекающей эту прямую и не
перпендикулярной к ней, называется угол между прямой и её
проекцией на плоскость
a
∠АМH — угол между а и α
A
H
M
α

5.

Похоже, к сожалению, не
работает у меня микрофон на
ПК, поэтому весь материал
данной презентации я
прикреплю в электронный
журнал как «Домашнее
задание»!!!

6.

Изучение нового материала
Стр.50 учебника

7.

Линейный угол
B
A
C

8.

9.

Двугранный угол

10.

Двугранный угол
a

11.

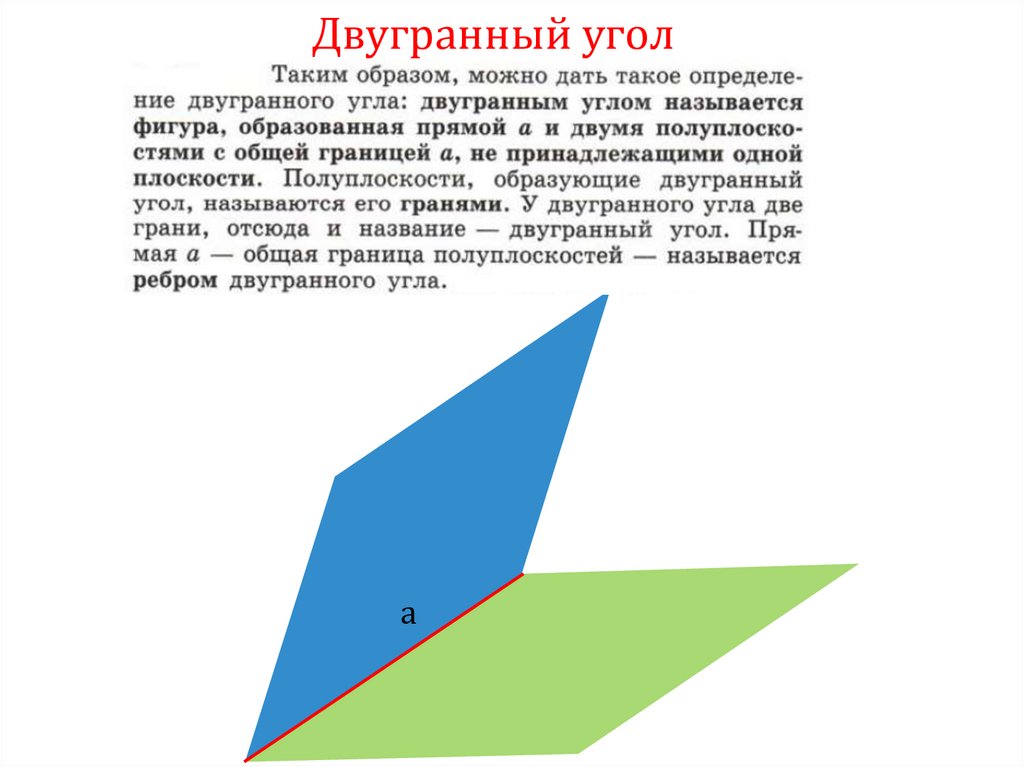
Определение:
Двугранным углом называется
фигура, образованная двумя
полуплоскостями с общей
граничной прямой.
a

12.

Элементы двугранного угла
Полуплоскости,
образующие двугранный угол,
.
называются его гранями.
Общая граница этих полуплоскостей – ребром
двугранного угла.
ребро
а
грани

13.

14.

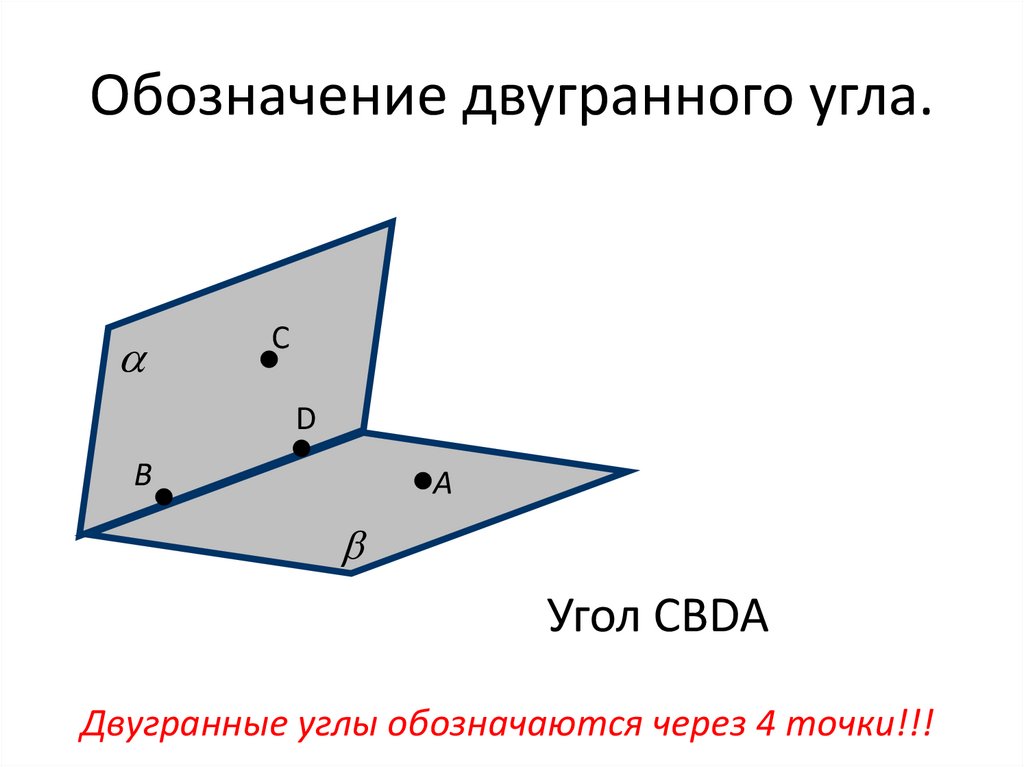
Обозначение двугранного угла.
С
D
В
А
Угол CBDA
Двугранные углы обозначаются через 4 точки!!!

15.

D
двугранных углов 6трёхгранных углов-4
плоских углов -12
A
C
B
Укажите все двугранные углы

16.

17.

Величиной двугранного угла называется
величина его линейного угла.
AF ⊥ CD
BF ⊥ CD
AFB-линейный угол двугранного
угла ACDВ

18.

Линейным углом двугранного угла называется
сечение двугранного угла плоскостью,
перпендикулярной ребру.
С
О
А
D
В

19.

Величина линейного угла не зависит от выбора его
вершины на ребре двугранного угла.
B1
A1
A
O1
O
B
Двугранный угол имеет бесконечное множество линейных углов.

20.

Примеры двугранных углов:

21.

Аналогично тому , как и на плоскости , в пространстве
определяются смежные и вертикальные двугранные
углы.
β
β
а
β1
1
γ
а

22.

Угол между плоскостями
Углом между
двумя
пересекающимися
плоскостями
называется
наименьший из
двугранных углов,
образованных
этими плоскостями.

23.

23. Признак перпендикулярности
двух плоскостей

24.

25.

26.

Признак перпендикулярности двух плоскостей

27.

28.

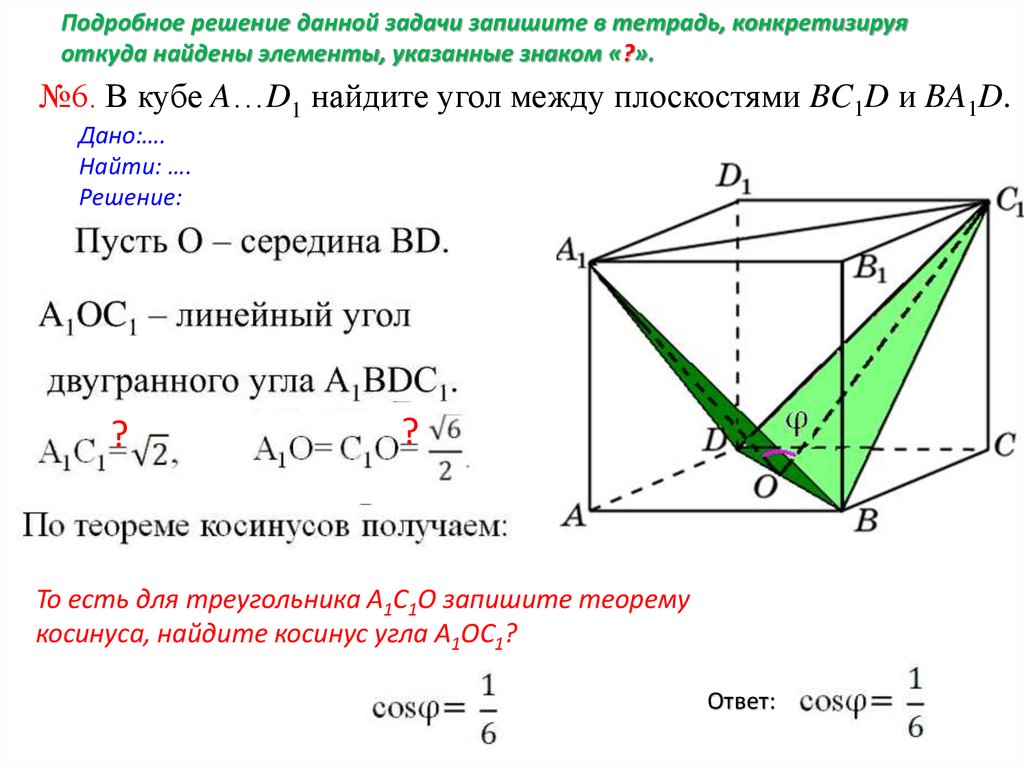
№1
В кубе A…D1
найдите угол
между
плоскостями
ABC и CDD1.
Ответ: 900

29.

№2
В кубе A…D1
найдите угол
между
плоскостями
ABC и CDA1.
Ответ: 450

30.

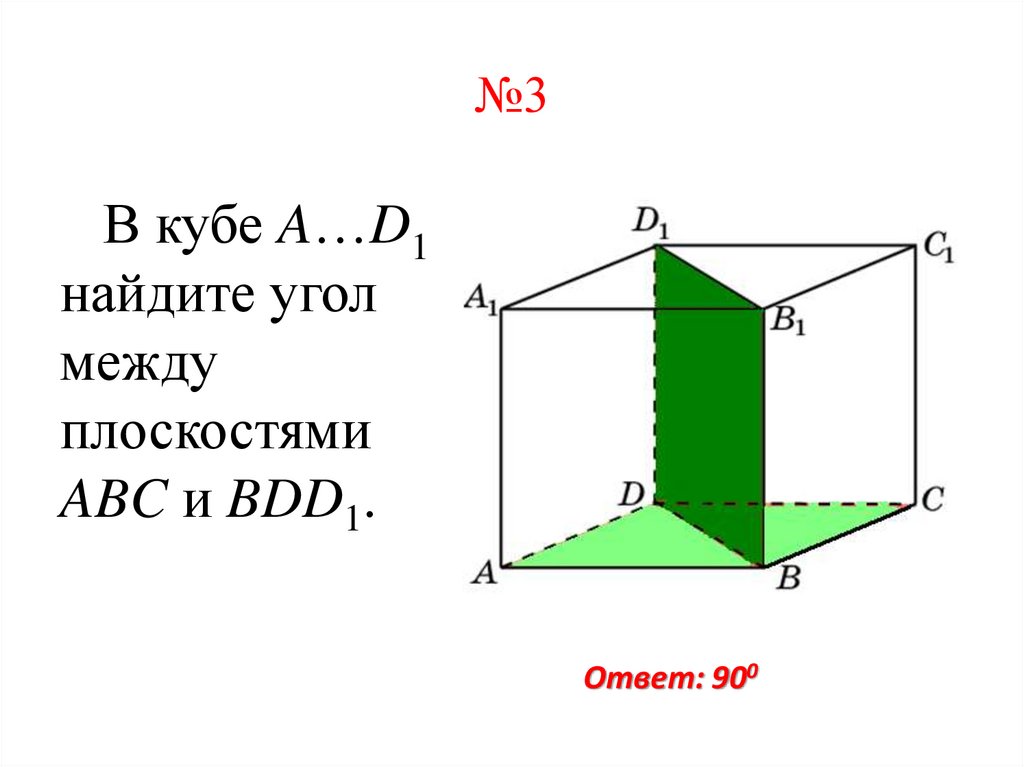
№3
В кубе A…D1
найдите угол
между
плоскостями
ABC и BDD1.
Ответ: 900

31.

№4
В кубе A…D1
найдите угол
между
плоскостями
ACC1 и BDD1.
Ответ: 900

32.

№5
В тетраэдре DABC все ребра равны, точка М – середина
ребра АС. Докажите, что ∠DMB – линейный угол
двугранного угла BACD.
Треугольники ABC и ADC
правильные, поэтому, BM⊥AC
и DM⊥AC и, следовательно,
∠DMB является линейным
углом двугранного угла DACB.

33.

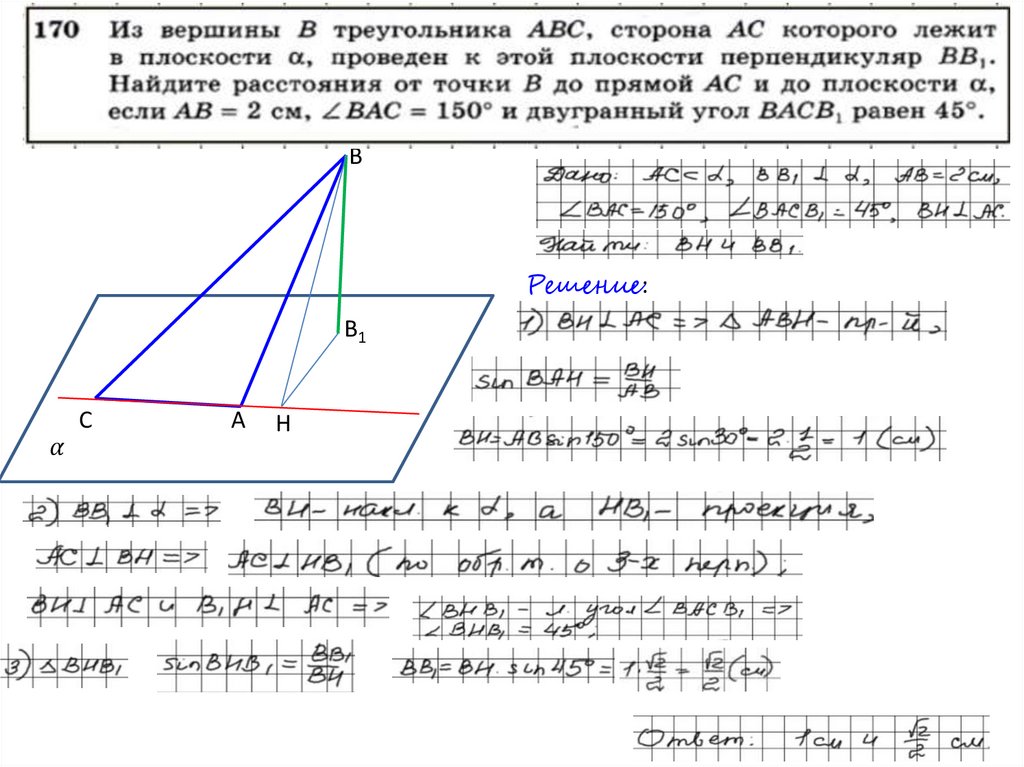
В
Решение:
В1