Similar presentations:
Дифференциальные уравнения. Основные определения и некоторые физические задачи, приводящие к дифференциальным уравнениям
1.
Дифференциальные уравнения§ 1. Основные определения и некоторые физические задачи,
приводящие к дифференциальным уравнениям
Дифференциальными уравнениями (ДУ) называют уравнения, в
которые неизвестная функция входит под знаком производной или
дифференциала.
Решением дифференциального уравнения называют функцию,
которая при подстановке в уравнение обращает его в тождество.
Процесс нахождения решений называют интегрированием
дифференциального уравнения, а график решения – интегральной
кривой.
Обыкновенными дифференциальными уравнениями (ОДУ)
называют дифференциальные уравнения, если неизвестная функция
зависит от одной переменной. Если неизвестная функция зависит от
двух и более переменных, то ДУ называют дифференциальным
уравнением в частных производных.
2.
Порядком дифференциального уравнения называют наивысшийпорядок производной, входящей в уравнение.
dx
Пример.
kx . Это ДУ первого порядка – уравнение
dt
радиоактивного распада; k – постоянная распада, х – количество
неразложившегося вещества в момент времени t, dx dt – скорость
распада.
dT
k T Tc . Это ДУ первого порядка – уравнение
Пример.
dt
охлаждения нагретого тела, T – температура тела, Tс – температура
окружающей среды, t – время, k – коэффициент, зависящей от
свойств тела, среды и т.д.
d 2r
Пример. m 2 F . Это ДУ второго порядка – уравнение
dt
движения точки массы т под действием силы F; t – время, r –
радиус-вектор точки.
3.
§ 2. Дифференциальные уравнения первого порядка.Изоклины. Задача Коши.
Обыкновенное дифференциальное уравнение первого порядка
в общем случае имеет вид
F x, y , y 0 .
Обыкновенное дифференциальное уравнение первого порядка,
разрешенное относительно производной, имеет вид
(2.1)
y f ( x, y ) .
Пусть l – интегральная кривая Y
уравнения (2.1). Тогда y f ( x, y ) – это
B
M(x,y)
угловой коэффициент касательной AB к y
l
A
кривой l в точке M x, y (рис. 2.1).
Следовательно,
дифференциальное
уравнение (2.1) определяет в каждой точке
x
X
плоскости OXY направление касательной к O
Рисунок 2.1
интегральной кривой, проходящей через эту
точку, т.е. определяет поле направлений. В этом заключается
геометрический смысл дифференциального уравнения
первого
порядка.
4.
dy yПример.
. В каждой точке плоскости, кроме начала
dx x
y
координат, угловой коэффициент к интегральной кривой равен
–
x
тангенсу угла, образованного с осью OX
Y
прямой, проходящей через данную точку и
начало координат (рис. 2.2). Интегральными
кривыми в данном случае будут прямые вида
O
X
y Cx .
Рисунок 2.2
Изоклинами называют геометрическое место точек плоскости, в
которых касательные к интегральным кривым сохраняют
постоянное направление; в этих точках выполняется соотношение
dy
const .
dx
5.
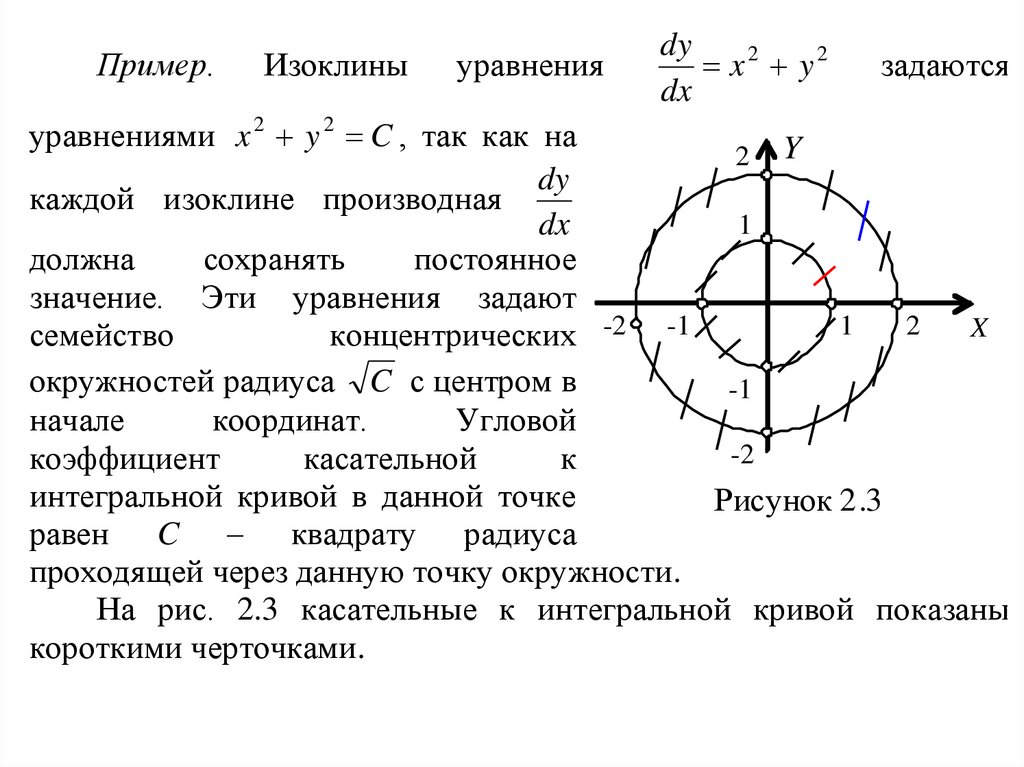
Пример.Изоклины
уравнения
dy
x2 y2
dx
задаются
уравнениями x 2 y 2 C , так как на
2 Y
dy
каждой изоклине производная
1
dx
должна
сохранять
постоянное
значение. Эти уравнения задают
1
2
X
семейство
концентрических -2 -1
окружностей радиуса C с центром в
-1
начале
координат.
Угловой
-2
коэффициент
касательной
к
интегральной кривой в данной точке
Рисунок 2.3
равен C – квадрату радиуса
проходящей через данную точку окружности.
На рис. 2.3 касательные к интегральной кривой показаны
короткими черточками.
6.
Условие, что при x x 0 функция y должна быть равназаданному числу y0, называют начальным условием и записывают в
виде
(2.2)
y x0 y0 или y x x y 0
0
Общим решением дифференциального уравнения первого
порядка называют функцию y x, C , содержащую произвольную
постоянную C и удовлетворяющую условиям:
1) функция y x, C является решением ДУ при любом
фиксированном значении C.
2) при любом начальном условии (2.2) можно найти такое
значение постоянной
C C 0 , что функция
y x;C 0
удовлетворяет данному начальному условию.
Если общее решение дифференциального уравнения найдено в
неявном виде x; y; C 0 , то такое решение называют общим
интегралом.
7.
Частным решением дифференциального уравнения первогопорядка называют функцию y x;C 0 , полученную из общего
решения y x, C при конкретном значении постоянной C C 0 .
Если частное решение дифференциального уравнения найдено
в неявном виде x; y; C0 0 , то его называют частным
интегралом.
Задачей Коши называют задачу нахождения решения
уравнения y f ( x, y ) , удовлетворяющего начальному условию
y x0 y0 . Если рассматривать множество всех решений ДУ (2.1)
как множество интегральных кривых на плоскости, то задача Коши
– это нахождение такой кривой, которая проходит через точку
x0 , y 0 .
Теорема существования и единственности решения задачи
Коши. Если в некоторой окрестности точки x0 , y0 функция f ( x, y )
в уравнении y f ( x, y ) определена, непрерывна и имеет
непрерывную частную производную f y , то существует окрестность
точки x0 , y0 , в которой задача Коши имеет решение и притом
единственное.
8.
Особыми называют точки, в которых не выполняются условиятеоремы Коши.
§ 3 Дифференциальные уравнения первого порядка
Дифференциальные
уравнения
первого
порядка
с
разделяющимися переменными имеет вид
(3.1)
f y dy g x dx
Любое решение y x этого уравнения будет удовлетворять
уравнению
f ( y)dy C1 g ( x)dx C2
или
f ( y)dy g ( x)dx C ,
где C C 2 C1 – произвольная постоянная.
Пример. Решить уравнение y 2 1dx xydy .
Разделяя переменные и интегрируя, получим
(3.2)
9.
ydydx
dx
или
C.
2
2
x
y 1 x
y 1
dx
Интеграл в правой части - табличный - ln x .
x
Чтобы взять интеграл в левой части уравнения, введем новую
ydy
переменную u y 2 1 . Тогда получим
du
2y
y
или du
2
2
dy 2 y 1
y 1
Тогда
ydy
y2 1
du u y 2 1 .
Окончательно получим решение ДУ
y 2 1 ln x C
ydy
y2 1








 mathematics
mathematics








