Similar presentations:
Фазовые переходы в газонасыщенной жидкости
1.
Фазовые переходы вгазонасыщенной жидкости
2.
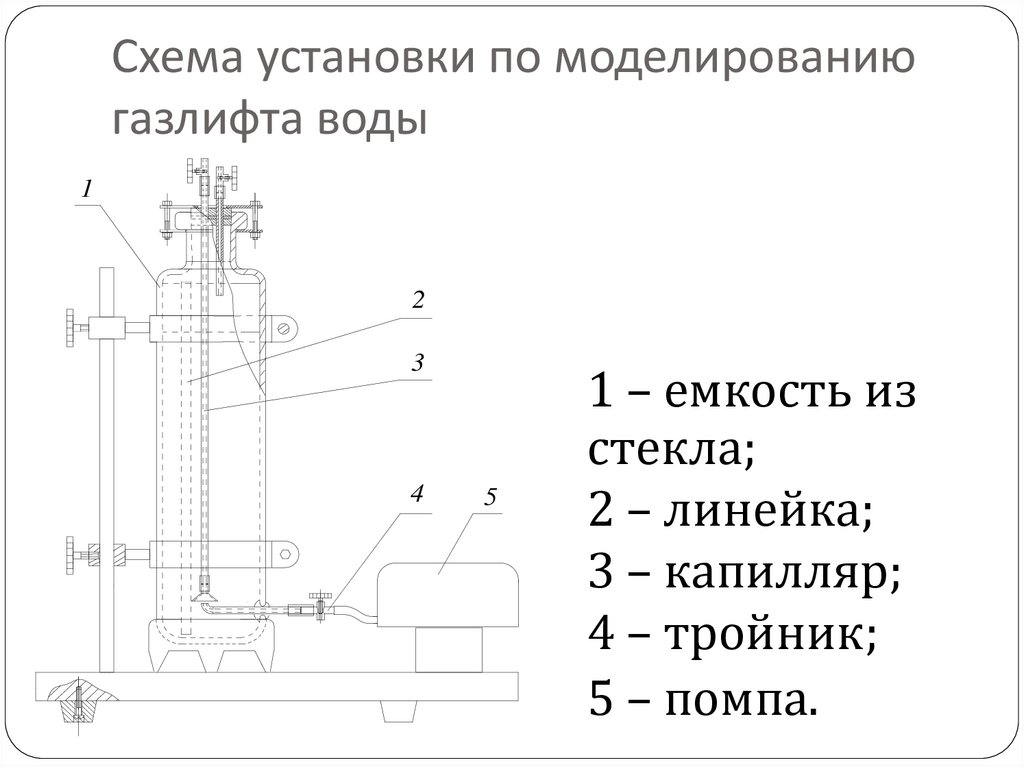
Схема установки по моделированиюгазлифта воды
1
2
3
4
5
1 – емкость из
стекла;
2 – линейка;
3 – капилляр;
4 – тройник;
5 – помпа.
3.
Основное уравнение динамикигазовых пузырьков в жидкости
Функция распределения
f r t , v t ,V t , N t , t
r t
Координата пузырька
v t
Скорость пузырька
V t
Объем пузырька
N t
Плотность атомов газа пузырька
4.
Пространственные переменныеи время
r (t ), v(t ),V (t ), N (t )
t
Вводим безразмерное число N1 (t ) V (t ) V0
изменение объема пузырька
за время
t
За это время
с модулем
V0
r (t ) меняется на r0
3 3
4
V0 со скоростью
r0
v(t )
t
5.
Для функции распределения газовых пузырьковсправедливо преобразование подобия
f (r (t ), v(t ), V (t ), N (t ), t )dV f (r (t ), v(t ), N1 (t ), N (t ), t ) dN1
или
V0 f (r (t ), v(t ), V (t ), N (t ), t ) f (r (t ), v(t ), N1 (t ), N (t ), t )
С учетом этого, изменение во времени функции
распределения
f (r (t ), v(t ), N1 (t ), N (t ), t ) f (Qi , N1 (t ), N (t ), t )
где: Qi набор векторов , который обозначает координату
(i=1) и скорость (i=2 ) центра пузырька
6.
Представим в видеI N I N1
df
I N I N 1 I N I N 1
1
1
dt
N N1
где: I N - поток в пространстве
N
I N1 - поток в пространстве N1
I N N , N 1 f (Qi , N1 , N , t ) N 1, N f (Qi , N1 , N 1, t )
IN
1
N1 , N1 1
f (Qi , N1 , N , t ) N 1, N f (Qi , N1 1, N , t )
1
1
7.
ГдеK , K 1 - частота перехода из состояния K
в состояние K+1, где Ê N , N,1 K 1, K - частота
обратного перехода из состояния K+1 в состояние K.
Далее считаем, что
f (Qi , N1 1, N , t ) f
Уравнение изменения во времени функции
распределения можно преобразуется к уравнению
диффузии в пространстве [N,V ]
8.
ff
f
( N , V ) f
D( N )
D(V )
t
N
N V
V
где
dN dN
dV dV
( N , V )
sign
sign
N
dt dt V
dt dt
dN dV
d dN dV sign dt dt
ln
dt dt dt
9.
df (Qi , N1 1, N , t )dN
IN
f (Qi , N1 1, N , t ) D( N )
dt
dN
df (Qi , N1 1, N , t )
dV
IV
f (Qi , N1 1, N , t ) D(V )
dt
dV
dN
1 F (V , N )
D( N )
,
dt
T
N
D L
2
D( N ) N , N 1 4 R
n
2l
10.
F (V , N )p
T ln V
N
p
dV
1 F (V , N )
D(V )
,
dt
T
V
3VT
2
D(V ) N , N 1 V0
1 1
4
2 R
F (V , N )
L
V
p p
V
R
11.
F (V , N ) V p p NL
V
V
L
V 2 R'
0
R'
dV '
F (V , N ) - разность свободной энергий среды с
4 3 и числом атомов N
пузырьком объема V
R
3
и свободной энергий среды с растворенным газом без
пузырька; T - температура среды; nL - плотность газа в
жидкости; V- химический потенциал атома газа в
пузырьке; - химический потенциал атомов газа в
жидкости;
L
12.
V-pдавление
газа
p насыщающее давление газа;
V
в пузырьке; p - давление в вязкой жидкости;
R - коэффициент поверхностного натяжения на
- динамическая
0 1
- коэффициент,
границе жидкость-вакуум;
вязкость жидкости;
учитывающий дополнительный барьер, для последнего
скачка атома газа в пузырек; D - коэффициент диффузии
атомов газа в среде; l - длина элементарного
перемещения атома газа в среде.
13.
Уравнение должно быть дополнено уравнением,описывающим сохранение числа атомов газа в единичном
объеме, включающем атомы газа в пузырьках и атомы газа,
растворенные в жидкости:
n 0 1 Vf (V , N , t )dVdN
00
L
n t 1 Vf (V , N , t )dVdN Nf (V , N , t )dVdN
00
00
L
Или в таком виде:
L
1 n t f V , N , t dVdN Nf V , N , t dVdN
0 0
0 0
1 n L 0
14.
При переходе к этому выражению использованапропорциональность количества газовых пузырьков и
изменение объема жидкости в единичном объеме:
1 f V , N , t dVdN 1 Vf V , N , t dVdN
0 0
00
Для решения уравнения динамики пузырьков газа в
среде систему уравнений необходимо дополнить
начальными и граничными условиями.
Однако, в некоторых случаях, удается получить
автомодельные решения уравнения, которые
характеризуют его внутренние свойства
безотносительно от вида начальных и граничных
условий
15.
Условия существования и параметрыстационарных пузырьков в жидкости при
dN dV
0
dt dt
Условие, при котором реализуется стационарное
распределение газовых пузырьков
i
L
p, p , n const ,
или
i V,L
( N , V ) 0
Количество газовых пузырьков N b f
V , N dNdV
постоянно, но параметры их могут изменяться во времени.
16.
dN dV0
Рассмотрим случай, когда
dt dt
Из условия стационарности процесса следует
V t C1,2 N t D1,2
C1,2 , D1,2 - константы интегрирования,
C1 W0 n 0
L
1
- элементарный объем.
Из условия ( N , V ) 0 , представления Толмена для
R
коэффициента поверхностного натяжения R
,
R
где - поверхностное натяжение жидкости при R
17.
Предполагая выполнение условия равновесия давленияна поверхности пузырька p
L
R
,
t
p
получим
выражение для стационарного радиуса пузырька Rb
Rb2 l
2
2 W0 Dn ln 1 L
2
p Rb
Rb
L
18.
В водопроводной воде 30 Rb 2 R0, где R3A
– эффективный радиус “атома” воздуха. При
0
и 1 получим 1, 6 10
6
Rb
см.
6 см, и в дальнейшем
6,
6
10
b
С учетом этого R
параметр учитывать не будем.
19.
Условия существования и параметры стационарных пузырьков в жидdN dVкости при
0
dt
dt
3V V
2
dV
dV
L
M0
M 0 p p R R
dN
dt
T
4
2
M0
- константа
2
20.
N.
Рис. 1. Зависимости объема равновесного газового
пузырька V N
от количества атомов газа в
нем N
21.
Динамика газовых пузырьков вжидкости при уменьшении внешнего
давления
dN dV
0
dt dt
Поиск автомодельных решений при
Пусть p (t )
p(t ) p0 t t0 t
0
p p t t0 t , p p t t0 t0
L
L
0
0
V
Введем автомодельную функцию ,
и автомодельные переменные
и
V
0
22.
, f V , N , t t t0 t3V
3
3
t
t
t
0 0
4
0
N t t0 t0
, - показатели степени, определяемые из
f
f
f
( N , V ) f
D( N )
D(V )
t
N
N V
V
Условие стационарности:
и
, ,
0
n t const приводят исходное уравнение к виду
L
23.
Vt0
p
D L
0
n ln L
1 2 W0
2 R0
l
p0
Где
R0 - начальный радиус пузырька и справедливо
соотношениеp
R, t p
L
. Из полученного уравнения
следует:
R0 Rb 0
R0 Rb 0
R0 Rb 0
24.
Динамика газовых пузырьков в водепри уменьшении внешнего давления
Среднее число пузырьков
в жидкости
Средний размер
пузырьков в жидкости
N b t f (V , N , t )dVdN
0 0
V t Vf (V , N , t )dVdN
0 0
Среднее количество
атомов газа в пузырьке
N t W V t
1
0
25.
Из закона сохранения атомов газа в единичном объемежидкости N b N 1 n L
следует, что
t const
и nL
t const
7,5
№ диапазона
1
2
3
4
5
6 6 6 9 9 9
Nb t
+
0
—
—
—
V t , N t
+
+
+
0
—
26.
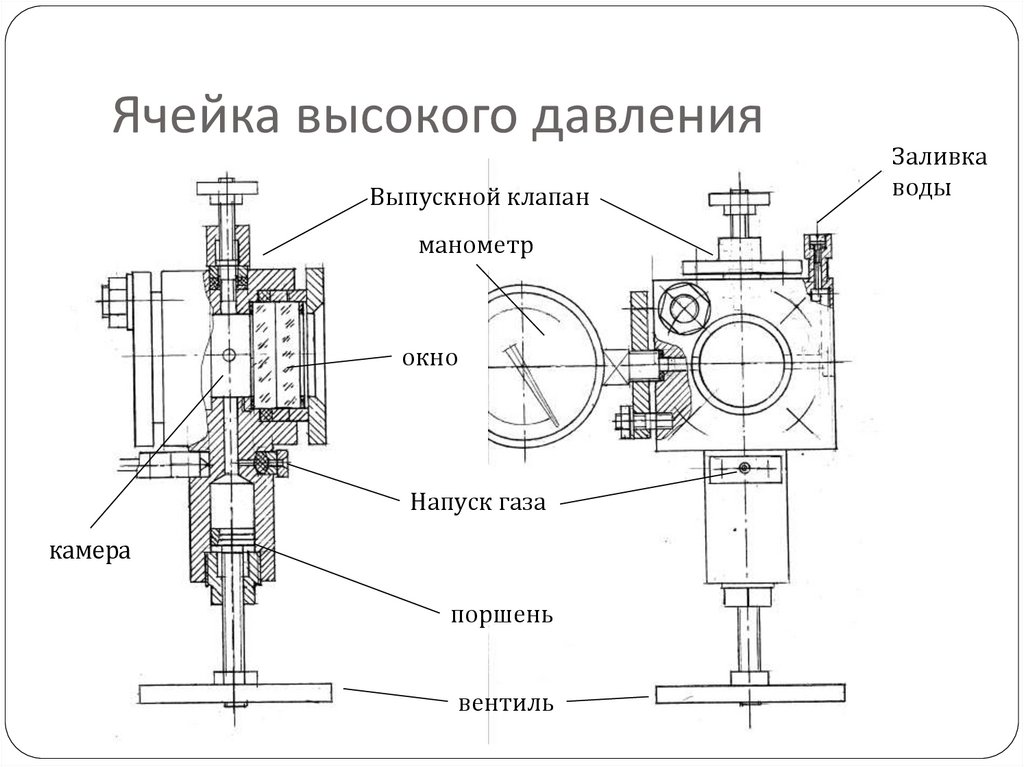
Ячейка высокого давленияВыпускной клапан
манометр
окно
Напуск газа
камера
поршень
вентиль
Заливка
воды
27.
Состояния «до» и «после»28.
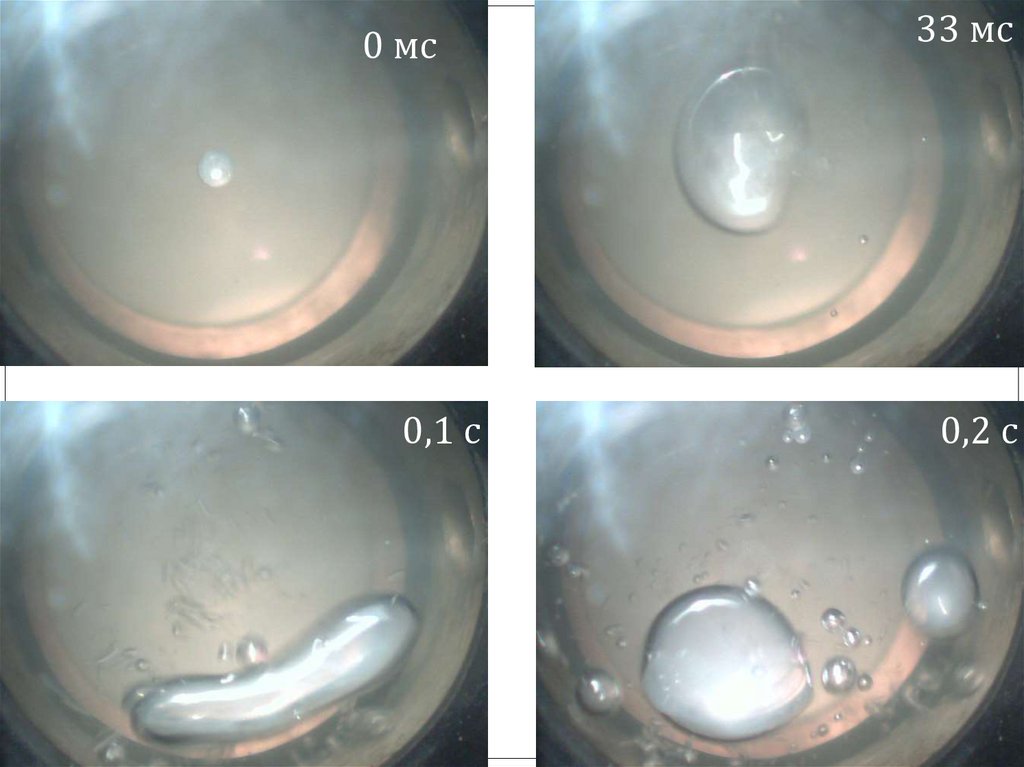
Динамика образования пузырьков29.
0 мс0,1 с
33 мс
0,2 с
30.
0,3 с0,5 с
1с
2,67 с







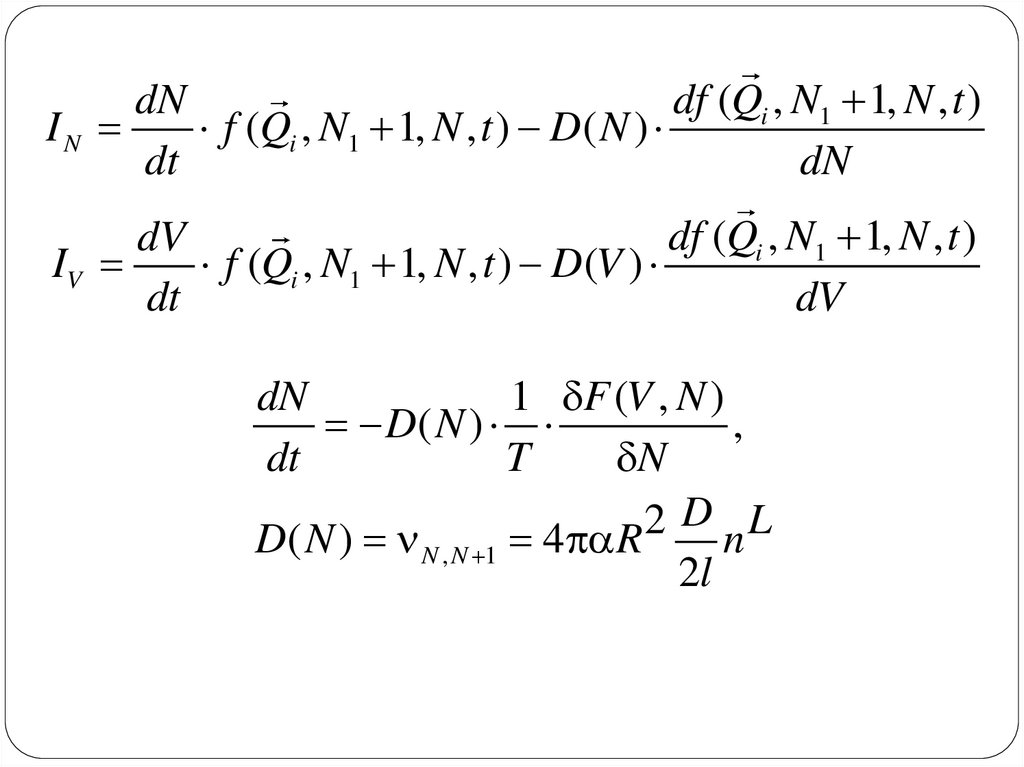



















 physics
physics








