Решение неравенств второй степени с одной переменной

1. Решение неравенств второй степени с одной переменной

2. Цель:

Сформировать умения решать неравенства
ах² + вх +с >0 (ах² + вх +с ≥0 ),
ах² + вх +с < 0 (ах² + вх +с ≤ 0),
где а ≠ 0, с опорой на сведения о графике
квадратичной функции (направление ветвей
параболы, ее расположение относительно оси 0х).

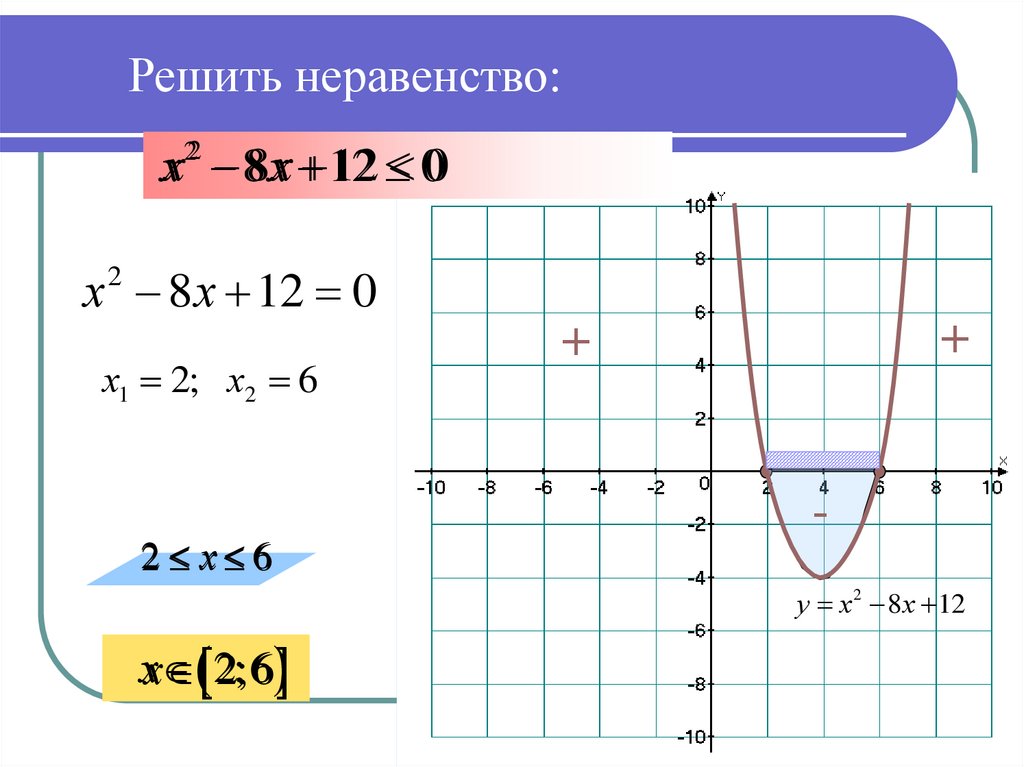
3. Решить неравенство:

х22 8 х 12 0
х 8 х 12 0
2
х1 2; х2 6
2
х
6
+
+
у х 2 8 х 12
х
х 2;6

4. Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0 поступают следующим образом:

Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0
поступают следующим образом:
Находят дискриминант квадратного трехчлена и выясняют, имеет
ли трехчлен корни;
Если трехчлен имеет корни, то отмечают их на оси х и через
отмеченные точки проводят схематически параболу, ветви которой
направлены вверх при а >0 или вниз при а < 0; если трехчлен
не имеет корней, то схематически изображают параболу,
расположенную в верхней полуплоскости при а >0 и в нижней при
а < 0;
Находят на оси х промежутки, для которых точки параболы
расположены выше оси х ( если решают неравенство ах² + вх +с >0
или ниже оси х (если решают неравенство ах² + вх +с < 0).

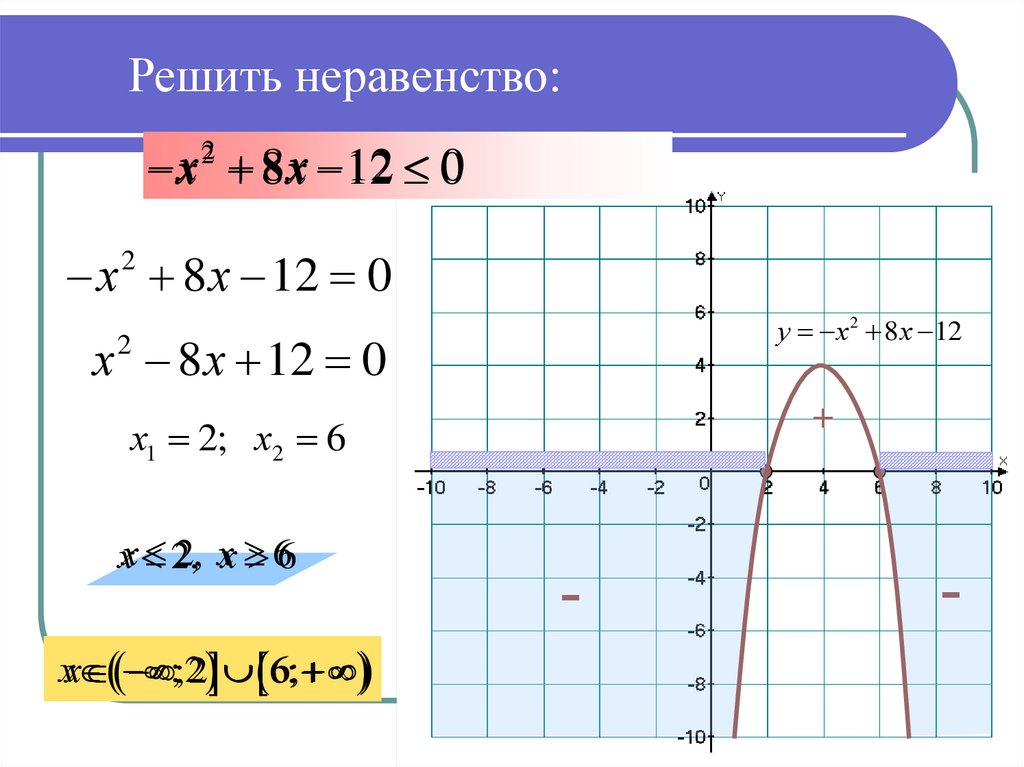
5. Решить неравенство:

х 8 х 12 0
2
х 8 х 12 0
х 8 х 12 0
2
2
х1 2; х2 6
2, хх 66
х
+
+
у х 2 8 х 12
х ;2 6;
6;

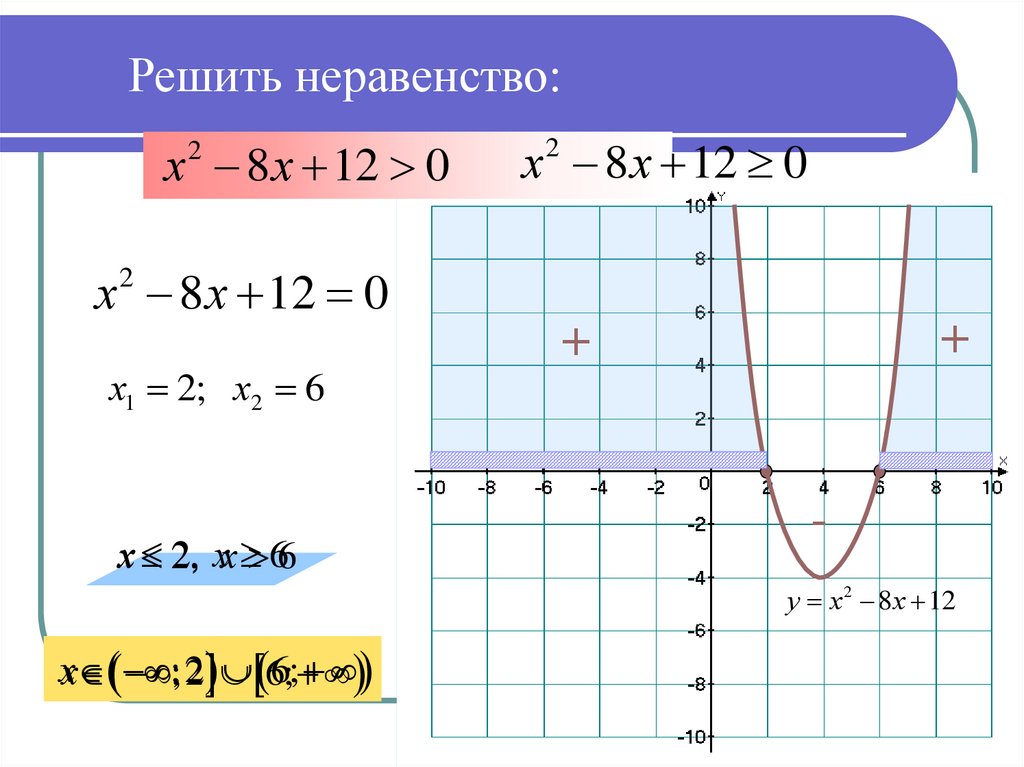
6. Решить неравенство:

х 2 8 х 12
0
х 8 х 12 0
2
х 8 х 12 0
2
х1 2; х2 6
2
х
6
х
х 2;6
у х 2 8 х 12
+

7. Решить неравенство:

х 2 8 х 12
0
х 8 х 12 0
2
у х 2 8 х 12
х 8 х 12 0
2
+
х1 2; х2 6
2, х 66
хх 2,
х
х
;2
;2 6;
-
-

8. Решить неравенство:

х 4 х 4 0
22
у х2 4х 4
х 4х 4 0
2
D 0;
х 2
Нетхрешений
2
+
+

9. Решить неравенство:

х2 4 х 4
0
у х2 4х 4
х 4х 4 0
2
D 0;
х 2
х х2, хR 2
х ;2
х
; 2;
+
+

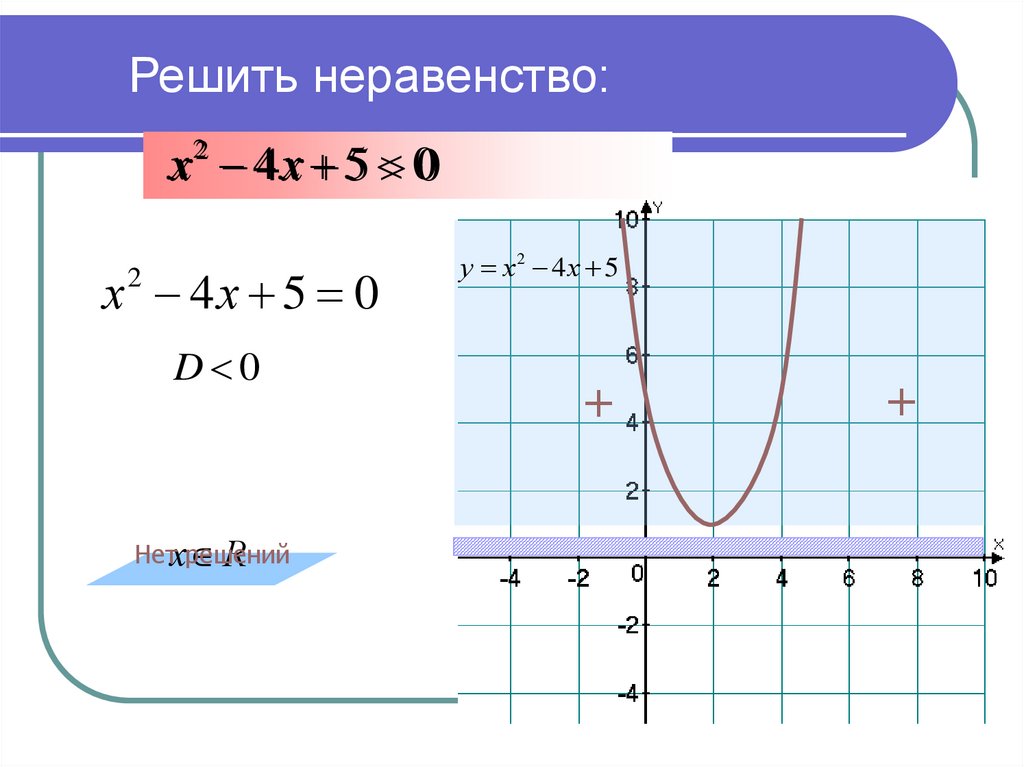
10. Решить неравенство:

х 4 х 5 0
22
х 4х 5 0
2
D 0
Нетхрешений
R
у х2 4 х 5
+
+

11. Решить неравенство:

х 44хх 55 00
2
х 4х 5 0
2
D 0
Нетхрешений
R
-
у х2 4х 5

12. Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0 поступают следующим образом:

Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0
поступают следующим образом:
Находят дискриминант квадратного трехчлена и выясняют, имеет
ли трехчлен корни;
Если трехчлен имеет корни, то отмечают их на оси х и через
отмеченные точки проводят схематически параболу, ветви которой
направлены вверх при а >0 или вниз при а < 0; если трехчлен
не имеет корней, то схематически изображают параболу,
расположенную в верхней полуплоскости при а >0 и в нижней при
а < 0;
Находят на оси х промежутки, для которых точки параболы
расположены выше оси х ( если решают неравенство ах² + вх +с >0
или ниже оси х (если решают неравенство ах² + вх +с < 0).

13. Домашнее задание

п.14 читать, рассмотреть примеры, выписать
алгоритм
№ 304, 305, 306 ( везде а, в)