Similar presentations:
Неравенства. Способы решения
1.
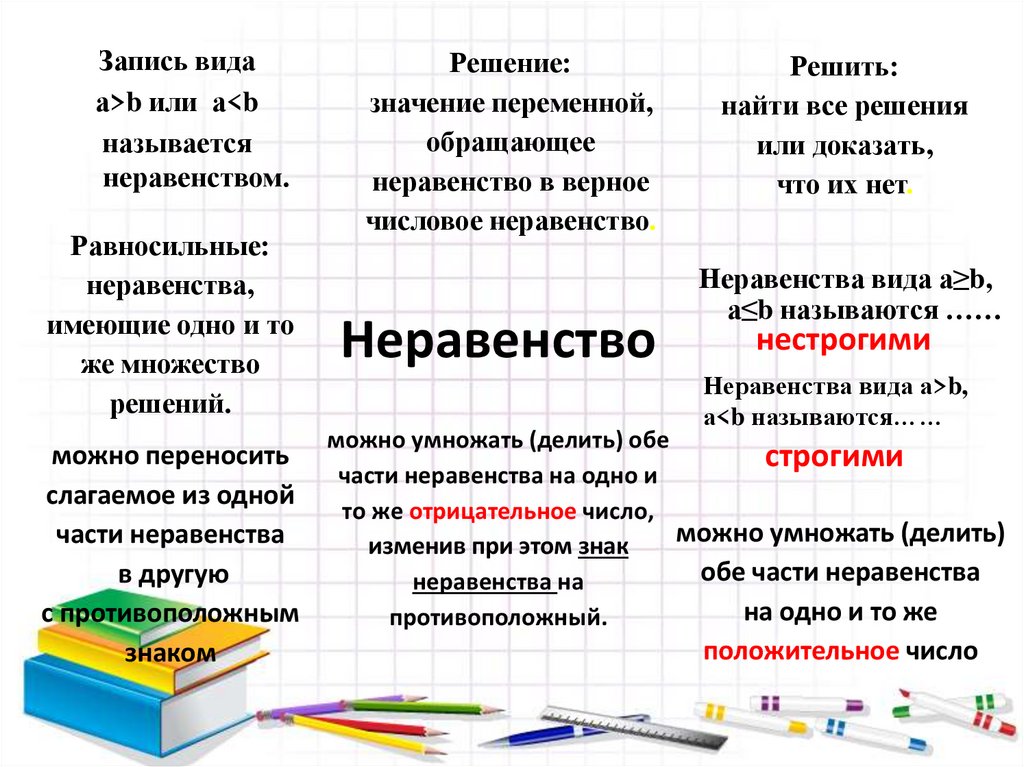
Запись видаа>b или а<b
называется
неравенством.
Равносильные:
неравенства,
имеющие одно и то
же множество
решений.
можно переносить
слагаемое из одной
части неравенства
в другую
с противоположным
знаком
Решение:
значение переменной,
обращающее
неравенство в верное
числовое неравенство.
Неравенство
Решить:
найти все решения
или доказать,
что их нет.
Неравенства вида а≥b,
а≤b называются ……
нестрогими
Неравенства вида а>b,
а<b называются……
можно умножать (делить) обе
строгими
части неравенства на одно и
то же отрицательное число,
можно умножать (делить)
изменив при этом знак
обе части неравенства
неравенства на
на одно и то же
противоположный.
положительное число
2.
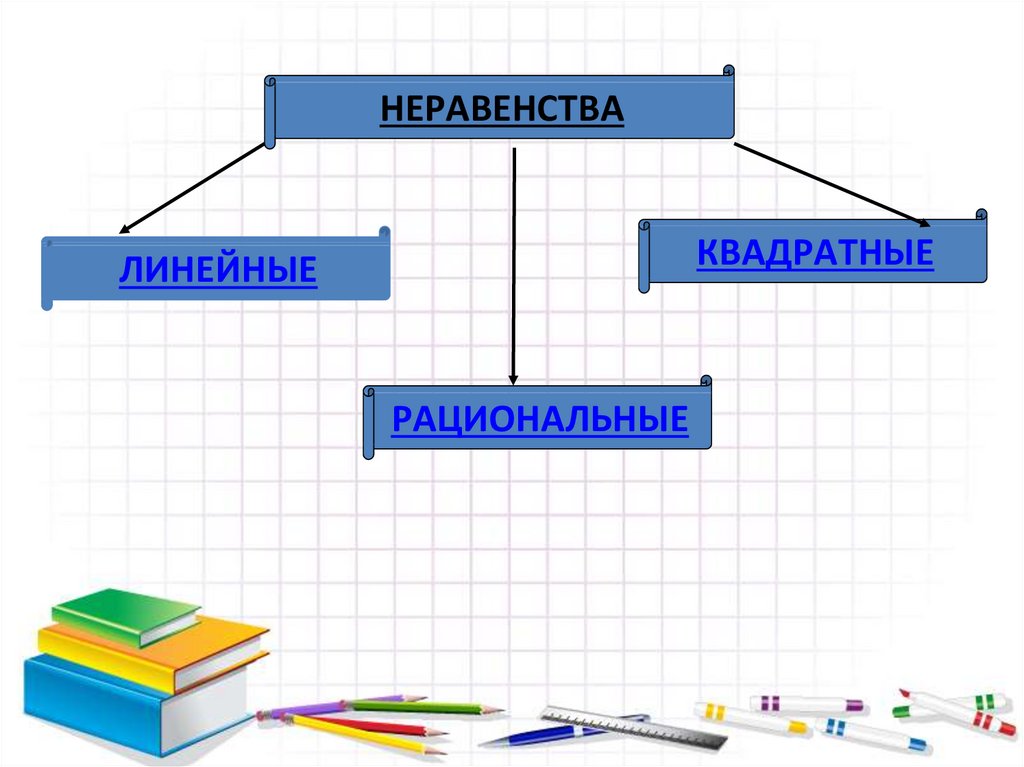
НЕРАВЕНСТВАКВАДРАТНЫЕ
ЛИНЕЙНЫЕ
РАЦИОНАЛЬНЫЕ
3.
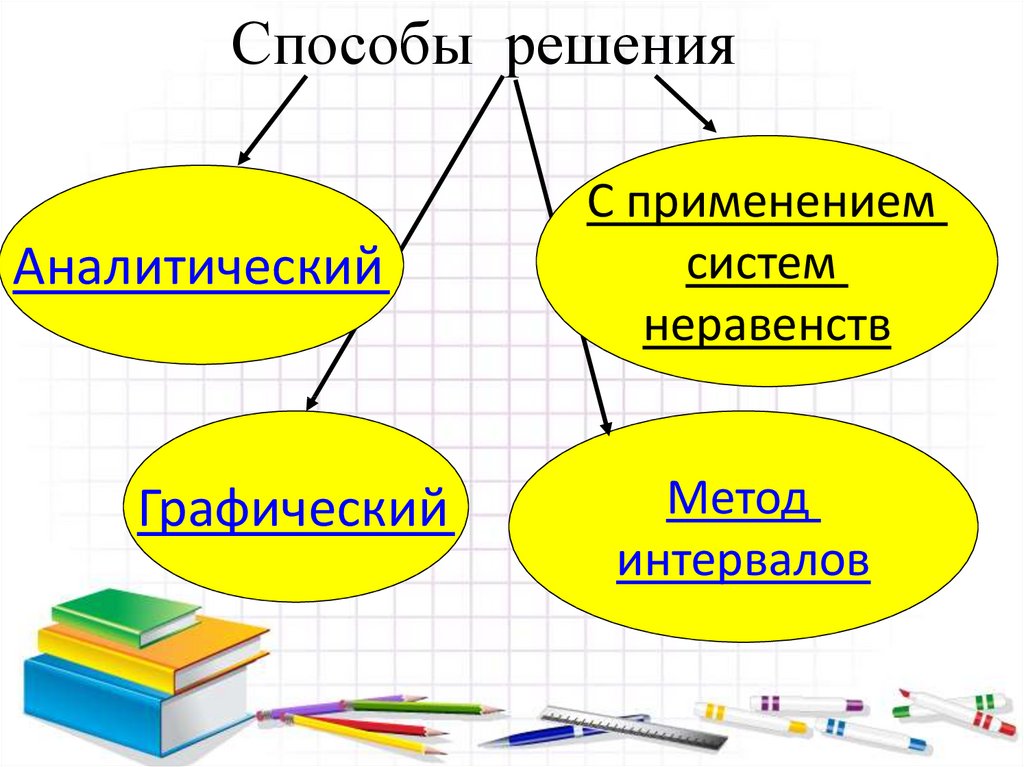
Способы решенияАналитический
Графический
С применением
систем
неравенств
Метод
интервалов
4.
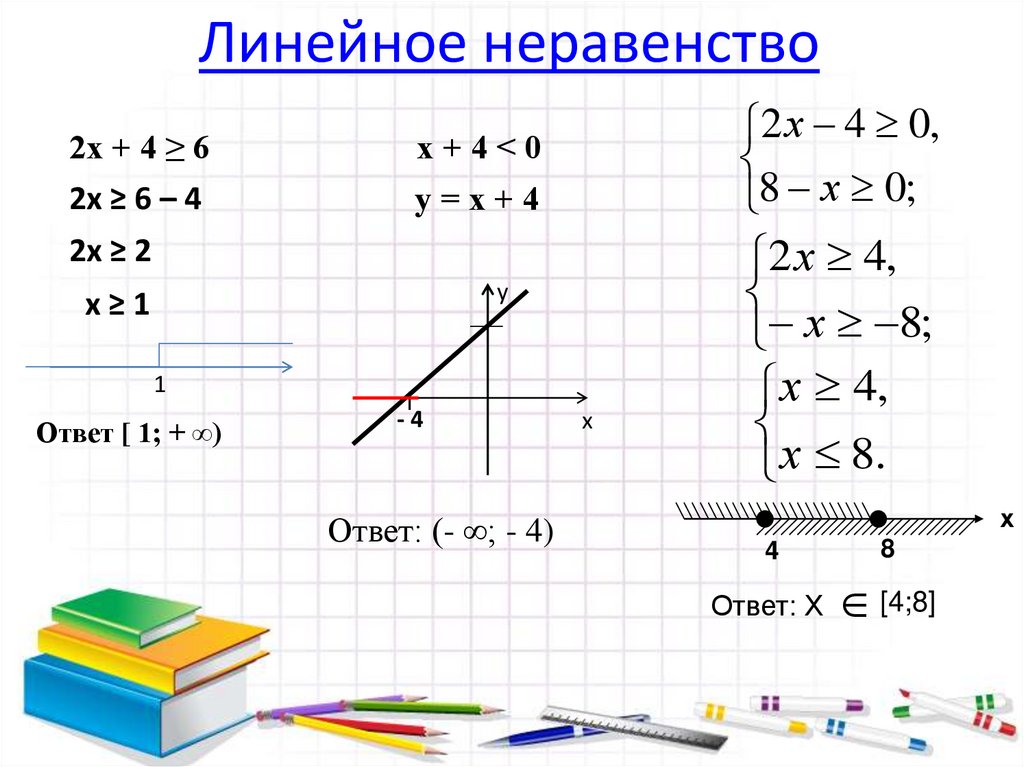
Линейное неравенство2х + 4 ≥ 6
2х ≥ 6 – 4
2 х 4 0,
8 х 0;
х+4˂0
у=х+4
2х ≥ 2
у
х≥1
1
Ответ [ 1; + ∞)
-4
Ответ: (- ∞; - 4)
х
2 х 4,
х 8;
х 4,
х 8.
х
4
8
Ответ: Х
[4;8]
5.
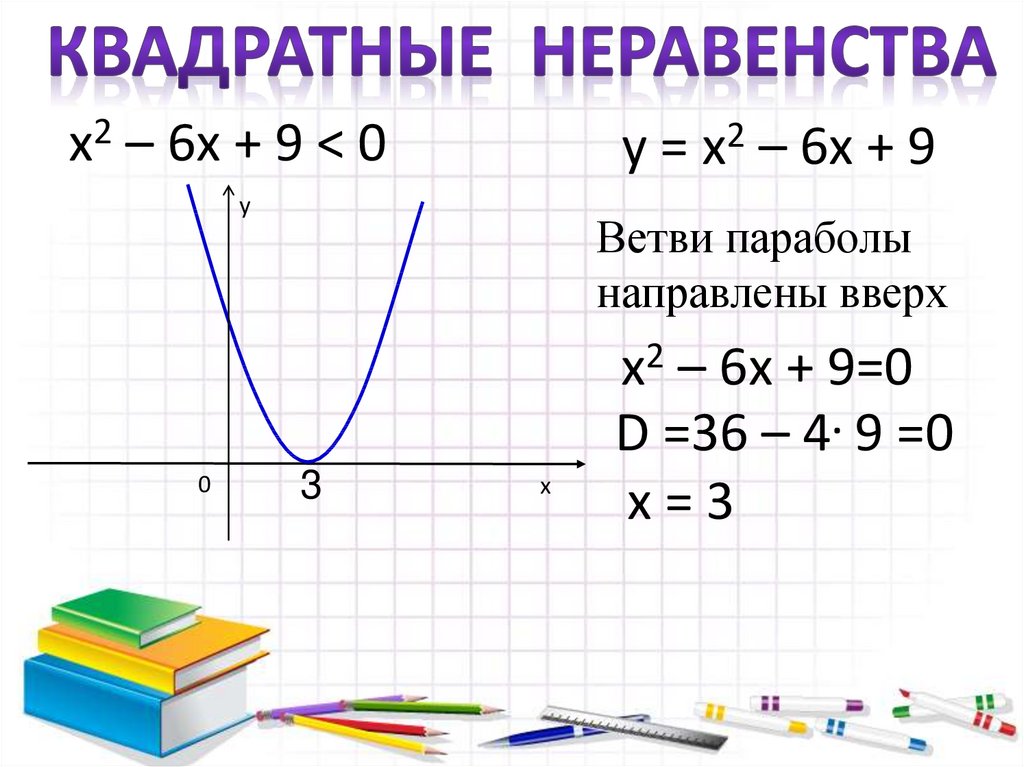
х2 – 6х + 9 < 0у = х2 – 6х + 9
у
0
Ветви параболы
направлены вверх
3
х
х2 – 6х + 9=0
D =36 – 4. 9 =0
х=3
6.
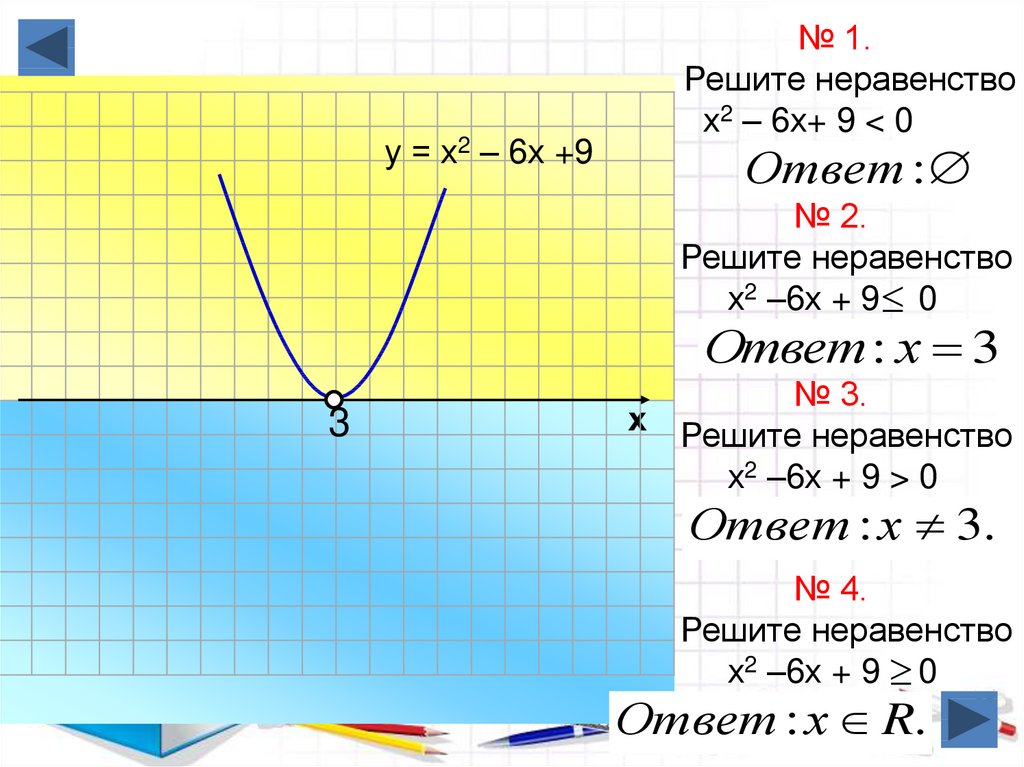
у = х2 – 6х +9№ 1.
Решите неравенство
х2 – 6х+ 9 < 0
Ответ :
№ 2.
Решите неравенство
х2 –6х + 9 0
Ответ : х 3
3
№ 3.
х Решите неравенство
х2 –6х + 9 > 0
Ответ : х 3.
№ 4.
Решите неравенство
х2 –6х + 9 0
Ответ : х R.
7.
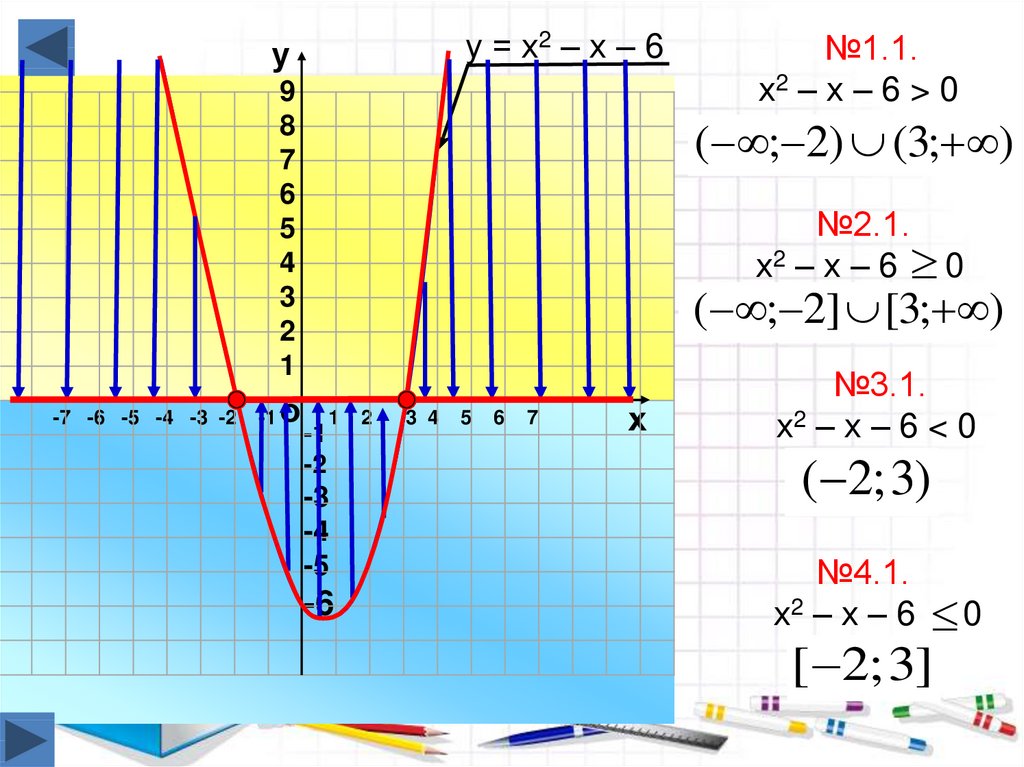
у = х2 – х – 6у
9
8
7
6
5
4
3
2
1
-7 -6 -5 -4 -3 -2
-1
о
№1.1.
х2 – х – 6 > 0
( ; 2) (3; )
№2.1.
х2 – х – 6 0
( ; 2] [3; )
-1
-2
1
-3
-4
-5
-6
2
3 4
5
6
7
х
№3.1.
х2 – х – 6 < 0
( 2; 3)
№4.1.
х2 – х – 6
0
[ 2; 3]
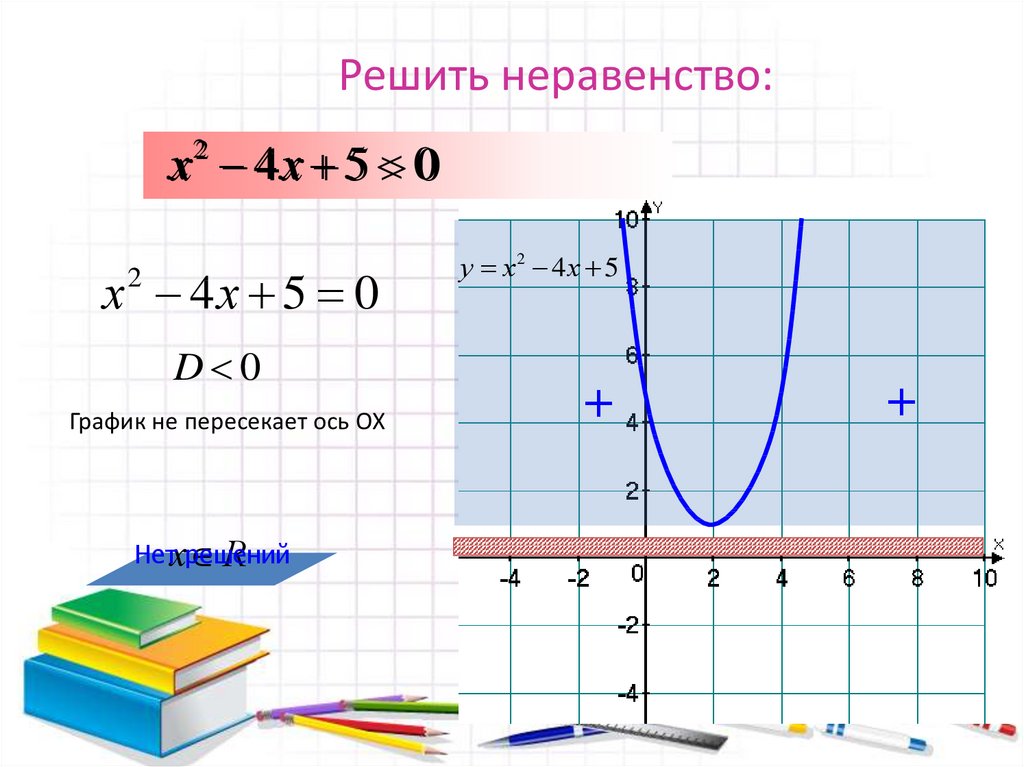
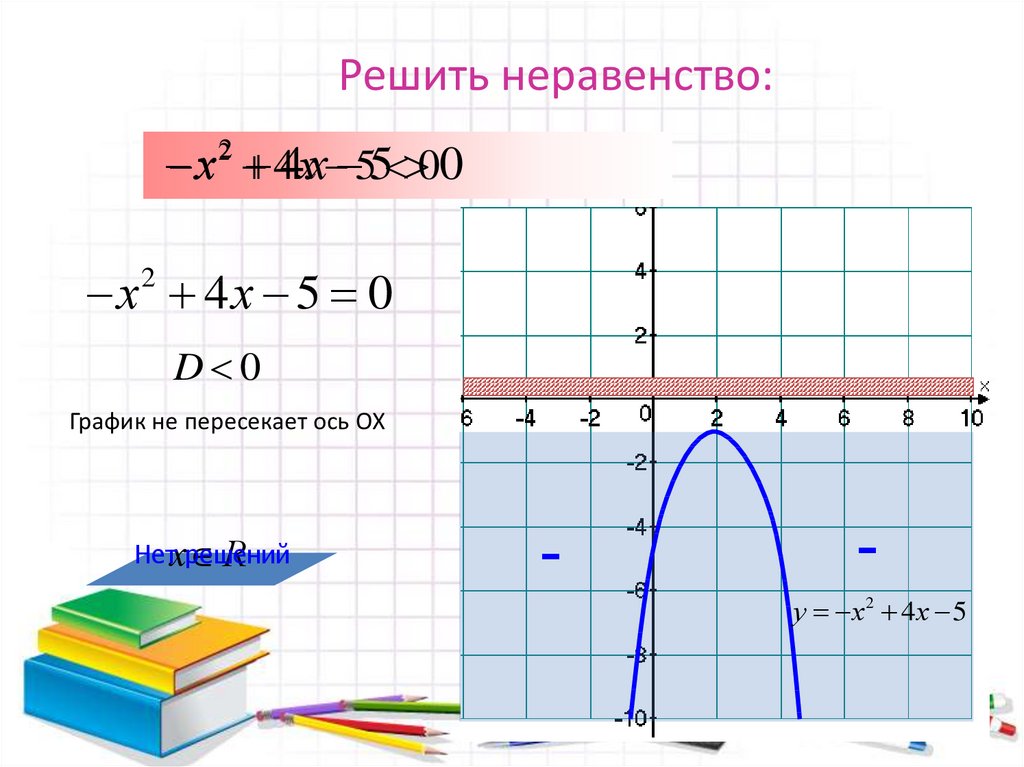
8. Решить неравенство:
х 22 4 х 5 0х 4х 5 0
2
D 0
График не пересекает ось ОХ
Нетхрешений
R
у х2 4х 5
+
+
9. Решить неравенство:
х2 44хх 55 00х 4х 5 0
2
D 0
График не пересекает ось ОХ
Нетхрешений
R
-
у х2 4х 5
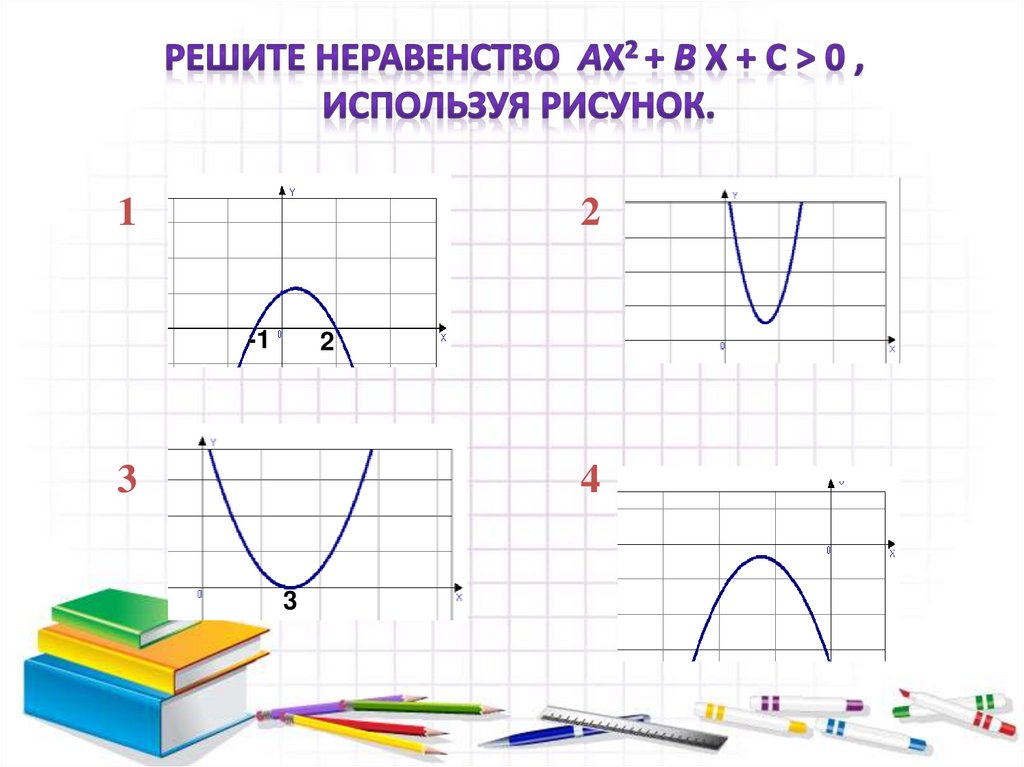
10. Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0 поступают следующим образом:
Для решения неравенств вида ах² + вх +с >0 и ах² + вх +с < 0поступают следующим образом:
• Находят дискриминант квадратного трехчлена и выясняют, имеет ли
трехчлен корни;
• Если трехчлен имеет корни, то отмечают их на оси х и через
отмеченные точки проводят схематически параболу, ветви которой
направлены вверх при а >0 или вниз при а < 0; если трехчлен не
имеет корней, то схематически изображают параболу, расположенную
в верхней полуплоскости при а >0 и в нижней при а < 0;
• Находят на оси х промежутки, для которых точки параболы
расположены выше оси х ( если решают неравенство ах² + вх +с >0
или ниже оси х (если решают неравенство ах² + вх +с < 0).
11.
12
-1
2
3
4
3
12.
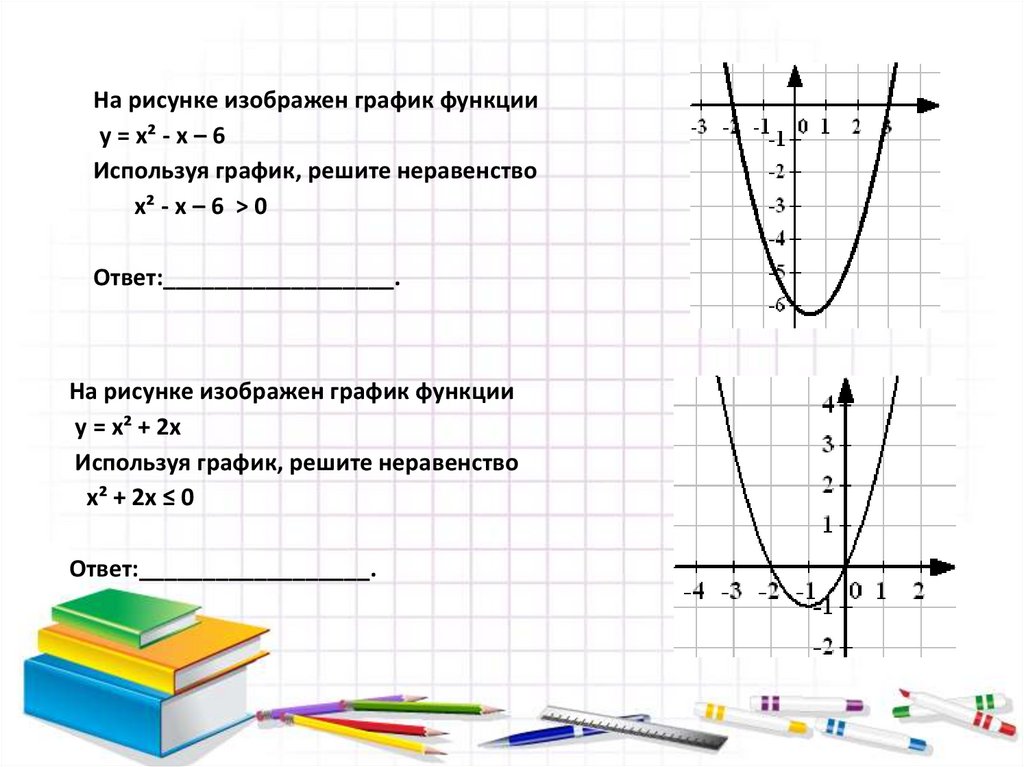
На рисунке изображен график функцииу = х² - х – 6
Используя график, решите неравенство
х² - х – 6 ˃ 0
Ответ:__________________.
На рисунке изображен график функции
у = х² + 2х
Используя график, решите неравенство
х² + 2х ≤ 0
Ответ:__________________.


 mathematics
mathematics








