Similar presentations:
Column design as Per BS 8110-1:1997
1. Column design as Per BS 8110-1:1997
PHK/JSN2. Contents :-
Contents : General Recommendations of the codeClassification of columns
Effective Length of columns & Minimum
eccentricity
Design Moments in Columns
Design
3. General Reco’s of the code
gm for concrete 1.5, for steel 1.05Concrete strength – CUBE STRENGTH
Grades of steel Fe250 & Fe460
Primary Load combination 1.4DL+1.6LL
E of concrete Ec = 5.5√fcu/ gm
10% less than IS
Ultimate stress in concrete 0.67fcu/ gm
Steel Stress-strain curve – Bilinear
E of steel 200 kN/mm2
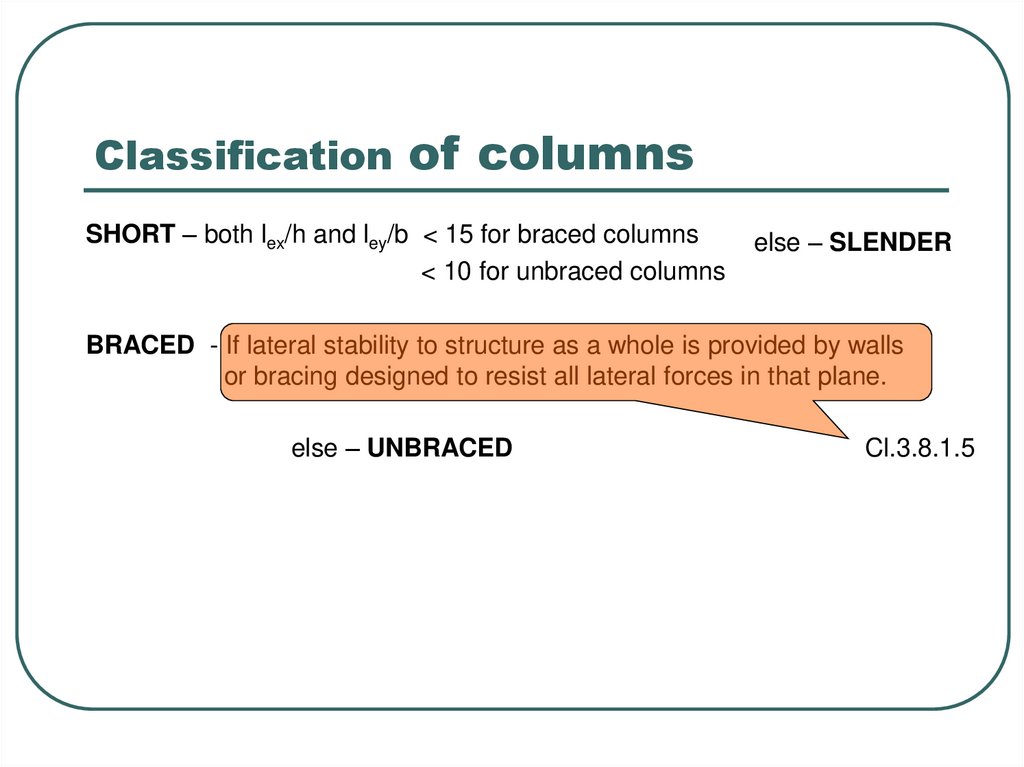
4. Classification of columns
SHORT – both lex/h and ley/b < 15 for braced columns< 10 for unbraced columns
else – SLENDER
BRACED - If lateral stability to structure as a whole is provided by walls
or bracing designed to resist all lateral forces in that plane.
else – UNBRACED
Cl.3.8.1.5
5. Effective length &minimum eccentricity
Effective length &minimum eccentricityEffective length le = ßlo
ß – depends on end condition
at top and bottom of column.
emin = 0.05 x dimension of column in the plane of bending ≤ 20 mm
6.
Contd..Deflection induced moments in Slender columns
Madd = N au
where au = ßaKh
ßa = (1/2000)(le/b’)2
K = (Nuz – N)/(Nuz – Nbal) ≤ 1
Nuz = 0.45fcuAc+0.95fyAsc
Nbal = 0.25fcubd
Value of K found iteratively
7.
Contd..Design Moments in Braced columns :
Maximum Design Column Moment Greatest of
a) M2
b) Mi+Madd
Mi = 0.4M1+0.6M2
c)M1+Madd/2
d) eminN
Columns where le/h exceeds 20 and only Uniaxially bent Shall be
designed as biaxially bent with zero initial moment along other axis.
8.
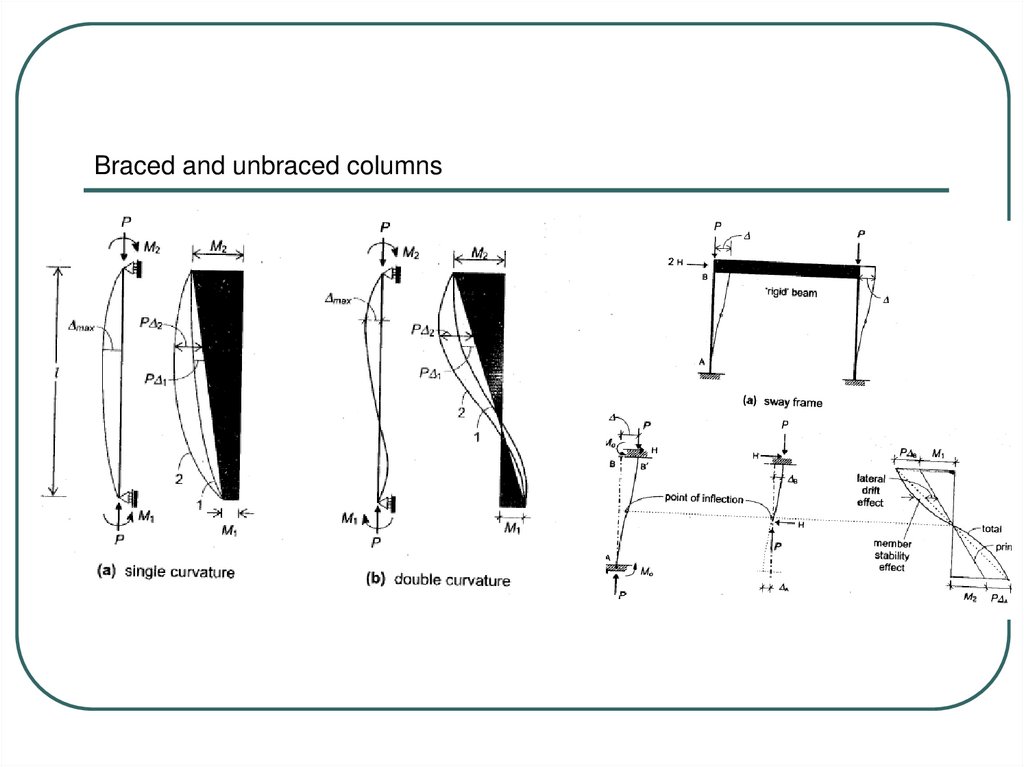
Braced and unbraced columns9.
10.
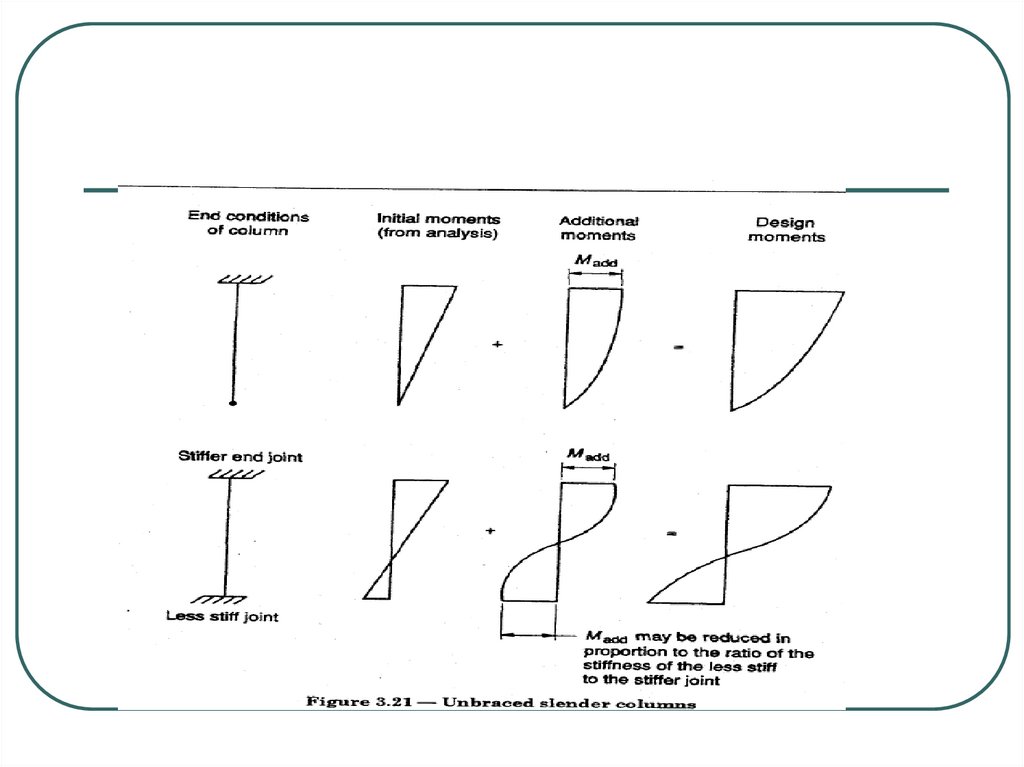
Design Moments in UnBraced columns :The additional Moment may be assumed to occur at whicheverend of column has stiffer joint. This stiffer joint may be the
critical section for that column.
Deflection of all UnBraced columns in a storey
auav for all stories = Σ au/n
11.
12. Design Moments in Columns
Axial Strength of column N = 0.4fcuAc + 0.8 AscfyBiaxial Bending
Increased uniaxial moment about one axis
Mx/h’≥ My/b’
Mx’ = Mx + ß1 h’/b’My
Mx/h’≤ My/b’
My’ = My + ß1 b’/h’Mx
Where ß1 = 1- N/6bhfcu (Check explanatory hand book)
Minimum Pt =0.4% Max Pt = 6%
13. Shear in Columns
Shear strength vc’ = vc+0.6NVh/AcMTo avoid shear cracks, vc’ = vc√(1+N/(Acvc)
If v > vc’, Provide shear reinforcement
If v ≤ 0.8√fcu or 5 N/mm²
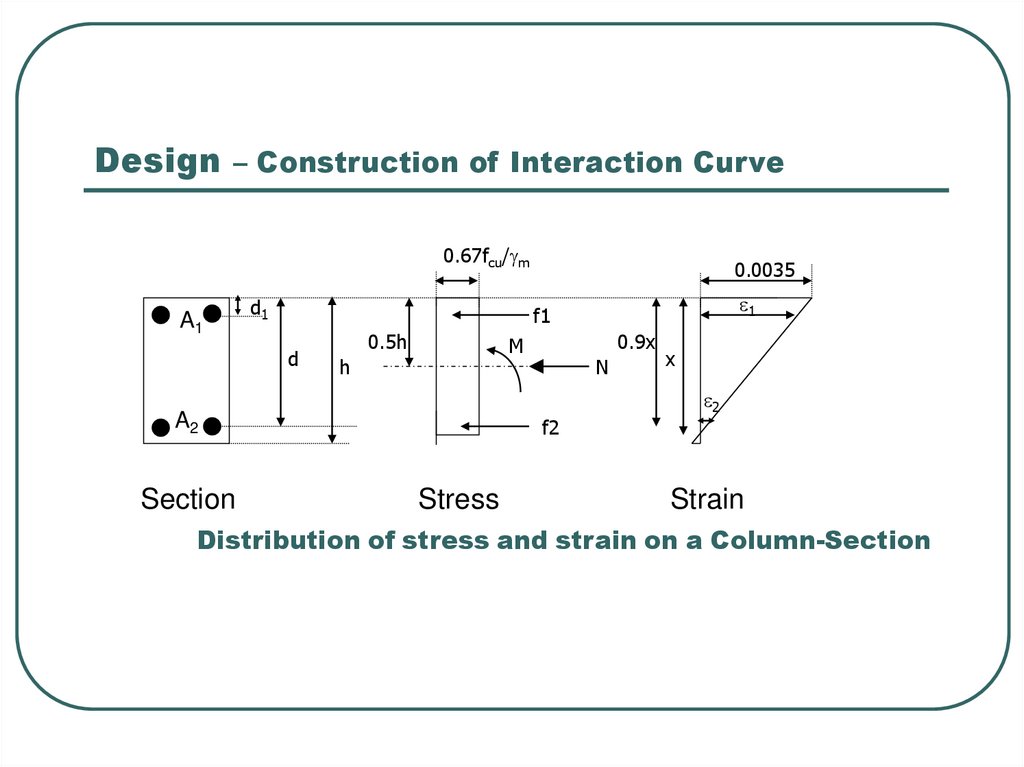
14. Design – Construction of Interaction Curve
0.67fcu/gmA1
d1
e1
f1
d
0.5h
0.9x
M
h
A2
Section
0.0035
N
f2
Stress
x
e2
Strain
Distribution of stress and strain on a Column-Section
15. Equilibrium equation from above stress block
N = 0.402fcubx + f1A1 +f2A2M =0.402fcubx(0.5h-0.45x)+f1A1(0.5h-d1)+f2A2(0.5h-d)
f1 and f2 in terms of E and
f1 = 700(x-d+h)/x
f2 = 700(x-d)/x
The solution of above equation requires trial and error method












 mathematics
mathematics








