1.38M

Category:

physics

Решение задач механики различными способами

1. Анализ текста задачи(заданного содержания), анализ
физического явления и выбор его физической модели.
2. Определение способа (идеи) решения задачи или составление
плана решения.
3. Выполнение запланированных действий (решение в общем
виде, проведение опытов и др.), получение ответа в виде
числа.
4. Анализ решения задачи. Подведение итогов.
далее
3

3.

0
Тело брошено со скоростью 15м/с под углом 30 к
горизонту. Пренебрегая сопротивлением воздуха,
определите, на какую высоту h поднимется данное тело?
y
0 х
0
0 у
h
0 х
x
далее
4

4.

1
Тело брошено со скоростью 15м/с под углом 30 к
горизонту. Пренебрегая сопротивлением воздуха,
определите, на какую высоту h поднимется данное тело?
Кинематический
Два
способа
Решение на
основе законов
кинематики
Энергетический
решения
задачи
Решение на
основе закона
сохранения
энергии
далее
5

5.

1 способ: кинематический
Решение на основе законов кинематики
1. Краткая запись условия задачи; СИ.
2. Рисунок, направление перемещения, скорости, ускорения.
3. Выбор системы координат, проекции векторов перемещения,
скорости, ускорения.
4. Запись уравнение движения тела и уравнений, связывающих
кинематические величины.
5. Решение полученной системы уравнений относительно неизвестных.
6. Анализ ответа. Если он противоречит физическому смыслу задачи, то
поиск новых идей решения.
далее
6

6.

1
Дано:
0 = 15м/с
0
= 30
h ?
Тело брошено со скоростью 15м/с под углом 30 0 к
горизонту. Пренебрегая сопротивлением воздуха,
определите, на какую высоту h поднимется данное тело?
Решение
gt 2
h 0 y t
2
Из рисунка видно: 0 y 0 sin
0 y 0 0 sin
y 0 y gt t
,
g
g
т.к. y 0
h 0 sin
0 sin
g
g 02 sin 2 02 sin 2
2
2g
2g
15 2 м / с sin 30 2
h
2,8 м
2
2 10 м / с
2
далее
7

7.

2 способ: энергетический
Решение на основе закона сохранения энергии
1. Краткая запись условия задачи; СИ.
2. Чертеж, на котором показать начальное и конечное состояние
тела или системы тел, указать, какой энергией обладало тело в
каждом состоянии.
3. Запись закона сохранения или изменения энергии и других
необходимых уравнений.
4. Решение уравнения в общем виде.
5. Проверка по размерности, выполнение расчетов, оценка
достоверность результата, запись ответа.
далее
8

8.

1
Тело брошено со скоростью 15м/с под углом 30 0 к
горизонту. Пренебрегая сопротивлением воздуха,
определите на какую высоту h поднимется данное тело?
Решение
Дано:
0 = 15м/с Нулевой уровень энергии свяжем с точкой
0
m 02
= 30
броска.
h ?
E k1
,
m 2
В верхней точке параболы: E k 2
, E р 2 mgh,
2
2
По закону сохранения энергии:
m 02 m 2
mgh, х 0 cos ,
2
2
02 2 02 02 cos 2 02 sin 2
h
2g
2g
2g
15 2 м / с sin 2 30 0
h
2,8 м
2
2 10 м / с
2
далее
9

9.

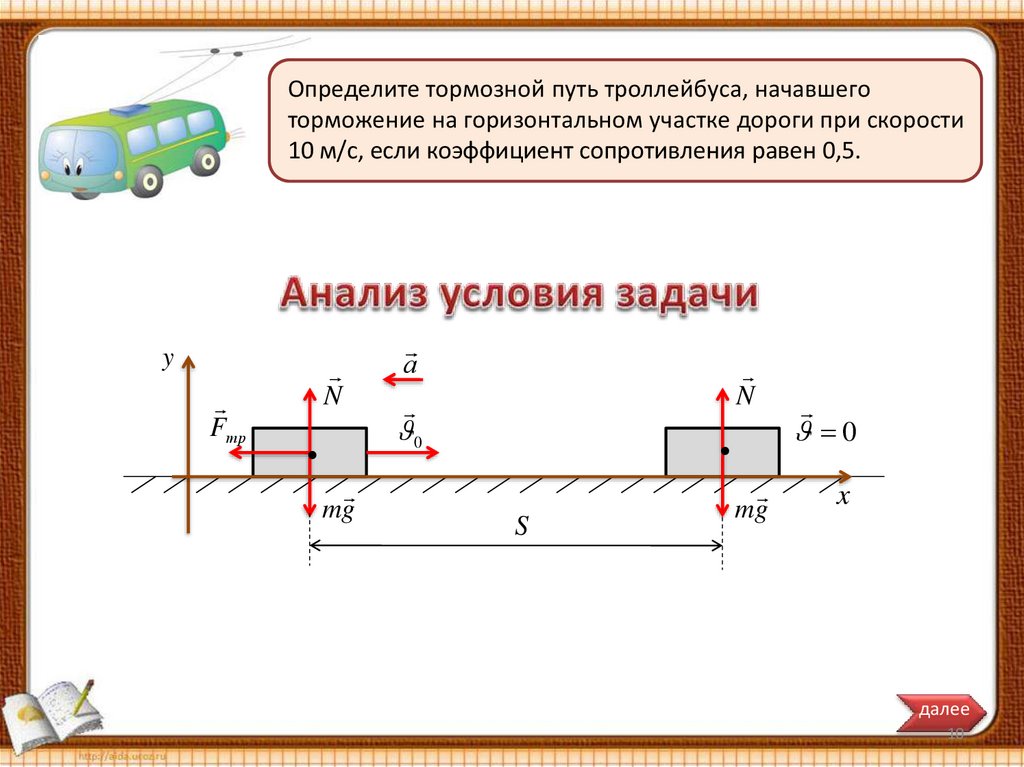
Определите тормозной путь троллейбуса, начавшего
торможение на горизонтальном участке дороги при скорости
10 м/с, если коэффициент сопротивления равен 0,5.
y
Динамический
Fтр
Решение на
основе законов
Ньютона
N
а
N
0
Энергетический
0
mg
S
mg
x
назад
далее
10

10.

2
Определите тормозной путь троллейбуса, начавшего
торможение на горизонтальном участке дороги при скорости
10 м/с, если коэффициент сопротивления равен 0,5.
Динамический
Два
способа
Решение на
основе законов
Ньютона
Энергетический
решения
задачи
Решение на
основе закона
сохранения
энергии
далее
11

11.

1 способ: динамический
Решение на основе законов Ньютона
1. Краткая запись условия; СИ.
2. Чертеж. Направление сил, ускорения.
3. Выбор системы координат.
4. Запись второго закона Ньютона в векторном виде.
5. Запись второго закона Ньютона в проекциях на оси X и Y.
6. Решение системы уравнений.
7. Проверка по размерности, расчет числового ответа к задаче и
сравнение его с реальными значениями величин.
далее
12

12.

2
Дано:
0 = 10 м/с
= 0,5
=0
Определите тормозной путь троллейбуса, начавшего
торможение на горизонтальном участке дороги при скорости
10 м/с, если коэффициент сопротивления равен 0,5.
Решение
Основное
уравнение
динамики:
F ma , N mg Fтр ma
В проекциях на оси координат:
y
Fтр
Ox : Fтр ma,
Oy : N mg 0.
S ?
a
2 02
2S
mg
; Fтр N mg ,
Fтр ma,
N
а
x
N mg
02
02
mg
S
2S
2 g
(10 м / с) 2
S
10 м
2
2 0,5 10 м / с
далее
13

13.

2
Дано:
0 = 10 м/с
= 0,5
=0
S ?
Определите тормозной путь троллейбуса, начавшего
торможение на горизонтальном участке дороги при скорости
10 м/с, если коэффициент сопротивления равен 0,5.
Решение
Так как на тело действует сила
трения, применим закон
изменения механической
энергии: E k E k 0 Aтр .
Ek 0
Ek 0
x
Aтр Fтр S cos , Fтр N mg , cos180 0 1,
Aтр mgS ,
m 02
m 2
m 2 m 02
Ek
, Ek Ek 0
,
2
2
2
2
m 02
02
mgS S
2
2 g
далее
14

14.

3
Дано:
m = 1000 т
S =5м
0 = 0
F = 14 кH
= 0,4
Определите скорость тела массой 1000 т, которую оно
наберет, пройдя расстояние 5 м без начальной скорости,
под действием (горизонтальной) силы тяги 14 кН, если сила
сопротивления составляет 40% от силы тяжести.
Динамический
способ
решение
Энергетический
способ
решение
?
далее

15.

3
Дано:
m = 1000 т
S =5м
0 = 0
F = 14 кH
= 0,4
Определите скорость тела массой 1000 т, которую оно
наберет, пройдя расстояние 5 м без начальной скорости,
под действием (горизонтальной) силы тяги 14 кН, если сила
сопротивления составляет 40% от силы тяжести.
СИ
Решение
Основное уравнение
F
m
a
,
динамики:
10 6 кг
N mg F Fтр ma
y
Fс
14 10 H В проекциях на оси
6
mg
координат:
Ox : F Fc ma,
Oy : N mg 0.
?
a
2 02
2S
;
F Fc m
2
2S
N
а
F
x
Fc mg,
2S F 0,4mg
m
10 м / с
назад

16.

3
Дано:
m = 1000 т
S =5м
0 = 0
F = 14 кH
= 0,4
?
Определите скорость тела массой 1000 т, которую оно
наберет, пройдя расстояние 5 м без начальной скорости,
под действием (горизонтальной) силы тяги 14 кН, если сила
сопротивления составляет 40% от силы тяжести.
СИ
Решение
6
Так как на тело действует
10 кг
сила трения, применим
закон изменения
6
14 10 H механической энергии:
Fс
N
Ek Ek 0 AFтр AF AN Amg
а
Ek 0 0
F
Ek
mg
Aтр 0,4mgS cos180 0 0,4mgS, Fc mg,
AF FS cos 0 0 FS , Aтg mg cos 2700 0
AN NS cos 90 0 0,
2
m 2 m 02 m
Ek Ek 0
,
2
2
2
2
m
2S F 0,4mg
FS 0,4mgS
2
m
назад
x

17.

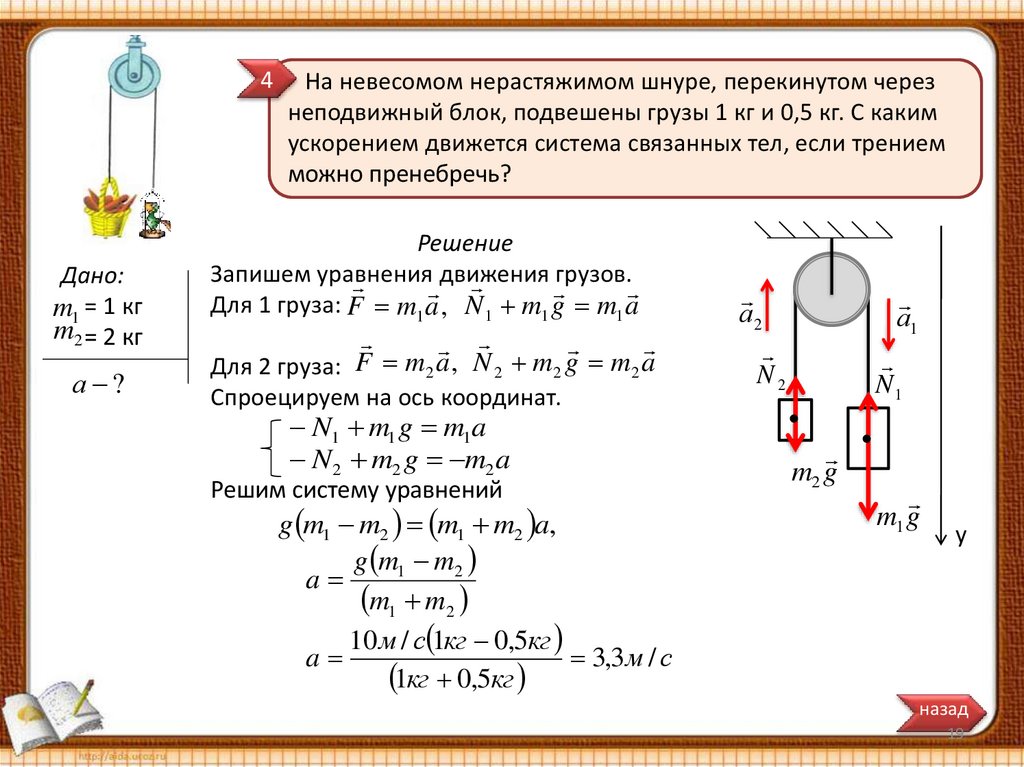
4
На невесомом нерастяжимом шнуре, перекинутом через
неподвижный блок, подвешены грузы 1 кг и 0,5 кг. С каким
ускорением движется система связанных тел, если трением
можно пренебречь?
Дано:
m1 = 1 кг
m2 = 2 кг
а ?
Динамический
способ
решение
Энергетический
способ
решение
далее
18

18.

4
Дано:
m1 = 1 кг
m2 = 2 кг
а ?
На невесомом нерастяжимом шнуре, перекинутом через
неподвижный блок, подвешены грузы 1 кг и 0,5 кг. С каким
ускорением движется система связанных тел, если трением
можно пренебречь?
Решение
Запишем уравнения
движения грузов.
Для 1 груза: F m1 a , N 1 m1 g m1 a
Для 2 груза: F m 2 a , N 2 m2 g m2 a
Спроецируем на ось координат.
N1 m1 g m1a
N 2 m2 g m2 a
Решим систему уравнений
g m1 m2 m1 m2 a,
g m1 m2
a
m1 m2
10 м / с 1кг 0,5кг
a
3,3 м / с
1кг 0,5кг
а2
а1
N2
N1
m2 g
m1 g
y
назад
19

19.

4
Дано:
m1 = 1 кг
m2 = 2 кг
а ?
На невесомом нерастяжимом шнуре, перекинутом через
неподвижный блок, подвешены грузы 1 кг и 0,5 кг. С каким
ускорением движется система связанных тел, если трением
можно пренебречь?
Решение
В отсутствии сил трения полная
механическая энергия замкнутой
системы тел не изменяется:
0 E p1 E p 2 E k1 E k 2 ,
E p2
Eк 2
m1 2 m2 2
E p1
m1 gh m2 gh
0. (1)
2
2 2
2
Eк1
2
2
0 0 h a
h
, 0
2a
2h
2a
2
m m2 g
2 m1 m2
Из уравнения (1):
h m1 m2 g
1
m1 m2
2
2h
g m1 m2
a
m1 m2
h
0
h
назад
20

20.

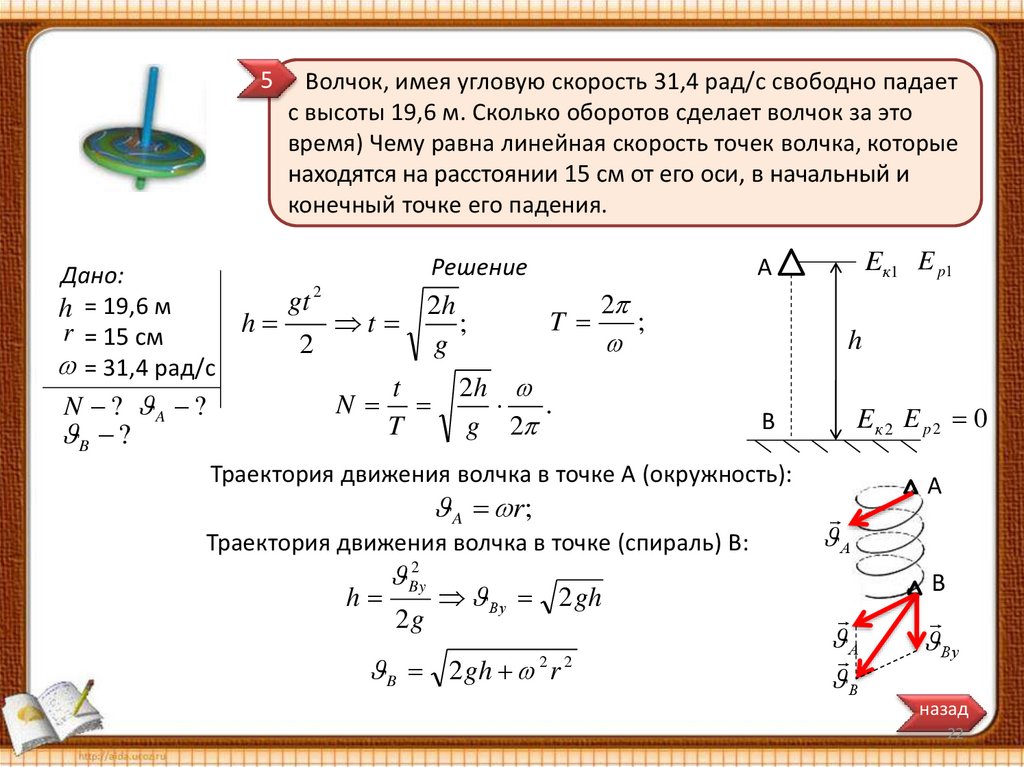
5
Волчок, имея угловую скорость 31,4 рад/с свободно падает
с высоты 19,6 м. Сколько оборотов сделает волчок за это
время) Чему равна линейная скорость точек волчка, которые
находятся на расстоянии 15 см от его оси, в начальный и
конечный точке его падения.
Дано:
h = 19,6 м
r = 15 см
= 31,4 рад/с
N ? A ?
B ?
Кинематический
способ
решение
Энергетический
способ
решение
далее
21

21.

5
Волчок, имея угловую скорость 31,4 рад/с свободно падает
с высоты 19,6 м. Сколько оборотов сделает волчок за это
время) Чему равна линейная скорость точек волчка, которые
находятся на расстоянии 15 см от его оси, в начальный и
конечный точке его падения.
Дано:
gt 2
h = 19,6 м
h
t
r = 15 см
2
= 31,4 рад/с
N ? A ?
B ?
N
Решение
2h
;
g
t
T
Eк1 E p1
А
T
2
;
2h
.
g 2
h
Eк 2 E p 2 0
В
Траектория движения волчка в точке А (окружность):
A r;
Траектория движения волчка в точке (спираль) В:
h
2
By
2g
А
Ву 2 gh
B 2 gh r
2
2
А
В
А
В
Ву
назад
22

22.

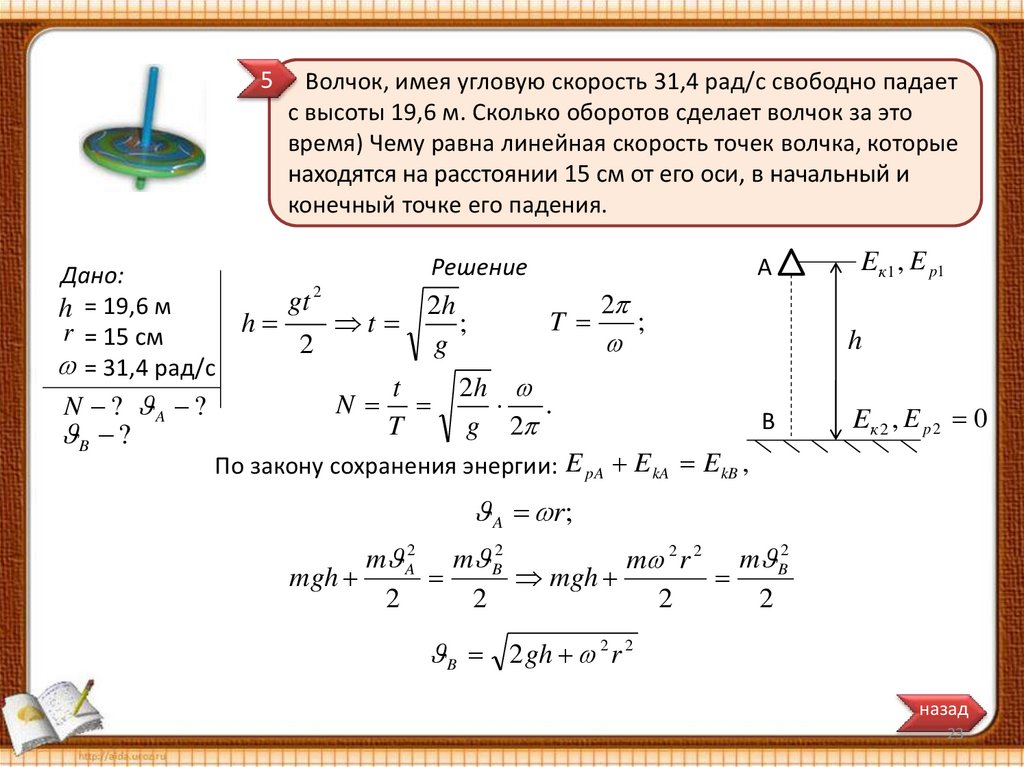
5
Волчок, имея угловую скорость 31,4 рад/с свободно падает
с высоты 19,6 м. Сколько оборотов сделает волчок за это
время) Чему равна линейная скорость точек волчка, которые
находятся на расстоянии 15 см от его оси, в начальный и
конечный точке его падения.
Дано:
gt 2
h = 19,6 м
h
t
r = 15 см
2
= 31,4 рад/с
N ? A ?
B ?
N
Решение
2h
;
g
t
T
А
T
2
;
2h
.
g 2
E к1 , E p1
h
В
Eк 2 , E p 2 0
По закону сохранения энергии: E pA E kA E kB ,
A r;
m A2 m B2
m 2 r 2 m B2
mgh
mgh
2
2
2
2
B 2 gh 2 r 2
назад
23

23.

1
Камень падает с высоты 5 м. Пренебрегая
сопротивлением воздуха, определите время падения и
конечную скорость камня.
2
Два тела одинаковой массой соединены нерастяжимой
нитью, перекинутой через блок. Одно из тел без трения
скользит по наклонной плоскости с углом у основания 300.
Определите ускорение тел. Массами блока и нитей
пренебречь.
Кинематический
или динамический
способ
решение
1 вариант
Энергетический
способ
решение
2 вариант
далее
24

24.

Дано:
h =5м
Решение кинематическим способом
h
t ? ?
h
gt 2
2
2 02
2а
t
2
2g
А
2h
;
g
2 gh
E p1 , Eк1 0
h
В
Eк 2 , E p 2 0
Решение энергетическим способом
h
gt 2
2
t
2h
;
g
m 2
E pA E kB , mgh
2 gh
2
h 1с, 10 м / с
далее
25

25.

Дано:
=300
а ?
Решение динамическим способом
1. Движение по наклонной плоскости.
F mа1 , N1 mg Fн ma1
Ox1 : mg sin Fн ma1 ,
y1
N1
Fн
а2
Fн
x1
mg
mg
а1
2. Движение по вертикали.
F mа 2 , mg Fн ma2
Oy 2 : mg Fн ma2 Fн mg ma2
mg sin mg ma2 ma1 , a1 a 2 a a
Решение энергетическим способом
0 E p1 E p 2 E k1 E k 2 ,
m 2 m 2
mgh sin mgh
.
2
2
gh 1 sin 2
2 02
2
2
a
h
, 0 0 h
2a
2h
2a
g 1 sin
a
, а 2,5 м / с 2
2
y2
g 1 sin
2
h
h sin
h
далее
26

26.

Решение
задач части
В ЕГЭ
задачи
Решение
задач части
С ЕГЭ
задачи
далее
27

27.

6
Санки с грузом 200 кг скатываются с горки под углом 14 к
горизонту. Длина спуска 60 м, коэффициент трения скольжения
саней 0,14. Определите, на какое расстояние по горизонтали
прокатятся санки после спуска до полной остановки. Считать ,
что на переходе от наклонной плоскости к горизонтали трение
отсутствует.)
Дано:
m = 200 кг
L = 60 м
0 = 0
= 0,14
= 0,4
Динамический
способ
решение
Энергетический
способ
решение
S ?
далее
28

28.

6 Санки с грузом 200 кг скатываются с горки под углом 14 к
горизонту. Длина спуска 60 м, коэффициент трения скольжения
саней 0,14. Определите, на какое расстояние по горизонтали
прокатятся санки после спуска до полной остановки. Считать ,
что на переходе от наклонной плоскости к горизонтали трение
отсутствует.)
Дано:
m = 200 кг
L = 60 м
0 = 0
= 0,14
= 0,4
S ?
Решение
1. Движение по наклонной
F
m
а
плоскости.
1,
y2 а2
N2
x1
N1 mg Fтр1 ma1
Fтр 2
x
2
Ox1 : mg sin Fтр1 ma1 ,
S
Oy1 : N mg cos 0.
mg
N mg cos , Fтр1 N mg cos
S
2 02
2a
a
y1
а
N1 1
Fтр1
mg
12 02
2L
mg sin mg cos m
12
2L
2Lg (sin cos )
,
2
1
далее
29

29.

6 Санки с грузом 200 кг скатываются с горки под углом 14 к
горизонту. Длина спуска 60 м, коэффициент трения скольжения
саней 0,14. Определите, на какое расстояние по горизонтали
прокатятся санки после спуска до полной остановки. Считать ,
что на переходе от наклонной плоскости к горизонтали трение
отсутствует.)
Дано:
m = 200 кг
L = 60 м
0 = 0
= 0,14
= 300
S ?
а
N1 1
Решение
2. Движение
по горизонтали.
N 2 y1
а
F
m
а
,
y
2 2
2
N 2 mg Fтр 2 ma 2
Fтр 2
x2
Ox 2 : Fтр 2 ma2 ,
S
Oy 2 : N mg 0.
mg
Fтр 2 N mg, mg ma a g
S
2 02
a
22 12
. Так как 2 0, a
x1
Fтр1
mg
12
2S
2S
2Lg (sin cos ) L(sin cos )
g
S
2S
2 g
2 g
60 м(sin 30 0 0,14 cos 30 0 )
S
162,3 м
назад
0,14
2a
2
1
2
1
30

30.

6 Санки с грузом 200 кг скатываются с горки под углом 14 к
горизонту. Длина спуска 60 м, коэффициент трения скольжения
саней 0,14. Определите, на какое расстояние по горизонтали
прокатятся санки после спуска до полной остановки. Считать ,
что на переходе от наклонной плоскости к горизонтали трение
отсутствует.)
Дано:
m = 200 кг
L = 60 м
0 = 0
= 0,14
= 0,4
S ?
Решение
В качестве нулевого уровня
отсчета потенциальной энергии
выберем горизонтальную
плоскость. По закону сохранения
энергии: E p1 Aтр1 Aтр 2 ;
S
E p1 mgh ; Aтр1 Fтр1 L mg cos L;
Aтр 2 Fтр 2 S mgS;
mgh mg cos mgS;
S
y1
N1
x1
Fтр1 E p1
Fтр 2
L
h
Eк1
h L sin ;
L(sin cos )
назад
31

31.

далее
32

32.

7 По гладкой горизонтальной направляющей длины 2L скользит бусинка с
положительным зарядом Q > 0 и массой m. На концах направляющей находятся
положительные заряды q > 0. Бусинка совершает малые колебания относительно
+q
+q
положения равновесия, период которых равен Т.
+Q, m
Во сколько раз следует уменьшить заряд бусинки, чтобы период ее колебаний
увеличился в 3 раза?
Дано:
m, 2 L
q, Q
T2 3T1
q1
?
q2
1. Сместим бусинку на малое расстояние от
+q
+Q, m
положения равновесия.
2. На бусинку действуют кулоновские силы со
x
стороны зарядов +q.
3. Так как F рез 0 , появилось ускорение, но оно переменное.
4. Бусинка начинает совершать гармонические колебания.
+q
x
x хmax cos t ,
x хmax sin t ,
a x 2 x max cos t 2 x, a 2 x 0.
2
5. Период колебаний можно выразить через : T
;
6. Частоту можно найти из уравнения ускорения или скорости тела.
7. Выразив частоту, найдем искомую величину.
далее
33

33.

34.

Рассмотрим знаменатель. По условию x L L x L x L
L x 2 L x 2 L4
Рассмотрим числитель.
L x 2 L x 2 L2 2 Lx x 2 L2 2 Lx x 2 4 Lx
4kqQ
mа 3 x
L
или
4kqQ
4kqQ
а
x 0
а
x
3
3
mL
mL
Получили уравнение гармонических колебаний a 2 x 0,
4kqQ
,
3
mL
2
mL3
T
2
4kqQ
Из полученной формулы видно, чтобы период колебаний увеличился в
3 раза, заряд бусинки надо уменьшить в 9 раз.
далее
35

35.

36.

8 Полый металлический шарик массой 3 г подвешен на шелковой нити длиной
50 см над положительно заряженной плоскостью, создающей однородное
6
электрическое поле напряженностью 2∙10 В/м. Электрический заряд шарика
-8
отрицателен и по модулю равен 3∙10 Кл. Определите период свободных
гармонических колебаний маятника.
Дано:
Решение
m 3г
L 50см
Е 2 10 В / м
6
q 3 10 8 Кл
Энергетический способ
2
m max
, E p1 q 1 ;
В состоянии 1: E k1
2
В состоянии 2: Ek 2 0, E p 2 q 2 mgh;
По закону сохранения энергии:
2
m
max
Т ?
E k1
q 1 q 2 mgh;
2
2
m max
mgh q 12 1
2
Так как поле однородно 12 Eh, 2
Е
L h
g
L
2
А
h
q
+ + + + + + + +
1
Из рисунка h L L h L L cos L 1 cos L 2 sin 2 / 2
2
A2
, 3
Колебания гармонические, если угол мал sin / 2 / 2 h L
2
2L
где A L амплитуда колебаний.
далее
37

37.

Подставим уравнения (2) и (3) в уравнение (1), получим
2
m max
A2
mgh qEh mg qE ,
2
2L
max
g qE
A.
L mL
При свободных незатухающих колебаниях максимальная скорость связана
с амплитудой законом
2
max A
A,
x хmax sin t .
T
Тогда
T
2
2
mL
mg qE
3 10 3 кг 0,5 м
T 2 3,14
0,81с
3
2
8
6
3 10 кг 10 м / с 3 10 Кл 2 10 В / м
далее
38

38.

39.

Если ты умеешь правильно судить себя,
значит, ты поистине мудр.
Антуан де Сент-Экзюпери
Участвовал
в открытии
нового
Справился с
затруднением
Работа в
группе
Все получилось
(проверочная
работа)
Надо
тренироваться
Оцени свою работу на уроке по
предложенным параметрам по трех
бальной системе.
40

40.

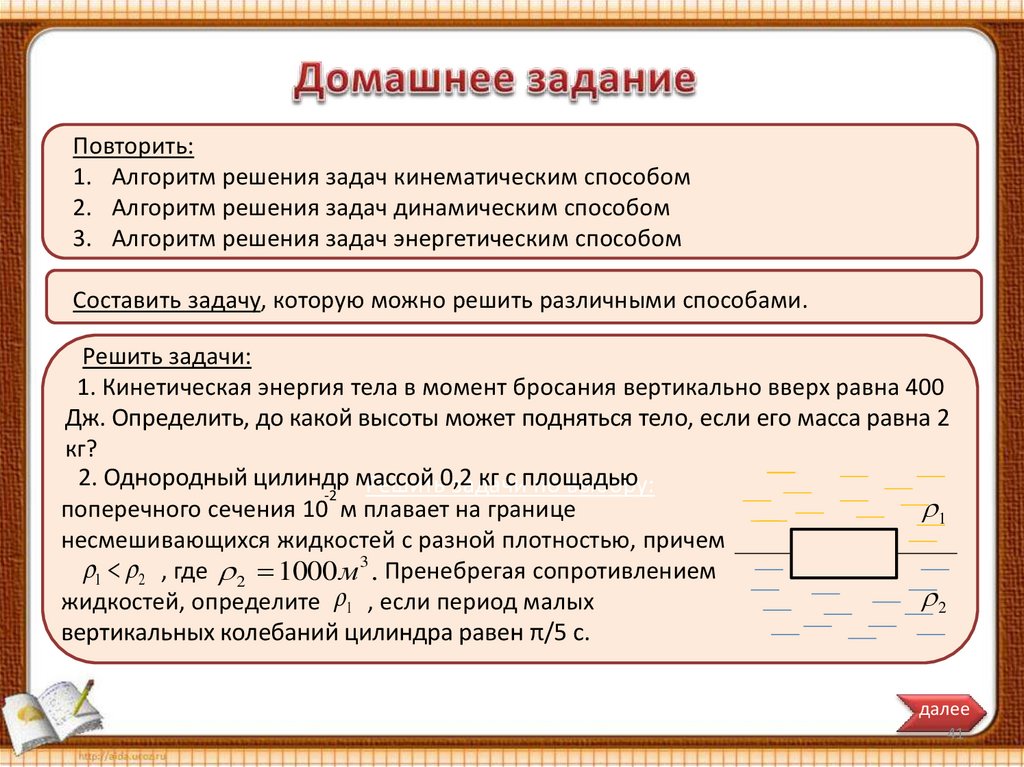
Повторить:
1. Алгоритм решения задач кинематическим способом
2. Алгоритм решения задач динамическим способом
3. Алгоритм решения задач энергетическим способом
Составить задачу, которую можно решить различными способами.
Решить задачи:
1. Кинетическая энергия тела в момент бросания вертикально вверх равна 400
Дж. Определить, до какой высоты может подняться тело, если его масса равна 2
кг?
2. Однородный цилиндр массой
кг с площадью
Решить0,2
задачи
по выбору:
-2
поперечного сечения 10 м плавает на границе
1
несмешивающихся жидкостей с разной плотностью, причем
1 2 , где 2 1000 м 3 . Пренебрегая сопротивлением
2
жидкостей, определите 1 , если период малых
вертикальных колебаний цилиндра равен π/5 с.
далее
41

41.

42.

1. Дряпина А.А. Рефлексия деятельности на уроке. Радуга успеха.
Сайт кафедры развития образовательных систем НМЦ ЮВОУО.
http://experiment.nmc.uvuo.ru/
2. Мякишев Г.Я., Буховцев Б.Б. Физика: Учебник для 10 класса
ООУ. - М.: Просвещение, 2009.
3. Орлов В.Ф. Практика решения физических задач: 10-11 классы:
учебное пособие для учащихся общеобразовательных
учреждений/ В.А. Орлов, Ю.А. Сауров. – М.: Вентана-Граф,
2010.
4. Парфентьева Н.А. Сборник задач по физике: базовый и
профил. Уровни: для 10-11 кл. общеобразоват. Учреждений/
Н.А. Парфентьева. – М.: Просвещение, 2007.
5. Фоминых О.Ю. Решение задач механики динамическим и
энергетическим способами.- Газета «Физика» №2/99
6. Шабалин Е.И. Репетитор по физике. Задачи ЕГЭ.
http://www.reppofiz.info/ege.html
43

English Русский Rules