Решение задач на применение теоремы о трех перпендикуляров и нахождение угла между прямой и плоскости

1.

14.12.
Решение задач на применение теоремы о трех
перпендикуляров и нахождение угла между прямой и
плоскости

2.

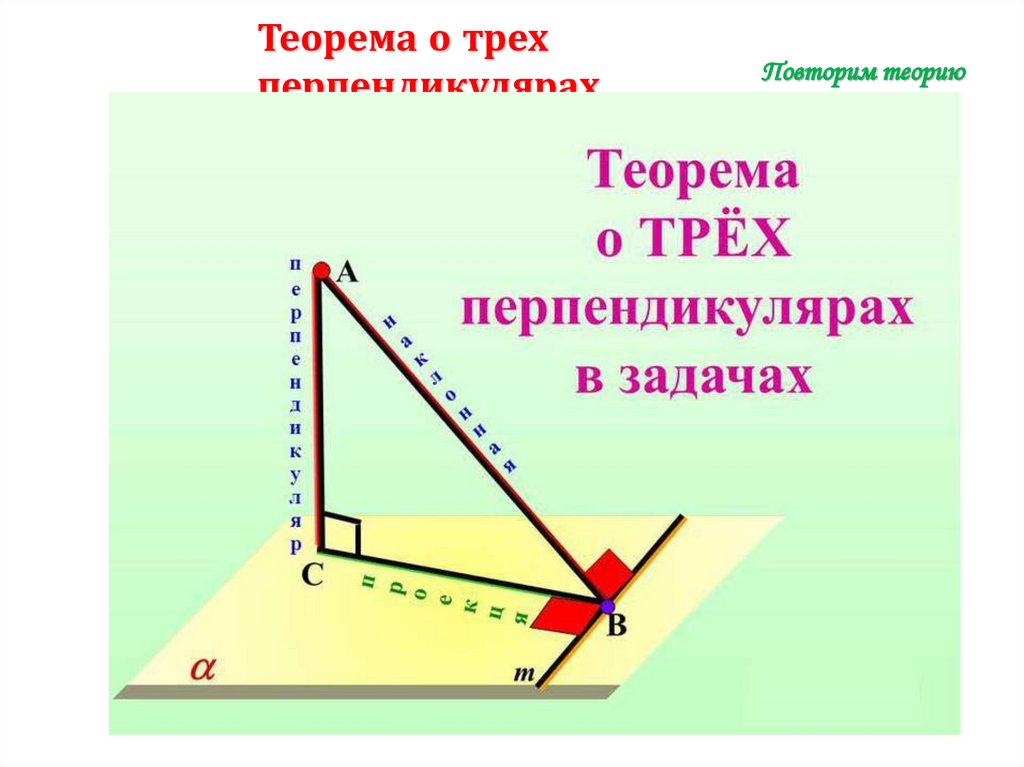
Теорема о трех
перпендикулярах.
Повторим теорию

3.

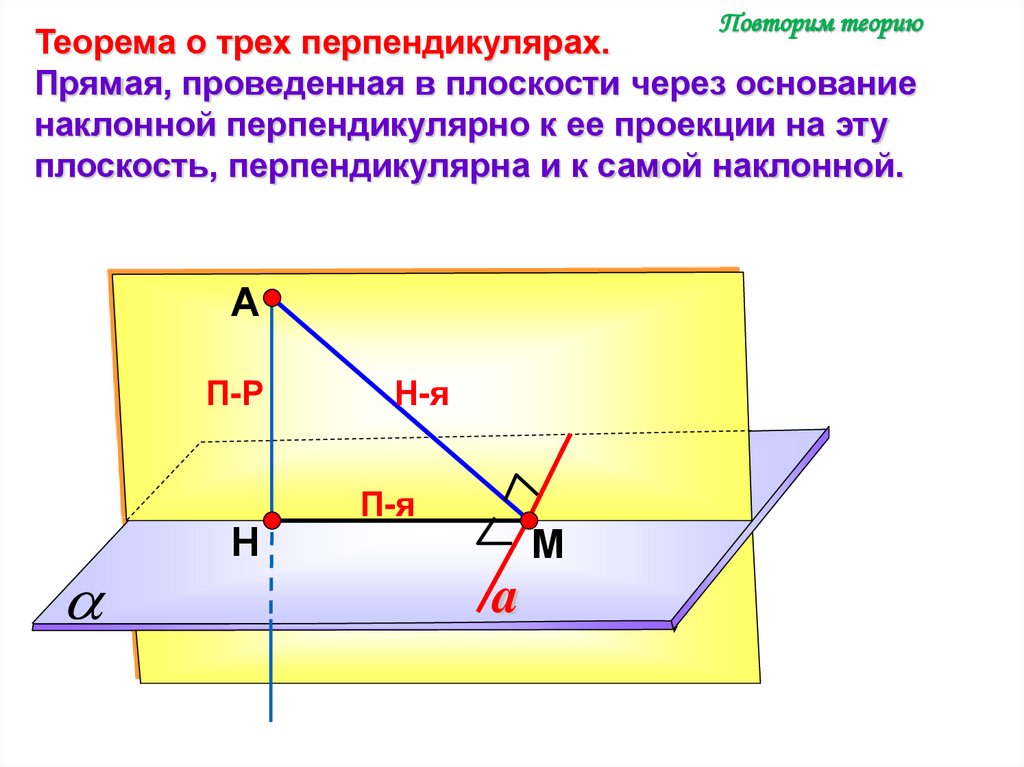
Повторим теорию
Теорема о трех перпендикулярах.
Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна и к самой наклонной.
А
П-Р
Н
Н-я
П-я
М
a

4.

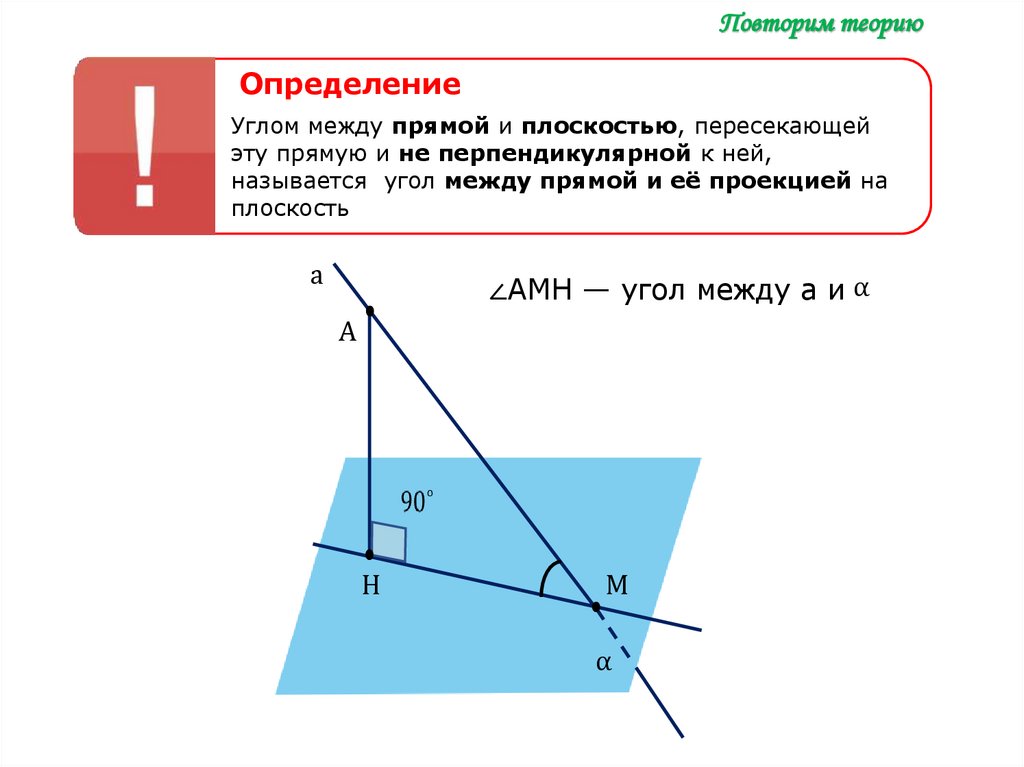
Повторим теорию
Определение
Углом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и её проекцией на
плоскость
a
∠АМH — угол между а и α
A
H
M
α

5.

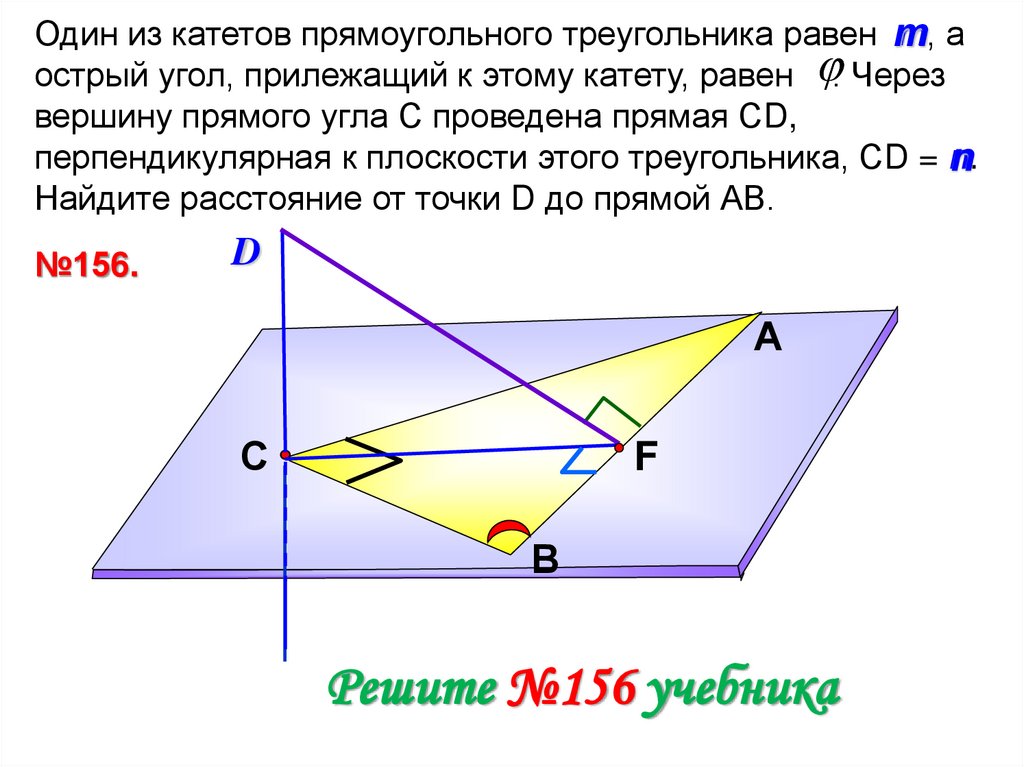
Один из катетов прямоугольного треугольника равен т
т, а
острый угол, прилежащий к этому катету, равен . Через
вершину прямого угла С проведена прямая СD,
перпендикулярная к плоскости этого треугольника, СD = n.
n
Найдите расстояние от точки D до прямой АВ.
№156.
D
А
С
F
В
Решите №156 учебника

6.

Решите задачи
Учебник геометрии: п.19-21.
1. В треугольнике АВС С = 900, А=300. Через точку С проведена прямая СМ
перпендикулярная плоскости АВС, причем АС = 18 см, СМ = 12 см. Найдите
расстояние от точки В до плоскости АСМ.
2. В параллелограмме АВСD АВ = 20 см, ВАD = 450, ВМ – перпендикуляр к
плоскости АВС, а угол между прямой МА и плоскостью параллелограмма равен
600. Найдите расстояние от точки М до плоскости АВС.

7.

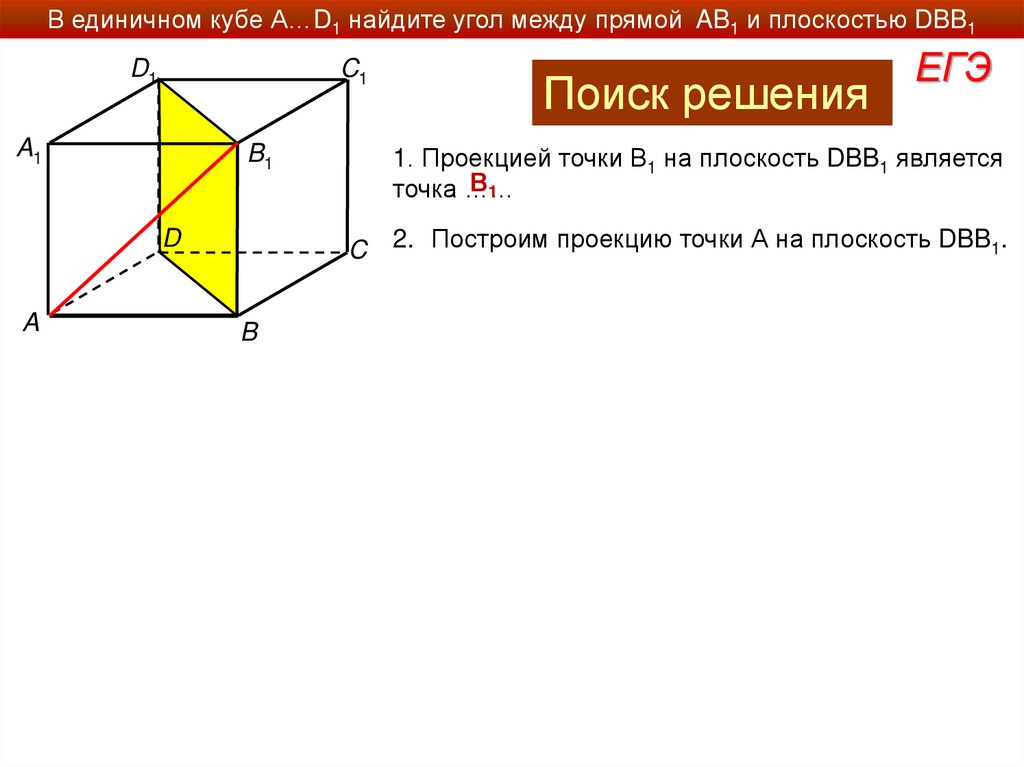
Разберите решение задачу из ЕГЭ по данной теме
В единичном кубе А…D1 найдите угол между
прямой AB1 и плоскостью DBB1.

8.

В единичном кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
B1
D
A
1. Проекцией точки В1 на плоскость DBB1 является
В1
точка ……
C
B
Поиск решения
ЕГЭ
2. Построим проекцию точки А на плоскость DBB1.

9.

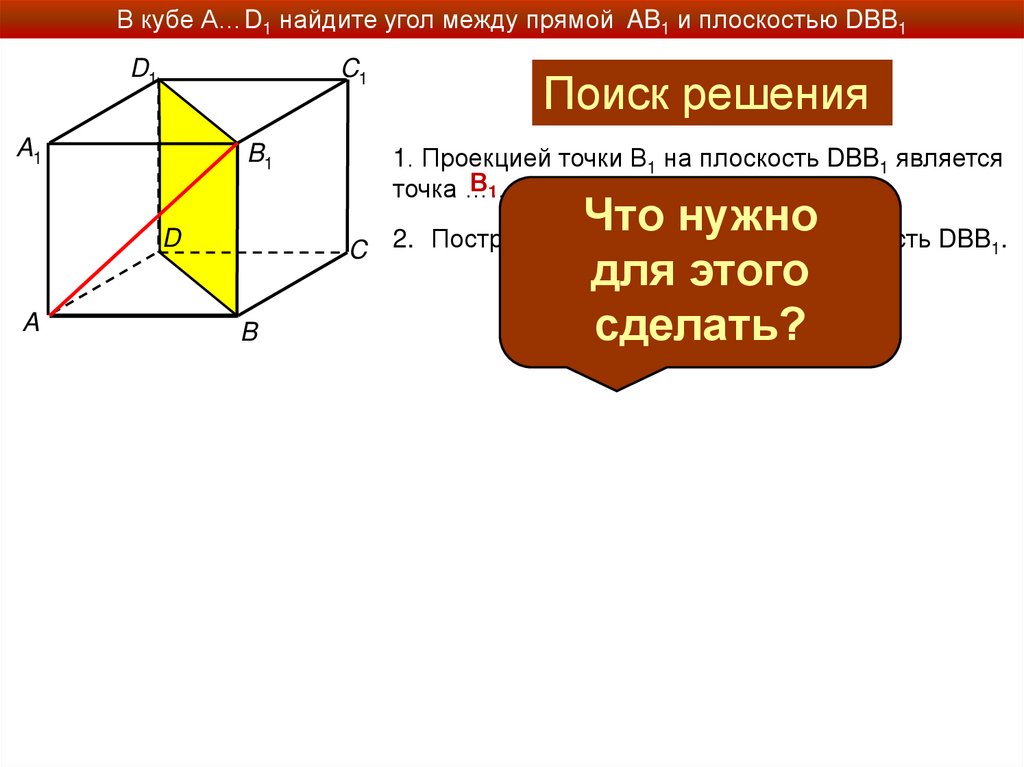
В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
B1
D
A
1. Проекцией точки В1 на плоскость DBB1 является
В1
точка ……
C
B
Поиск решения
Что нужно
для этого
сделать?
2. Построим проекцию точки А на плоскость DBB1.

10.

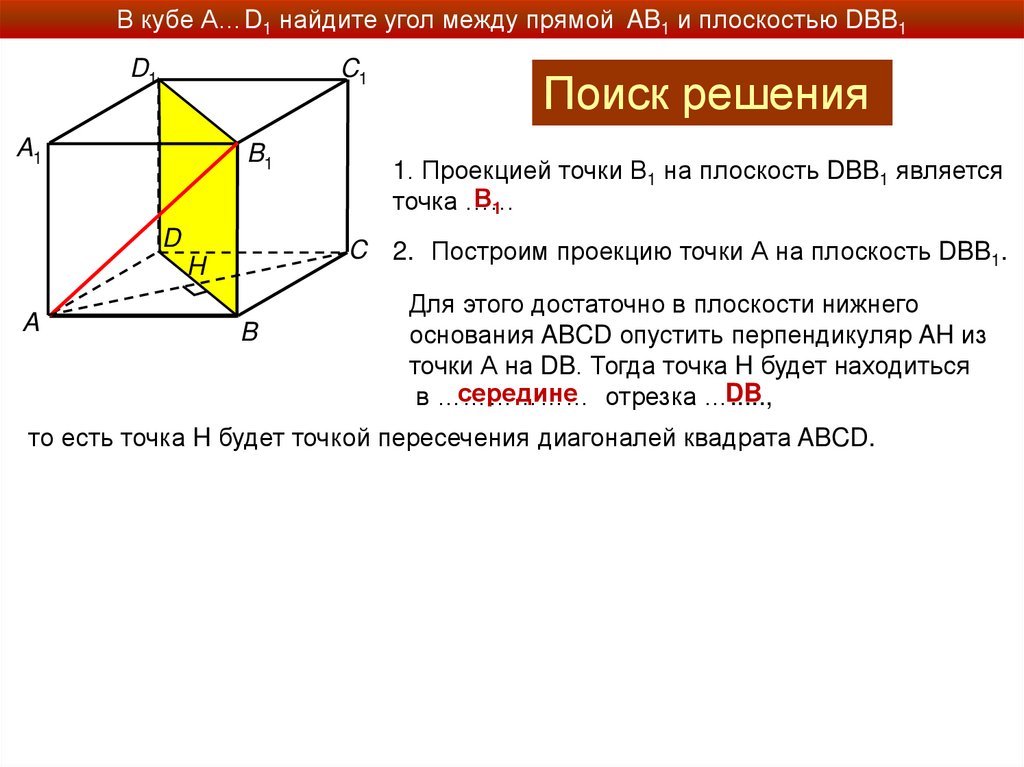
В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
B1
D
A
1. Проекцией точки В1 на плоскость DBB1 является
В1
точка ……
C
H
B
Поиск решения
2. Построим проекцию точки А на плоскость DBB1.
Для этого достаточно в плоскости нижнего
основания ABCD опустить перпендикуляр AH из
точки А на DB. Тогда точка H будет находиться
середине отрезка ….....,
DB
в ………………
то есть точка H будет точкой пересечения диагоналей квадрата ABCD.

11.

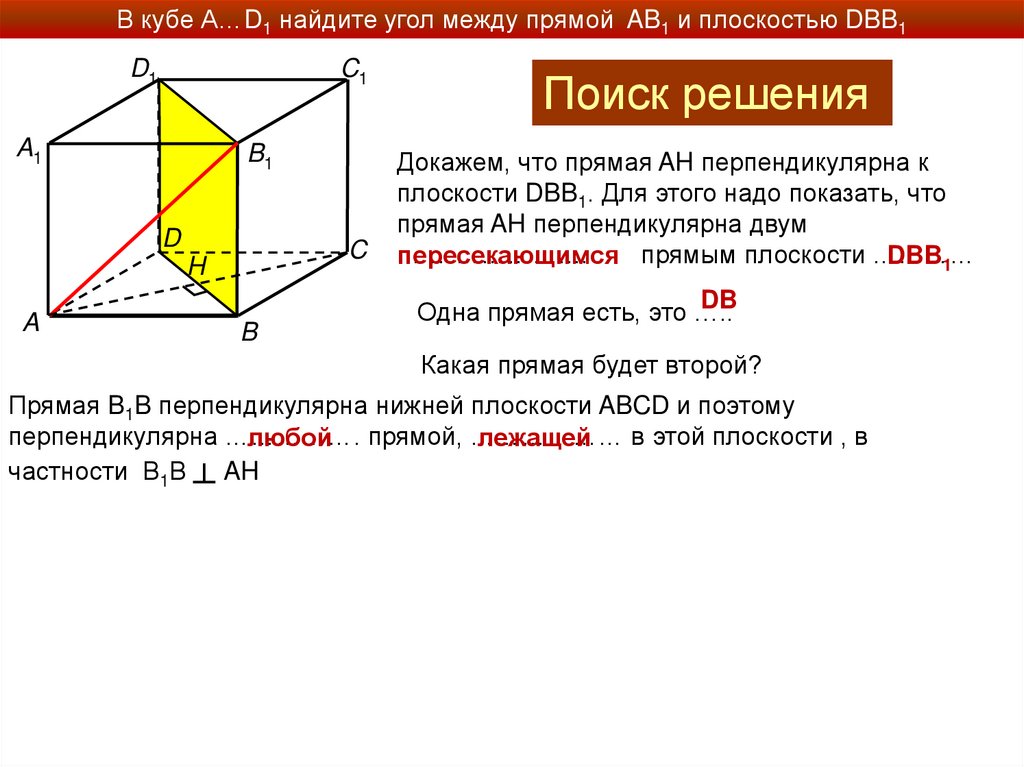
В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
B1
D
C
H
A
B
Поиск решения
Докажем, что прямая AH перпендикулярна к
плоскости DBB1. Для этого надо показать, что
прямая AH перпендикулярна двум
……………….…
прямым плоскости …………
пересекающимся
DBB1
DB
Одна прямая есть, это …..
Какая прямая будет второй?
Прямая B1B перпендикулярна нижней плоскости ABCD и поэтому
перпендикулярна …………….
в этой плоскости , в
любой прямой, ………………
лежащей
частности В1В ┴ AH

12.

В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
B1
D
C
H
A
Поиск решения
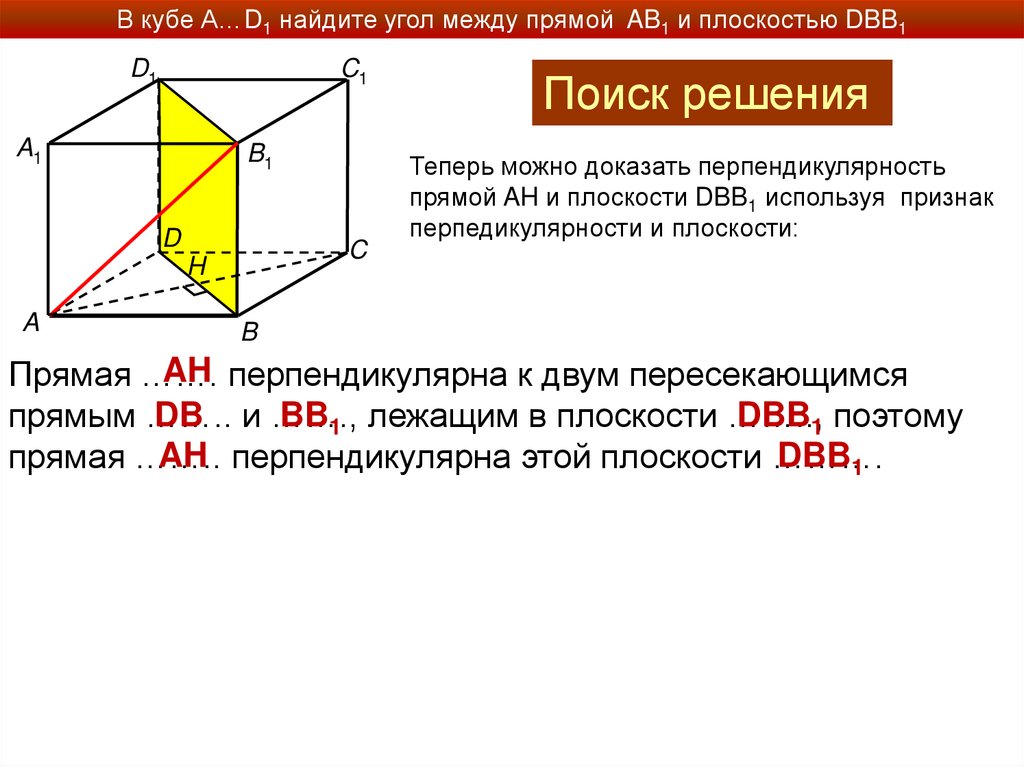
Теперь можно доказать перпендикулярность
прямой AH и плоскости DBB1 используя признак
перпедикулярности и плоскости:
B
AH перпендикулярна к двум пересекающимся
Прямая …….
DB и …….,
BB1 лежащим в плоскости ……..,
DBB1 поэтому
прямым ……..
AH перпендикулярна этой плоскости ……….
DBB1
прямая ……..

13.

В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
B1
D
C
H
A
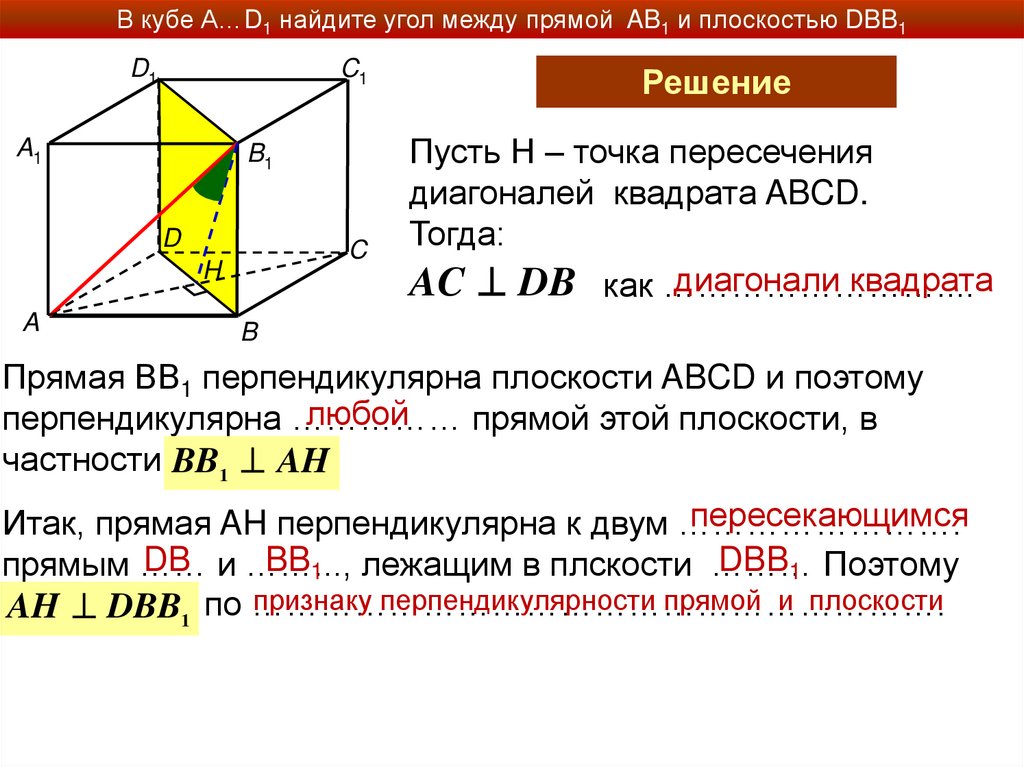
Решение
Пусть Н – точка пересечения
диагоналей квадрата ABCD.
Тогда:
диагонали квадрата
AC DB как ……………………....
B
Прямая ВВ1 перпендикулярна плоскости ABCD и поэтому
любой
перпендикулярна ……………
прямой этой плоскости, в
частности ……………
BB1 AH
пересекающимся
Итак, прямая AH перпендикулярна к двум …………………….
DB и ……...,
BB1 лежащим в плскости ………
DBB1 Поэтому
прямым ……
признаку перпендикулярности прямой и плоскости
AH DBB1 по …………………………………………………….

14.

В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
C
H
A
Так как
B1
D
B
углу AB1H-???
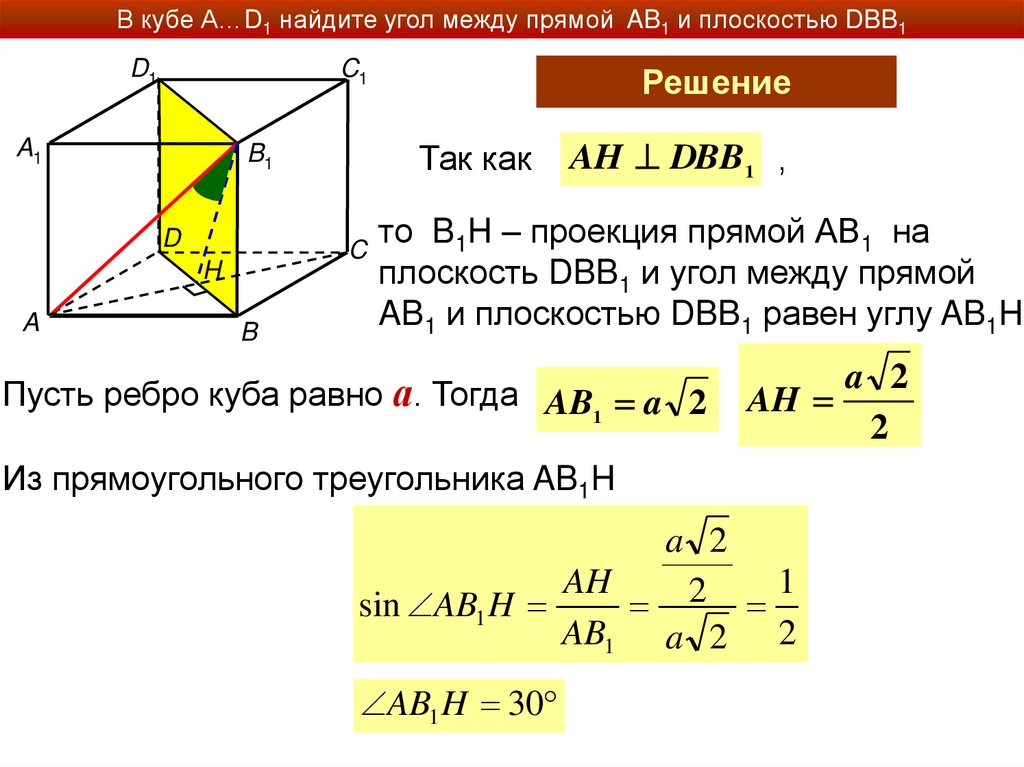
Решение
AH DBB1 ,
то B1H – проекция прямой АВ1 на
плоскость DBB1 и угол между прямой
AB1 и плоскостью DBB1 равен углу AB1H

15.

В кубе А…D1 найдите угол между прямой AB1 и плоскостью DBB1
D1
C1
A1
C
H
A
Так как
B1
D
B
Решение
AH DBB1 ,
то B1H – проекция прямой АВ1 на
плоскость DBB1 и угол между прямой
AB1 и плоскостью DBB1 равен углу AB1H
Пусть ребро куба равно а. Тогда AB1 a 2
a 2
AH
2
Из прямоугольного треугольника AB1H
a 2
AH
1
2
sin AB1 H
AB1 a 2 2
AB1 H 30