Similar presentations:
Решение задач на применение теоремы о трех перпендикуляров и нахождение угла между прямой и плоскости
1.
Работа за 19 декабря2.
19.12.Решение задач на применение теоремы о трех
перпендикуляров и нахождение угла между прямой и
плоскости
3.
I. Повторите теорию п.20,21 учебника.4.
Итак,Теорема о трех
перпендикулярах.
5.
Теорема о трех перпендикулярах.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ее проекции на эту
плоскость, перпендикулярна и к самой наклонной.
А
П-Р
Н
Н-я
П-я
М
a
6.
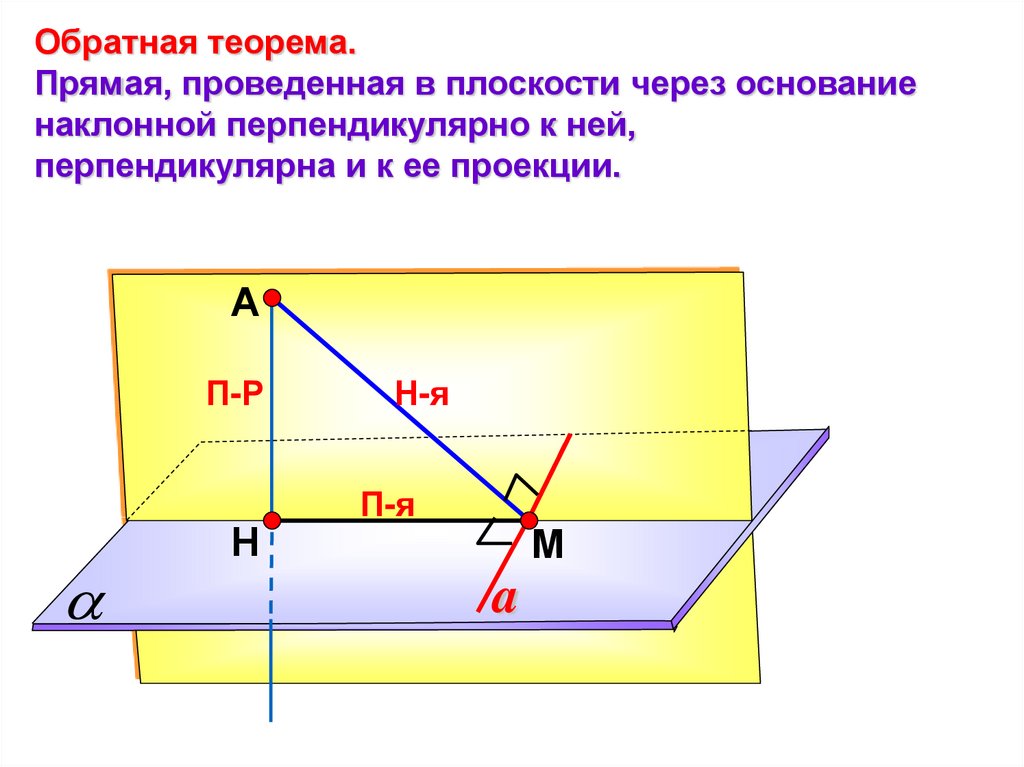
Обратная теорема.Прямая, проведенная в плоскости через основание
наклонной перпендикулярно к ней,
перпендикулярна и к ее проекции.
А
П-Р
Н
Н-я
П-я
М
a
7.
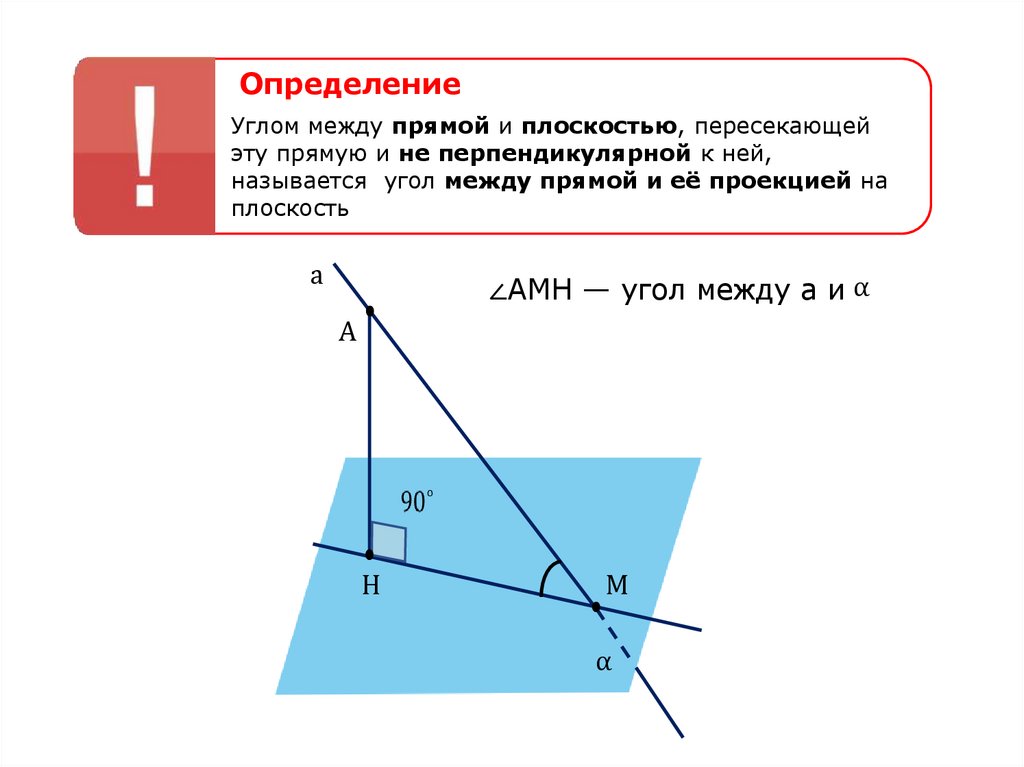
ОпределениеУглом между прямой и плоскостью, пересекающей
эту прямую и не перпендикулярной к ней,
называется угол между прямой и её проекцией на
плоскость
a
∠АМH — угол между а и α
A
H
M
α
8.
II. В тетради решите 4 задачи из этой презентации.Решение отправьте мне через электронный журнал.
9.
№1. Прямая ВF перпендикулярна к плоскости параллелограмма АВСD, ВК – высота,проведенная к стороне DC. Найдите площадь треугольника DFC, если ВF = 6 см, FК
= 10 см, SABCD = 40 см2 .
10.
№2. Из данной точки к плоскости проведены две наклонные, которые образуют сэтой плоскостью углы, равные 300, а между собой они образуют угол 600, расстояние
между основаниями данных наклонных равно 8 дм. Найдите расстояние от этой
точки до плоскости.










 mathematics
mathematics








