Similar presentations:
Описательная статистика. Лекция 2
1. ЛЕКЦИЯ 2
ОПИСАТЕЛЬНАЯСТАТИСТИКА
2. 2.1. Группировка данных
3. Обработку данных полезно начать с их группировки…
Группировка - это систематизацияпервичных данных, направленная
на извлечение заключенной в них
информации и выявление
закономерностей, которым
подчиняется изучаемое явление
или объект.
4. Группировка количественных данных :
по значениямвариант
по классам
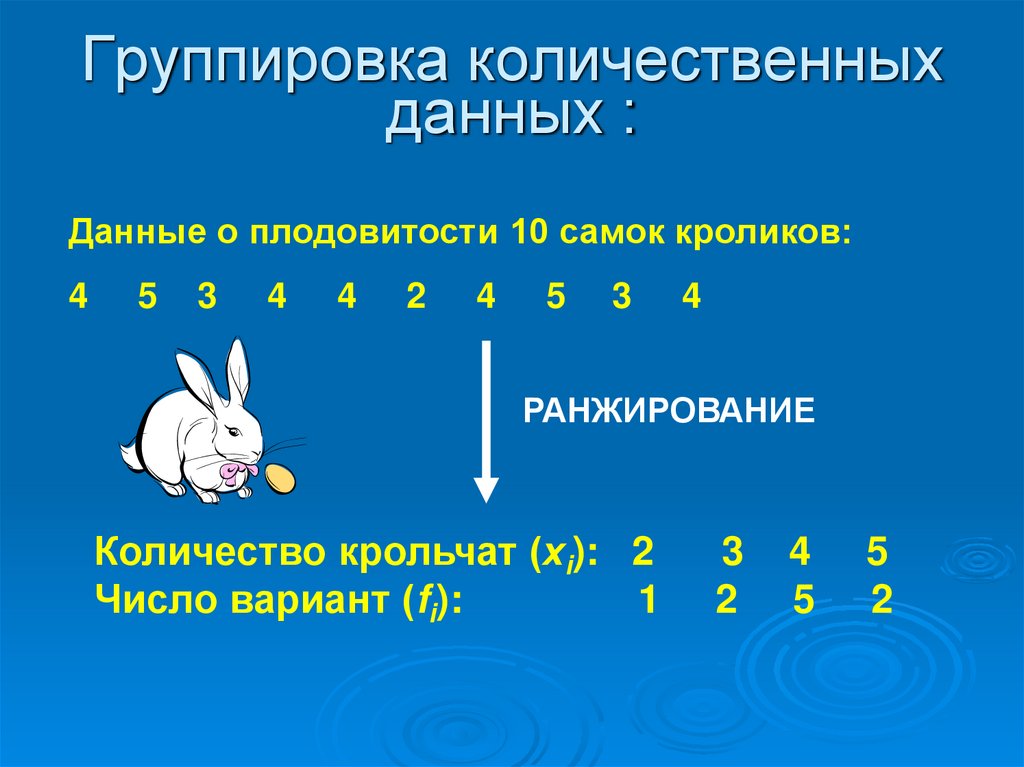
5. Группировка количественных данных :
Данные о плодовитости 10 самок кроликов:4
5
3
4
4
2
4
5
3
4
РАНЖИРОВАНИЕ
Количество крольчат (хi): 2
Число вариант (fi):
1
3
2
4
5
5
2
6.
Частота варианты (fi) - число,показывающее, сколько раз
варианта встречается в
совокупности.
Σfi=n
7.
При небольшом объеме выборкии незначительной вариации
признака, количественные данные
достаточно сгруппировать
по значениям вариант
8. Группировка данных в классы, объединяющие несколько вариант:
Применяется при больших объемахвыборок и значительной вариации
признака.
Пример: измерена длина клеток у 50
инфузорий. Полученные значения
изменялись от 60 до 120 мкм.
9.
Логично выделить классы,охватывающие несколько значений
вариант:
«60-69 мкм», «70-79 мкм», «80-89 мкм»
и т.д.
i – классовый промежуток (=интервал)
i = 10
10. Какую информацию дает вариационный ряд???
Границы изменчивости признака:минимальное и максимальное
значение вариант, или лимиты.
(Разница между лимитами называется
размахом выборки).
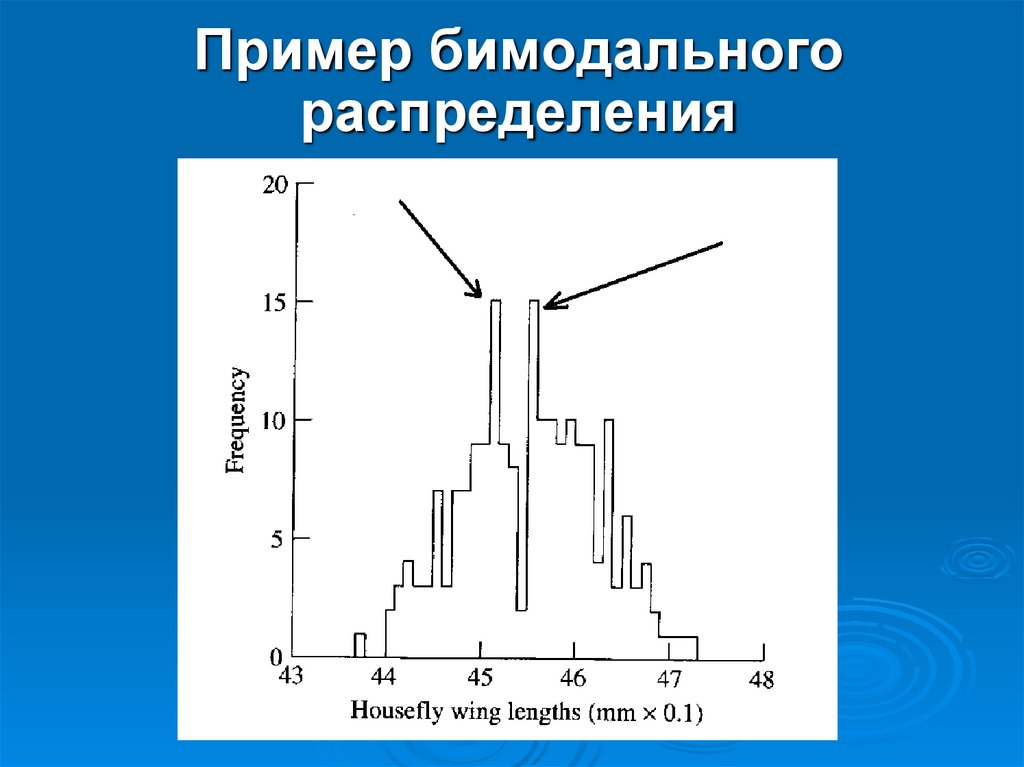
Характер вариации признака:
исследователь может установить,
какой класс является модальным.
(мода – наиболее часто встречающееся
значение)
11.
Пример бимодальногораспределения
12.
Вариационный ряд обычноизображают графически
Графическое изображение
вариационного ряда называется
кривой распределения или
вариационной кривой
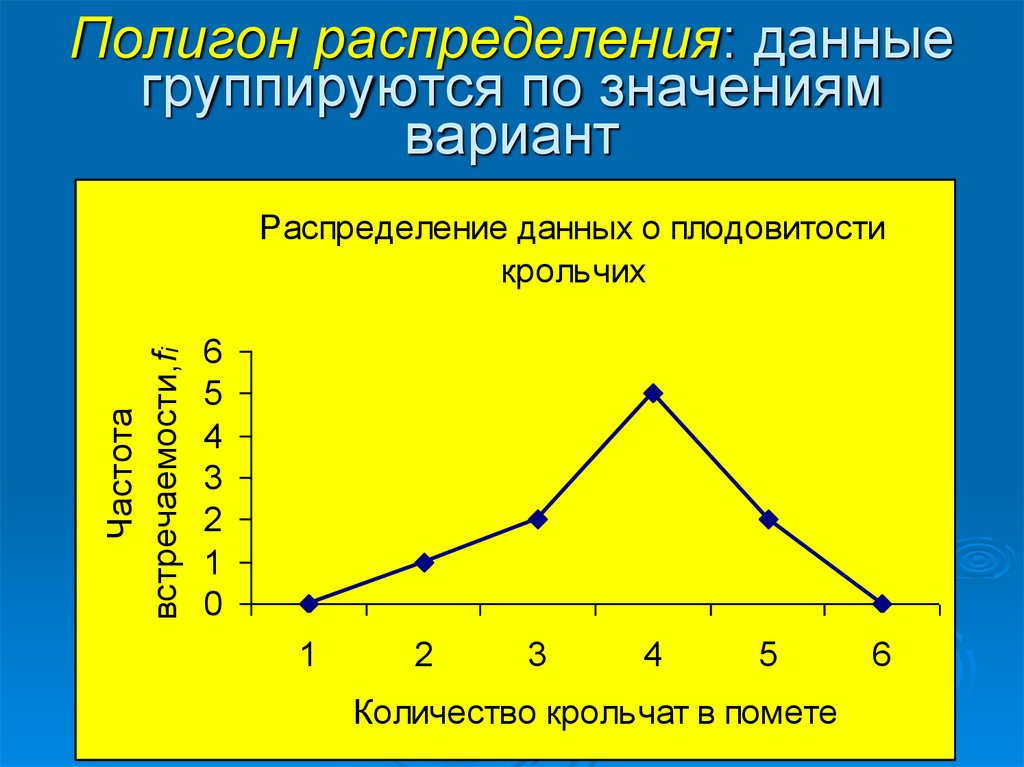
13. Полигон распределения: данные группируются по значениям вариант
Частотавстречаемости, fi
Распределение данных о плодовитости
крольчих
6
5
4
3
2
1
0
1
2
3
4
5
Количество крольчат в помете
6
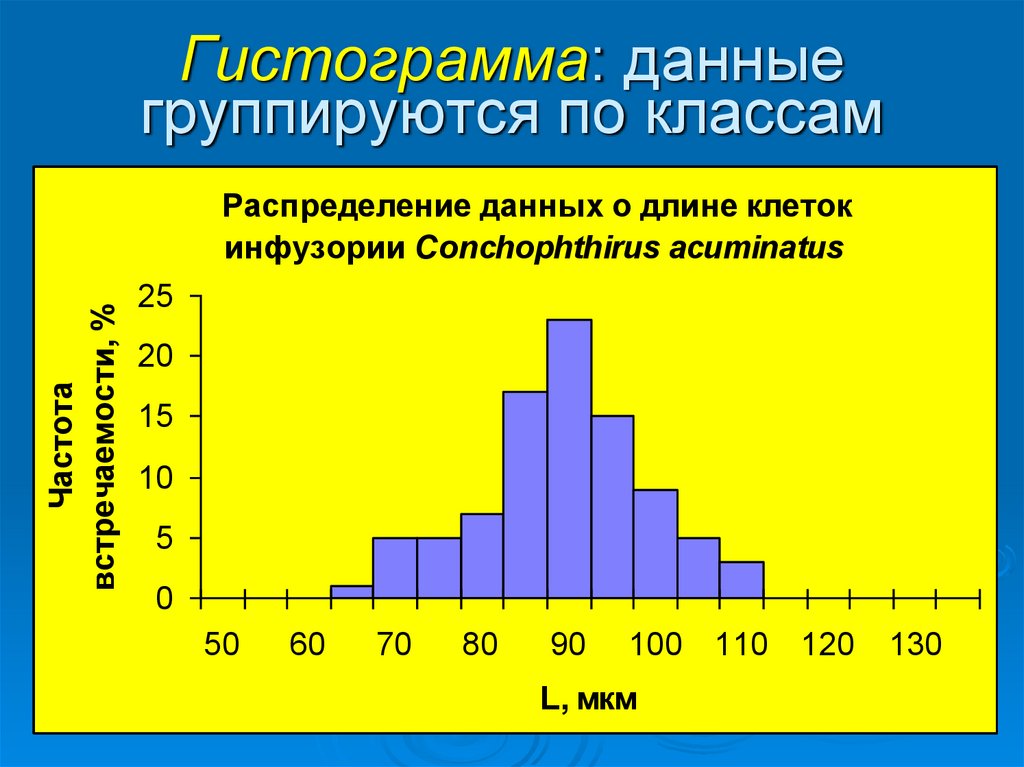
14. Гистограмма: данные группируются по классам
Частотавстречаемости, %
Распределение данных о длине клеток
инфузории Conchophthirus acuminatus
25
20
15
10
5
0
50
60
70
80
90
100
L, мкм
110
120
130
15.
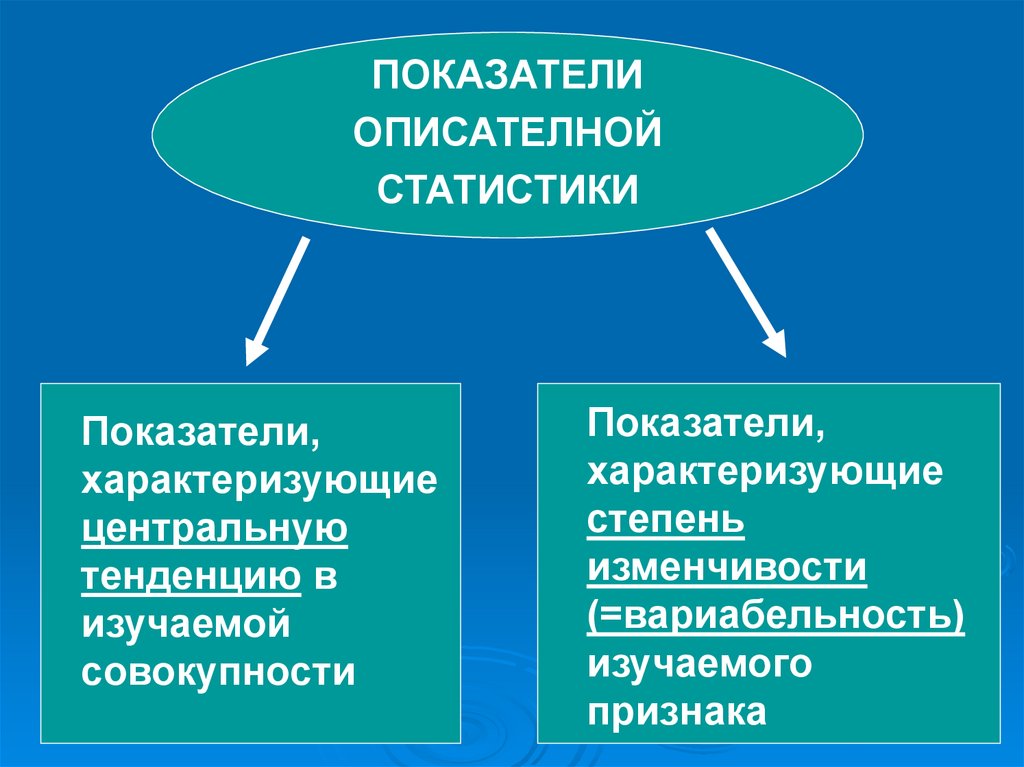
ПОКАЗАТЕЛИОПИСАТЕЛНОЙ
СТАТИСТИКИ
Показатели,
характеризующие
центральную
тенденцию в
изучаемой
совокупности
Показатели,
характеризующие
степень
изменчивости
(=вариабельность)
изучаемого
признака
16. 2.2. Среднее значение и стандартное отклонение
17. Многие лекционные примеры будут заимствованы из книги C. Гланца Пользуйтесь электронной версией книги (PDF)
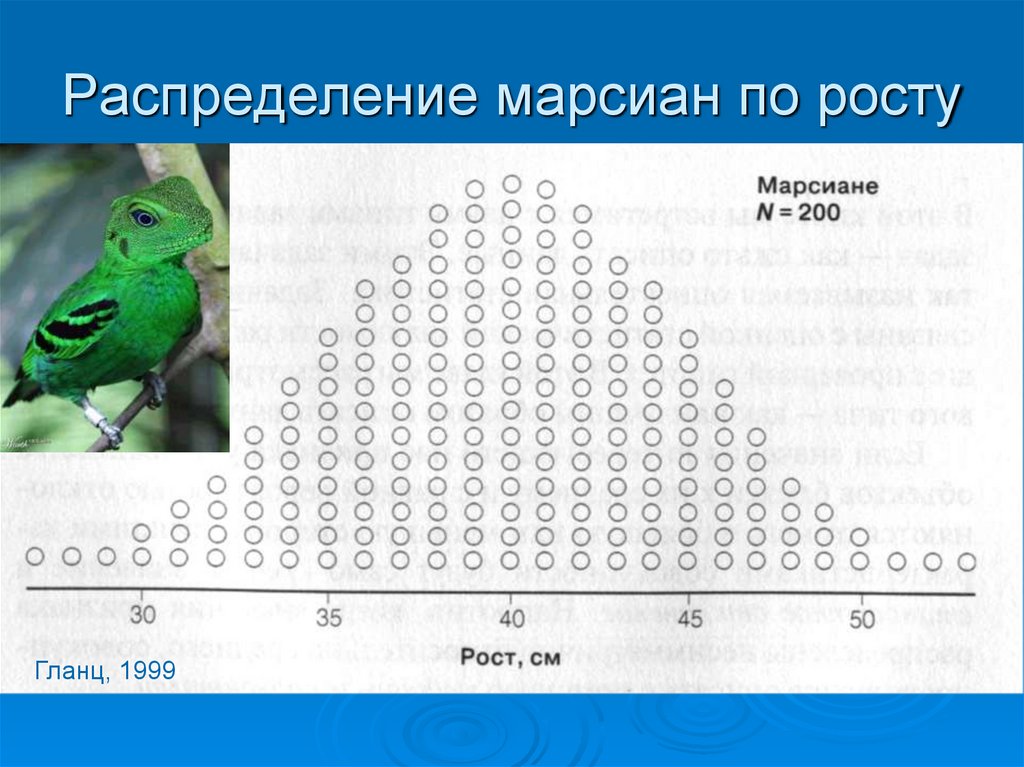
18. Распределение марсиан по росту
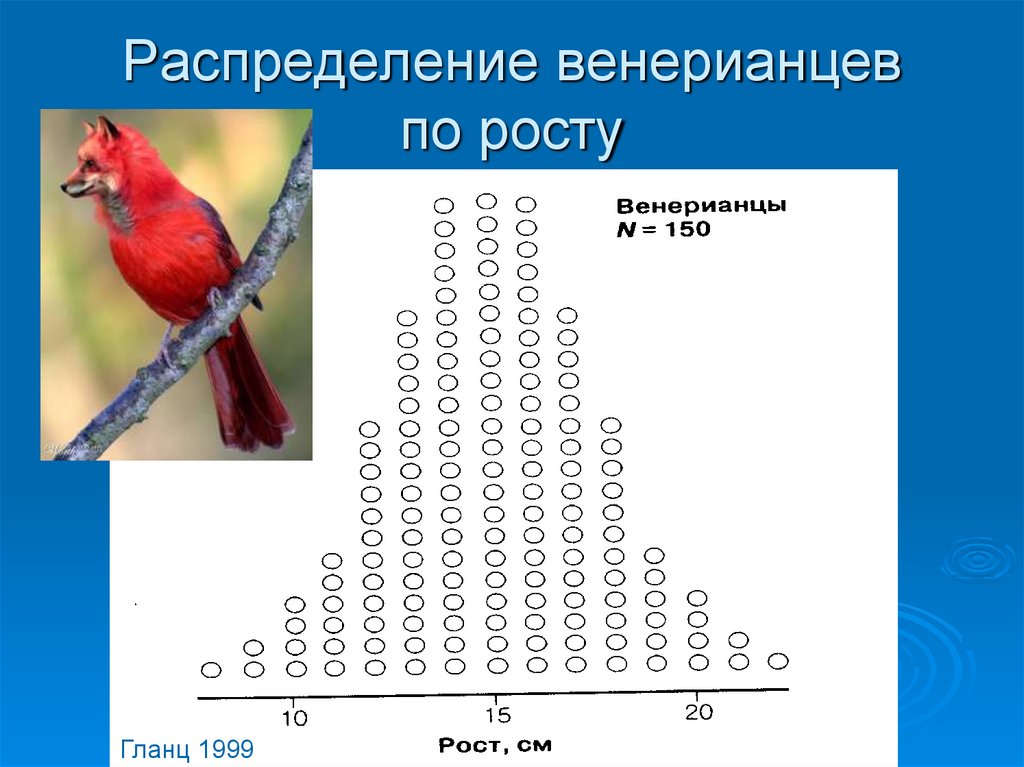
Гланц, 199919. Распределение венерианцев по росту
Гланц 199920. Сходства и различия распределений марсиан и венерианцев по росту
21.
Любое нормальное распределениеможно описать с помощью всего
двух параметров:
среднего значения (µ) и
стандартного отклонения (σ)
22. ВЫБОРОЧНАЯ СРЕДНЯЯ (англ.: sample mean) (= средняя арифметическая, среднее значение)
1x xi
n
23. ВЗВЕШЕННАЯ СРЕДНЯЯ (англ.: Weighted mean):
x1n1 x2 n2 ... xk nkx
nk
24. ГЕОМЕТРИЧЕСКАЯ СРЕДНЯЯ (англ.: Geometric mean):
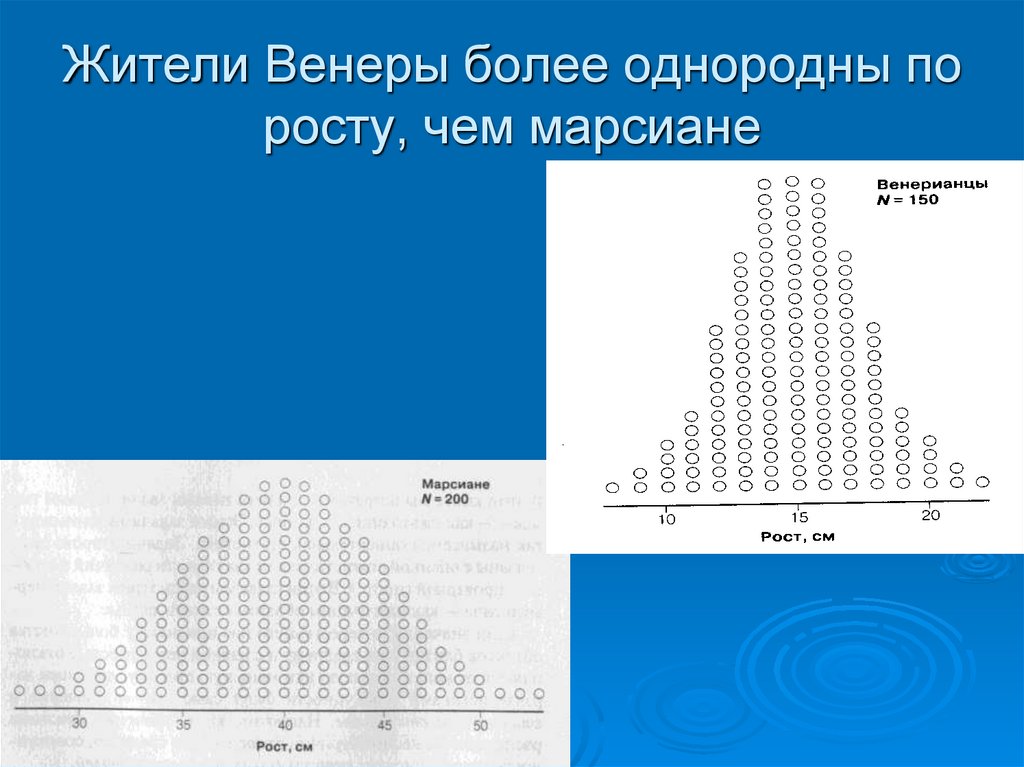
xg n x1 x2 ... xn25. Жители Венеры более однородны по росту, чем марсиане
26. Показатели вариабельности:
Размах (англ.: range) –разница между
максимальным и
минимальным значениями
вариант (лимитами).
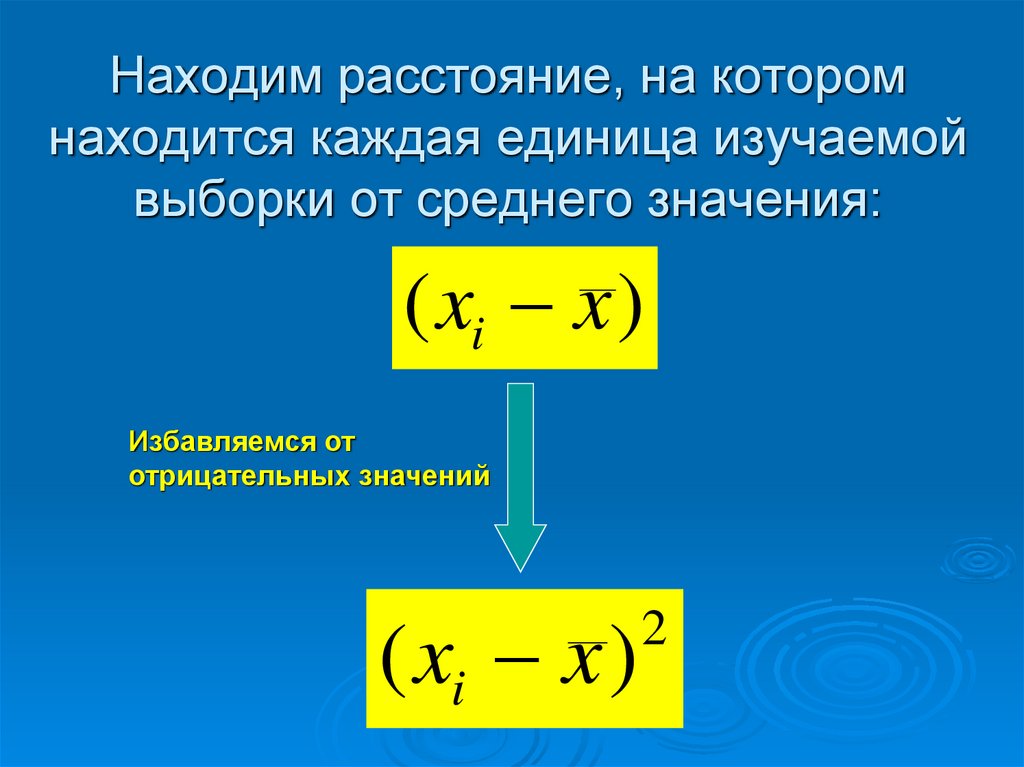
27. Находим расстояние, на котором находится каждая единица изучаемой выборки от среднего значения:
( xi x )Избавляемся от
отрицательных значений
( xi x )
2
28. Усредняем вычисленные расстояния и получаем дисперсию (англ.: variance):
SS (sum of squares) –сумма квадратов
(
x
x
)
i
2
s
n
2
29. Извлекая корень из дисперсии, получаем стандартное отклонение (англ.: standard deviation; SD):
(x
x
)
i
s
n
2
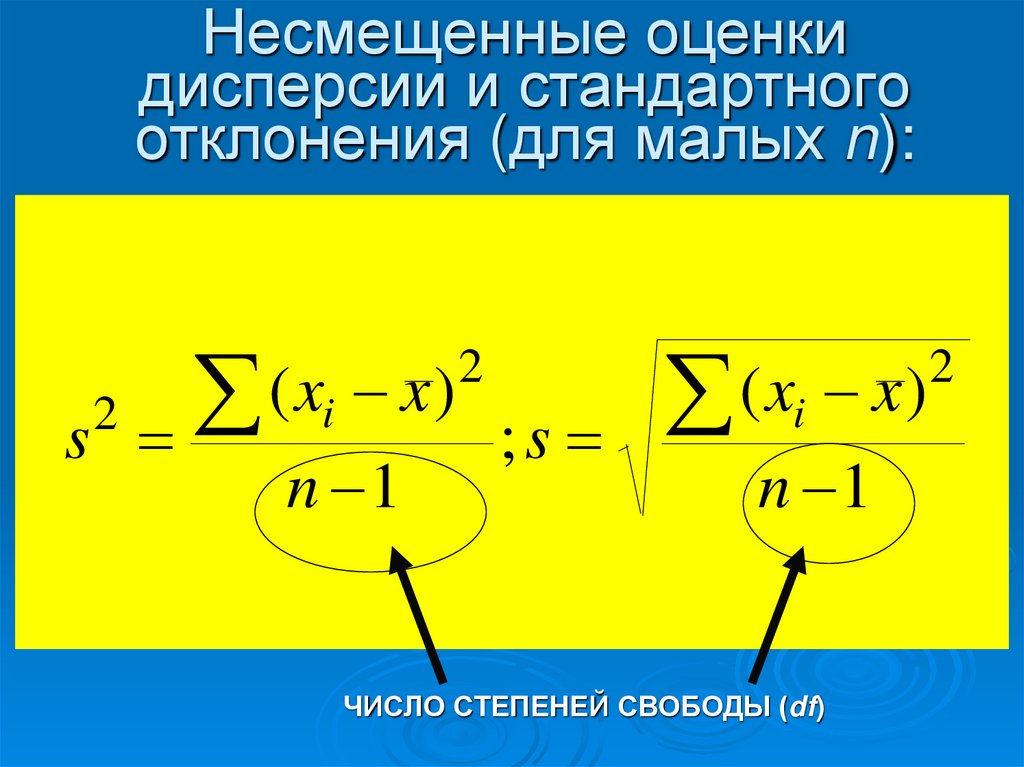
30. Несмещенные оценки дисперсии и стандартного отклонения (для малых n):
( xi x )( xi x )
s
;s
2
2
n 1
n 1
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ (df)
2
31. df = (n – 1): число степеней свободы (degree of freedom)
Допустим, A + B + C = 30Первые две варианты могут иметь
любые значения (например, 10 и 15)
НО (!): третья варианта может быть
равна только разнице между 30 и
суммой двух первых вариант (т.е. 5)
=> df = (n-1) = 2
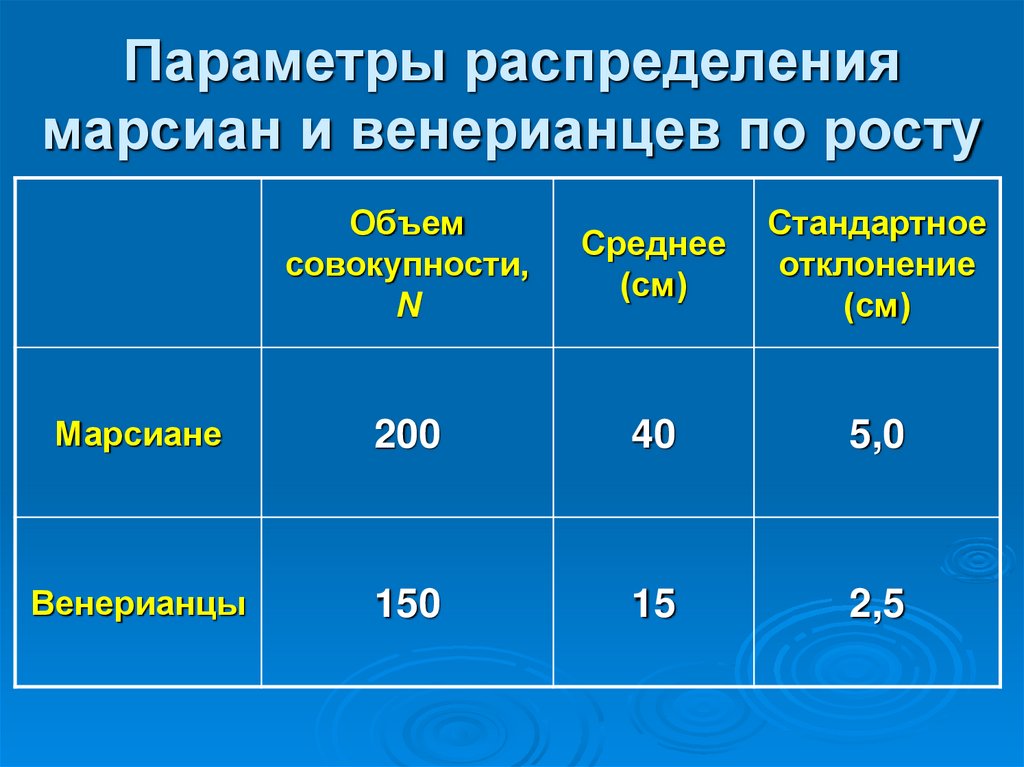
32. Параметры распределения марсиан и венерианцев по росту
Объемсовокупности,
N
Среднее
(см)
Стандартное
отклонение
(см)
Марсиане
200
40
5,0
Венерианцы
150
15
2,5
33. 2.3. Медиана и процентили
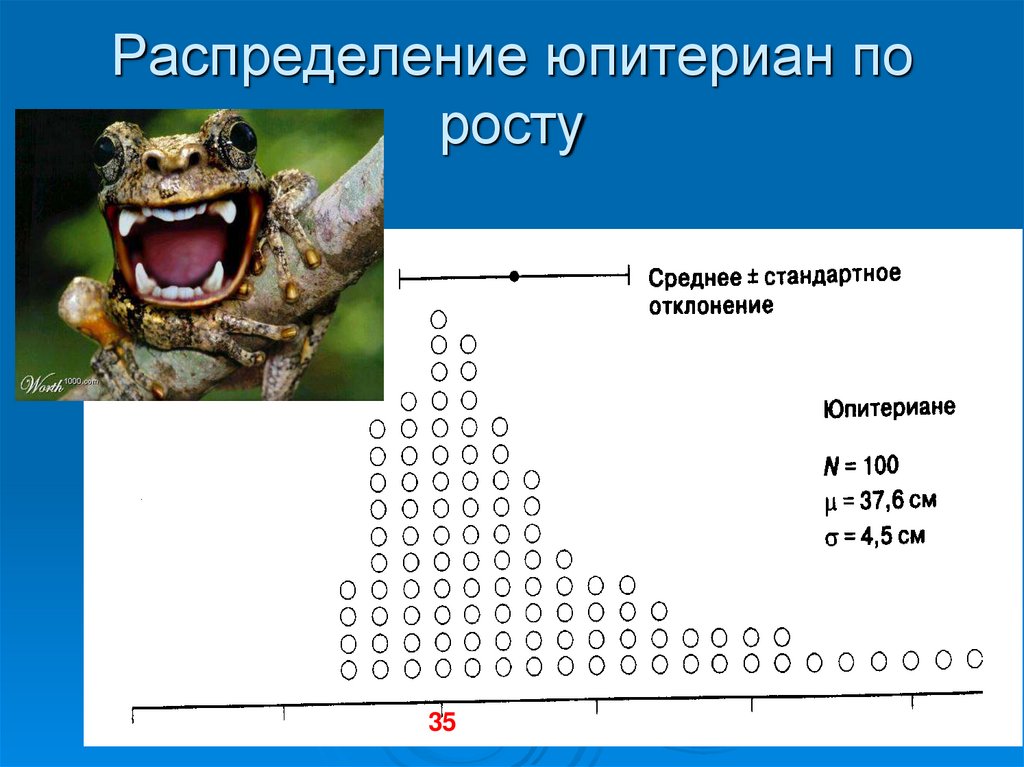
34. Распределение юпитериан по росту
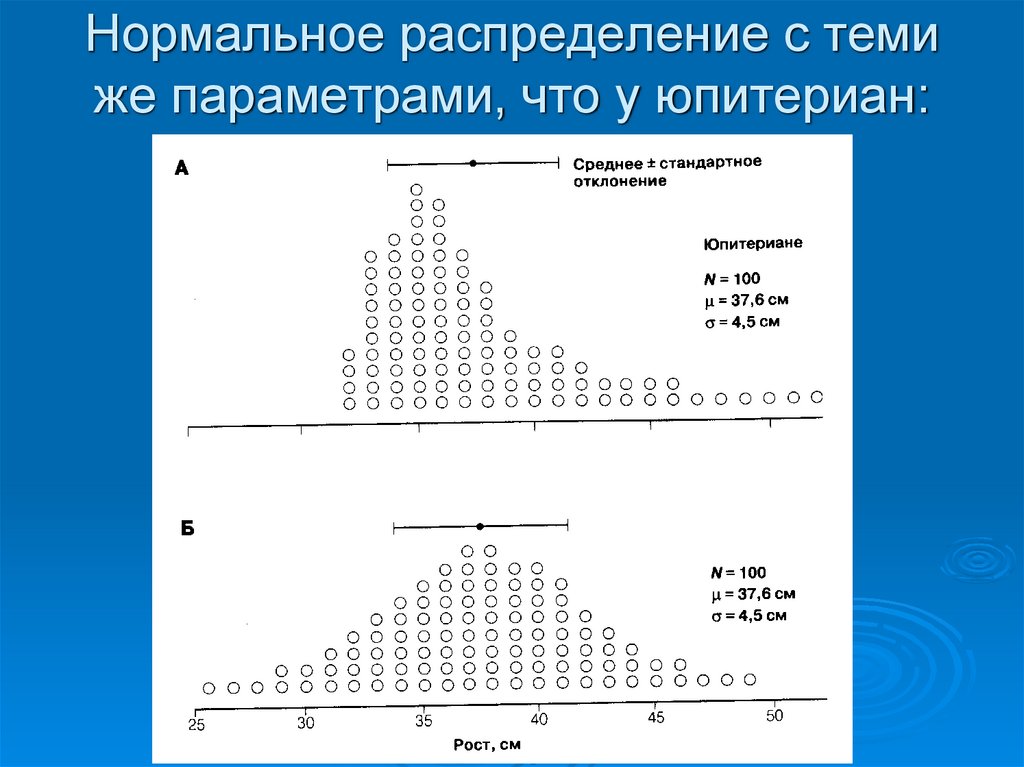
3535. Нормальное распределение с теми же параметрами, что у юпитериан:
36.
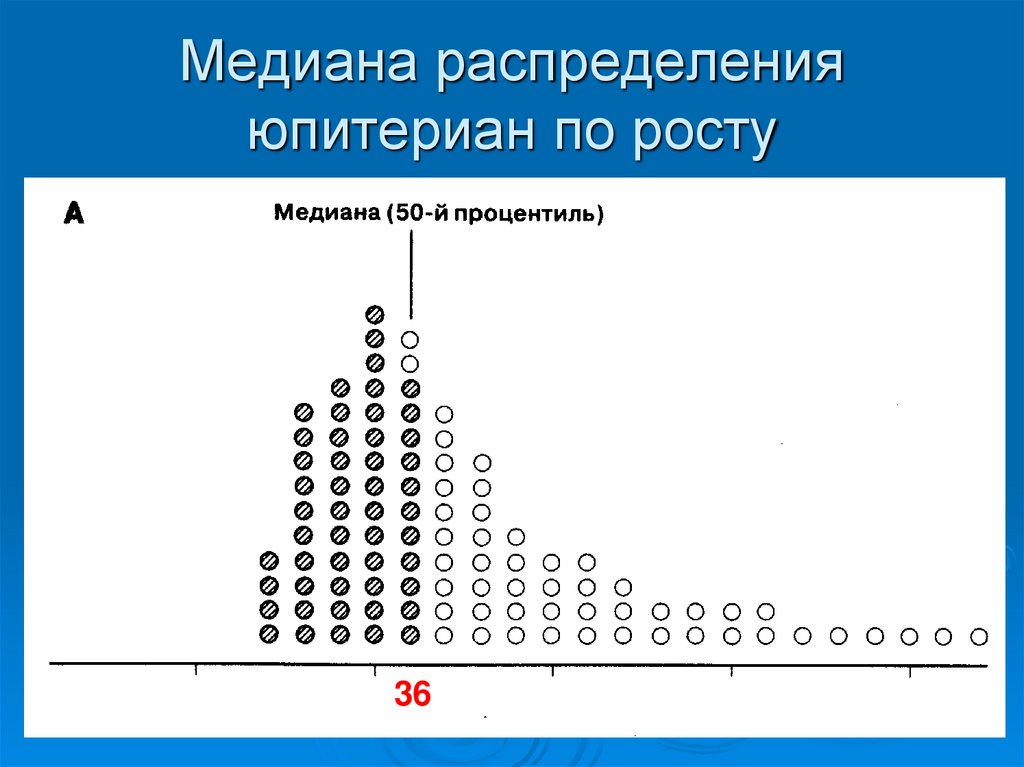
Медиана (Ме; англ.: Median) значение, которое делитраспределение ровно
пополам.
37. Медиана распределения юпитериан по росту
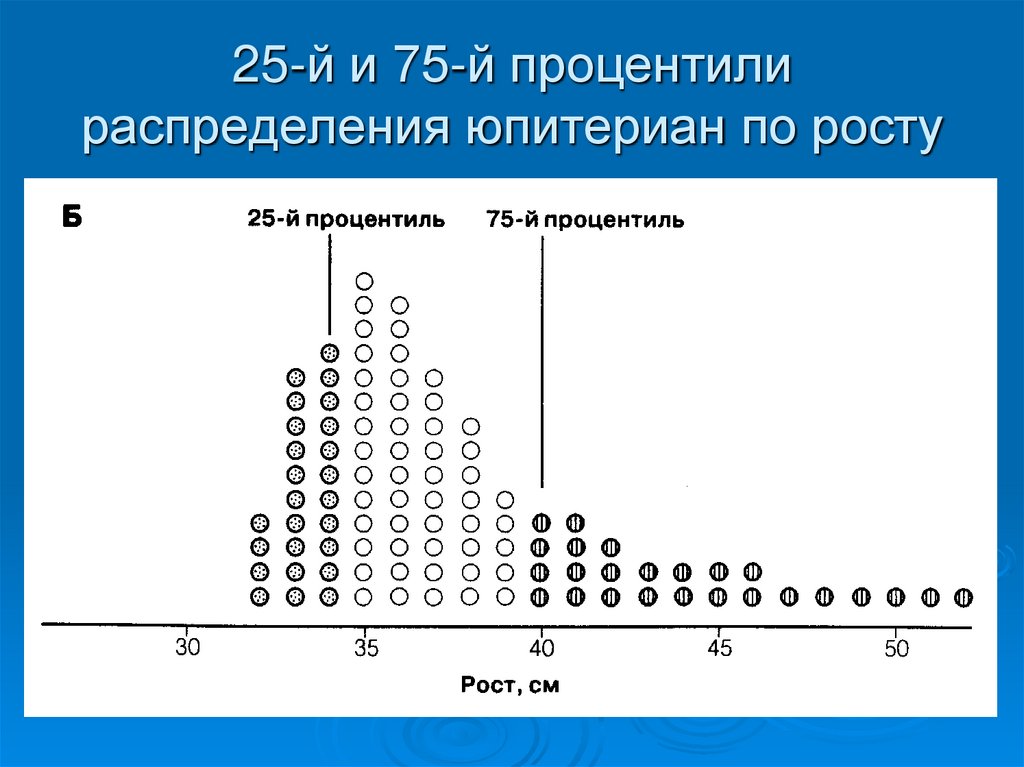
3638. 25-й и 75-й процентили распределения юпитериан по росту
39. ВЫВОДЫ:
Если известно, что выборка скореевсего принадлежит к совокупности
с нормальным распределением,
для ее описания лучше
использовать выборочное среднее
и выборочное стандартное
отклонение.
40. ВЫВОДЫ:
Если же известно, чтораспределение в совокупности
отличается от нормального,
следует использовать медиану,
25-й и 75-й процентили.
41.
DID YOU HEAR ABOUT THE STATISTICIAN WHO HAD HISHEAD IN AN OVEN AND HIS FEET IN A BUCKET OF ICE?
WHEN ASKED HOW HE FELT, HE REPLIED,
"ON THE AVERAGE I FEEL JUST FINE."
























 mathematics
mathematics








