Описательная статистика: продолжение. Лекция 3

1. ЛЕКЦИЯ 3

ОПИСАТЕЛЬНАЯ
СТАТИСТИКА:
ПРОДОЛЖЕНИЕ

2. 3.1. Показатели описательной статистики при качественной изменчивости

3. Распределение марсиан по окраске

150
50

4. Расчет доли марсиан, имеющих каждый из вариантов окраски:

Розовые особи: р = 50/200 = 0.25
Зеленые особи: q = 150/200 = 0.75
В общем случае:
p+q=1
или p% + q% = 100%

5.

Для характеристики совокупности
из двух классов достаточно указать
численность одного из них
р – вероятность того, что случайно
выбранный марсианин окажется
розовым

6. Доля р аналогична средней арифметической количественного признака:

xi 1 1 ... 1 0 0... 0
N
200
50 1 150 0 50
0.25
200
200

7. Что означает «разброс», если значений признака всего два???

8. Стандартное отклонение при качественной изменчивости:

s
pq
или (в абсолютных величинах):
s npq

9. Зависимость стандартного отклонения доли р от самой этой доли:

10.

3.2. Коэффициент
вариации

11. 3.2. Коэффициент вариации

«Что является более вариабельным:
рост марсиан (cм) или их вес (г)???»
Рост: 40±5 см
Вес: 20±1 г

12. «Что является более вариабельным: рост марсиан (cм) или их вес (г)???»

Коэффициент вариации:
s
CV 100%
x

13. «Что является более вариабельным: рост марсиан (cм) или их вес (г)???»

Для большинства
биологических исследований
величина СV не должна
превышать 20 %
Если СV больше 20 % мы имеем
дело с разнородной выборкой!

14.

3.3. Стандартная ошибка

15.

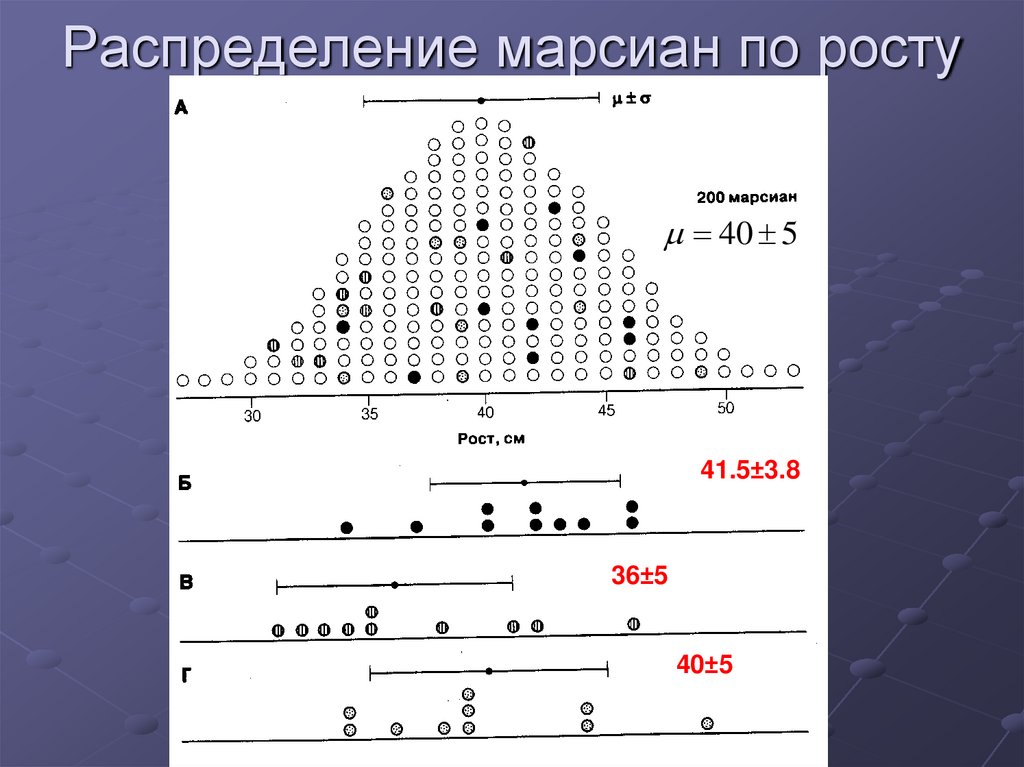
Распределение марсиан по росту
40 5
41.5±3.8
36±5
40±5

16. Распределение марсиан по росту

Распределение 25 средних
значений роста марсиан

17. Распределение 25 средних значений роста марсиан

Центральная предельная
теорема
Выборочные средние имеют
нормальное распределение
независимо от распределения
исходной совокупности и
объема выборок.

18. Центральная предельная теорема

Параметры распределения 25
средних значений роста марсиан
n 25
X x 40
S x 1.6

19. Параметры распределения 25 средних значений роста марсиан

Следствия центральной
предельной теоремы:
1) Средняя арифметическая,
полученная на основе нескольких
выборочных средних, совпадает
с генеральным средним
значением;

20. Следствия центральной предельной теоремы:

Параметры распределения 25
средних значений роста марсиан
n 25
X x 40
S x 1.6
σ = 5 см

21. Параметры распределения 25 средних значений роста марсиан

S x – стандартная ошибка
средней
Часто обозначается как SE
(от англ.: standard error)
мера точности, с которой
выборочное среднее оценивает μ

22. мера точности, с которой выборочное среднее оценивает μ

Следствия центральной
предельной теоремы:
2) Выборочные
средние варьируют
в √n раз меньше,
чем единицы
генеральной
совокупности:
Подставляя выборочное
стандартное отклонение,
получаем:
sx / n
s
sx
n

23. Следствия центральной предельной теоремы:

Стандартная ошибка =
ошибка репрезентативности:
Показывает, насколько близко
выборочная средняя находится по
отношению к генеральной средней.

24. Стандартная ошибка = ошибка репрезентативности:

Стандартная ошибка средней :
s
sx
n
По мере увеличения числа наблюдений
величина стандартной ошибки уменьшается.

25. Стандартная ошибка средней :

Закон Больших Чисел:
При неограниченном
возрастании числа
испытаний вероятность
наступления события А
будет максимально близка
к теоретически ожидаемой
вероятности его наступления.

26. Закон Больших Чисел:

3.4. Представление
средних величин, мер
разброса и стандартных
ошибок в научных
публикациях

27. 3.4. Представление средних величин, мер разброса и стандартных ошибок в научных публикациях

Структура научной публикации:
Введение (Introduction);
Материал и методы (Material and
Methods);
Результаты (Results);
Обсуждение (Discussion);
Благодарности (Acknowledgements);
Список литературы (Literature cited /
References).

28. Структура научной публикации:

В разделах «Материал и
методы» и/или «Результаты»
всегда необходимо приводить
объемы проанализированных
выборок (n)!

29.

Нужно стараться приводить
стандартное отклонение, т.к.
именно оно, а не стандартная
ошибка оценивает разброс
исходных данных!

30.

Пример, иллюстрирующий
необходимость приведения
стандартного отклонения
Измерен объем сердечного выброса у
200 человек (n = 200).
х = 5 л/мин
s = 1 л/мин
у 95% обследованных сердечный
индекс составил от 3 до 7 л/мин (х±2s).

31. Пример, иллюстрирующий необходимость приведения стандартного отклонения

Автор привел среднее значение и
стандартную ошибку: 5.0 ± 0.22 л/мин
спутав SE с SD, мы (читатели)
заключили бы, что у 95%
обследованных сердечный индекс
составлял от 5.44 до 4.56 л/мин.

32. Пример, иллюстрирующий необходимость приведения стандартного отклонения

В публикации всегда нужно
указывать, какой показатель
приводится вместе со
средним значением: стандартное
отклонение
или стандартная ошибка!

33.

Самый простой способ
графического представления
средней и SD (или SE)
«Усы»
(whiskers)

34. Самый простой способ графического представления средней и SD (или SE)

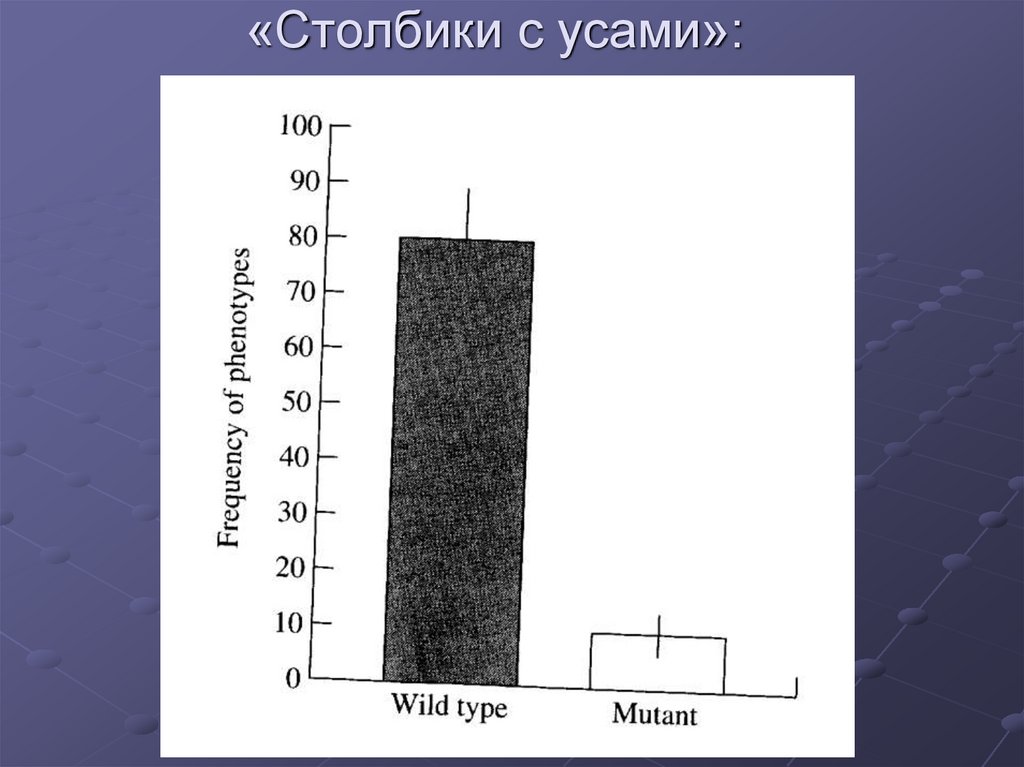
«Столбики с усами»:

35. «Столбики с усами»:

«Box-plots»:

36. «Box-plots»:

Знание некоторых
принципов легко
возмещает незнание
некоторых фактов
К. Гельвеций