Similar presentations:
Обратная матрица. Матричные уравнения
1.
«Обратная матрица. Матричные уравнения.»2.
1. Определение обратной матрицыКвадратная матрица называется невырожденной, если ее
определитель не равен нулю.
A 1 называется обратной по отношению к
матрице А, если A A 1 A 1 A E
Матрица
Теорема. Для невырожденной матрицы А существует
единственная обратная матрица A 1
3.
2. Способы нахождения обратной матрицы,
1)
С помощью алгебраических дополнений
Алгоритм нахождения обратной матрицы:
1)
Вычисление определителя матрицы А,
2)
Построение и транспонирование матрицы
A11
A
*Т
A 12
...
A1п
алгебраических дополнений
(союзная матрица)
3)
Нахождение обратной матрицы
А 1
1
A*Т
det A
A22
A22
...
A2 n
... Aп1
... Aп 2
... ...
... Ann
4.
Рассмотрим примеры.2 3
A
4 5
1. Найти матрицу, обратную данной
2 3
2 5 ( 3) 4 22
1) det A
4 5
2)
5 4
A
3 2
*
3) A*T 5 3
4 2
1 5 3
4) A 22 4 2
1
5. Нахождение обратной матрицы
2. Найти матрицу, обратную данной1) Находим определитель матрицы
2
4 5 18 0 1
3
4
1 2 1
1 1 4
4 5
2
A 3 1 2
4 1 1
0 3 1 ( 1)
1 1
3 2
18 1
(18 3 1) 55 0
1 3
2) Составляем союзную матрицу
3 2
1 2
3
2
A12 ( 1)
(3 8) 11
A11 ( 1)
1 2 3
4
1
1 1
Т.о. обратная матрица существует.
A13 ( 1) 4
3 1
3 4 1
4 1
2 4
2 5
4 5
5
4
(2 16) 18
2 20 22 A23 ( 1)
A21 ( 1)
(4 5) 1 A22 ( 1)
4
1
4
1
1 1
3
A31 ( 1) 4
4 5
2 5
2 4
8 5 13 A32 ( 1)5
(4 15) 11 A33 ( 1) 6
2 12 14
1 2
3 2
3 1
3 11 1
*
A 1 22 18
13 11 14
3) Полученную матрицу транспонируем 4) Обратная матрица
1
13
1
13
3
3
1
A*T 11 22
11
A 1 11 22 11
55
1 18 14
1 18 14
6.
2) С помощью элементарных преобразований (Метод Гаусса)Алгоритм нахождения обратной матрицы :
1)
К матрице А справа приписывается Е,
2)
Проделывая преобразования над строками расширенной
матрицей (А|Е), матрицу А приводят к Е,
3)
Справа на месте приписанной матрицы Е будет
получена обратная матрица.
7. Элементарные преобразования матриц
• 1 строки матрицы можно менятьместами
• 2 строку можно умножать на любое
число, не равное нулю
• 3 к элементам любой строки можно
прибавлять соответствующие
элементы другой строки,
умноженные на одно и то же число
8.
9.
10.
11.
12.
13. Матричные уравнения
Матричные уравнения – это уравнения, в которых участвуюткак известные матрицы, так и неизвестная матрица, которую
и нужно найти. Существуют два основных типа матричных уравнений.
1 тип (левое умножение)
A X B
A 1 A X A 1 B
E X A 1 B
X A 1 B
2 тип (правое умножение)
X A B
X A A 1 B A 1
X E B A 1
X B A 1
В виде матричного уравнения A X B может быть
записана система линейных уравнений, решение которой
существует, если определитель основной
X A 1 B
матрицы отличен от нуля.
14.
2 54 6
Х
1 3
2 1
detA=
2 5
=1≠0, следовательно, А – невырожденная матрица.
1 3
Находим А-1:
А11=(-1)1+1∙3=3,
3
А12=(-1)1+2∙1=-1, А21=(-1)2+1∙5= -5, А22=(-1)2+2∙2=2, А*=
.
А-1=
1 3 5 3 5
1 1 2 1 2
5
1 2
Так как дано матричное уравнение первого типа, то Х=А-1∙В=
3 5 4 6 3 4 ( 5) 2 3 ( 6) ( 5) ( 1) 2 13
4
1 2 2 1 1 4 2 2 1 ( 6) 2 ( 1) 0
15. Матричный метод решения систем линейных уравнений
16.
Если в системе количество уравнений и неизвестных разное,то нельзя говорить об определителе основной матрицы и решать
систему матричным методом нельзя.









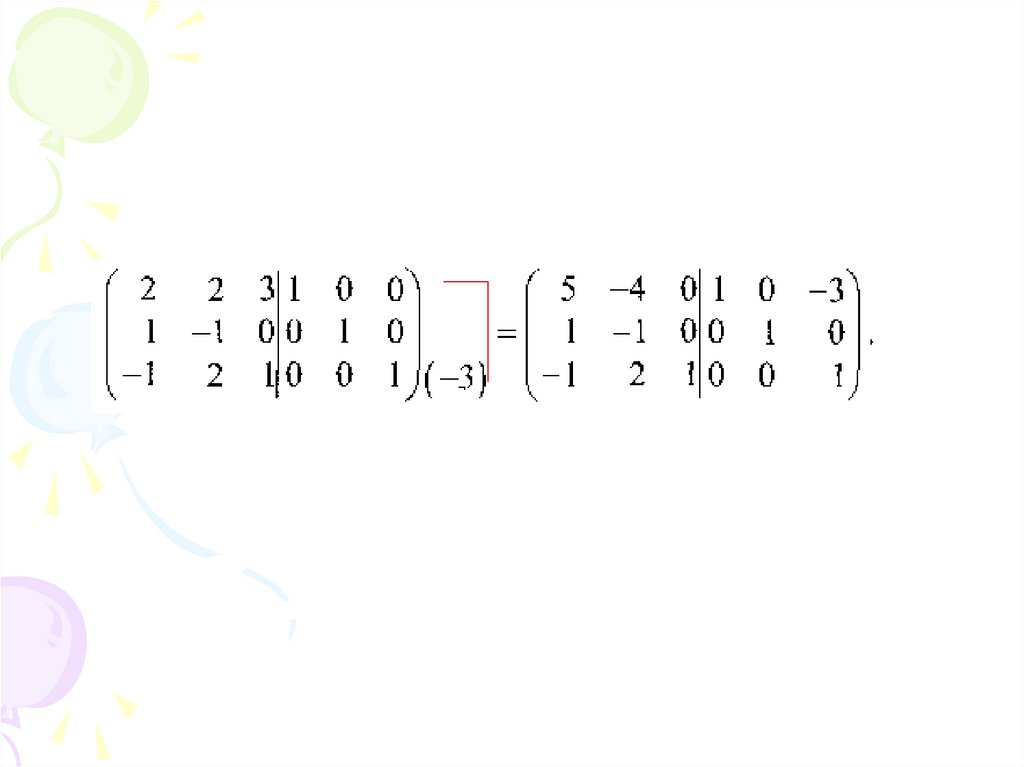






 mathematics
mathematics








