Similar presentations:
Домашнее задание по курсу «Детали машин» №4: «Проверочный расчет тихоходного вала редуктора»
1. Домашнее задание по курсу «Детали машин» №4
«Проверочный расчеттихоходного вала редуктора»
2. 1. Расчет силовых нагрузок на вал и построение эпюр изгибающих моментов и крутящего момента:
1.1. Расчет силовых нагрузок:1.1.1. Расчетная схема вала редуктора:
Fr
RA
Fa
Ft
A
Х
C
l1
d2
RB
FM
B
D
T2
l2
l3
3. 1.1.2. Тангенциальная сила, н:
Ft2 T 2 2 1000 T 2
d2
d2
1.1.3. Радиальная сила, н:
Fr
Ft tg
cos
20 o - угол зацепления; tg 0 , 364
угол наклона зубьев.
соs = соs0 = 1 для прямозубой передачи.
4. 1.1.4. Осевая сила, н:
Fa Ft tgtgβ = tg0 = 0, поэтому при прямозубом зацеплении осевая сила отсутствует.
1.1.5. Сила реакции в муфте, н:
F м 0 , 3 Ft
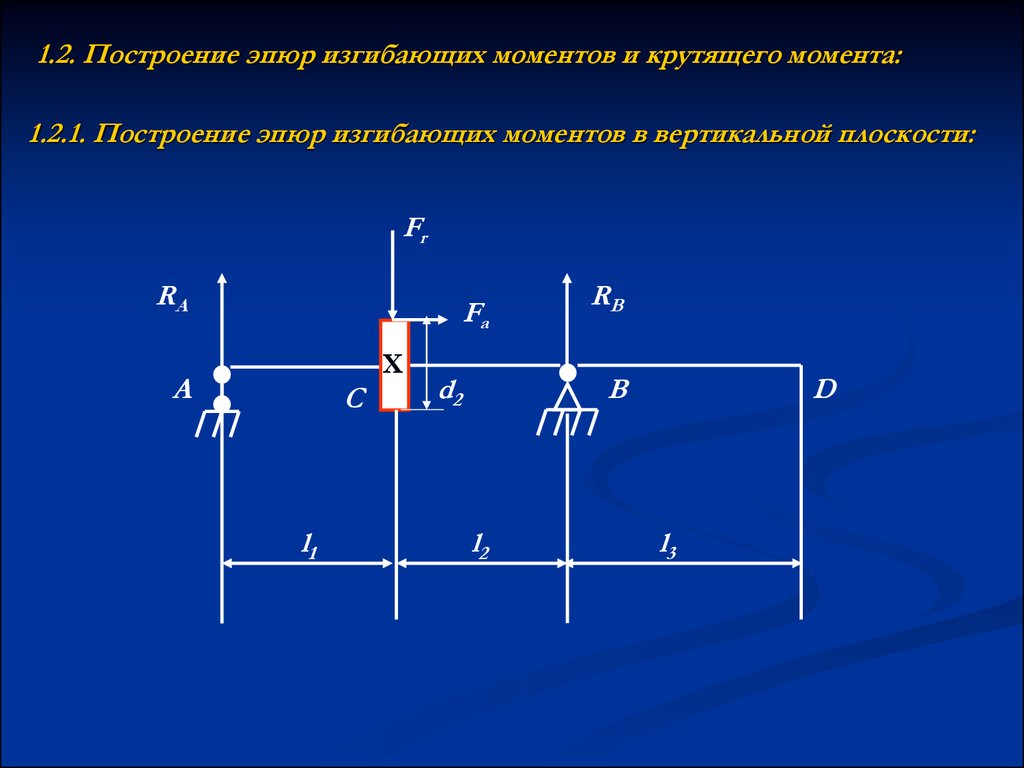
5. 1.2. Построение эпюр изгибающих моментов и крутящего момента:
1.2.1. Построение эпюр изгибающих моментов в вертикальной плоскости:Fr
RA
Fa
Х
A
C
l1
d2
RB
B
l2
D
l3
6. Определение опорных реакций от радиальной Fr и осевой Fa сил:
MB 0;d2
0;
Ray ( l 1 l 2 ) F r l 2 Fa
2
d
F r l 2 Fa 2
2 ,н;
Ray
( l1 l2 )
MA 0;
d2
0;
Rby ( l 1 l 2 ) F r l 1 Fa
2
d
F r l 1 Fa 2
2 , н.
Rby
( l1 l2 )
Проверяем правильность определения реакций:
R y 0 ; Ray Fr Rby 0
7. Если реакции найдены правильно, строим эпюру изгибающих моментов от сил радиальной и осевой:
М иy Ray l 1 , н мFr
RA
Fa
Х
A
C
l1
Миy
d2
RB
B
l2
D
l3
8. 1.2.2. Построение эпюр изгибающих моментов в горизонтальной плоскости:
FtRA
RB
Х
A
C
l1
d2
B
l2
D
l3
9. Определение опорных реакций от тангенциальной силы Ft:
MB 0;Rax l 1 l 2 Ft l 2 0 ;
F l
Rax t 2 , н ;
l 1 l 2
MA 0;
Rbx l 1 l 2 Ft l 1 0 ;
Ft l 1
,н;
Rbx
l 1 l 2
Rax Rbx
Проверяем правильность определения реакций:
R x 0 ; Rax Ft Rbx 0
10. Если реакции найдены правильно, строим эпюру изгибающих моментов от тангенциальной силы:
М их Raх l 1 , н мFt
RA
RB
Х
A
C
l1
Мих
d2
B
l2
D
l3
11. 1.2.3. Построение суммарной эпюры изгибающего момента от действия тангенциальной, радиальной и осевой сил:
22
M И M их
M иу
,н м
Fr
Fa
Ft
A
C
l1
МИ
Х
d2
B
l2
D
l3
12. 1.2.4. Построение эпюры изгибающих моментов от действия силы FМ:
На консольном участке вала находится полумуфта, которая нагружаетвал дополнительно поперечной силой .
RA
FМ
RB
Х
A
B
C
l1
l2
D
l3
13. Определение опорных реакций от действия силы FМ :
MA 0;RbM l 1 l 2 F M ( l 1 l 2 l 3 ) 0 ;
F ( l 1 l 2 l 3 )
RbМ M
,н;
l 1 l 2
Меняем направление реакции в точке В
MB 0;
RaM l 1 l 2 F M l 3 0 ;
F l
RaМ M 3 , н ;
l 1 l 2
Проверяем правильность определения реакций:
R М 0 , RaM RbM F M 0
14. Если реакции найдены правильно, строим эпюру изгибающих моментов от действия силы реакции в муфте:
M ИM RaM ( l 1 l 2 ), н мRA
RB
Х
A
B
C
l1
МИМ
FМ
l2
D
l3
15. 1.2.5. Построение суммарной эпюры изгибающих моментов от действия всех сил:
M И M И М ИМ , н мFr
RA
Fa
Ft
A
C
l1
МИ
Х
d2
RB
FM
B
l2
D
l3
16. 1.2.6. Построение эпюры крутящего момента:
ХA
B
C
l1
T2
l2
Т2
D
l3
17.
Сводная эпюра изгибающих и крутящих моментов18. 2. Уточненный расчет тихоходного вала редуктора
Уточненный расчет выполняют, как проверочный для определениярасчетного коэффициента запаса прочности:
SП
S S
S 2 S 2
Коэффициент запаса прочности по нормальным напряжениям:
S
1
k a
ср .
Коэффициент запаса прочности по касательным напряжениям:
S
1
k a
ср .
19.
Пределы выносливости материала вала при симметричных циклах изгибаи кручения, если нет табличных данных, тогда для углеродистых сталей:
1 0 ,43 B , МПа
1 0 ,58 1 , МПa
Расчетный коэффициент запаса прочности определяют в опасном
сечении. Опасным считается сечение вала, для которого коэффициент
запаса прочности имеет наименьшее значение, оно может не совпадать с
сечением, где возникают наибольший изгибающий и крутящий моменты,
поэтому следует проверять все опасные сечения.
S П 1 ,5 4
20. Опасные сечения в точках С и Е
21. 2.1. Проверка прочности сечения в точке С:
Дано:dз.к.= …
МиС= …
Т2 = …
b=…
t1 = …
В=520МПа,
т =280МПа,
τТ =170МПа,
-1 =250МПа,
τ-1 =150МПа
22. Напряжения изгиба изменяются по симметричному циклу, напряжения кручения – по отнулевому (пульсирующему) циклу:
а Иср . 0
а ср .
MИ
W И .НЕТТО
, МПа ;
К
Т2
, МПа.
2
2 W K .НЕТТО
23. 2.1.1. Моменты сопротивления валов при изгибе Wи.нетто и кручении Wк.нетто в сечении ослабленном шпоночным пазом определяются:
W и .неттоd з3.к b t 1 d з .к t 1 2
, мм 3
32
2 d з .к
W к .нетто
d з3.к b t 1 d з .к t 1 2
, мм 3
16
2 d з .к
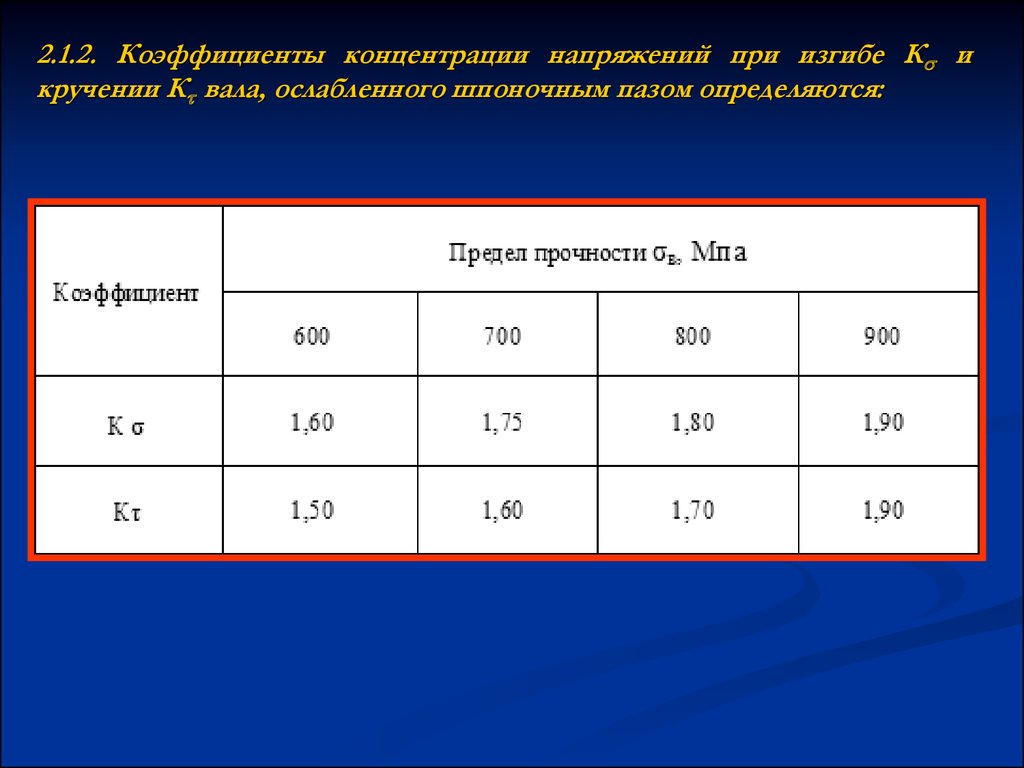
24. 2.1.2. Коэффициенты концентрации напряжений при изгибе К и кручении К вала, ослабленного шпоночным пазом определяются:
2.1.2. Коэффициенты концентрации напряжений при изгибе К икручении К вала, ослабленного шпоночным пазом определяются:
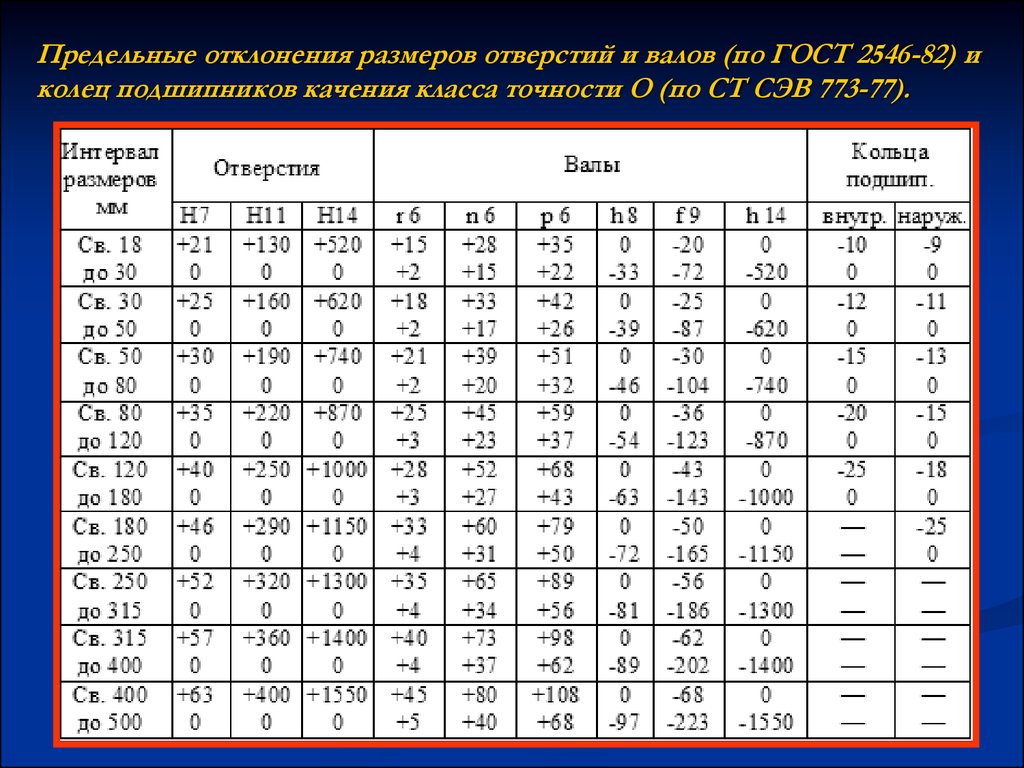
25. 2.1.3. Масштабные факторы при изгибе и кручении для углеродистых сталей определяются из таблицы, в соответствии с пределом прочности
2.1.3. Масштабные факторы при изгибе и кручении дляуглеродистых сталей определяются из таблицы, в соответствии с
пределом прочности и диаметром вала в данном сечении.
26. 2.1.4. Коэффициент β, зависящий от степени шероховатости поверхности (способ обработки) определяется по таблице, для качественных поверхност
2.1.4. Коэффициент β, зависящий от степени шероховатостиповерхности (способ обработки) определяется по таблице, для
качественных поверхностей способ обработки шлифование:
27. 2.1.5. Коэффициенты, зависящие от соотношения пределов выносливости при симметричном и пульсирующем циклах напряжений ψ и ψ , выбирают в с
2.1.5. Коэффициенты, зависящие от соотношения пределоввыносливости при симметричном и пульсирующем циклах напряжений
ψ и ψ , выбирают в соответствии с маркой материала:
0 ,15 - углеродистая сталь σв = 350…550 МПа,
0 , 2 - углеродистая сталь σв = 650…750 МПа,
0 , 25...0 , 3 - легированная сталь,
0 ,05 - углеродистая сталь,
0 ,1 - легированная сталь,
Подставляем значения в формулы, расчетное значение коэффициента
запаса прочности сравниваем с допускаемым , если условие выполняется,
тогда прочность вала в данном сечении обеспечена.
28. 2.2. Проверка прочности сечения в точке Е:
Дано:dп= …
r=
МиЕ= …
Т2 = …
В=520МПа,
т =280МПа,
τТ =170МПа,
-1 =250МПа,
τ-1 =150МПа
r 0 ,4 d з .к . d п
A
МИ
Х
C
B
lст.
МиЕ
l2
D
29. Напряжения изгиба изменяются по симметричному циклу, напряжения кручения – по отнулевому (пульсирующему) циклу:
а Иср . 0
а ср .
MИ
W И .НЕТТО
, МПа ;
К
Т2
, МПа.
2
2 W K .НЕТТО
30. 2.2.1. Моменты сопротивления валов при изгибе Wи.нетто и кручении Wк.нетто для сплошного круглого сечения определяются :
W и .неттоd з3.к
, мм 3
32
W к .нетто
d з3.к
, мм 3
16
31. 2.2.2. Коэффициенты концентрации напряжений при изгибе К и кручении К вала, с галтелью определяются:
2.2.2. Коэффициенты концентрации напряжений при изгибе К икручении К вала, с галтелью определяются:
32. 2.2.3. Масштабные факторы при изгибе и кручении для углеродистых сталей определяются из таблицы, в соответствии с пределом прочности
2.2.3. Масштабные факторы при изгибе и кручении дляуглеродистых сталей определяются из таблицы, в соответствии с
пределом прочности и диаметром вала в данном сечении.
33. 2.2.4. Коэффициент β, зависящий от степени шероховатости поверхности (способ обработки) определяется по таблице, для качественных поверхност
2.2.4. Коэффициент β, зависящий от степени шероховатостиповерхности (способ обработки) определяется по таблице, для
качественных поверхностей способ обработки шлифование:
34. 2.2.5. Коэффициенты, зависящие от соотношения пределов выносливости при симметричном и пульсирующем циклах напряжений ψ и ψ , выбирают в с
2.2.5. Коэффициенты, зависящие от соотношения пределоввыносливости при симметричном и пульсирующем циклах напряжений
ψ и ψ , выбирают в соответствии с маркой материала:
0 ,15 - углеродистая сталь σв = 350…550 МПа,
0 , 2 - углеродистая сталь σв = 650…750 МПа,
0 , 25...0 , 3 - легированная сталь,
0 ,05 - углеродистая сталь,
0 ,1 - легированная сталь,
Подставляем значения в формулы, расчетное значение коэффициента
запаса прочности сравниваем с допускаемым , если условие выполняется,
тогда прочность вала в данном сечении обеспечена.
































 mechanics
mechanics








