Повторення та розширення відомостей про функцію

1. Повторення та розширення відомостей про функцію

* Повторення та
розширення
відомостей про
функцію

2.

Функція – одне з найважливіших понять
сучасної математики.
Воно було введено у XVII столітті,
коли у зв'язку з розвитком механіки
у математику проникли ідеї зміни і руху.

3.

Французькі математики П'єр Ферма (1601-1665)
та Рене Декарт (1596-1650) розглядали
функцію як залежність ординати точки кривої
від її абсциси.

4.

Термін «функція» (від
латинського functio —
виконання, звершення)
для назви залежностей
вперше ввів Готфрід
Лейбніц (1646-1716).
Він пов'язував функцію з
графіками.

5.

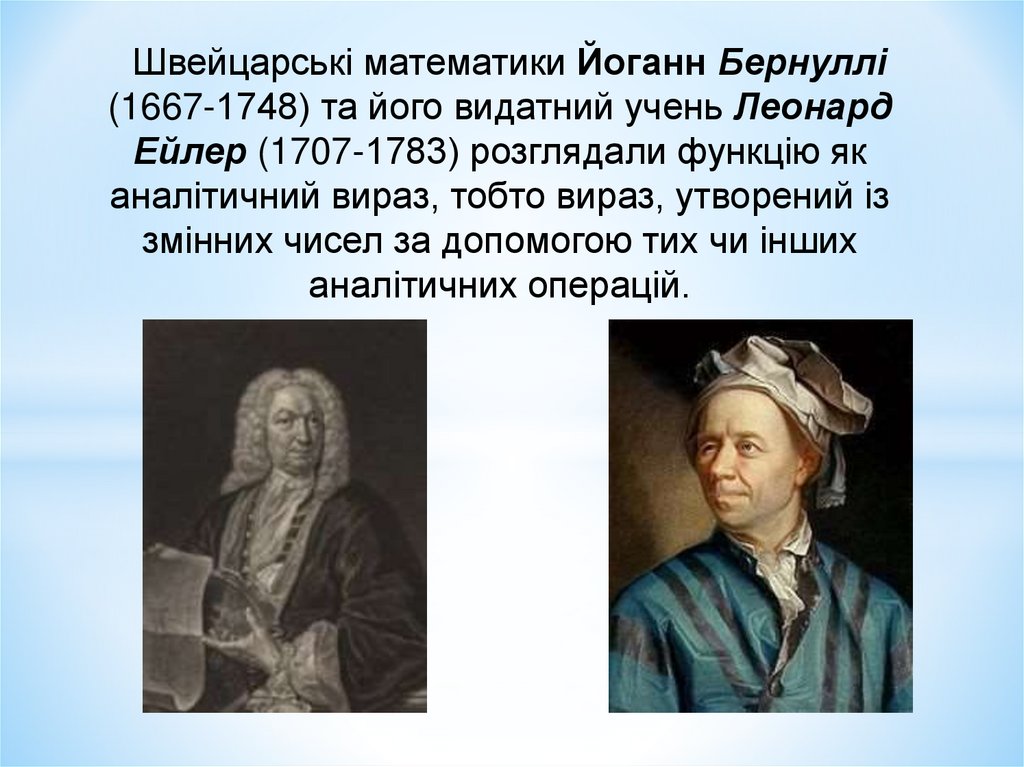
Швейцарські математики Йоганн Бернуллі
(1667-1748) та його видатний учень Леонард
Ейлер (1707-1783) розглядали функцію як
аналітичний вираз, тобто вираз, утворений із
змінних чисел за допомогою тих чи інших
аналітичних операцій.

6.

Функцію як залежність
однієї змінної величини від
іншої ввів чеський
математик Бернард
Больцано (1781-1848).
Найзагальніше сучасне означення поняття
«функція» запропонувала в середині
XX ст. група математиків, яка виступила під
псевдонімом Нікола Бурбакі.

7. Фронтальна бесіда

*
1. Сформулюйте означення функції.
2. Що називають незалежною змінною
(аргументом) функції?
3. Які є способи задання функції?
4. Що таке графік функції?
5. Що називають областю визначення
функції?
6. Що називають областю значення
функції?

8.

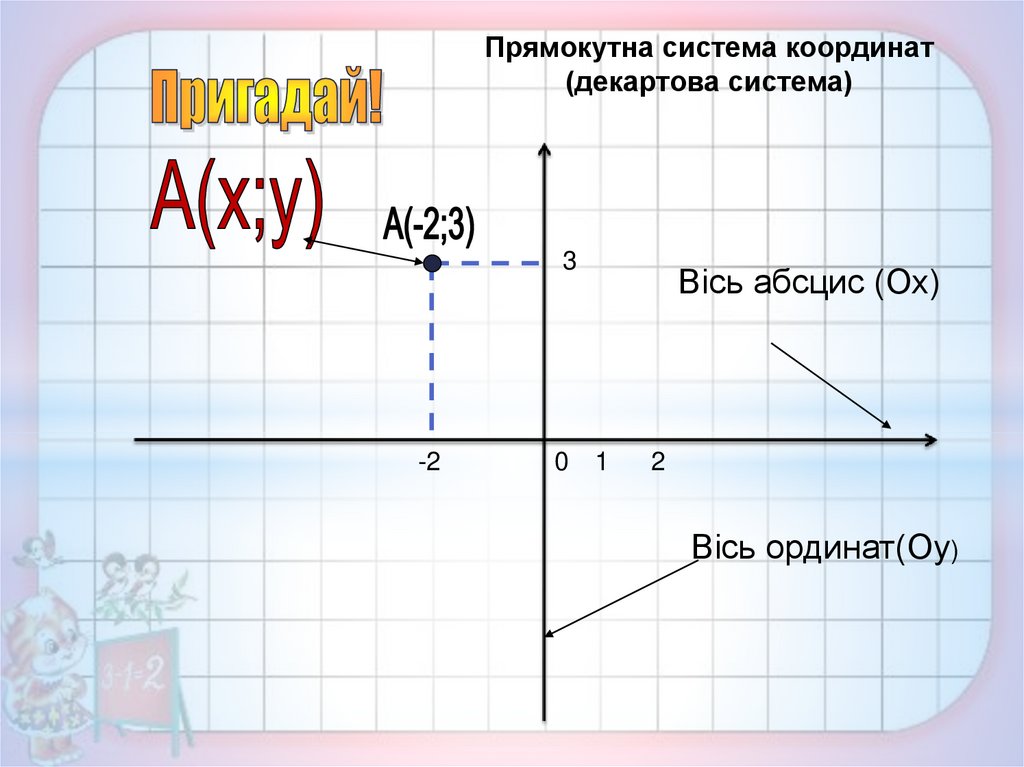
Прямокутна система координат
(декартова система)
3
-2
0
Вісь абсцис (Ох)
1
2
Вісь ординат(Оу)

9. Функцією називається залежність між х та єдиним у

* Функцією
залежність
у
х
Х
незалежна
у
залежна
змінна;
змінна;
абсциса;
ордината;
аргумент
функція

10.

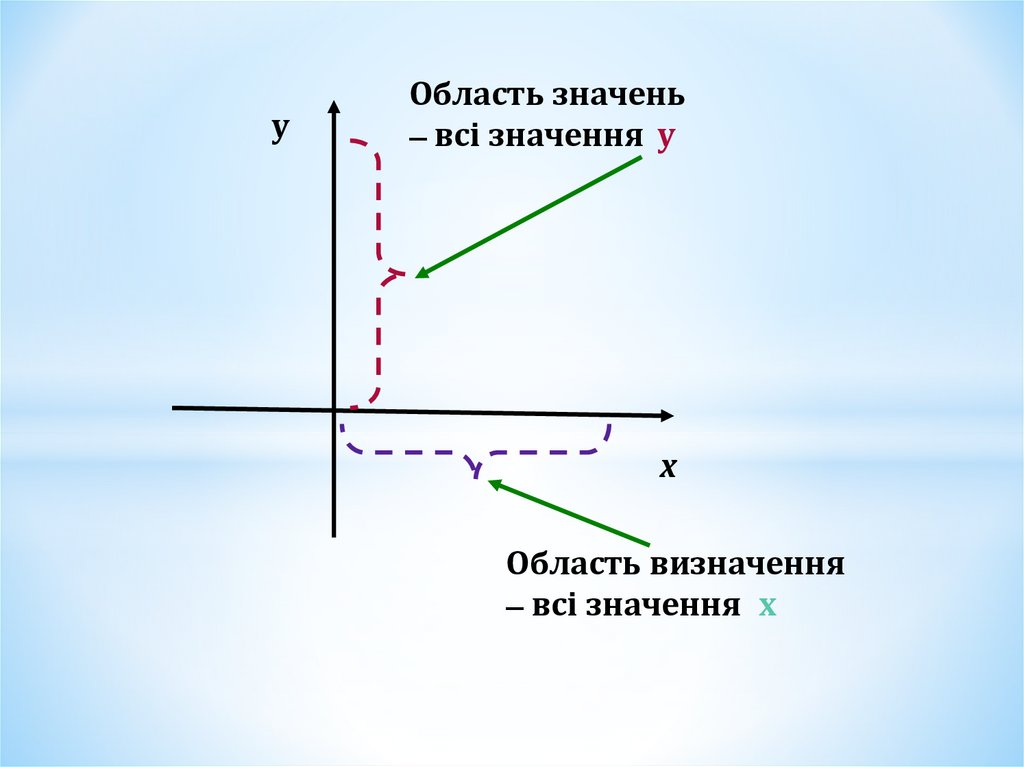
у
Область значень
– всі значення у
х
Область визначення
– всі значення х

11.

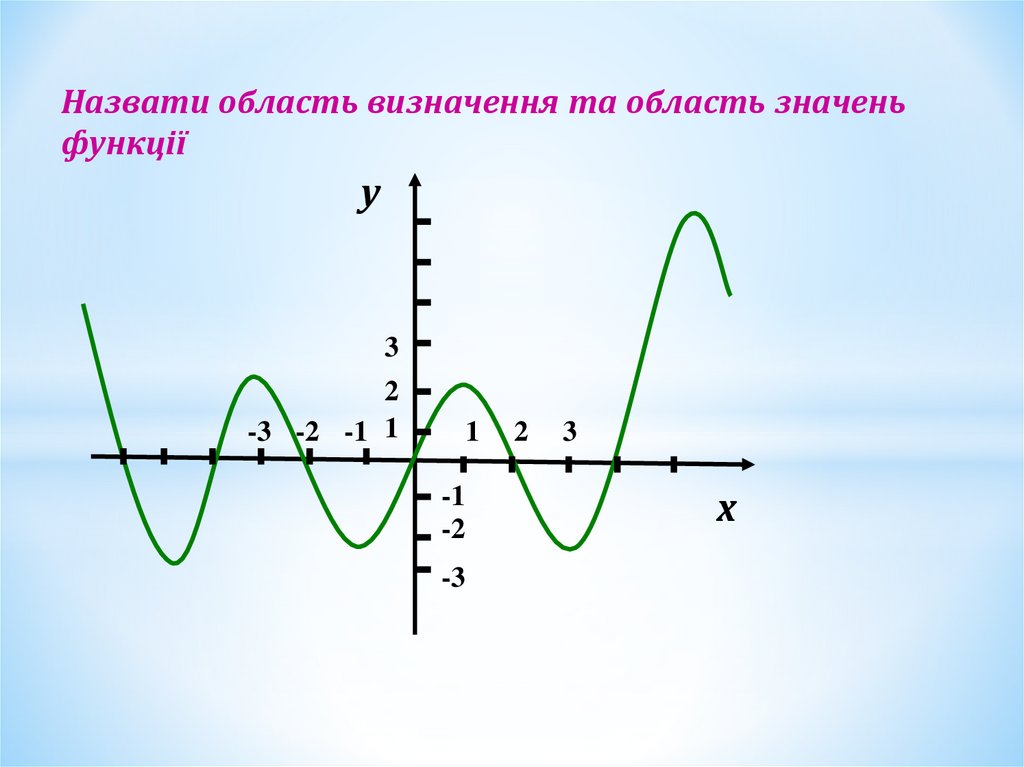
Назвати область визначення та область значень
функції
у
3
2
-3 -2 -1 1
1
-1
-2
-3
2
3
х

12. Види функцій

*

13. Лінійна функція

*
y = kx + b
Область
визначення,
D(y)
х є (-∞; +∞)
Область
значення,
E(y)
Якщо k ≠ 0, то
у є (-∞; +∞).
Якщо k = 0, то
у = b.
Графік
пряма

14. Обернена пропорційність

*
Область
визначення,
D(y)
х є (-∞; 0) U
(0; +∞)
Область
значення,
E(y)
у є (-∞; 0) U
(0; +∞)
Графік
гіпербола

15.

Область
визначення,
D(y)
х є (-∞; +∞)
Область
значення,
E(y)
у є [0; +∞)
Графік
парабола

16.

Область
визначення,
D(y)
х є [0; +∞)
Область
значення,
E(y)
у є [0; +∞)
Графік
вітка
параболи

17. Тренувальні вправи

*

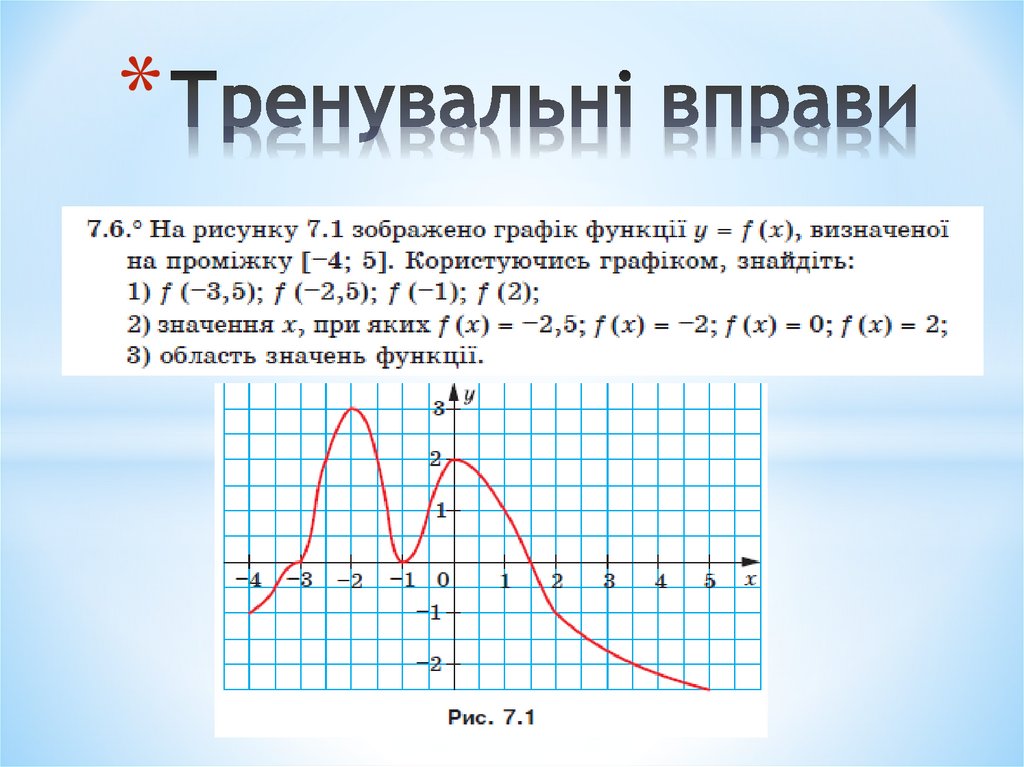
18. Тренувальні вправи

*

19. Тренувальні вправи

*

20. Тренувальні вправи

*

21. Тренувальні вправи

*

22. Тренувальні вправи

*

23. Домашнє завдання

* Домашнє завдання
1. Читати пункт 7.
2. Вивчити поняття.
3. Виконати № 7.2, № 7.7, № 7.9 (1-4)