Основы проективной геометрии. Система аксиом. Группы аксиом проективной геометрии. Лекция 6

1.

Аффинная и проективная геометрия_Лк-6
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Система аксиом. Группы аксиом проективной геометрии
На первой лекции был рассмотрен теоретикогрупповой подход к построению геометрии, в котором
отмечено, что группа преобразований метрической
(евклидовой)
геометрии
является
подгруппой
преобразований аффинной геометрии. Аффинная
группа преобразований входит как подгруппа в
проективную группу преобразований.
На этой лекции рассмотрим классический подход к
построению геометрии, который основывается на
классификации систем аксиом по Гильберту.

2.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Система аксиом. Группы аксиом проективной геометрии
Логическое построение геометрии было выполнено
еще Евклидом в третьем веке до нашей эры. Но
открытие неевклидовой геометрии в XIX веке
показало, что в системе аксиом Евклида имеются
изъяны. Исследование аксиоматики евклидовой
геометрии было завершено в конце XIX века Д.
Гильбертом. Система аксиом Д. Гильберта состоит из
пяти групп:
I – восьми аксиом принадлежности (соединения);
II – четырех аксиом порядка;
III – двух аксиом непрерывности;
IV – аксиомы о параллельных;
V – пяти аксиом конгруэнтности.

3.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Система аксиом. Группы аксиом проективной геометрии
Эти
аксиомы
сформулированы
относительно
объектов трех видов – точек, прямых, плоскостей и
трех видов отношений между ними, выражаемых
словами «принадлежит», «между», «конгруэнтен».
Аксиомы принадлежности (группа I) определяют
свойства взаимного расположения точек, прямых и
плоскостей, например:
– для любых двух точек A, B существует прямая a ,
принадлежащая каждой из этих двух точек A , B
– для двух точек A, B существует не более одной
прямой, принадлежащей каждой из точек A, B
и т.д., всего 8 аксиом

4.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Система аксиом. Группы аксиом проективной геометрии
Аксиомы порядка (группа II) выражают свойства
взаимного расположения точек на прямой и плоскости,
определяя термин «между»:
– если точка B лежит между точками A и C , то
A , B , C – различные точки и B лежит также
между точками C и A
– среди любых трех точек прямой существует
не более одной точки, лежащей между двумя
другими
и т.д., всего 4 аксиомы

5.

Аффинная и проективная геометрия
Система аксиом. Группы аксиом проективной геометрии
Аксиомы непрерывности (группа III) – две аксиомы
– пусть AB и CD – два каких-нибудь отрезка; тогда на прямой
AB существует конечное число таких точек A1, A2 ,..., An , что
отрезки AA1 , A1 A2 ,..., An 1 An конгруэнтны отрезку CD и точка
B лежит между A и An (аксиома Архимеда)
Аксиома
о
параллельных
(группа
IV),
с
евклидовой точки зрения гласит: через точку,
расположенную вне данной прямой, можно
провести не более одной прямой, параллельной ей
Аксиомы конгруэнтности (группа V), определяют
понятие равенства для отрезков и углов - пять аксиом
– если два отрезка конгруэнтны третьему,
то они конгруэнтны друг другу

6.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Система аксиом. Группы аксиом проективной геометрии
Три требования, предъявляемых
к системам аксиом:
– непротиворечивость, набор аксиом должен быть
логически не противоречивым, т.е. из них путем
логических рассуждений не должны получаться два
взаимно исключающих следствия;
– независимость, или неизбыточность, какиелибо аксиомы не должны выводится из остальных;
– полнота, система не должна допускать
пополнения новыми аксиомами, не противоречащими
уже принятым и не вытекающими из них.

7.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Система аксиом. Группы аксиом проективной геометрии
группы аксиом I, II, III определяют
аксиоматику проективной
геометрии;
группы аксиом I, II, III, IV
определяют аксиоматику
аффинной геометрии;
все пять групп аксиом –
метрическую, или элементарную
(евклидову) геометрию.

8.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные геометрические формы проективной
геометрии
В проективной геометрии фигуры принято называть
формами. Они бывают линейными, или основными,
например прямая, плоскость, пространство, и
нелинейными, например кривая линия, поверхность.
Эти формы можно рассматривать как некоторое
множество точек. Поэтому принято называть линию
рядом точек, плоскость – полем точек. В некоторых
случаях плоскость и пространство рассматривают не
как множество точек, а как множество прямых. Тогда
они называются соответственно полем прямых,
пространством прямых, или линейчатым
пространством

9.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные геометрические формы проективной
геометрии
Формы
принято
классифицировать
по
их
размерности.
Формы,
состоящие
из
однопараметрического
множества ( 1 ) точек, прямых, плоскостей, называются
формами 1-й ступени, из двухпараметрического
множества ( 2 ) – формами 2-й ступени и т. д.
(однопараметрические
многообразия,
двухпараметрические многообразия и т. д.).
Две какие-либо формы, которые можно привести во
взаимно однозначное соответствие, имеют равные
размерности. Этим правилом пользуются для получения
новых форм данной ступени путем проецирования
простейших форм этой ступени.

10.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные геометрические формы проективной
геометрии
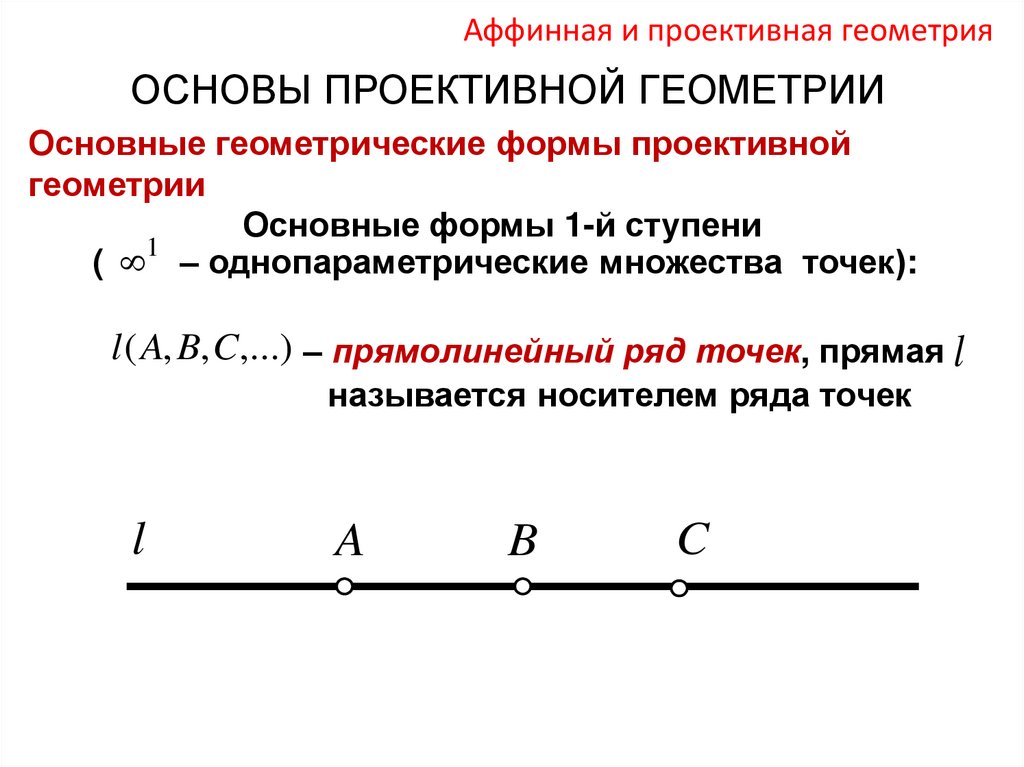
Основные формы 1-й ступени
1
( – однопараметрические множества точек):
l ( A, B, C,...) – прямолинейный ряд точек, прямая l
называется носителем ряда точек
l
A
B
C

11.

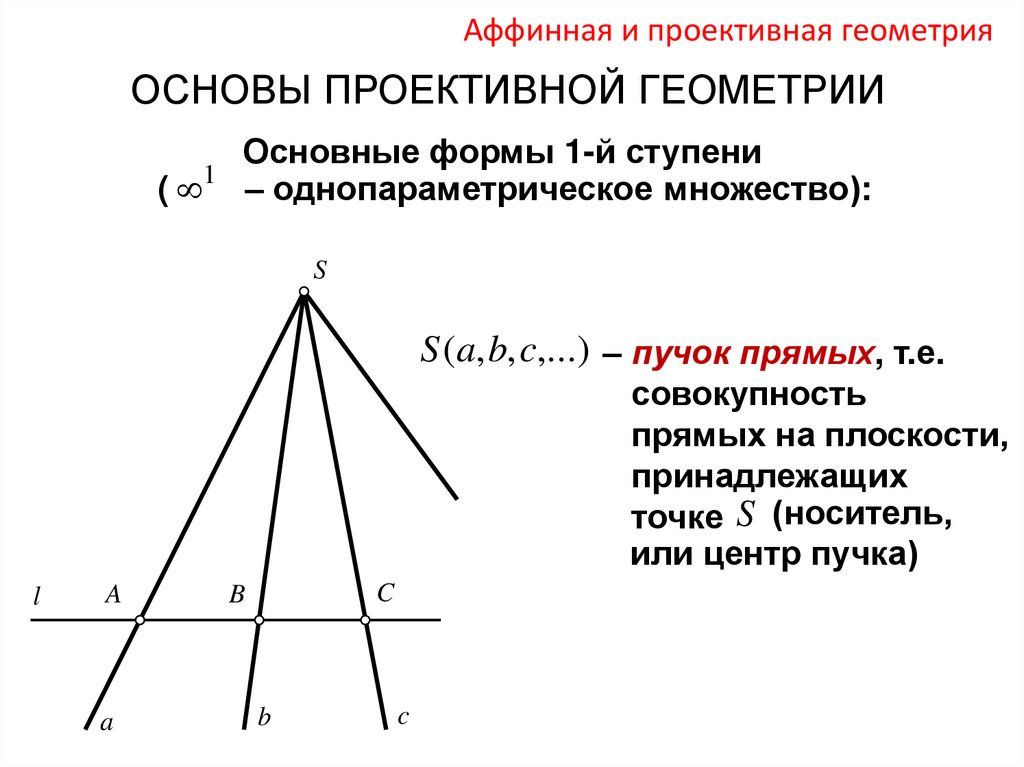
Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
(
1
Основные формы 1-й ступени
– однопараметрическое множество):
S
S (a, b, c,...) – пучок прямых, т.е.
совокупность
прямых на плоскости,
принадлежащих
точке S (носитель,
или центр пучка)
l
A
a
C
B
b
c

12.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 1-й ступени
1
( – однопараметрическое множество):
s( , , ,...)
– пучок плоскостей т.е.
совокупность
плоскостей,
принадлежащих данной прямой
s (носитель пучка, или ось пучка).
s
l

13.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 1-й ступени
1
( – однопараметрическое множество):
Прямая линия (числовая ось), или ряд точек
содержит однопараметрическое множество точек,
так как любая ее точка определяется заданием
одной координаты.
l
A
B
C

14.

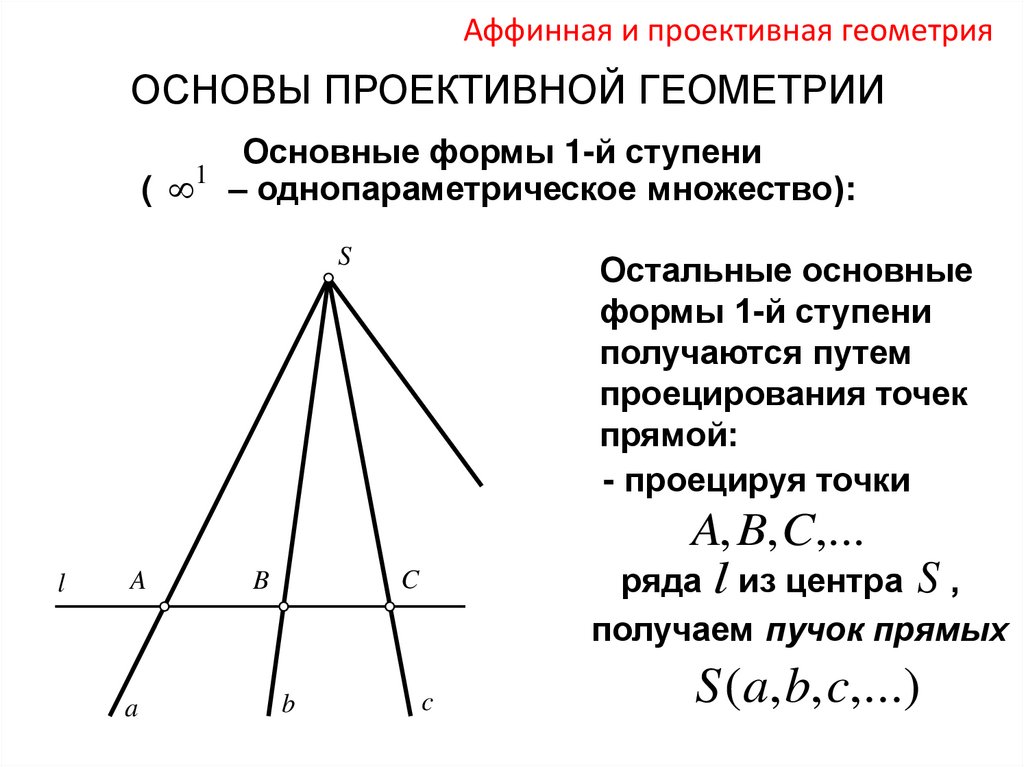
Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 1-й ступени
1
( – однопараметрическое множество):
S
l
A
Остальные основные
формы 1-й ступени
получаются путем
проецирования точек
прямой:
- проецируя точки
A, B, C,...
ряда l из центра S ,
C
B
получаем пучок прямых
a
b
c
S (a, b, c,...)

15.

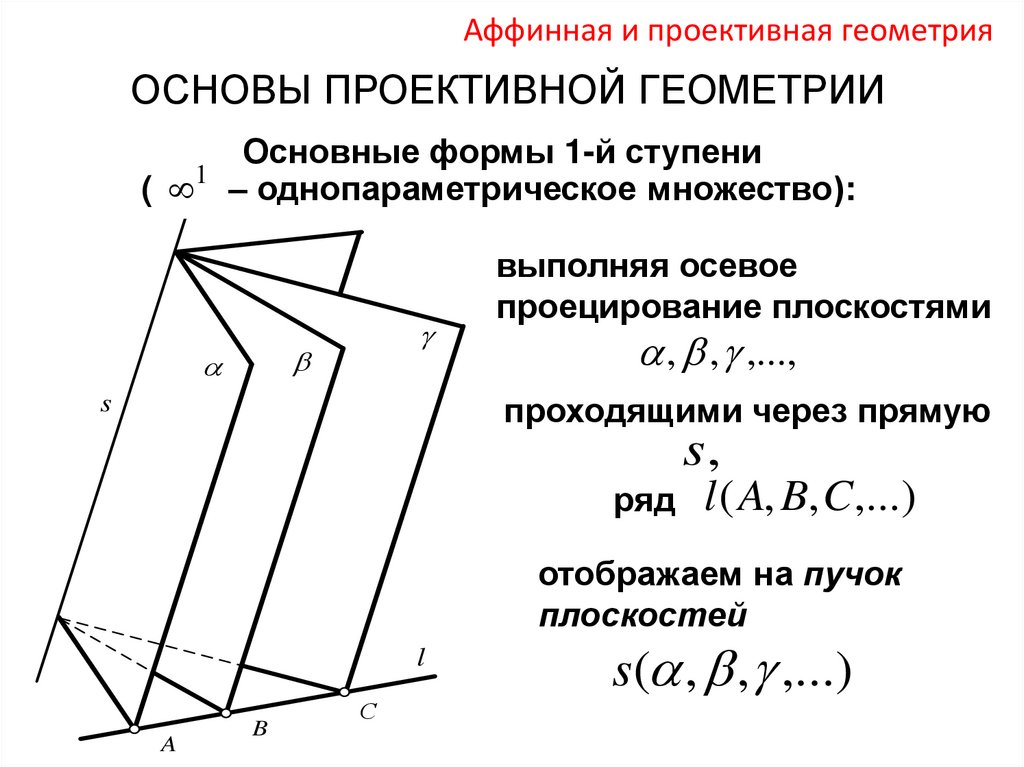
Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 1-й ступени
1
( – однопараметрическое множество):
выполняя осевое
проецирование плоскостями
, , ,...,
проходящими через прямую
s
s,
ряд
l ( A, B, C,...)
отображаем на пучок
плоскостей
l
A
B
С
s( , , ,...)

16.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
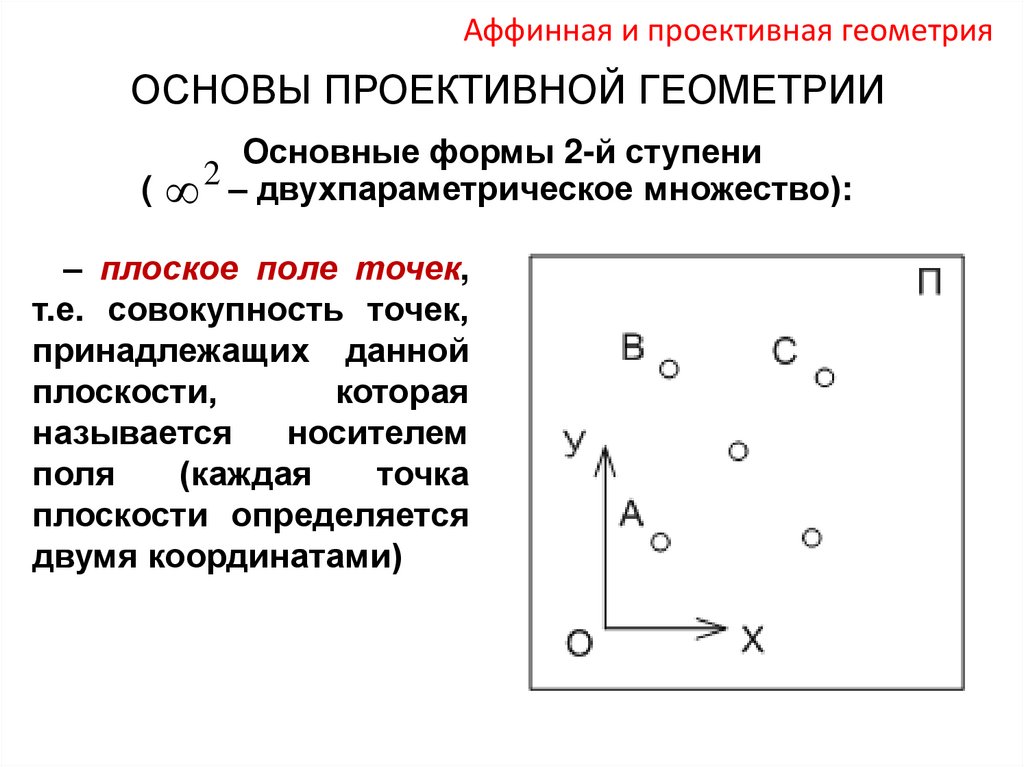
Основные формы 2-й ступени
( 2 – двухпараметрическое множество):
– плоское поле точек,
т.е. совокупность точек,
принадлежащих данной
плоскости,
которая
называется
носителем
поля
(каждая
точка
плоскости определяется
двумя координатами)

17.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 2-й ступени
( 2 – двухпараметрическое множество):
– плоское поле прямых,
т.е. совокупность прямых,
принадлежащих
данной
плоскости,
которая
называется
носителем
поля

18.

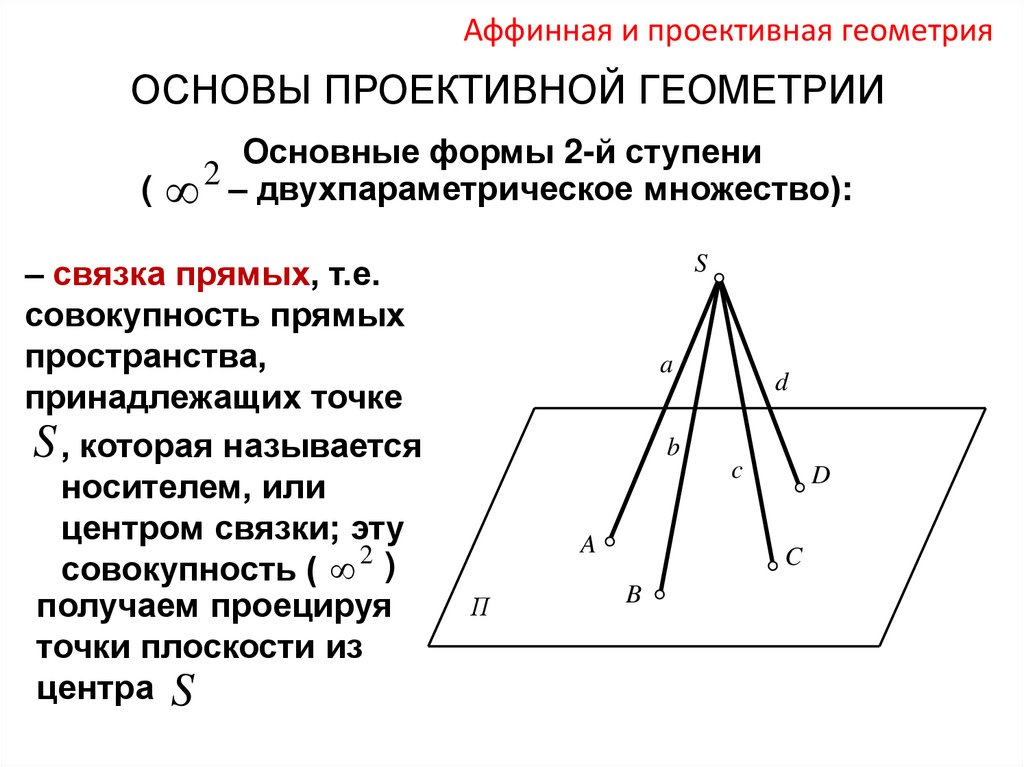
Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 2-й ступени
( 2 – двухпараметрическое множество):
– связка прямых, т.е.
совокупность прямых
пространства,
принадлежащих точке
S , которая называется
носителем, или
центром связки; эту
совокупность ( 2 )
получаем проецируя
точки плоскости из
центра S
S
a
b
A
П
d
c
D
C
B

19.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 2-й ступени
( 2 – двухпараметрическое множество):
– связка плоскостей, т.е. совокупность плоскостей
пространства, принадлежащих точке S , которая
называется носителем, или центром связки;
эту совокупность ( 2 ) получаем, проецируя
прямые плоскости из центра S

20.

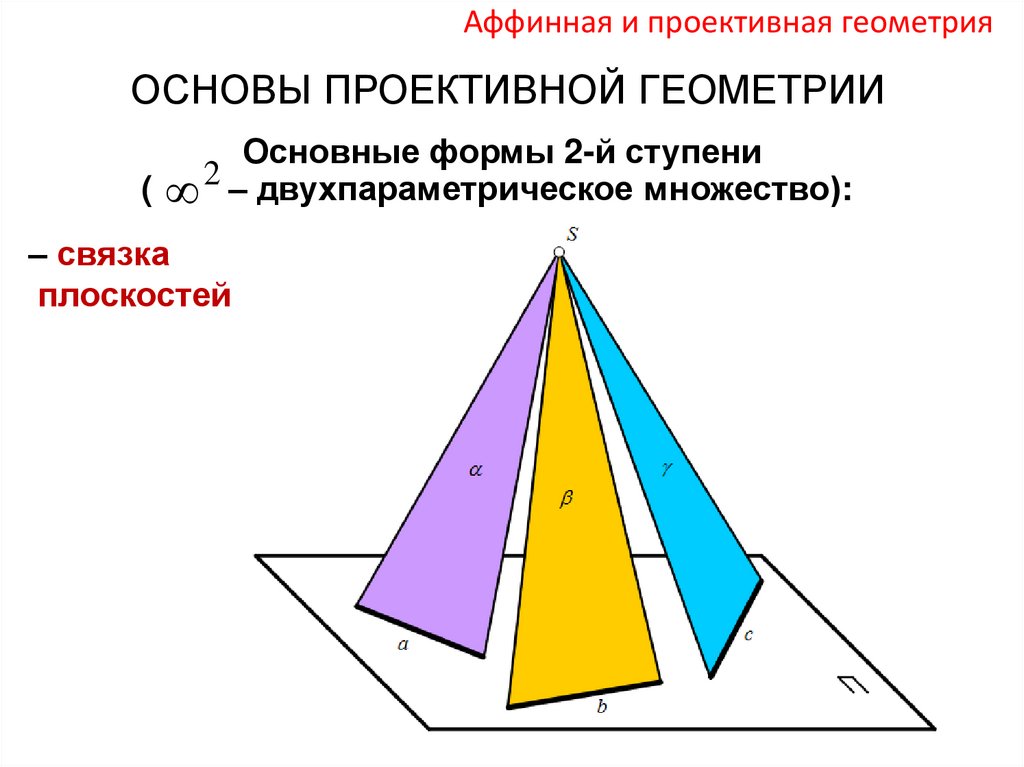
Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Основные формы 2-й ступени
( 2 – двухпараметрическое множество):
– связка
плоскостей

21.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
( 3
Основные формы 3-й ступени
– трехпараметрическое множество):
– пространство точек, как совокупность всех точек
проективного пространства, которое в данном случае
играет роль носителя точек (точка в пространстве
определяется заданием трех координат);
– пространство плоскостей, т.е. совокупность всех
плоскостей проективного пространства, которое в
данном случае является носителем плоскостей.

22.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
3
(
Основные формы 3-й ступени
– трехпараметрическое множество):
Для примера выполним расчет параметрического
числа плоскости трехмерного пространства.
Параметрическое число плоскости, принадлежащей
трехмерному пространству, равно числу независимых
коэффициентов в общем уравнении плоскости:
Ax By Cz D 0
В этом уравнении свободный член D
можно приравнять к единице, поделив на него все
коэффициенты. Тогда остаются три независимых
коэффициента, поэтому параметрическое число
плоскости равно трем ( 3 ).

23.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Принцип двойственности
Следующая важная особенность, которую
необходимо знать при изучении геометрии, –
это проявление принципа двойственности,
то есть когда в любом предложении,
сформулированным относительно
подпространств проективного
пространства, перестановка местами пар
подпространств равных размерностей не
нарушает справедливости этого
предложения.

24.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Принцип двойственности
Так для двумерного проективного пространства
принцип
двойственности
гласит:
любое
предложение, сформулированное относительно
точек и прямых проективной плоскости, остается
справедливым, если в нем заменить слово «точка»
словом «прямая», а слово «прямая» – словом
«точка». Так, например, две известные аксиомы
соединения (принадлежности) гласят:
– две различные точки принадлежат одной
прямой;
– две различные прямые принадлежат одной
точке.

25.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Принцип двойственности
Этот
принцип
для
трехмерного
пространства
читается
так:
любое
предложение,
сформулированное
относительно точек, прямых и плоскостей
трехмерного проективного пространства,
остается справедливым, если в нем
заменить
слово
«точка»
словом
«плоскость», слово «плоскость» – словом
«точка», а слово «прямая» оставить без
изменения.

26.

Аффинная и проективная геометрия
ОСНОВЫ ПРОЕКТИВНОЙ ГЕОМЕТРИИ
Принцип двойственности
Примером могут служить две другие аксиомы
соединения (принадлежности):
– три различные точки, не принадлежащие одной
прямой, принадлежат одной плоскости;
– три различные плоскости, не принадлежащие
одной прямой, принадлежат одной точке.
Такие симметричные понятия, аксиомы и теоремы в
проективной геометрии называются двойственными.
При этом слово “принадлежит” нужно заменить
словом “проходит” или воспользоваться словом –
инцидентна.

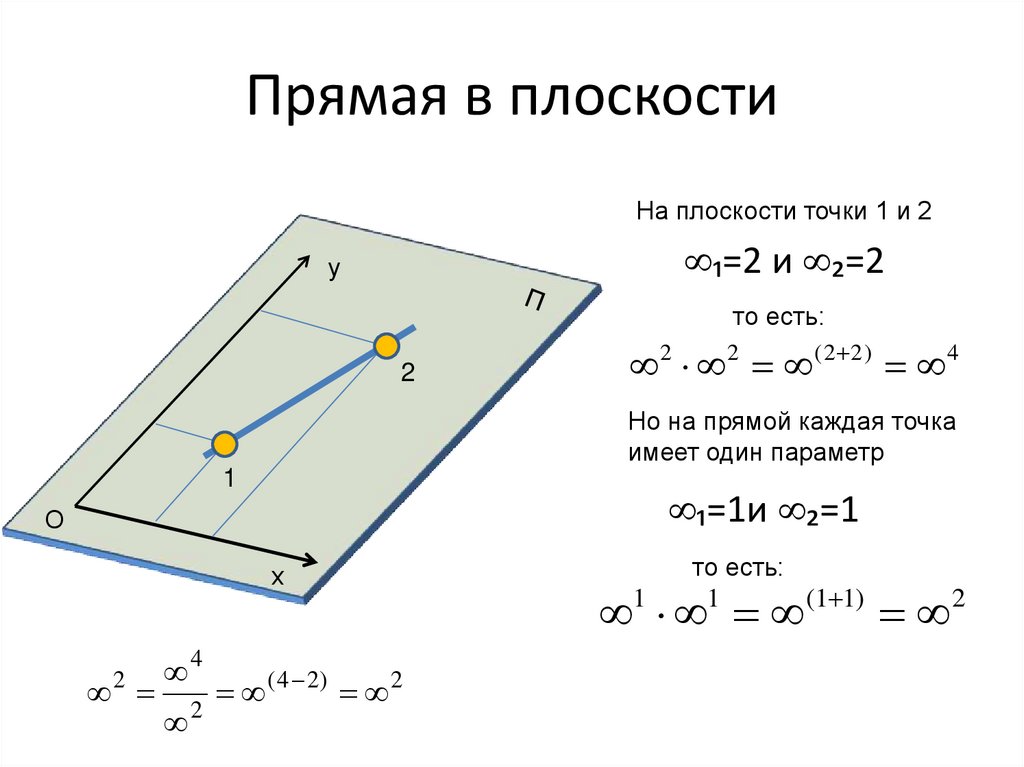
27. Прямая в плоскости

На плоскости точки 1 и 2
₁=2 и ₂=2
у
то есть:
2
2 2 ( 2 2 ) 4
Но на прямой каждая точка
имеет один параметр
1
₁=1и ₂=1
О
х
2
4
( 4 2)
2
2
то есть:
1
(1 1)
1
2