Similar presentations:
Лекция 06. Основные понятия проективной геометрии (продолжение)
1.
Основные понятияпроективной геометрии
(продолжение)
2.
1. Некоторыевоспоминания
2
3.
Евклидоваплоскость
Аффинная
плоскость
Проективная
плоскость
3
4.
Евклидоваплоскость
Евклидова
геометрия
Аффинная
плоскость
Аффинная
геометрия
Проективная
плоскость
Проективная
геометрия
4
5.
Проективные свойства(инварианты)
5
6.
Проективные свойства(инварианты)
инцидентность
коллинеарность
конкуррентность
6
7.
2. Принципдвойственности
7
8.
Взаимно-двойственные элементыточка
прямая
8
9.
Взаимно-двойственные элементыточка
прямая
Взаимно-двойственные операции
провести прямую через точку
отметить точку на прямой
9
10.
Пример замены «точка ↔ прямая»Через две различные
точки можно
провести
единственную
прямую
10
11.
Пример замены «точка ↔ прямая»Через две различные
точки можно
провести
единственную
прямую
Через две различные
прямые можно
провести
единственную
точку
11
12.
Пример замены «точка ↔ прямая»Через две различные
точки можно
провести
единственную
прямую
Через две различные
прямые можно
провести
единственную
точку
Две различные
точки
инцидентны
единственной прямой
12
13.
Пример замены «точка ↔ прямая»Через две различные
точки можно
провести
единственную
прямую
Через две различные
прямые можно
провести
единственную
точку
Две различные
точки
инцидентны
единственной прямой
Две различные
прямые
инцидентны
единственной точке
13
14.
Пример замены «точка ↔ прямая»Через две различные
точки можно
провести
единственную
прямую
Через две различные
прямые можно
провести
единственную
точку
Две различные
точки
инцидентны
единственной прямой
Две различные
прямые
инцидентны
единственной точке
14
15.
Принцип двойственностиИз каждого проективного предложения
относительно точек и прямых на плоскости
может быть получено второе предложение
путём замены
слова «точка» словом «прямая»
и наоборот.
Жан Виктор Понселе
офицер инженерного корпуса.
Написано в г.Саратове
в 1812-1815 г.г.
15
16.
Принцип двойственностиДве фигуры взаимно
двойственны,
если одна может быть
получена из другой
посредством замены
каждого элемента и
каждой операции
двойственным элементом
и двойственной
операцией.
16
17.
Принцип двойственностиДве теоремы взаимно
двойственны,
если одна превращается в
другую
при замене каждого
элемента
и каждой операции
двойственным элементом
и двойственной
операцией.
17
18.
Принцип двойственностиЯвление двойственности
резко отличает
проективную геометрию
от элементарной
(метрической),
в которой никакой
двойственности не
наблюдается.
18
19.
Принцип двойственностиЯвление двойственности
резко отличает
проективную геометрию
от элементарной
(метрической),
в которой никакой
двойственности не
наблюдается.
Например, бессмысленно
искать какое-нибудь
19
20.
Принцип двойственностиКаждой верной теореме
проективной геометрии
сопоставляется
двойственная ей,
также верная теорема.
20
21.
Принцип двойственностиКаждой верной теореме
проективной геометрии
сопоставляется
двойственная ей,
также верная теорема.
Следствие. Двойственную
теорему
можно не
доказывать.
21
22.
Перспективность относительно точкиЕсть две конфигурации из
точек
(могут быть и проходящие
через них прямые).
22
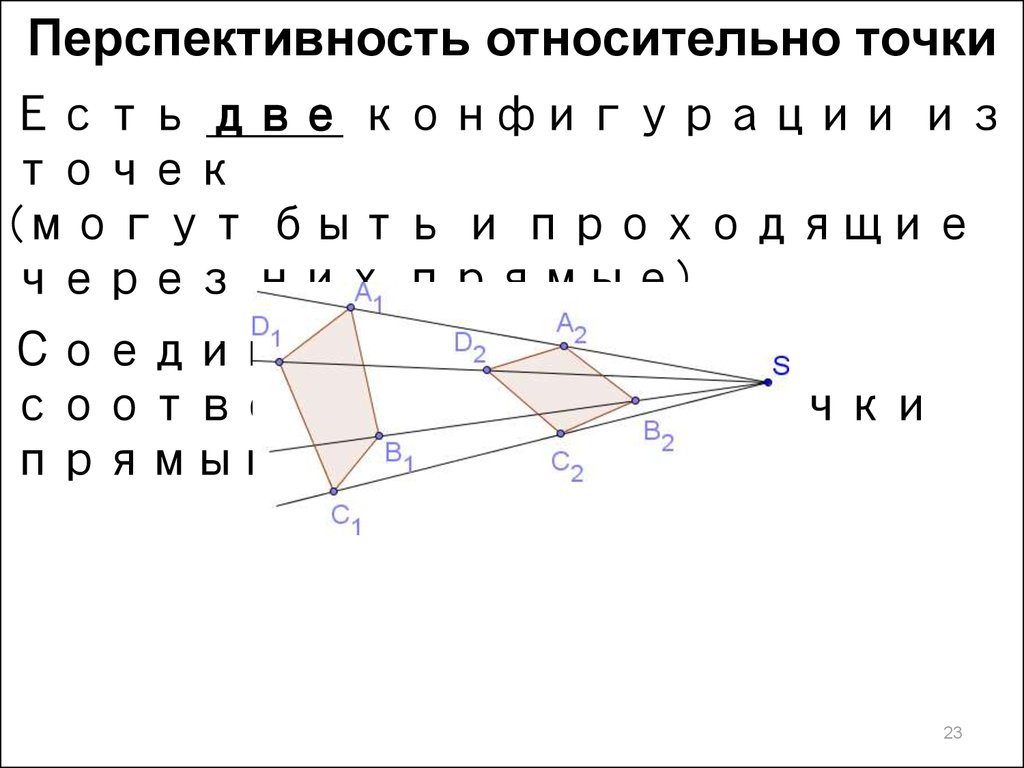
23.
Перспективность относительно точкиЕсть две конфигурации из
точек
(могут быть и проходящие
через них прямые).
Соединим
соответствующие точки
прямыми попарно.
23
24.
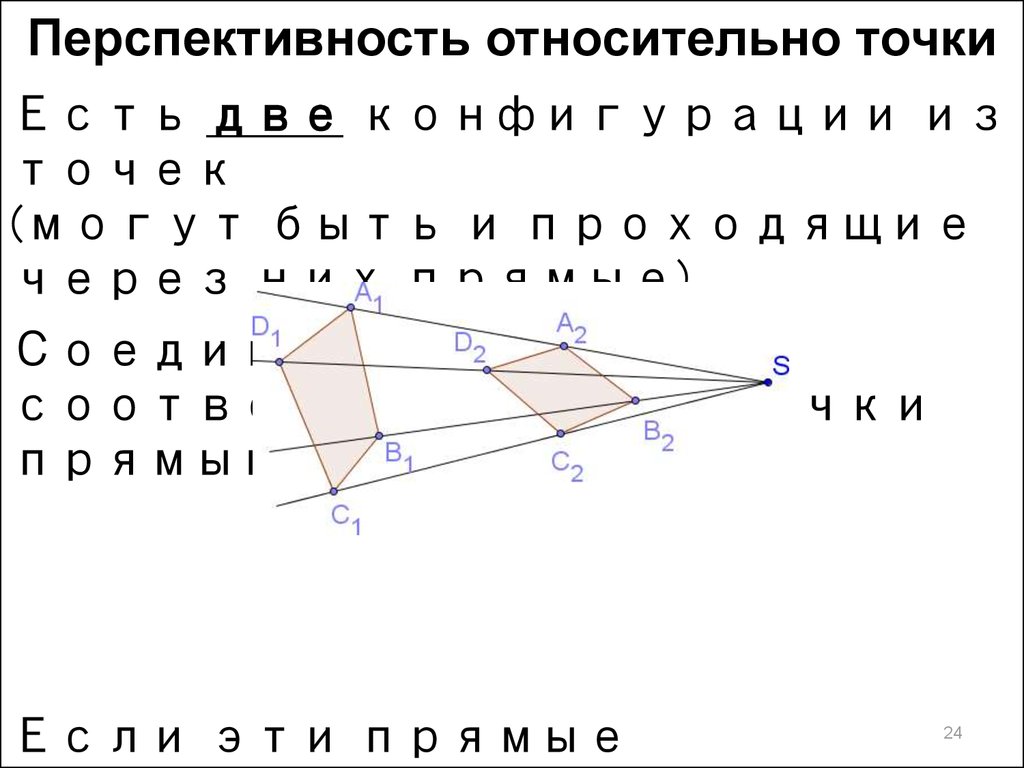
Перспективность относительно точкиЕсть две конфигурации из
точек
(могут быть и проходящие
через них прямые).
Соединим
соответствующие точки
прямыми попарно.
Если эти прямые
24
25.
Перспективность относительно прямойЕсть две конфигурации из
прямых
(могут быть выделены
точки их пересечения).
25
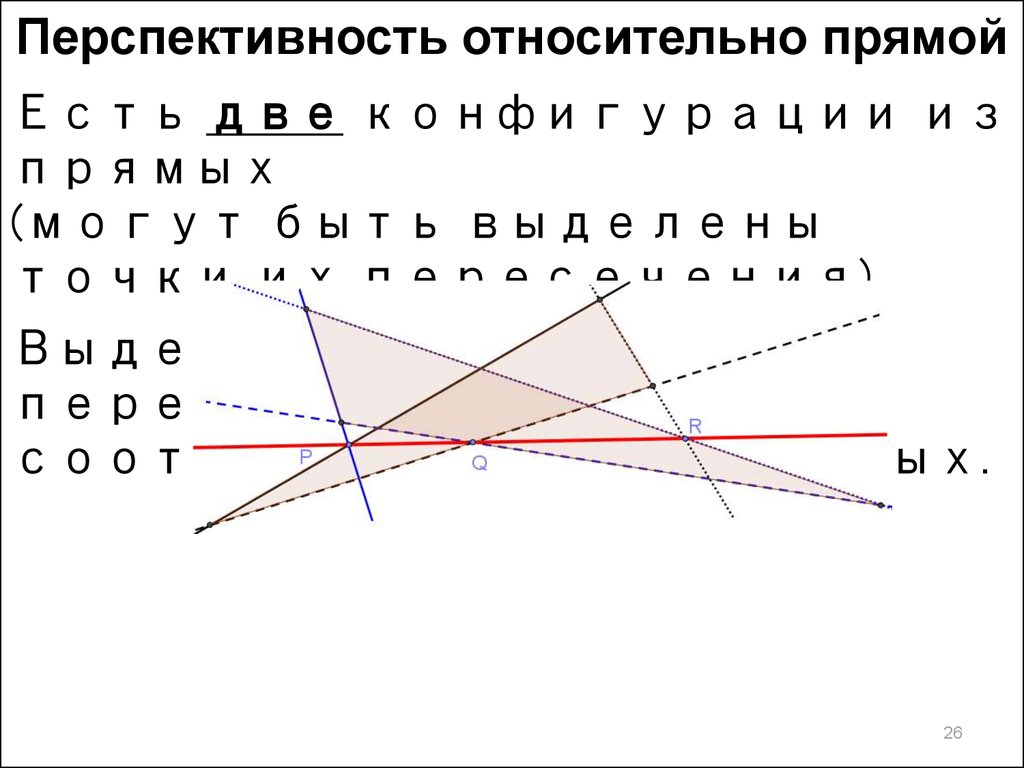
26.
Перспективность относительно прямойЕсть две конфигурации из
прямых
(могут быть выделены
точки их пересечения).
Выделим точки
пересечения
соответствующих прямых.
26
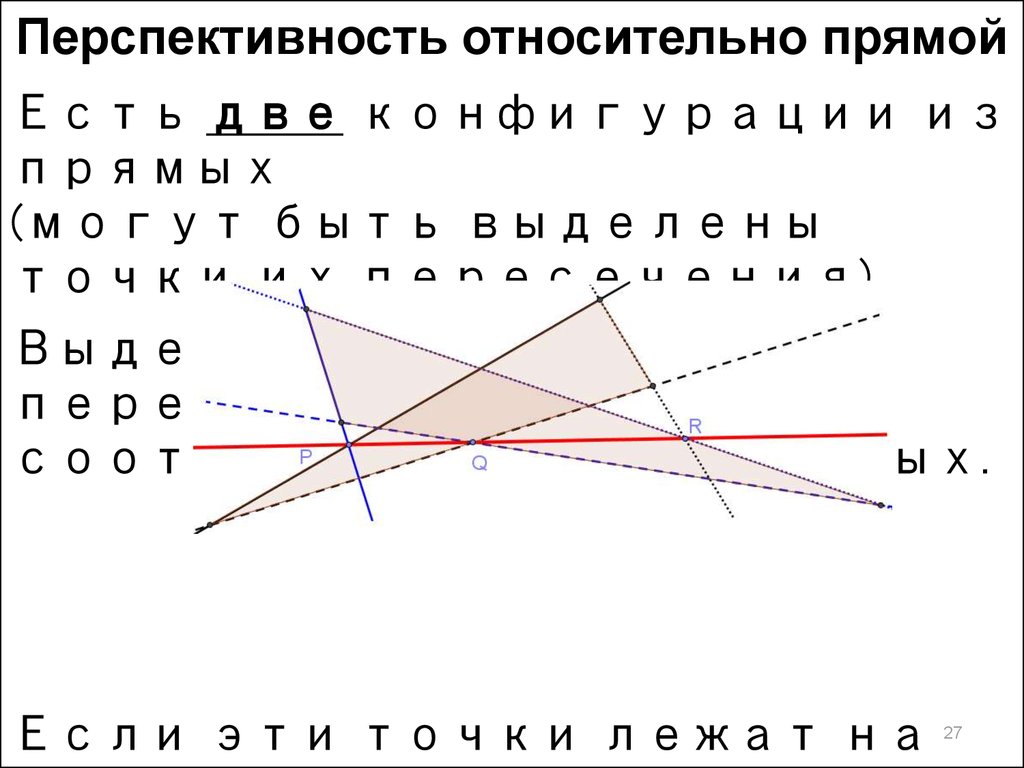
27.
Перспективность относительно прямойЕсть две конфигурации из
прямых
(могут быть выделены
точки их пересечения).
Выделим точки
пересечения
соответствующих прямых.
Если эти точки лежат на
27
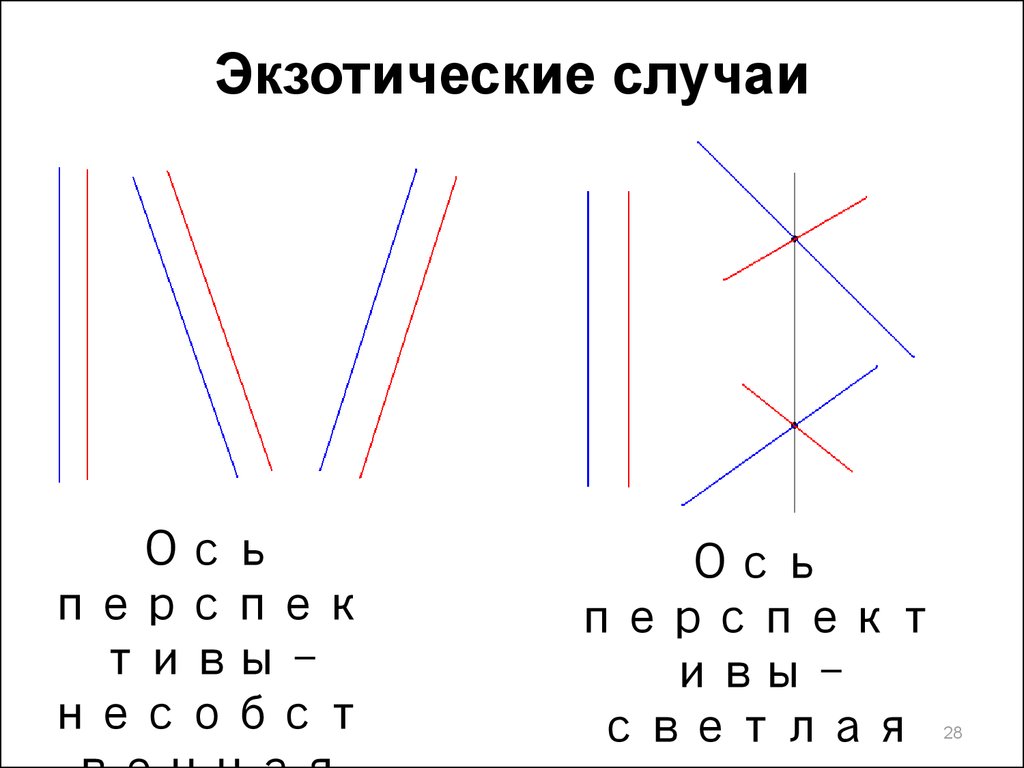
28. Экзотические случаи
Осьперспек
тивы –
несобст
Ось
перспект
ивы –
светлая
28
29.
Пример. Теорема ДезаргаЕсли два треугольника
перспективны
относительно точки, то
три точки пересечения
соответствующих
их сторон
коллинеарны.
29
30.
Пример. Теорема ДезаргаЕсли два треугольника
перспективны
относительно точки, то
три точки пересечения
соответствующих
их сторон
коллинеарны.
Если два треугольника
перспективны
относительно прямой, то
три прямые, проходящие
через соответствующие
их вершины
конкуррентны.
30
31.
Пример. Теорема ДезаргаЕсли два треугольника
перспективны
относительно точки, то
три точки пересечения
соответствующих
их сторон
коллинеарны.
Если два треугольника
перспективны
относительно прямой, то
три прямые, проходящие
через соответствующие
их вершины
конкуррентны.
31
32.
Пример. Теорема ДезаргаЕсли два треугольника
перспективны
относительно точки,
то они перспективны и
относительно прямой.
32
33.
Пример. Теорема ДезаргаЕсли два треугольника Если два треугольника
перспективны
перспективны
относительно точки,
относительно прямой,
то они перспективны и то они перспективны и
относительно прямой.
относительно точки.
33
34.
Вспомогательные теоремы34
35.
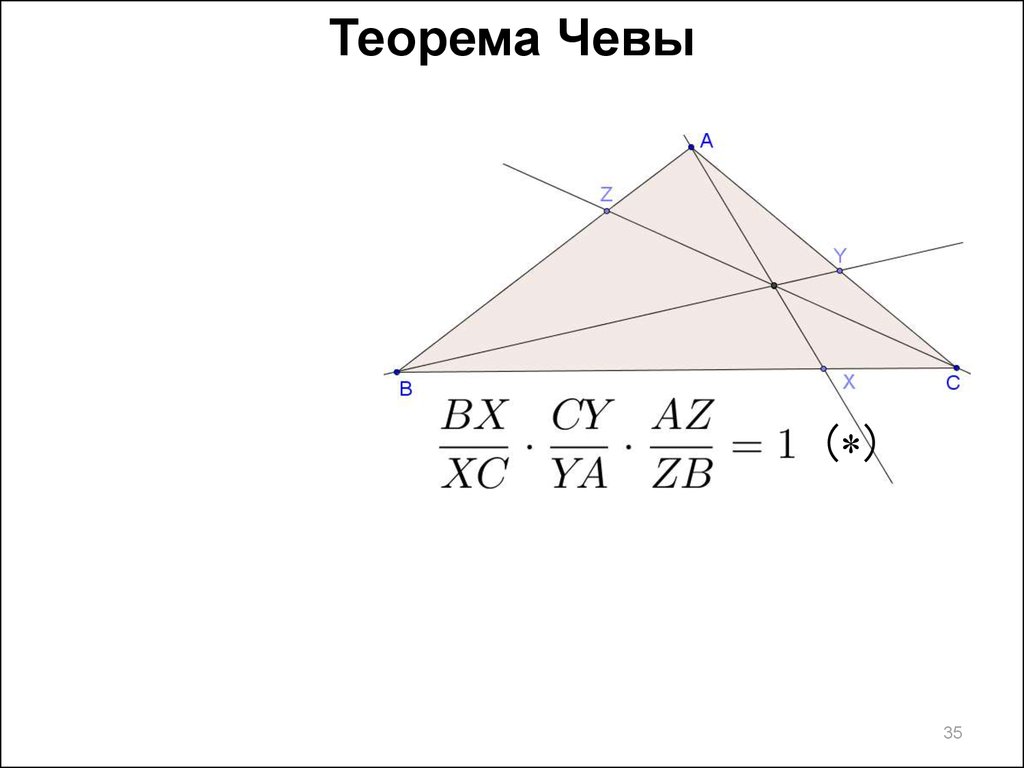
Теорема Чевы( )
35
36.
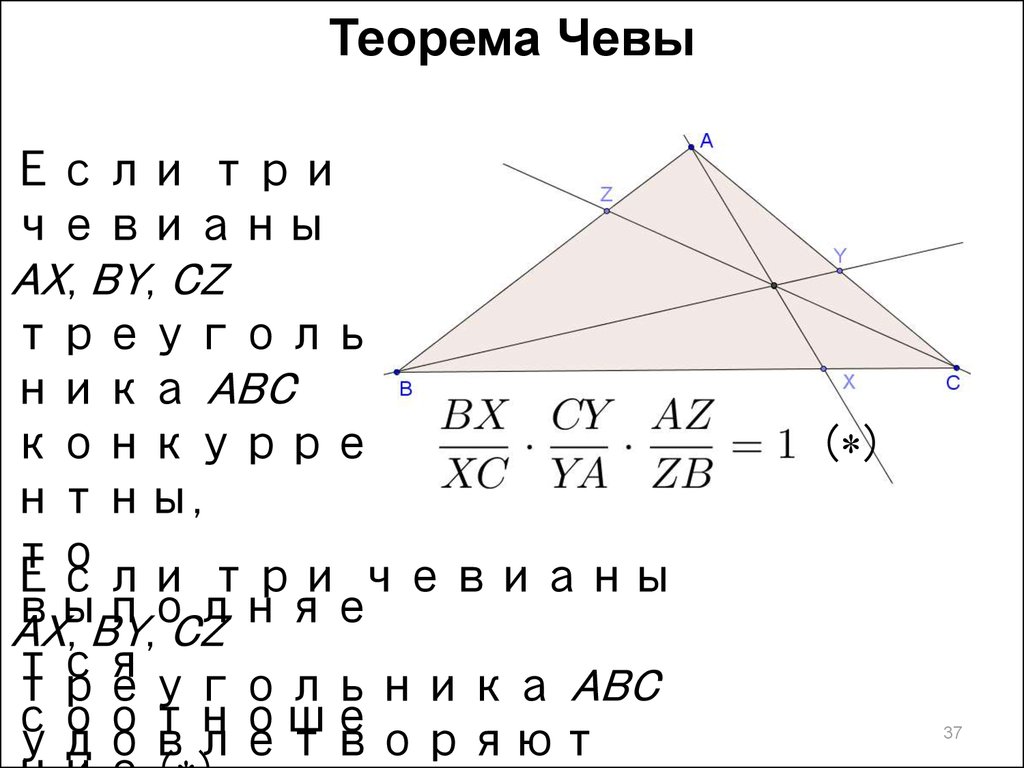
Теорема ЧевыЕсли три
чевианы
AX, BY, CZ
треуголь
ника ABC
конкурре
нтны,
то
выполняе
тся
соотноше
( )
36
37.
Теорема ЧевыЕсли три
чевианы
AX, BY, CZ
треуголь
ника ABC
конкурре
нтны,
то
Если три чевианы
выполняе
AX, BY, CZ
тся
треугольника ABC
соотноше
удовлетворяют
( )
37
38.
Теорема Менелая( )
38
39.
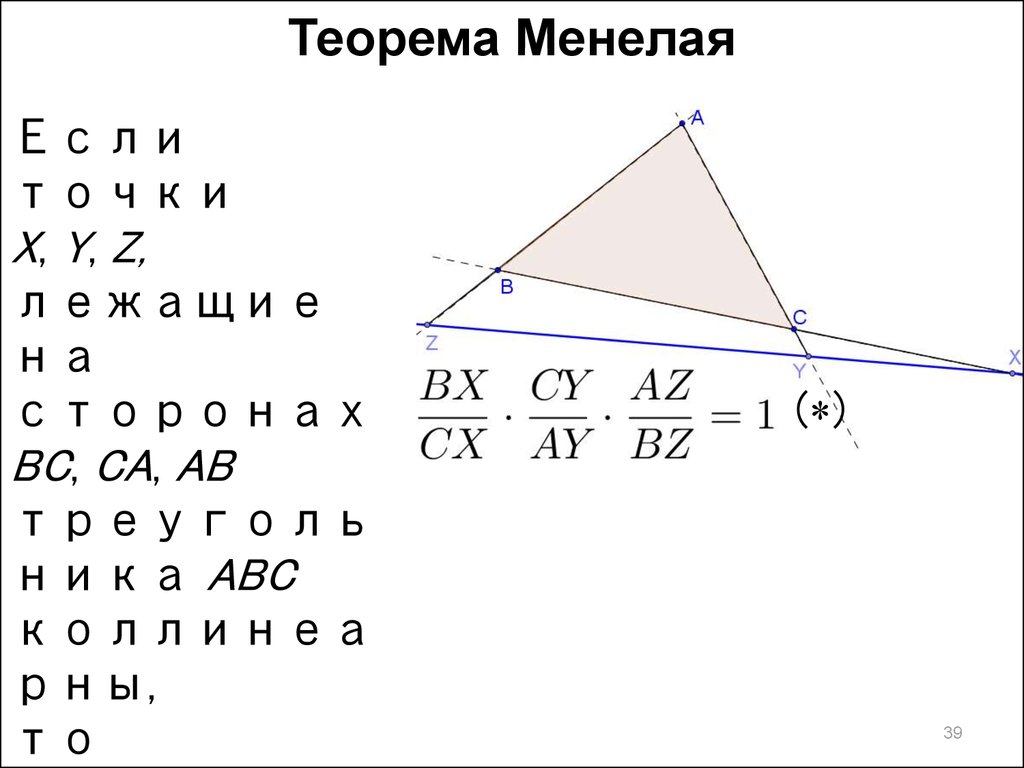
Теорема МенелаяЕсли
точки
X, Y, Z,
лежащие
на
сторонах
BC, CA, AB
треуголь
ника ABC
коллинеа
рны,
то
( )
39
40.
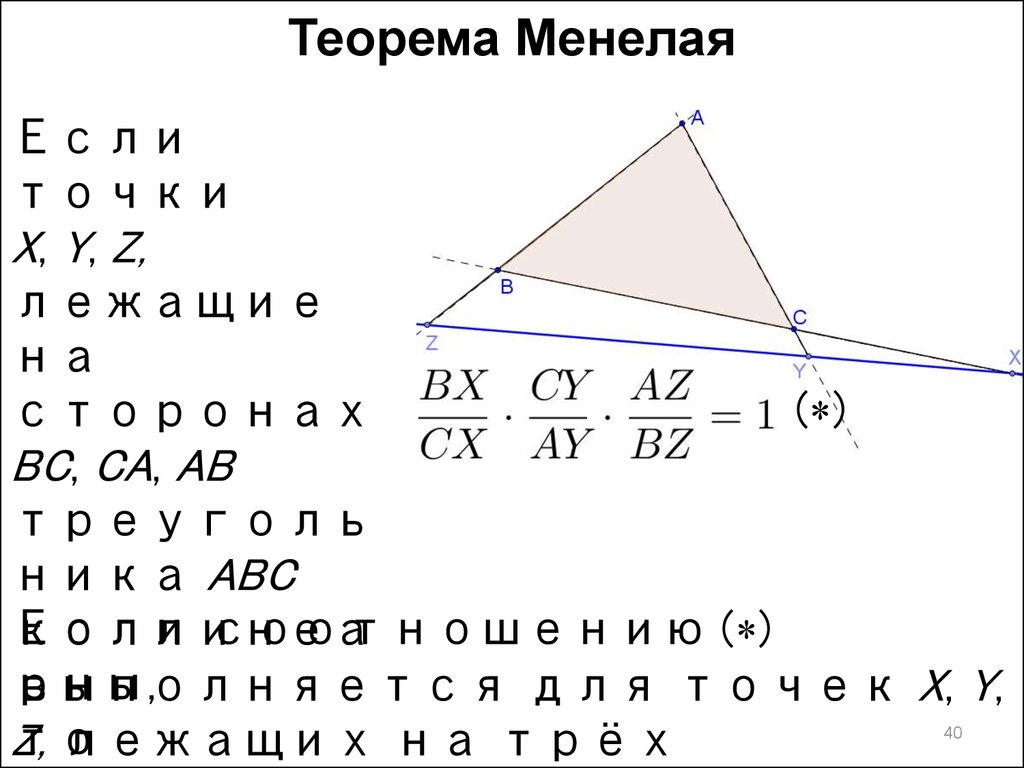
Теорема МенелаяЕсли
точки
X, Y, Z,
лежащие
на
( )
сторонах
BC, CA, AB
треуголь
ника ABC
Если
соотношению ( )
коллинеа
рны,
выполняется для точек X, Y,
то
Z,
лежащих на трёх
40
41.
РезюмеТеорема Чевы – критерий
конкуррентности.
Теорема Менелая –
критерий
коллинеарности.
41
42.
Домашнее заданиеДоказать теоремы
Чевы и Менелая
(прямую и обратную).
42
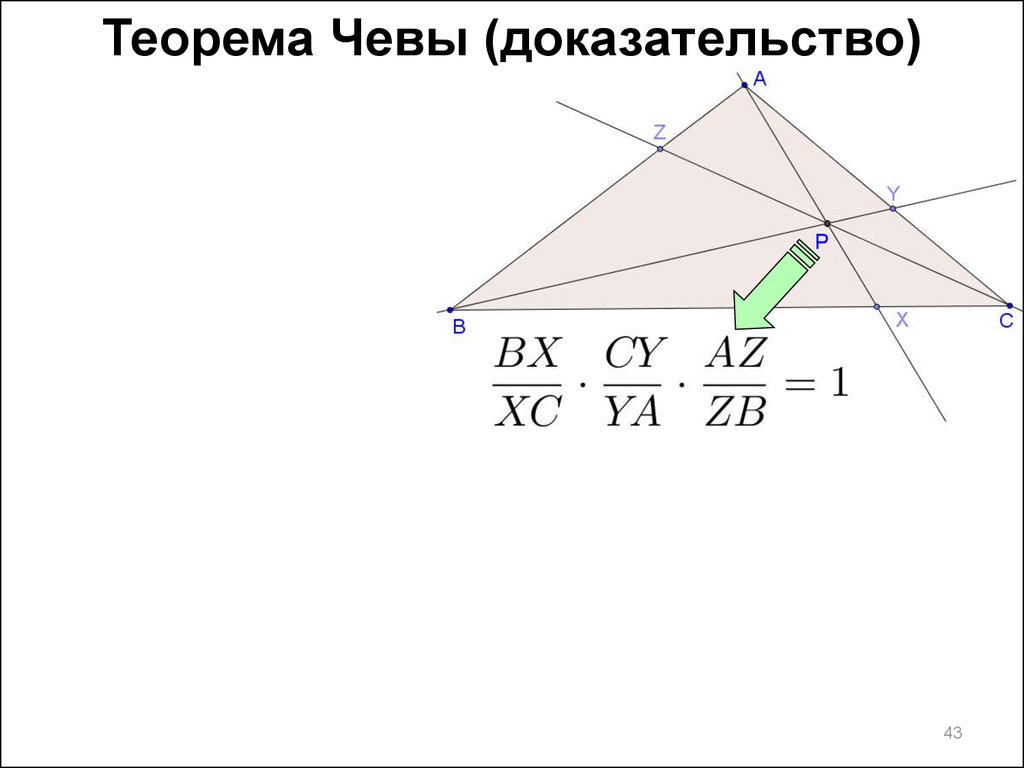
43.
Теорема Чевы (доказательство)P
43
44.
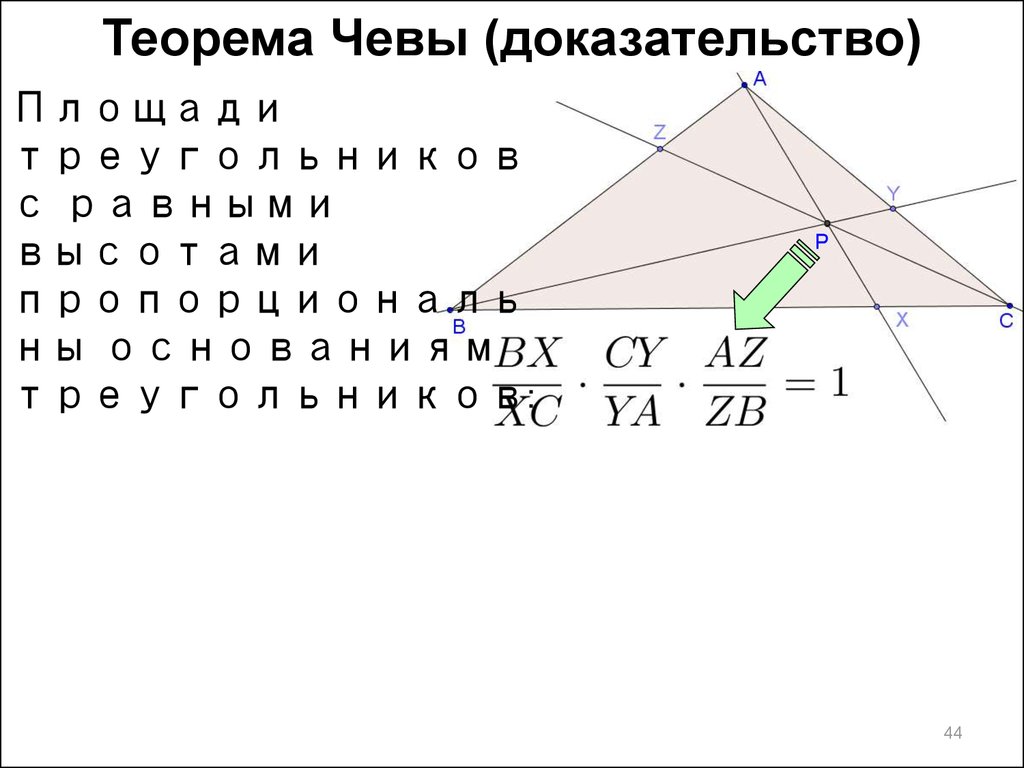
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
треугольников:
P
44
45.
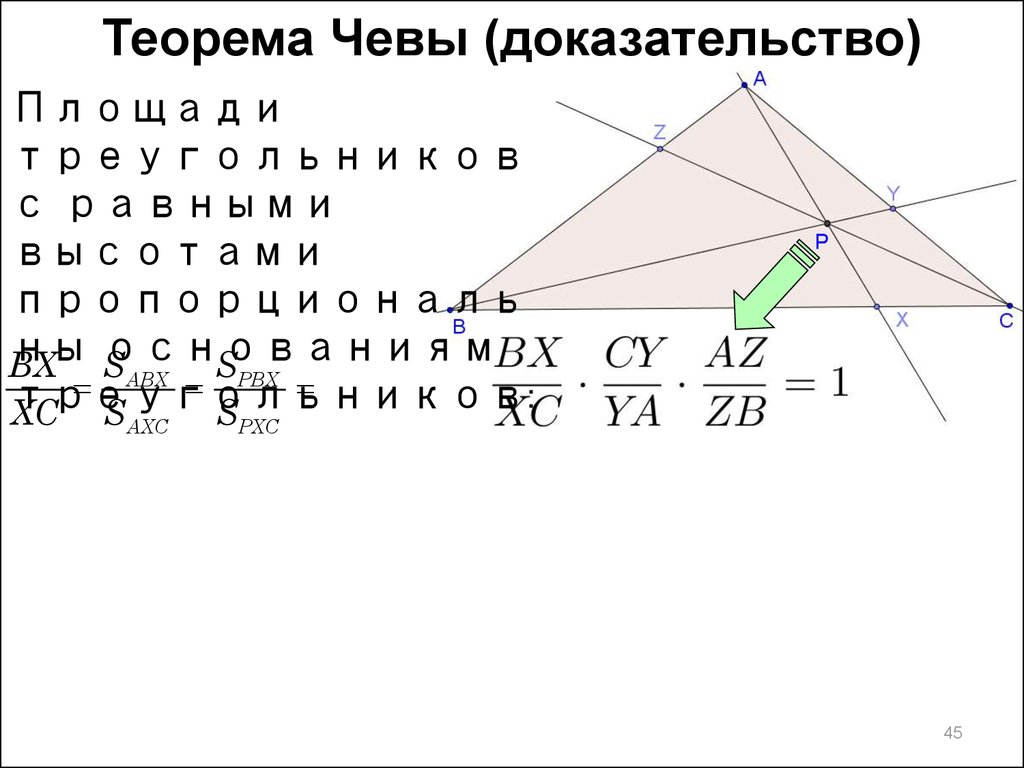
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
BX
SABX SPBX
треугольников:
XC S
S
AXC
P
PXC
45
46.
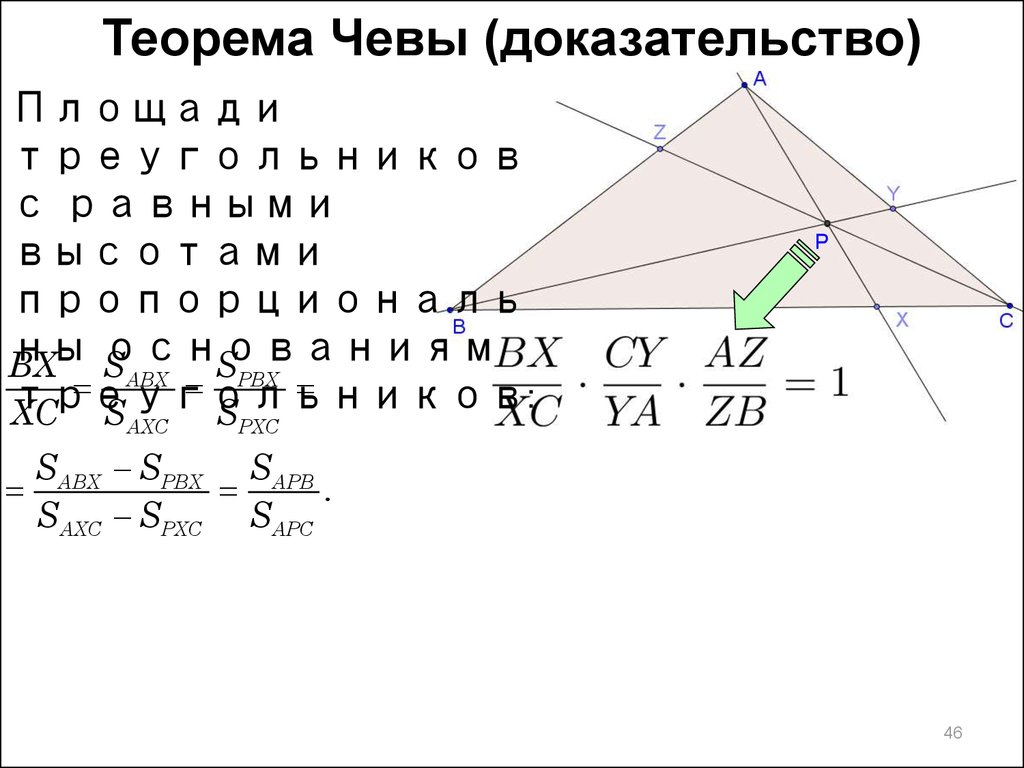
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
BX
SABX SPBX
треугольников:
XC S
S
AXC
P
PXC
SABX SPBX SAPB
.
SAXC SPXC SAPC
46
47.
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
BX
SABX SPBX
треугольников:
XC S
S
AXC
P
PXC
SABX SPBX SAPB
.
SAXC SPXC SAPC
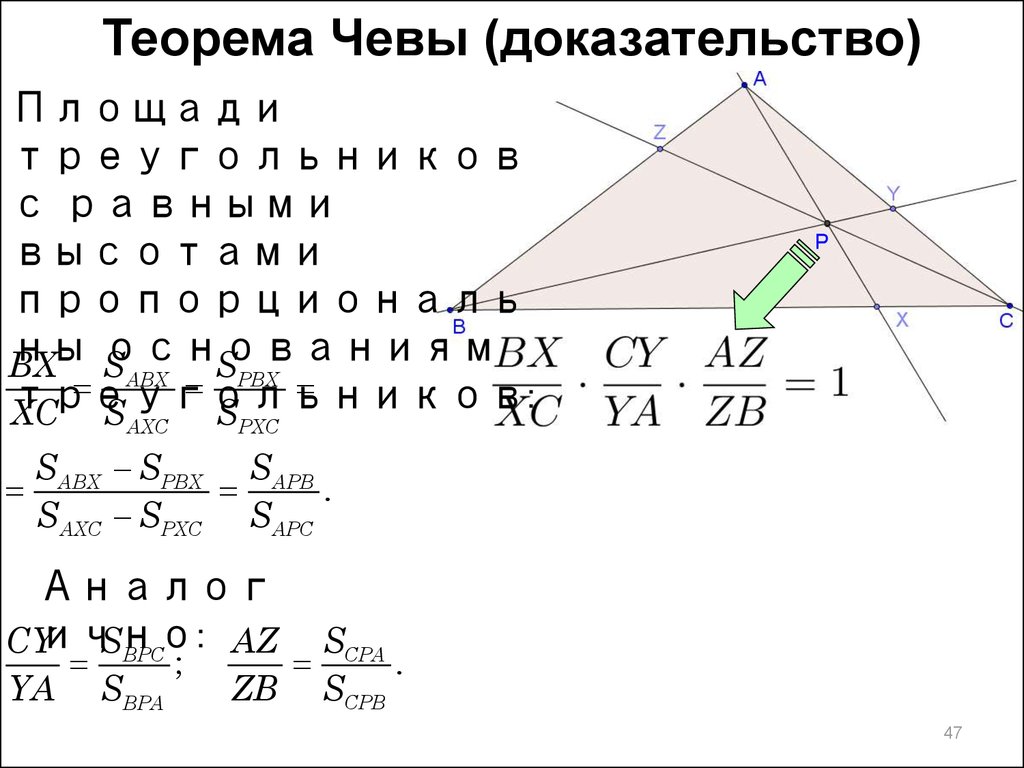
Аналог
SBPC
AZ
CYично:
YA
SBPA
;
SCPA
.
ZB SCPB
47
48.
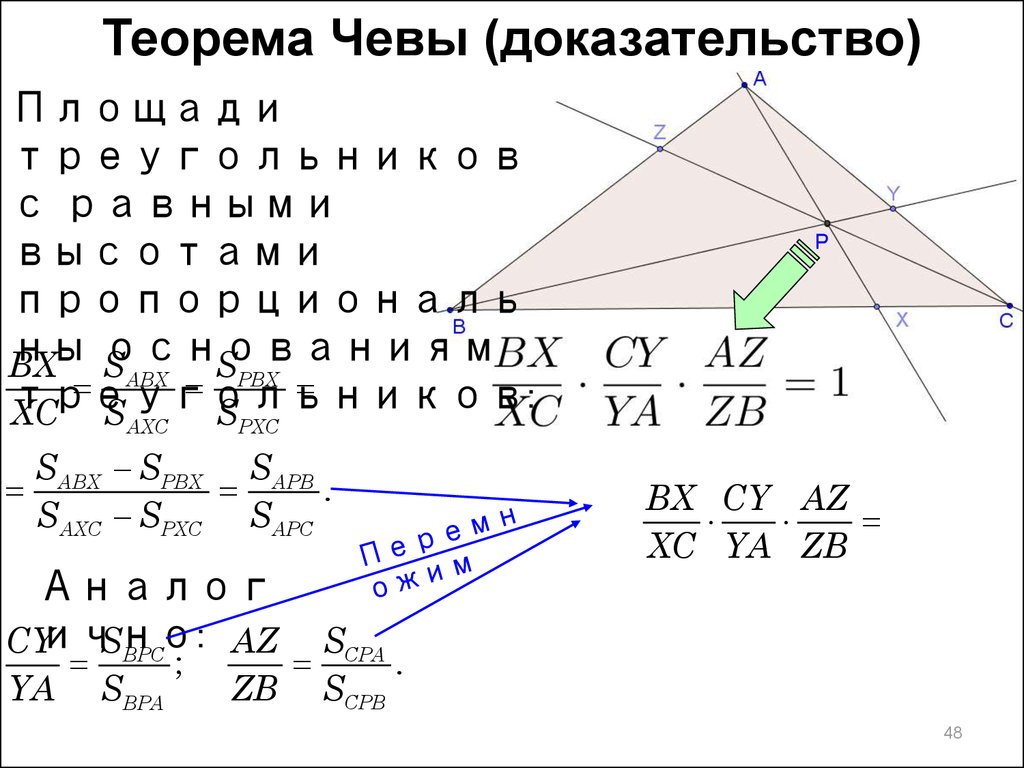
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
BX
SABX SPBX
треугольников:
XC S
S
AXC
P
PXC
SABX SPBX SAPB
.
SAXC SPXC SAPC
BX CY AZ
XC YA ZB
Аналог
SBPC
AZ
CYично:
YA
SBPA
;
SCPA
.
ZB SCPB
48
49.
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
BX
SABX SPBX
треугольников:
XC S
S
AXC
PXC
SABX SPBX SAPB
.
SAXC SPXC SAPC
Аналог
SBPC
AZ
CYично:
YA
SBPA
P
;
SCPA
.
ZB SCPB
BX CY AZ
XC YA ZB
SAPB SBPC SCPA
SAPC SBPA SCPB
49
50.
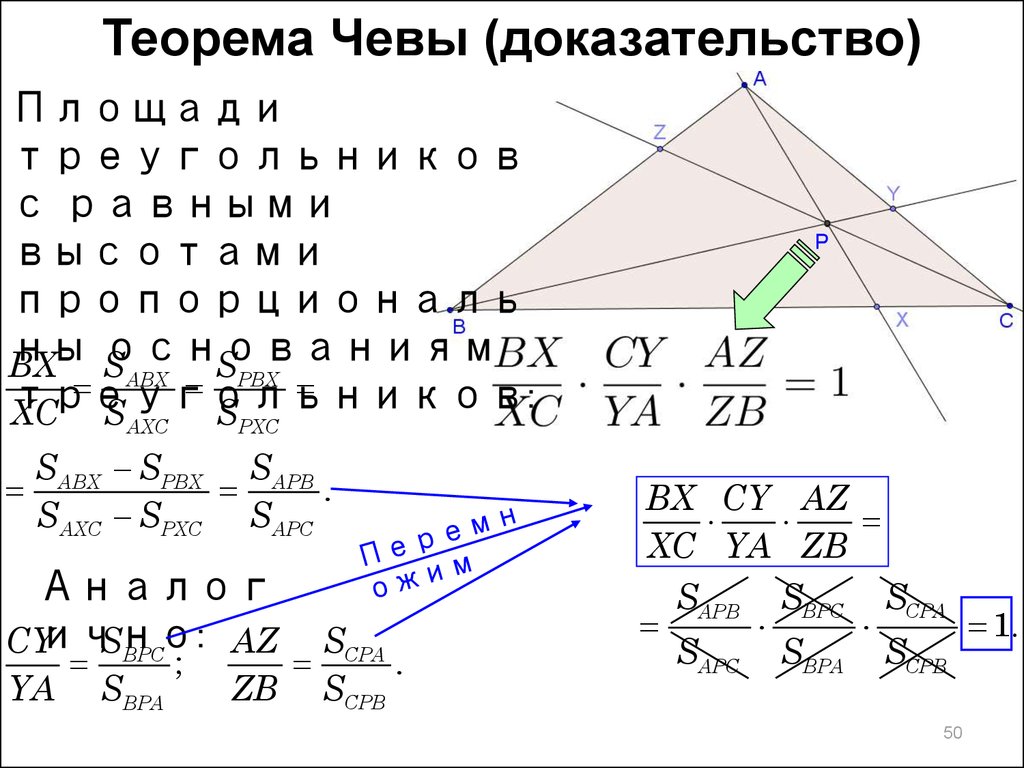
Теорема Чевы (доказательство)Площади
треугольников
с равными
высотами
пропорциональ
ны основаниям
BX
SABX SPBX
треугольников:
XC S
S
AXC
PXC
SABX SPBX SAPB
.
SAXC SPXC SAPC
Аналог
SBPC
AZ
CYично:
YA
SBPA
P
;
SCPA
.
ZB SCPB
BX CY AZ
XC YA ZB
SAPB
SAPC
SBPC
SBPA
SCPA
SCPB
50
1.
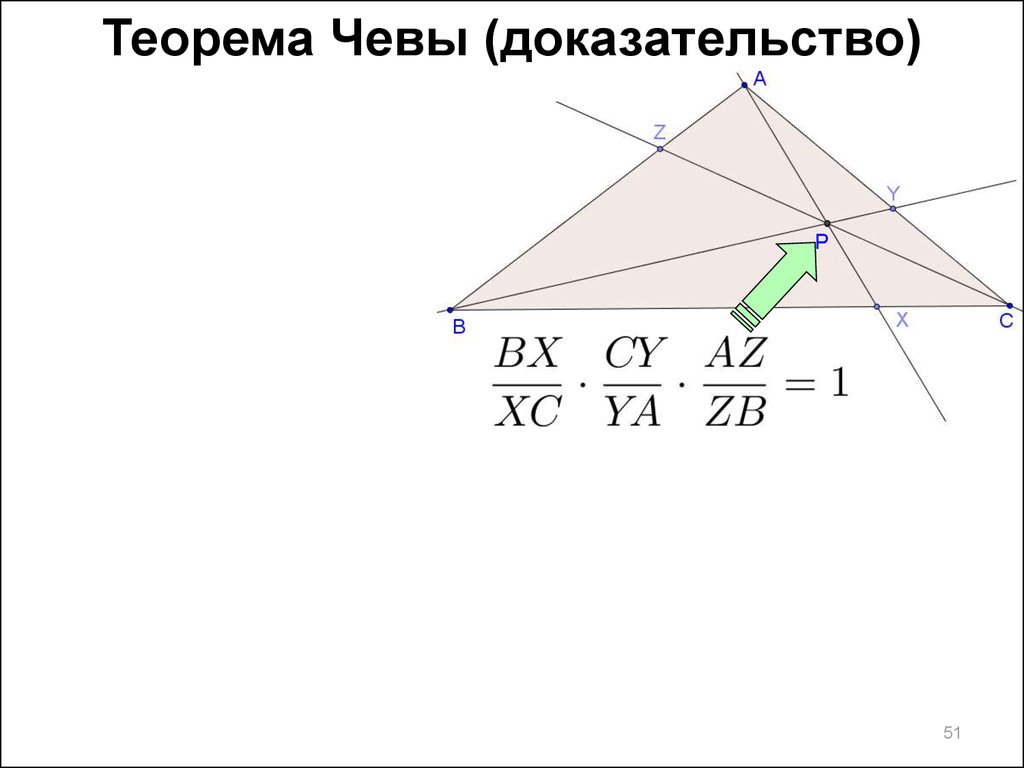
51.
Теорема Чевы (доказательство)P
51
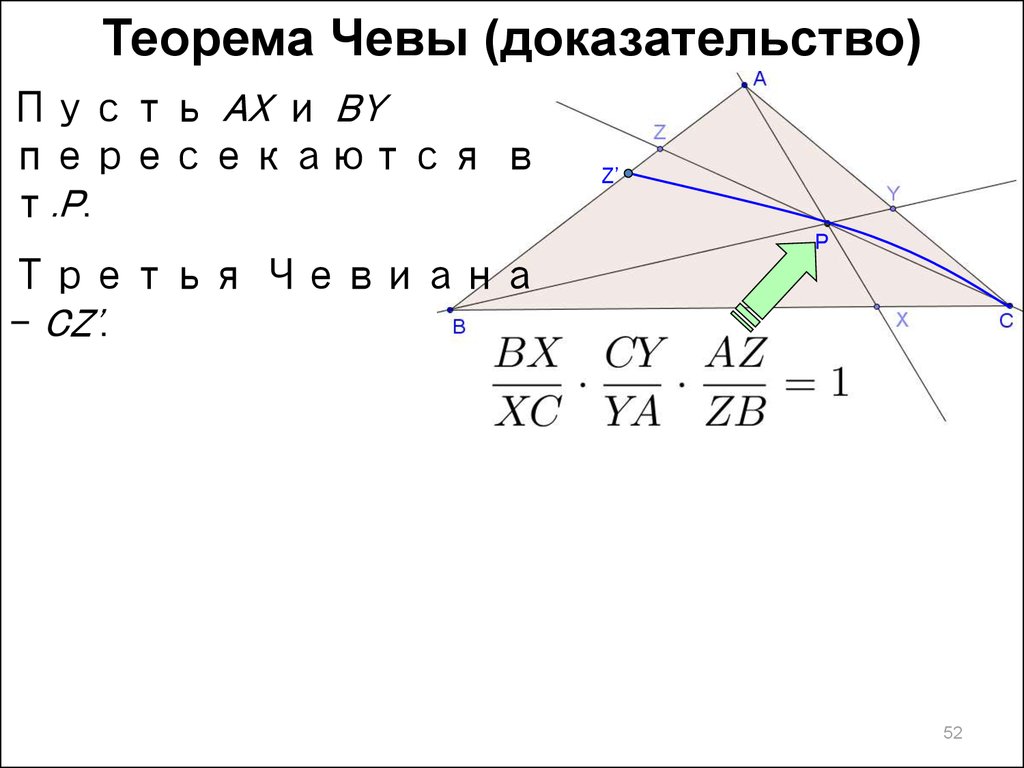
52.
Теорема Чевы (доказательство)Пусть AX и BY
пересекаются в
т.P.
Z'
P
Третья Чевиана
– CZ'.
52
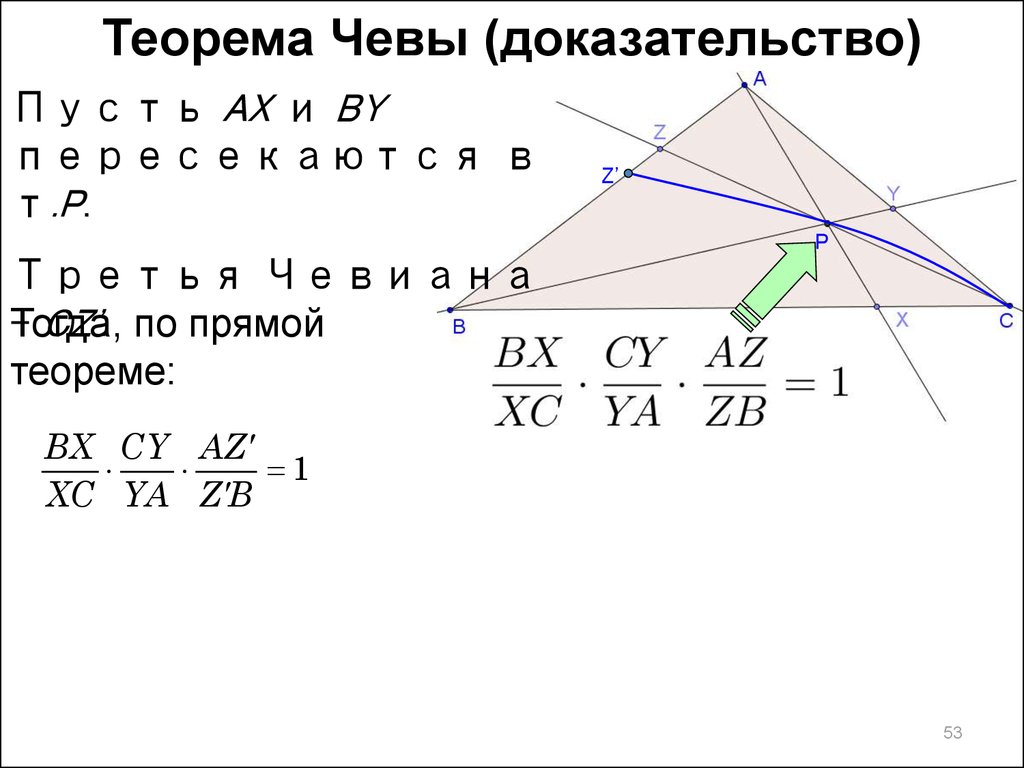
53.
Теорема Чевы (доказательство)Пусть AX и BY
пересекаются в
т.P.
Z'
P
Третья Чевиана
– CZ'. по прямой
Тогда,
теореме:
BX CY AZ
1
XC YA Z B
53
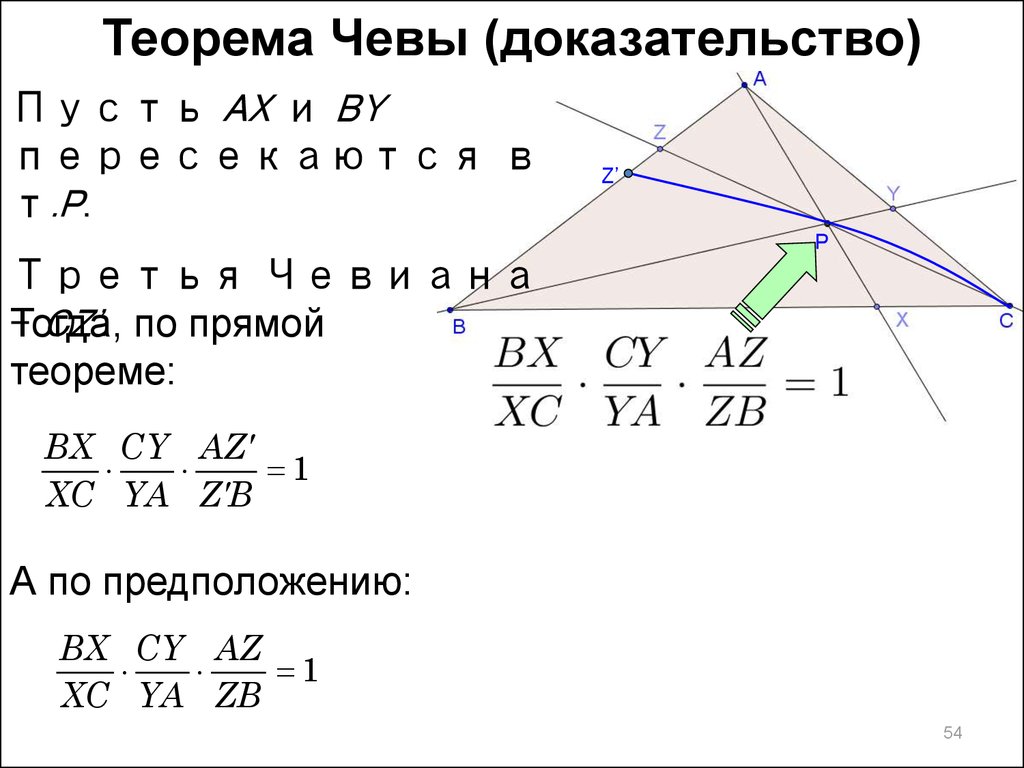
54.
Теорема Чевы (доказательство)Пусть AX и BY
пересекаются в
т.P.
Z'
P
Третья Чевиана
– CZ'. по прямой
Тогда,
теореме:
BX CY AZ
1
XC YA Z B
А по предположению:
BX CY AZ
1
XC YA ZB
54
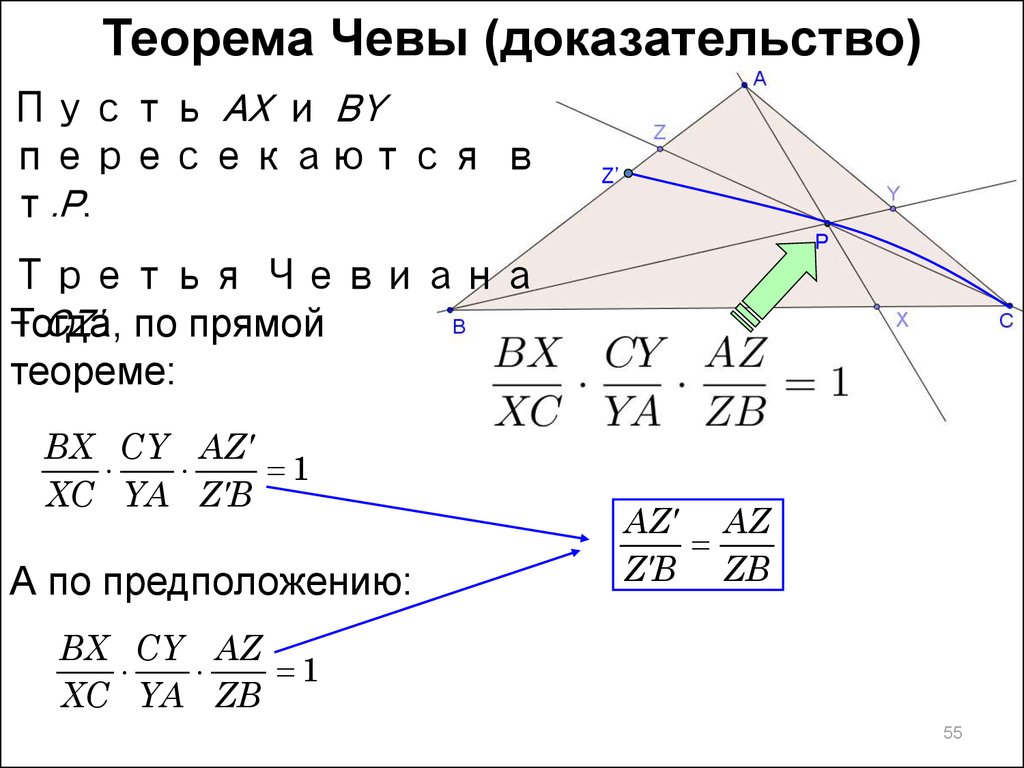
55.
Теорема Чевы (доказательство)Пусть AX и BY
пересекаются в
т.P.
Z'
P
Третья Чевиана
– CZ'. по прямой
Тогда,
теореме:
BX CY AZ
1
XC YA Z B
А по предположению:
AZ AZ
Z B ZB
BX CY AZ
1
XC YA ZB
55
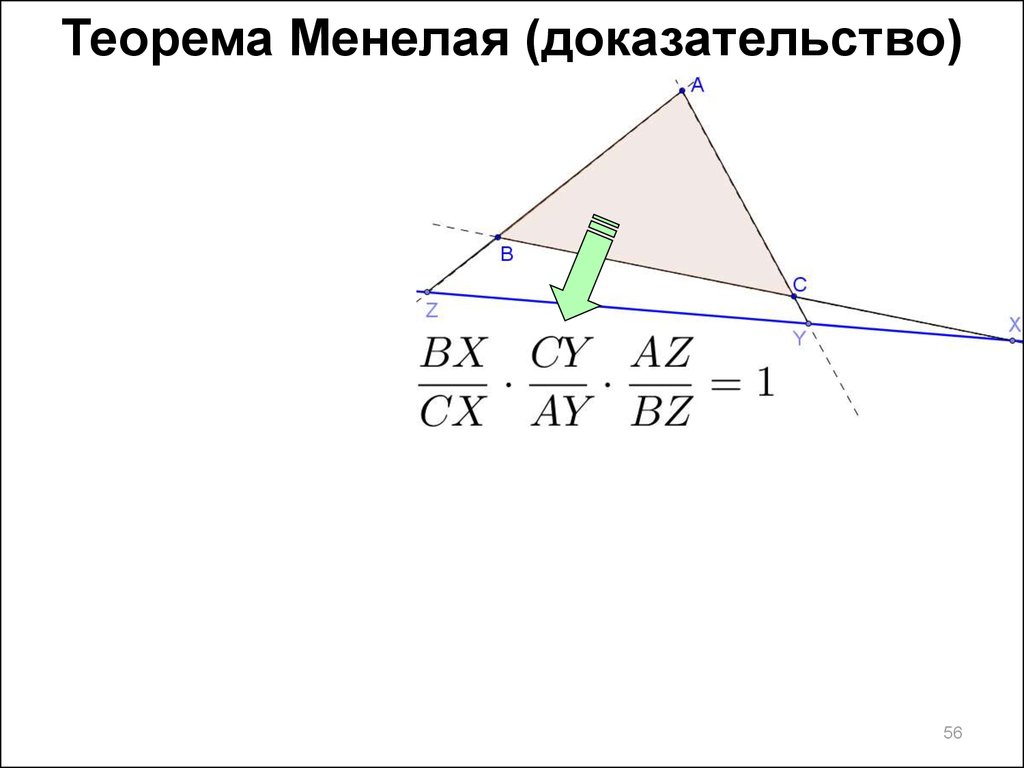
56.
Теорема Менелая (доказательство)56
57.
Теорема Менелая (доказательство)h1
h2
h3
57
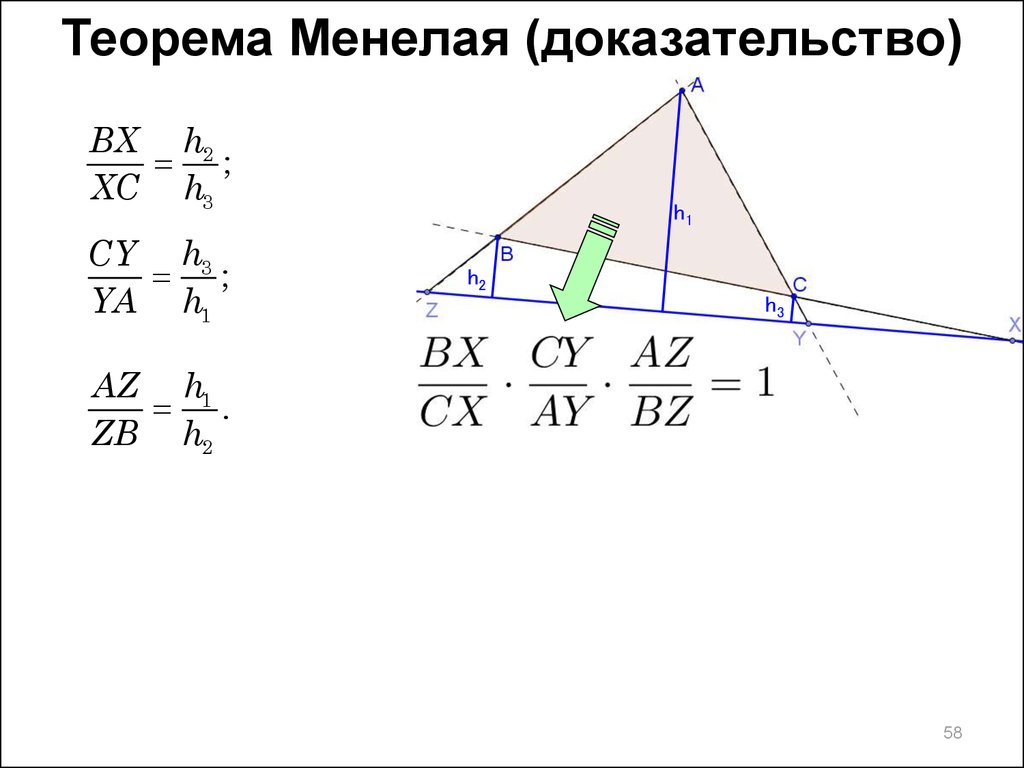
58.
Теорема Менелая (доказательство)BX h2
;
XC h3
CY h3
;
YA h1
h1
h2
h3
AZ h1
.
ZB h2
58
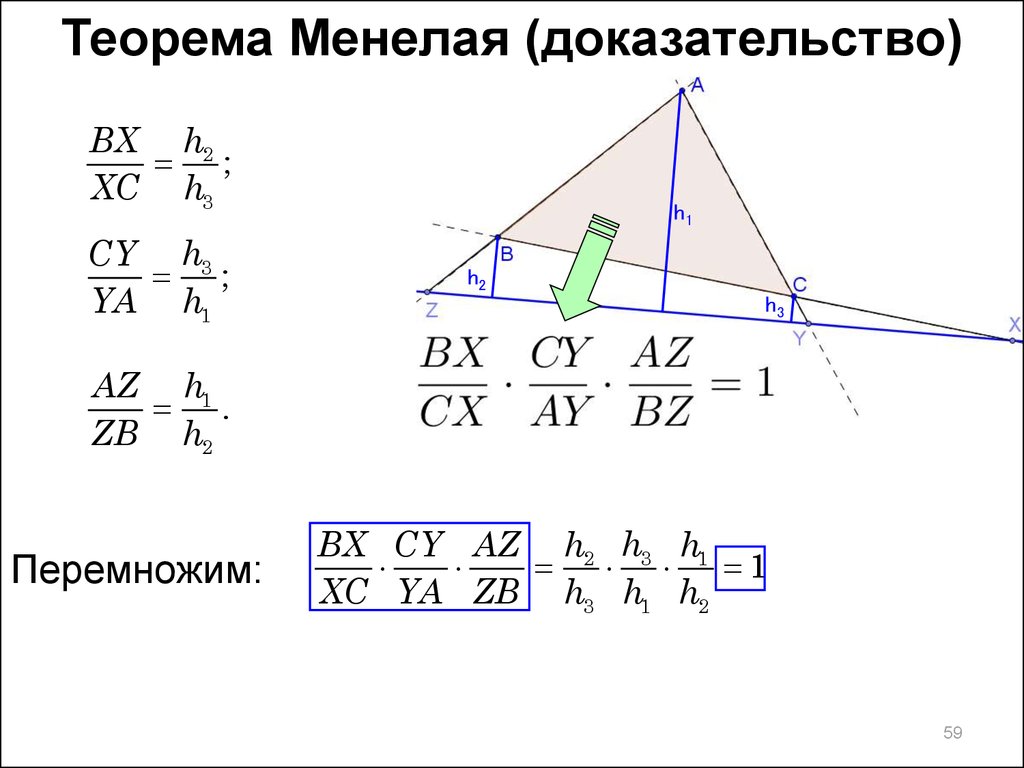
59.
Теорема Менелая (доказательство)BX h2
;
XC h3
CY h3
;
YA h1
h1
h2
h3
AZ h1
.
ZB h2
Перемножим:
BX CY AZ h2 h3 h1
1
XC YA ZB h3 h1 h2
59
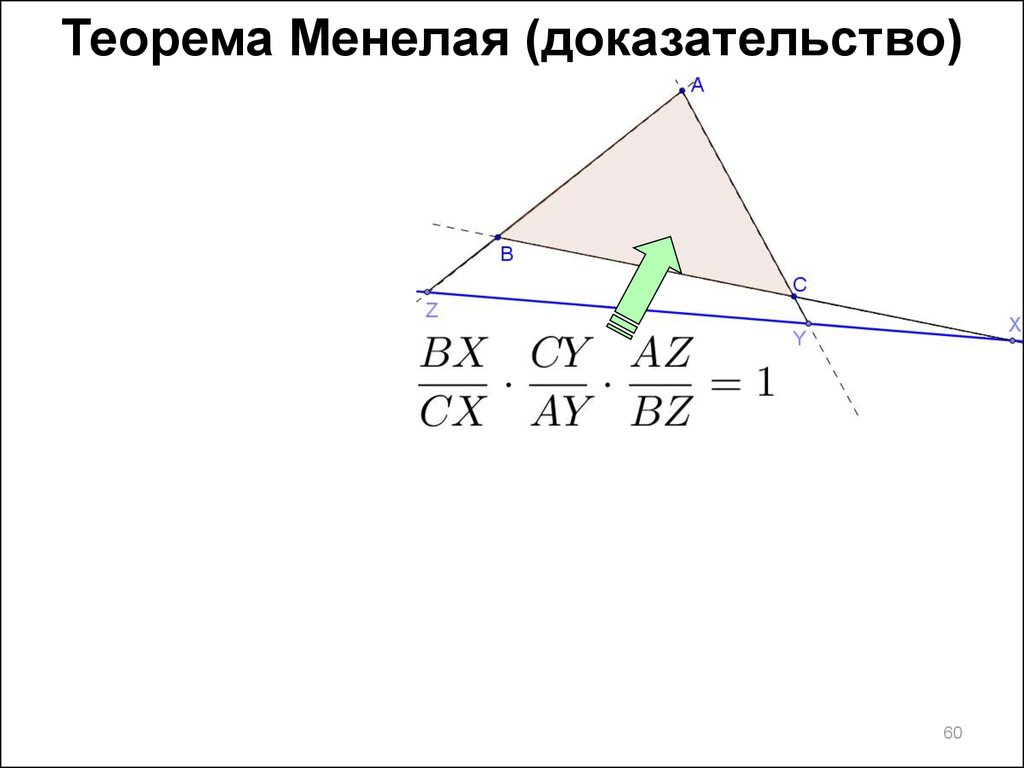
60.
Теорема Менелая (доказательство)60
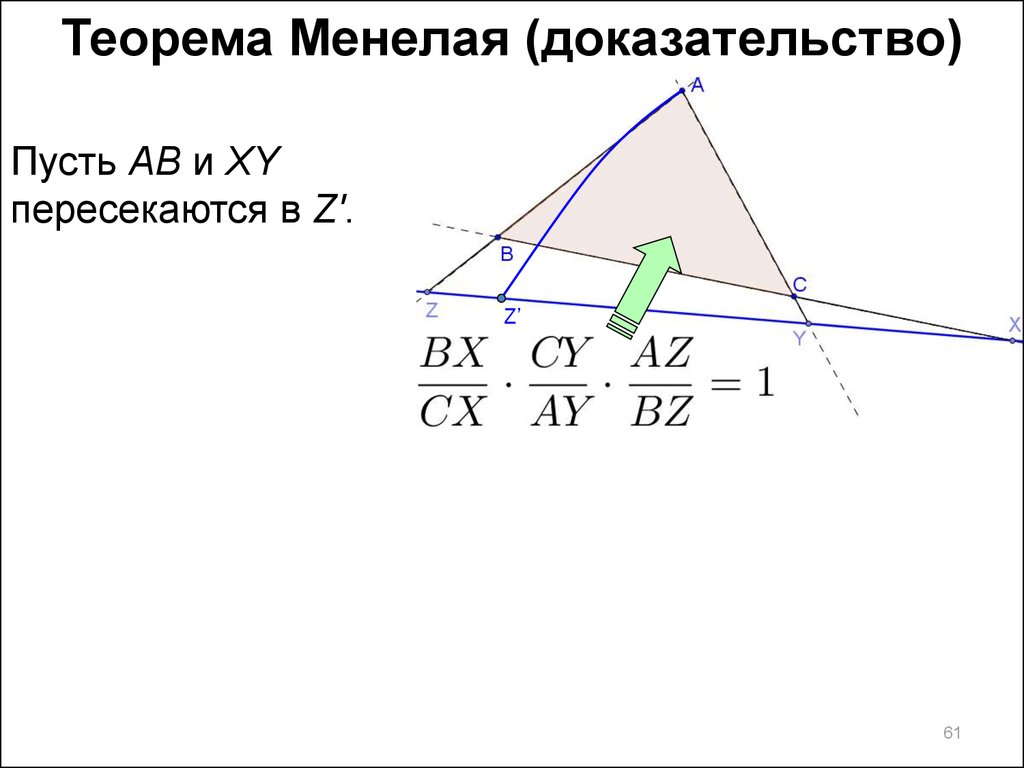
61.
Теорема Менелая (доказательство)Пусть AB и XY
пересекаются в Z'.
Z'
61
62.
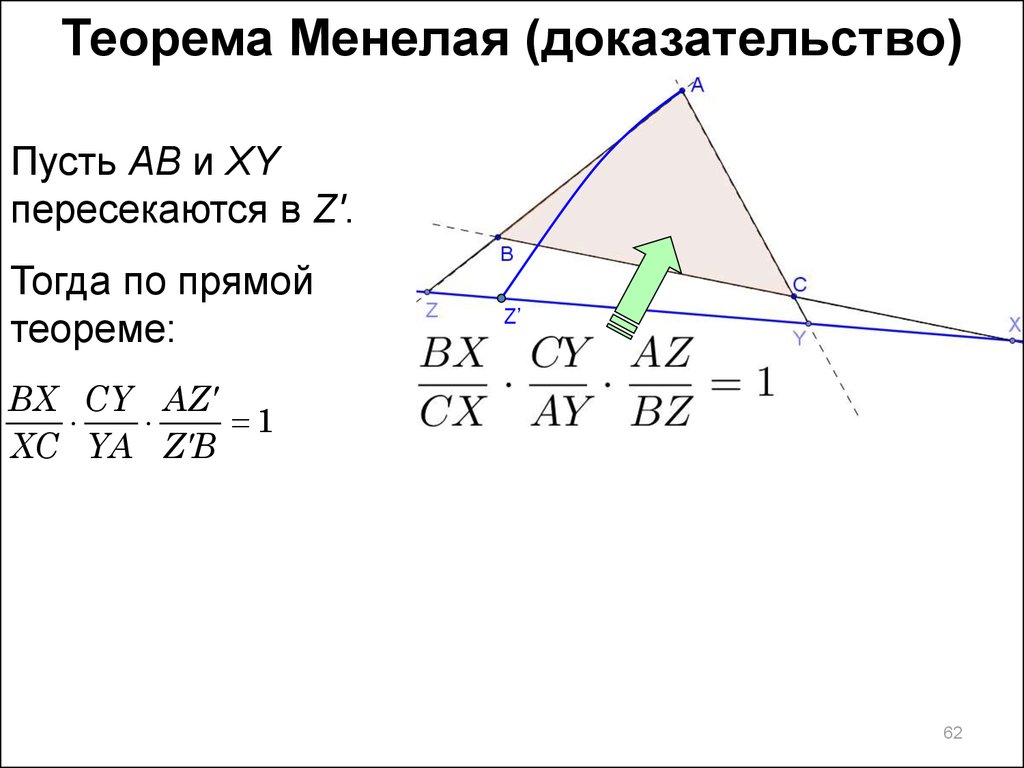
Теорема Менелая (доказательство)Пусть AB и XY
пересекаются в Z'.
Тогда по прямой
теореме:
Z'
BX CY AZ
1
XC YA Z B
62
63.
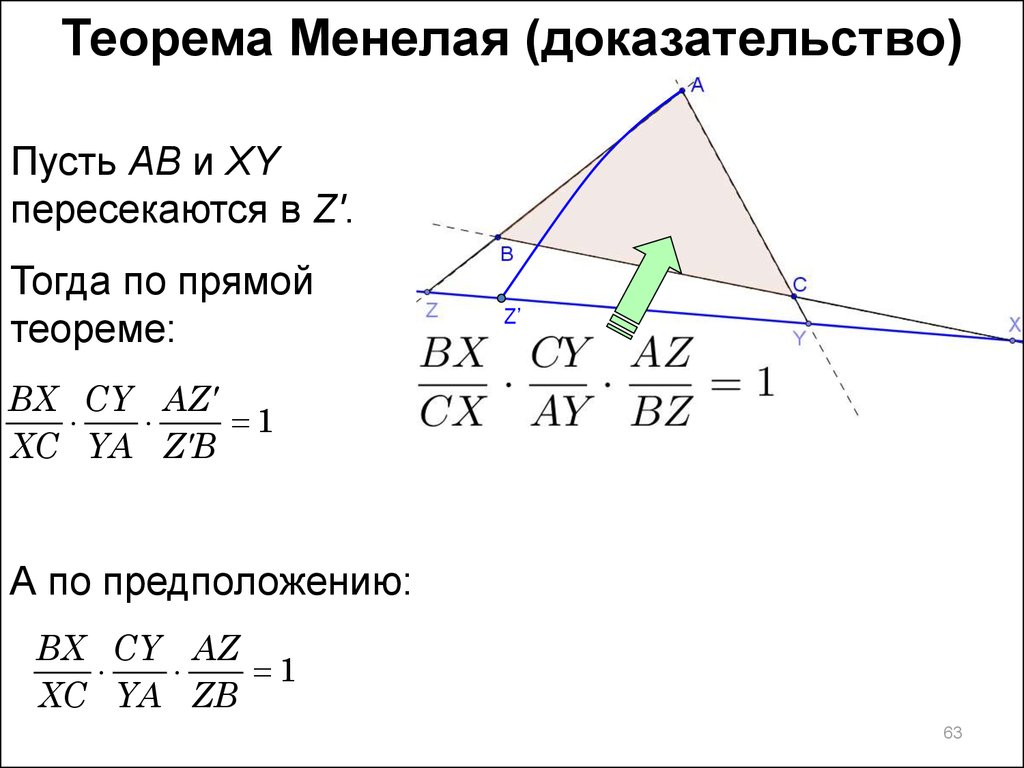
Теорема Менелая (доказательство)Пусть AB и XY
пересекаются в Z'.
Тогда по прямой
теореме:
Z'
BX CY AZ
1
XC YA Z B
А по предположению:
BX CY AZ
1
XC YA ZB
63
64.
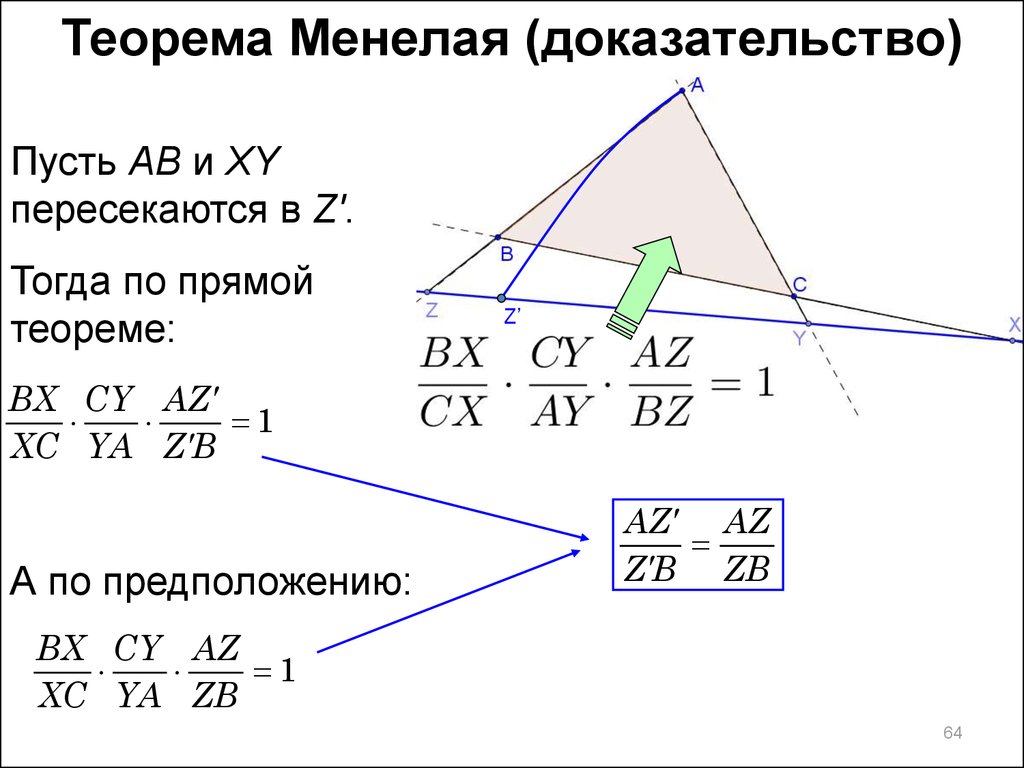
Теорема Менелая (доказательство)Пусть AB и XY
пересекаются в Z'.
Тогда по прямой
теореме:
Z'
BX CY AZ
1
XC YA Z B
А по предположению:
AZ AZ
Z B ZB
BX CY AZ
1
XC YA ZB
64

































 mathematics
mathematics








