Основы стереометрии

1. Основы стереометрии

1

2. Школьный курс геометрии состоит из двух частей:

•ПЛАНИМЕТРИИ
•СТЕРЕОМЕТРИИ
Планиметрия - это раздел
геометрии, в котором
изучаются свойства
геометрических фигур
на плоскости.
Стереометрия - это раздел
геометрии, в котором
изучаются свойства
геометрических фигур
в пространстве.
Слово «стереометрия» происходит от греческих
слов «стереос» - объемный, пространственный и
«метрео» - измерять.
2

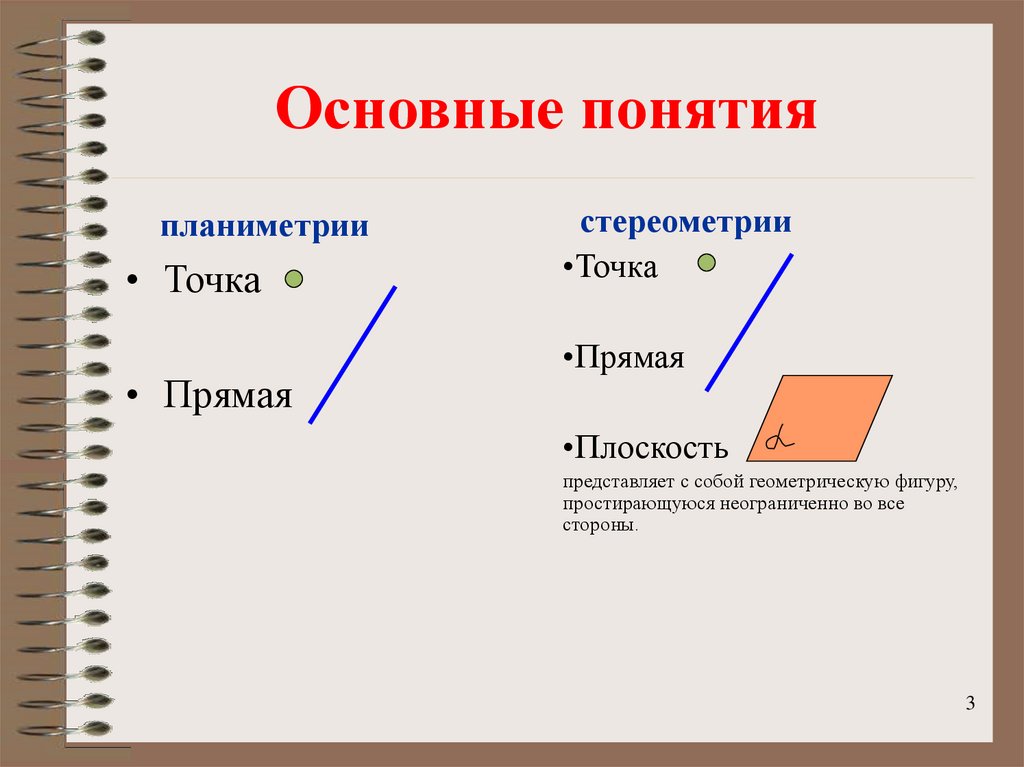
3. Основные понятия

планиметрии
• Точка
• Прямая
стереометрии
•Точка
•Прямая
•Плоскость
представляет с собой геометрическую фигуру,
простирающуюся неограниченно во все
стороны.
3

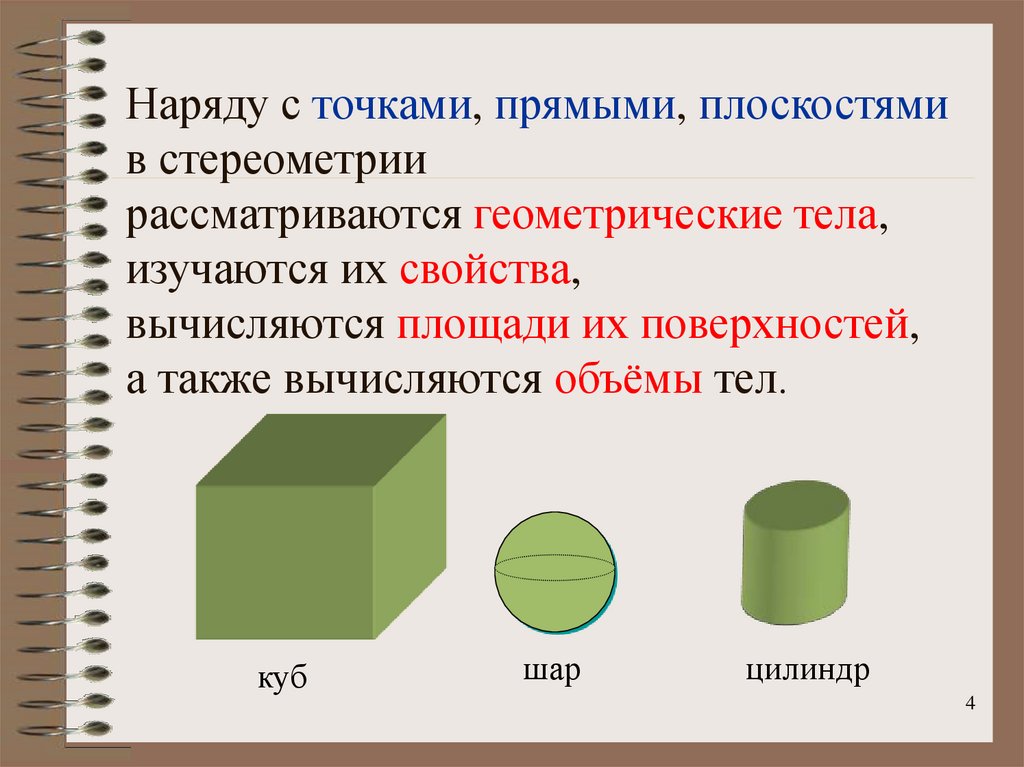
4. Наряду с точками, прямыми, плоскостями в стереометрии рассматриваются геометрические тела, изучаются их свойства, вычисляются

площади их поверхностей,
а также вычисляются объёмы тел.
куб
шар
цилиндр
4

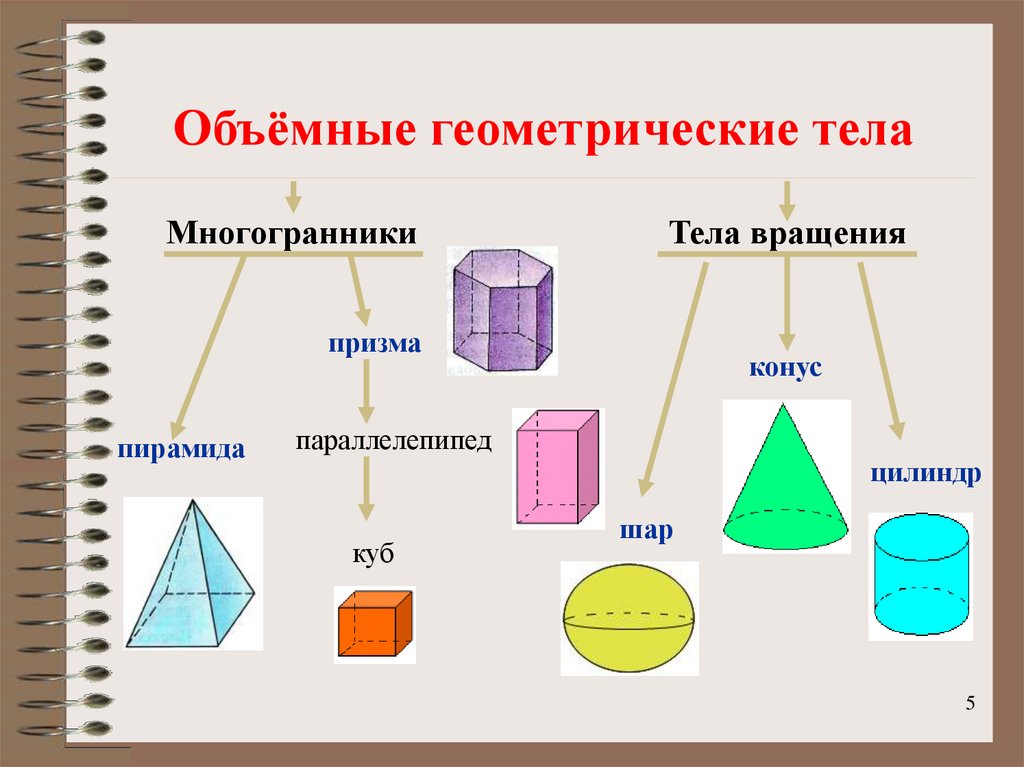
5. Объёмные геометрические тела

Многогранники
Тела вращения
призма
пирамида
конус
параллелепипед
цилиндр
куб
шар
5

6. Точки обозначаются прописными латинскими буквами А, В, С, D, Е, К,…

А
В
С
Е
Прямые обозначаются строчными
латинскими буквами a, b, c, d, e, k,…
b
d
a
Плоскости обозначаются греческими
буквами α, β, γ, λ, π, ω,…
β
γ
α
6

7. Стереометрия широко используется в строительном деле

7

8. Стереометрия используется в архитектуре

8

9. Стереометрия используется в машиностроении

9

10. Стереометрия используется в геодезии

Геодезия - наука, занимающаяся изучением вида и
размера Земли.
Во многих других областях науки и техники.
10

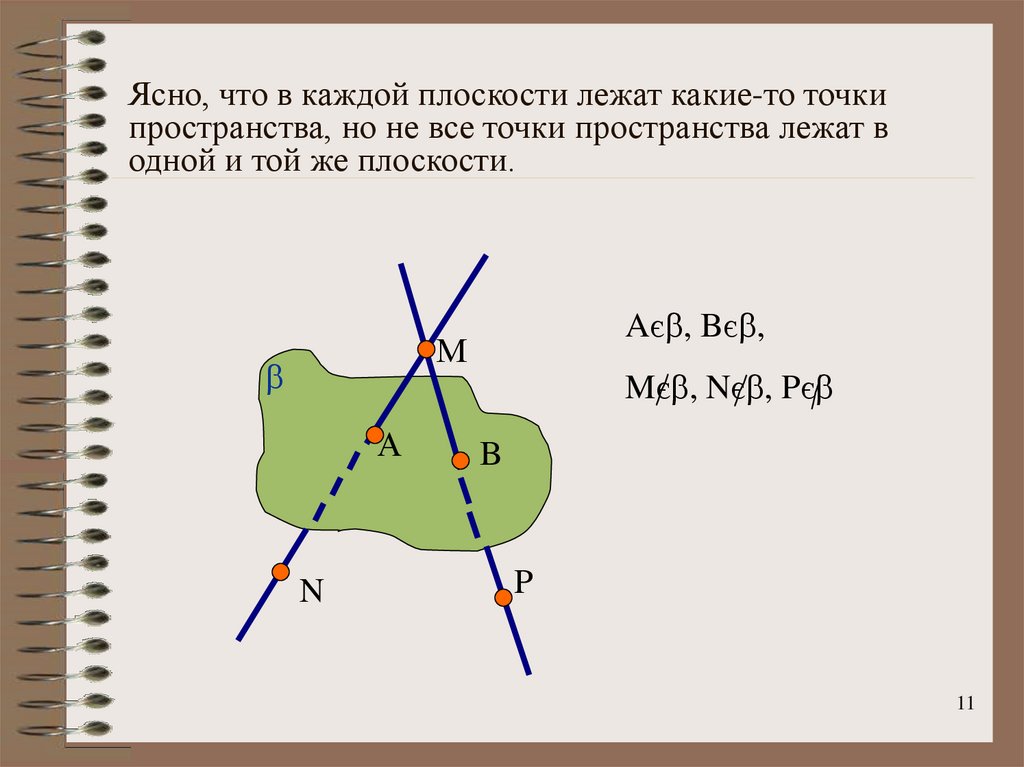
11. Ясно, что в каждой плоскости лежат какие-то точки пространства, но не все точки пространства лежат в одной и той же плоскости.

Aє , Bє ,
М
Mє , Nє , Pє
А
N
B
P
11

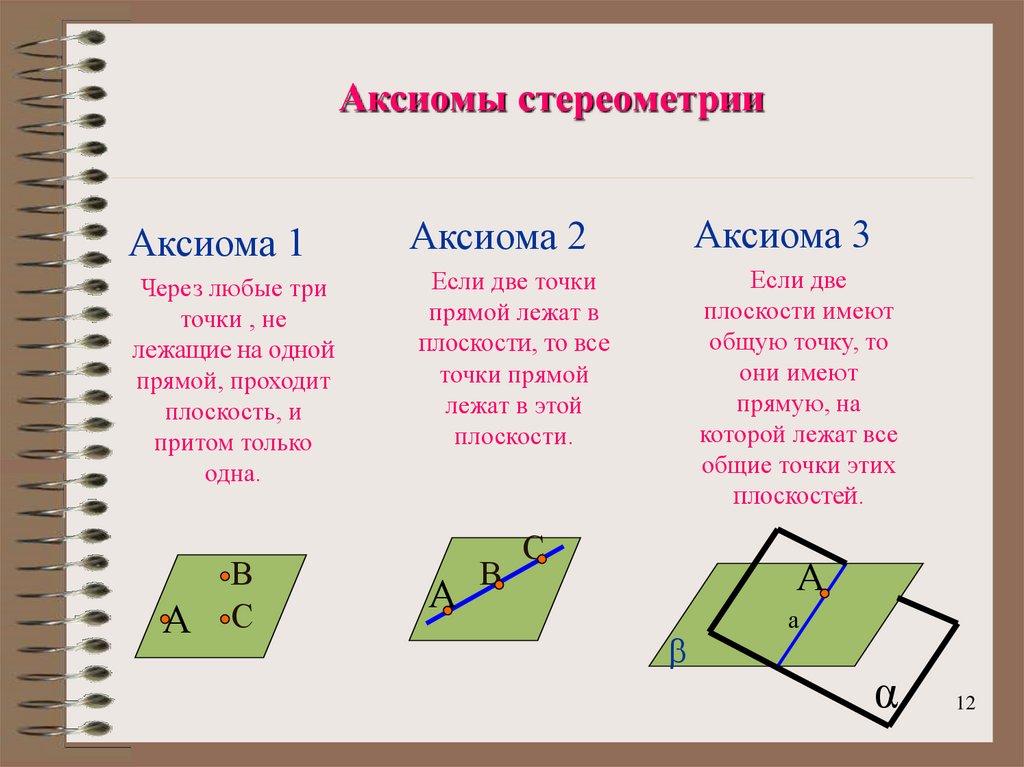
12. Аксиомы стереометрии

Аксиома 1
Через любые три
точки , не
лежащие на одной
прямой, проходит
плоскость, и
притом только
одна.
А
В
С
Аксиома 3
Аксиома 2
Если две
плоскости имеют
общую точку, то
они имеют
прямую, на
которой лежат все
общие точки этих
плоскостей.
Если две точки
прямой лежат в
плоскости, то все
точки прямой
лежат в этой
плоскости.
А
В
С
А
а
α
12

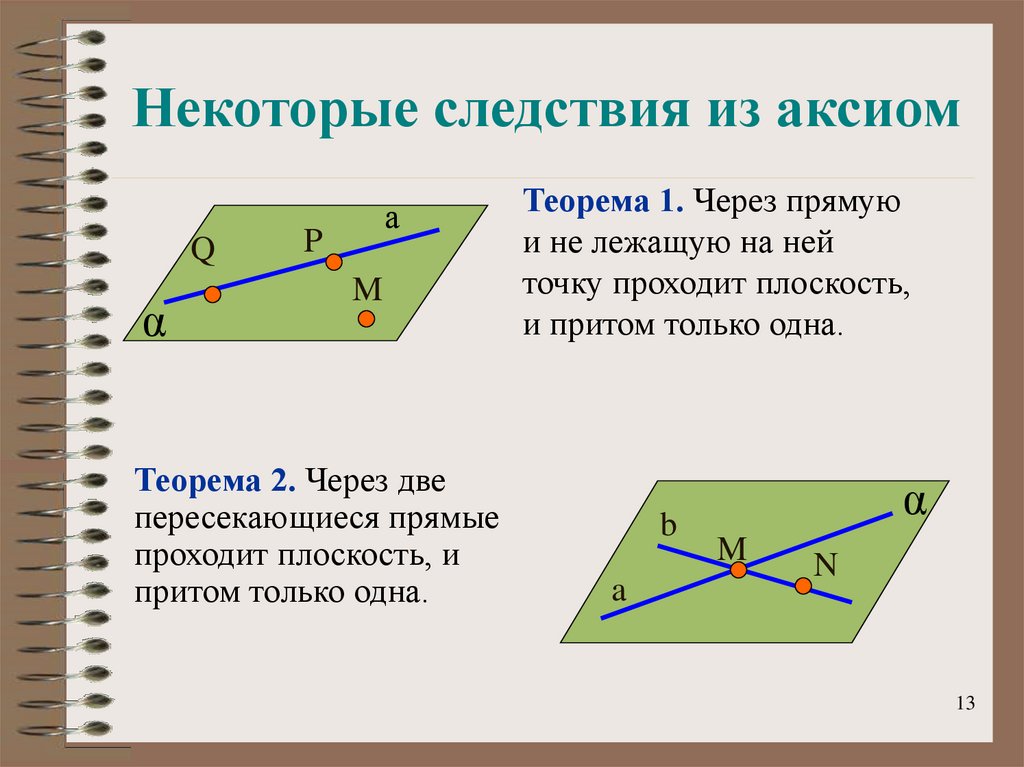
13. Некоторые следствия из аксиом

Q
α
а
P
M
Теорема 2. Через две
пересекающиеся прямые
проходит плоскость, и
притом только одна.
Теорема 1. Через прямую
и не лежащую на ней
точку проходит плоскость,
и притом только одна.
b
a
α
M
N
13