Вычисление площадей фигур на клетчатой бумаге. Формула Пика (8 класс)

1.

Вычисление площадей фигур
на клетчатой бумаге.
Формула Пика.

2.

Подумай
Площадь прямоугольника
S=½*a*h
Верно
S=a*b Подумай
S=½*a*b
Подумай
S=a*h
a
b

3.

Подумай
Площадь параллелограмма
S=½*a*h
Подумай
S=a*b Подумай
S=½*a*b
Верно
S=a*h
h
a

4.

Подумай
Площадь треугольника
S=a*h
Подумай
h
S=a*b
Верно
S=½*a*h
Подумай
S=½*d1*d2
a

5.

Верно
S=½*a*b
Подумай
S=a*b
Подумай
S= (a+b) *h
2 Подумай
S=½*d1*d2
Площадь прямоугольного
треугольника
a
b

6.

Подумай
Площадь ромба
S= (a+b) *h
2 Подумай
S=a*b
Верно
S=½*d1*d2
Подумай
S=½*a*b
d1
d2

7.

Подумай
Площадь трапеции
a
S=½*d1*d2
Подумай
S=a*b
Подумай
S=½*a*b
Верно
S= (a+b) *h
2
h
b

8.

Найдите площади фигур, изображённых на клетчатой бумаге с
размером клетки 1см*1см. Ответ дайте в квадратных сантиметрах.
S=½*2*9=9 см2
S=½*2*6=6 см2
S=½*3*8=12 см2
S=½*2*6=6 см2
S=½*(2+5)*4=14 см2 S=3*4=12 см2

9.

S1=½*(4+1)*3=7,5 см2
s2 S =½*(2+6)*3=12 см
s1
2
S3=4*3=12 см2
S4=½*4*2=4 см2
s3
s4
2

10.

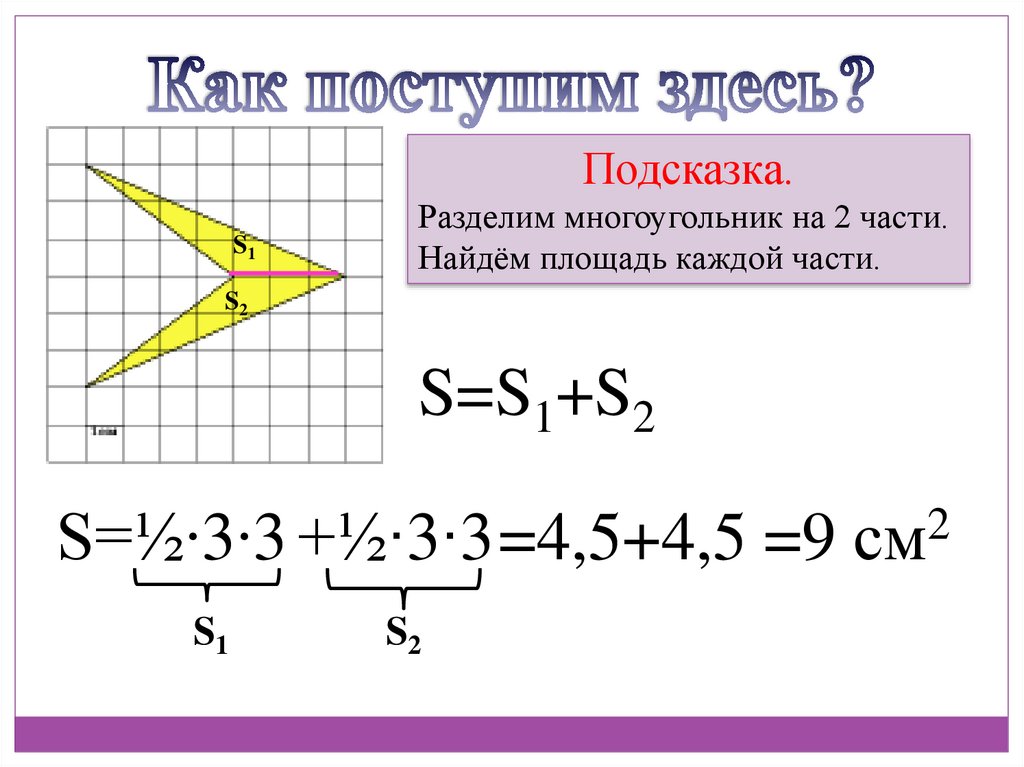
Подсказка.
S1
Разделим многоугольник на 2 части.
Найдём площадь каждой части.
S2
S=S1+S2
2
S=½∙3∙3 +½∙3∙3 =4,5+4,5 =9 см
S1
S2

11.

Подсказка.
S3
S2
Разделим многоугольник на части.
Найдём площадь каждой части.
S1
S=S1+S2
S=S1+S2+S3
2
S=½∙1∙2+½∙1∙4
=1+2
=3
см
S=½∙1∙1+½∙1∙3+1∙1 =0,5+1,5+1=
S1
=3 см2
S2
S3
Или так

12.

Подсказка.
Достроим до квадрата.
S1
S
S3
S2
S=Sкв-S1-S2-S3
S=4∙4 -½∙4∙2 -½∙3∙2 -½∙1∙4=
SКВ
S1
S2
=16-4-3-2 =7 см2
S3

13.

S1
Подсказка.
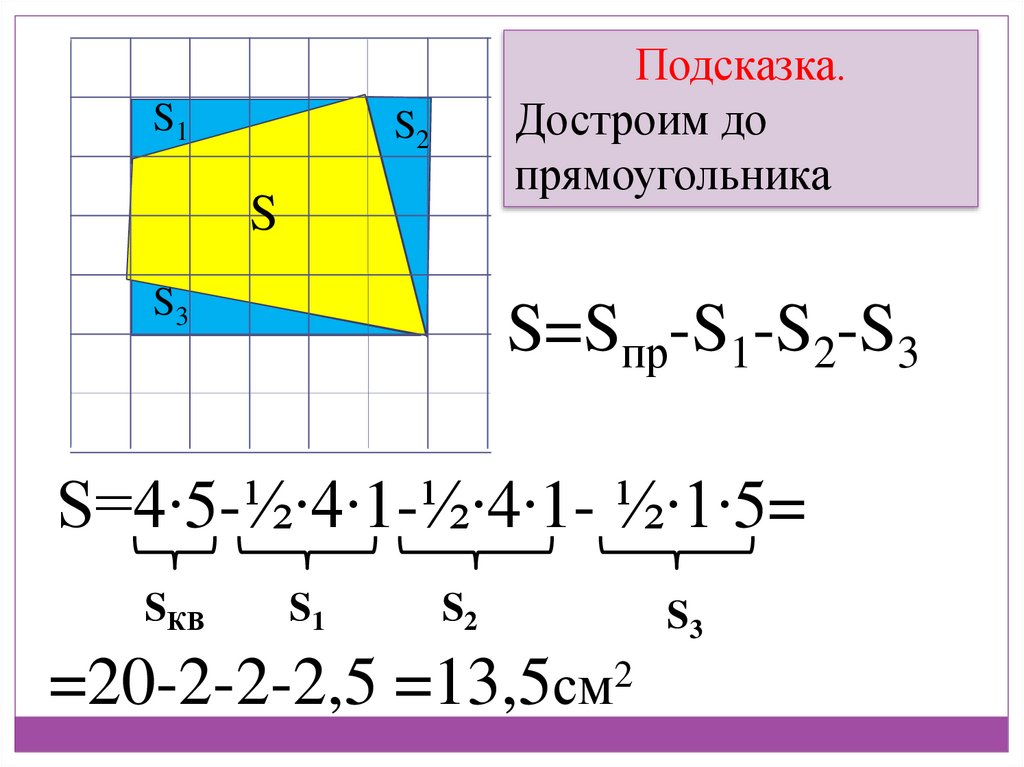
Достроим до
прямоугольника
S2
S
S3
S=Sпр-S1-S2-S3
S=4∙5-½∙4∙1-½∙4∙1- ½∙1∙5=
SКВ
S1
S2
=20-2-2-2,5 =13,5см2
S3

14.

S5 S 1
S4
S2
S
S=Sкв-S1-S2-S3-S4
S3
S=5∙5-½∙3∙1-½∙5∙1- ½∙2∙5 - ½∙1∙2-1∙1=
SКВ
S1
S2
S3
=25-1,5-2,5-5-1-1 =13,5см2
S4
S5

15.

Позволит вам с необычайной легкостью
находить площадь любого многоугольника на
клетчатой бумаге с целочисленными вершинами.
Формула Пика очень удобна когда сложно
догадаться, как разбить фигуру на удобные
многоугольники
или
достроить
до
прямоугольника, квадрата …

16.

Георг Александр Пик— австрийский
математик.
Дата рождения:
10 августа 1859
Место рождения:
Вена
Дата смерти:
13 июля 1942 (82 года)
Место смерти:
концлагерь
Терезиенштадт
Научная сфера:
математика
Место работы:
Немецкий университет в
Праге
Учёная степень:
доктор философии (PhD)
по математике,
Учёное звание:
профессор

17.

Определение: Точка координатной
плоскости называется целочисленной, если обе
её координаты целые числа.
Площадь многоугольника с
целочисленными вершинами равна
Г
B+ – 1
2
где
В — количество целочисленных точек внутри
многоугольника, а
Г — количество целочисленных точек на
границе многоугольника.

18.

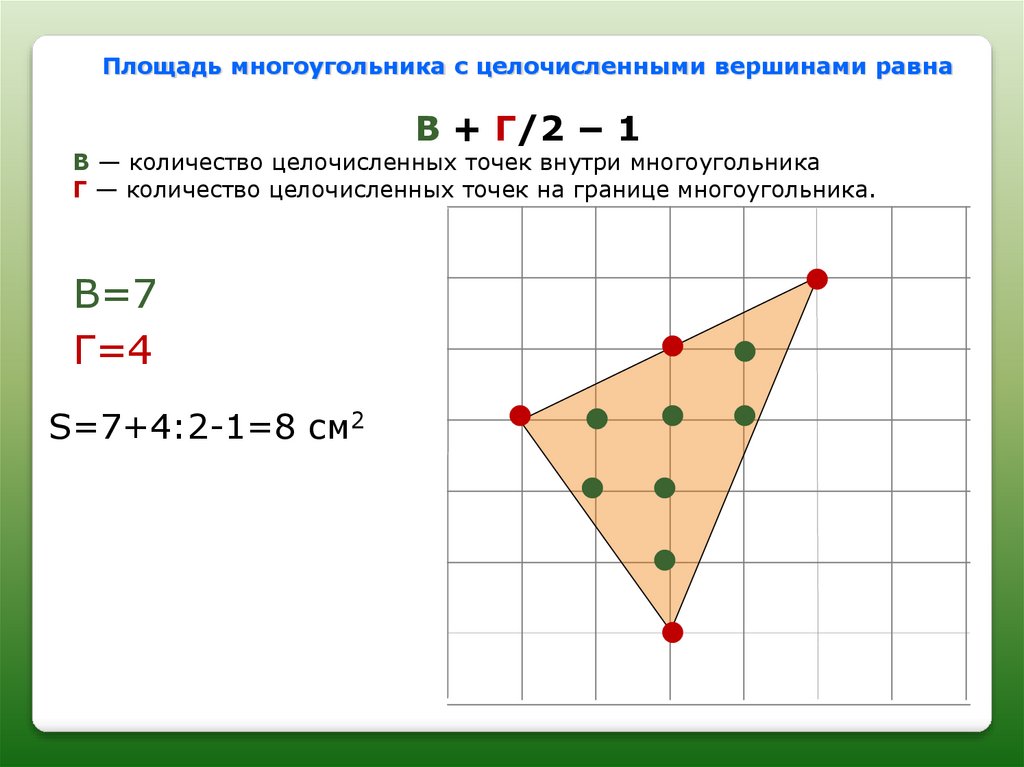
Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В — количество целочисленных точек внутри многоугольника
Г — количество целочисленных точек на границе многоугольника.
В=10
Г=7
S=10+7:2-1=12,5 см2

19.

Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В — количество целочисленных точек внутри многоугольника
Г — количество целочисленных точек на границе многоугольника.
В=11
Г=9
S=11+9:2-1=14,5 см2

20.

Площадь многоугольника с целочисленными вершинами равна
В + Г/2 − 1
В — количество целочисленных точек внутри многоугольника
Г — количество целочисленных точек на границе многоугольника.
В=7
Г=4
S=7+4:2-1=8 см2

21.

1 способ:
В=8
Г=7
S=8+7:2-1=10,5 см2
2 способ:
S=4∙5-½∙1∙1-½∙2∙3½∙3∙4=10,5 см2

22.

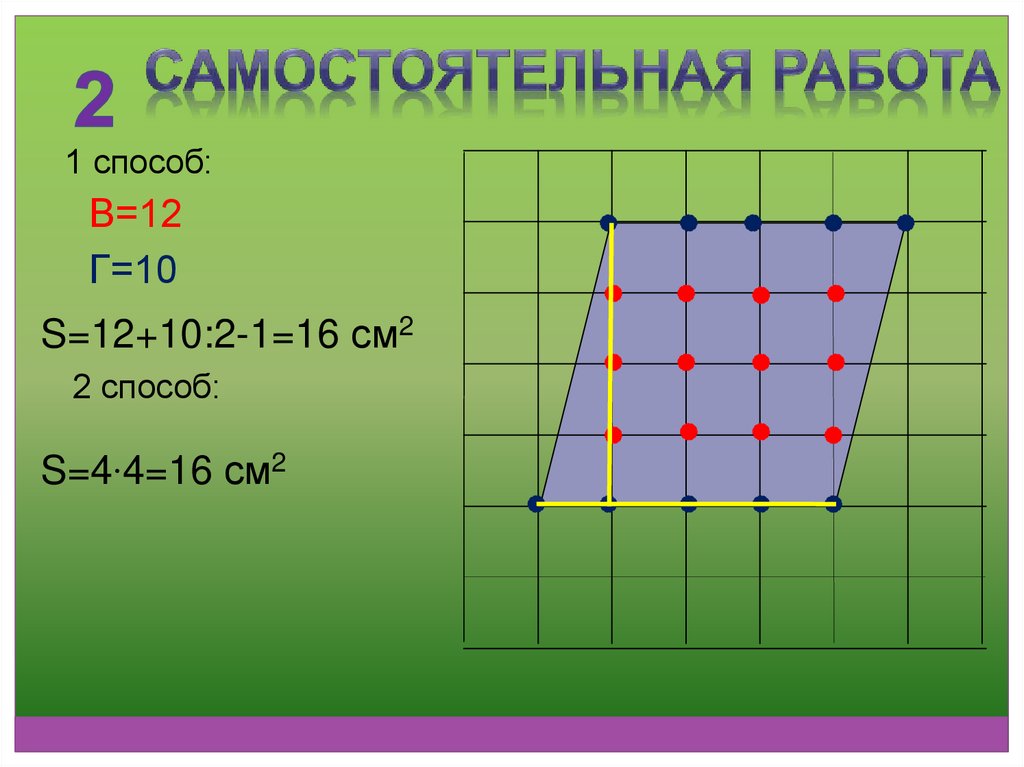
1 способ:
В=12
Г=10
S=12+10:2-1=16 см2
2 способ:
S=4∙4=16 см2

23.

1 способ:
В=0
Г=8
S=0+8:2-1=3 см2
2 способ:
S=(½∙1∙3)∙2=3 см2

24.

1 способ:
В=5
Г=4
S=5+4:2-1=6 см2
2 способ:
S=4∙5-½∙1∙3-½∙3∙5½∙2∙4=6 см2

25.

1 способ:
В=11
Г=4
S=11+4:2-1=12 см2
2 способ:
S=½∙4∙6=12 см2