Властивості функції: парні і непарні, зростання і спадання функції

1. Властивості функції: парні і непарні, зростання і спадання функції

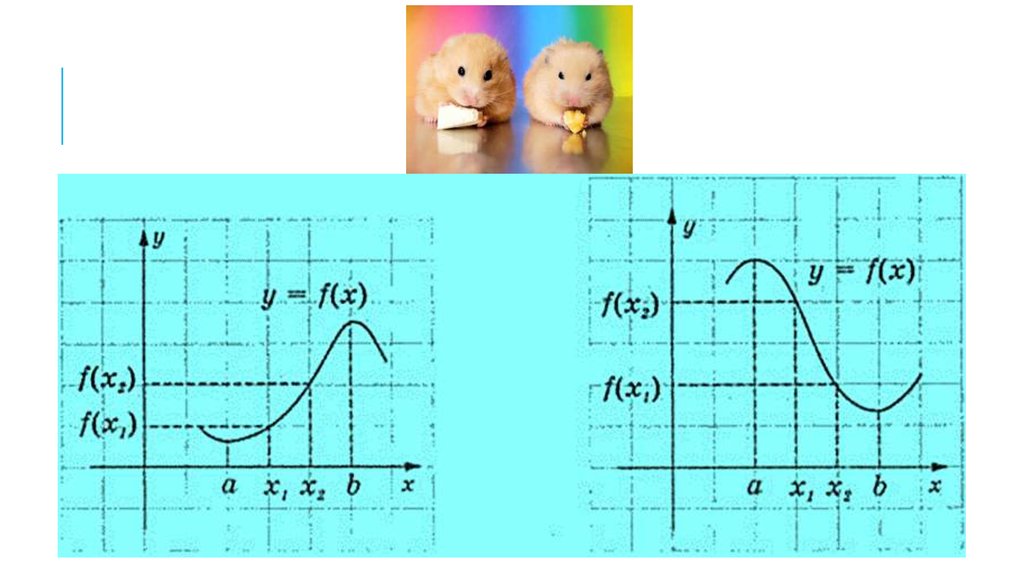
2. зростання і спадання функції

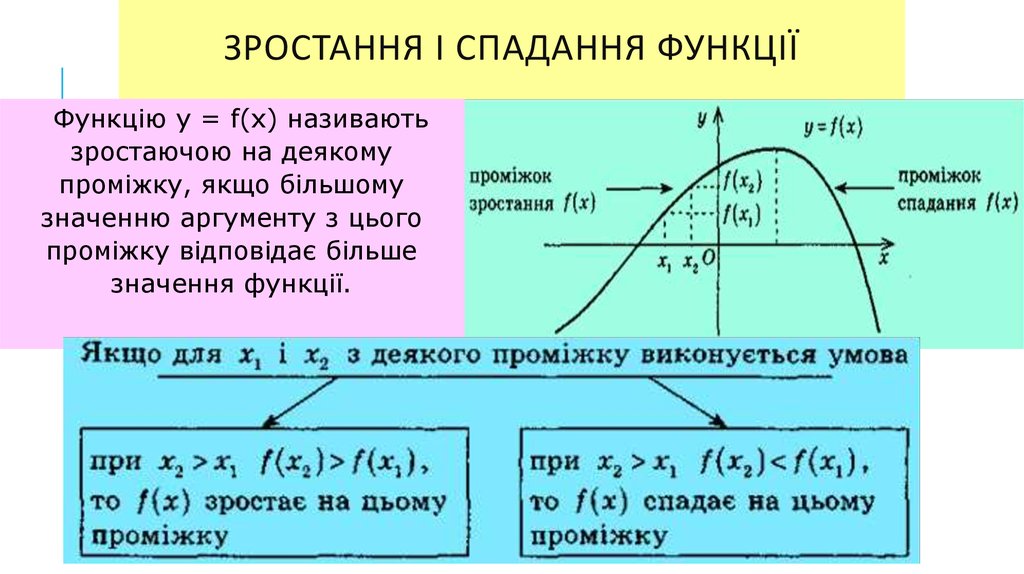
ЗРОСТАННЯ І СПАДАННЯ ФУНКЦІЇ
Функцію у = f(х) називають
зростаючою на деякому
проміжку, якщо більшому
значенню аргументу з цього
проміжку відповідає більше
значення функції.

3.

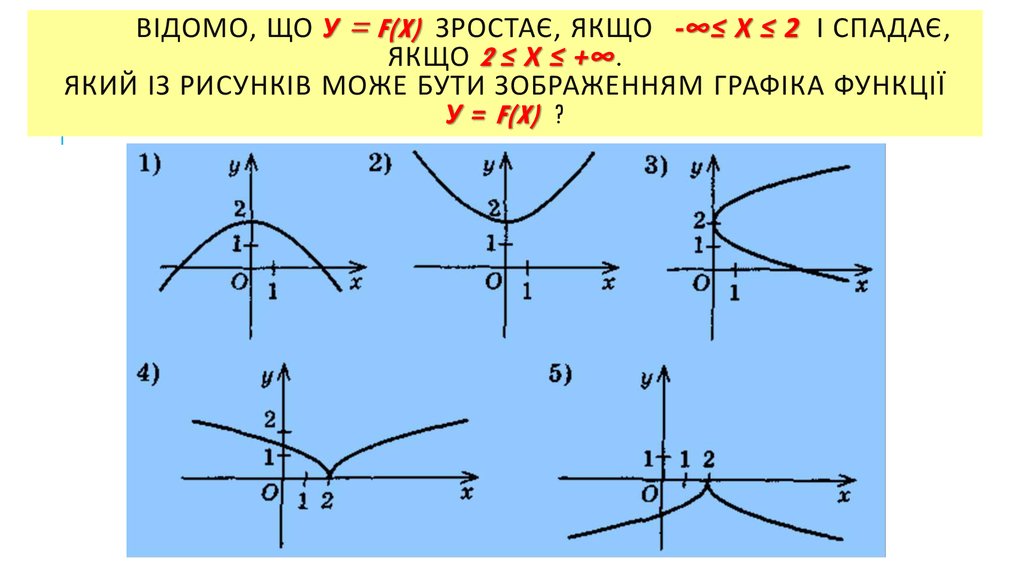
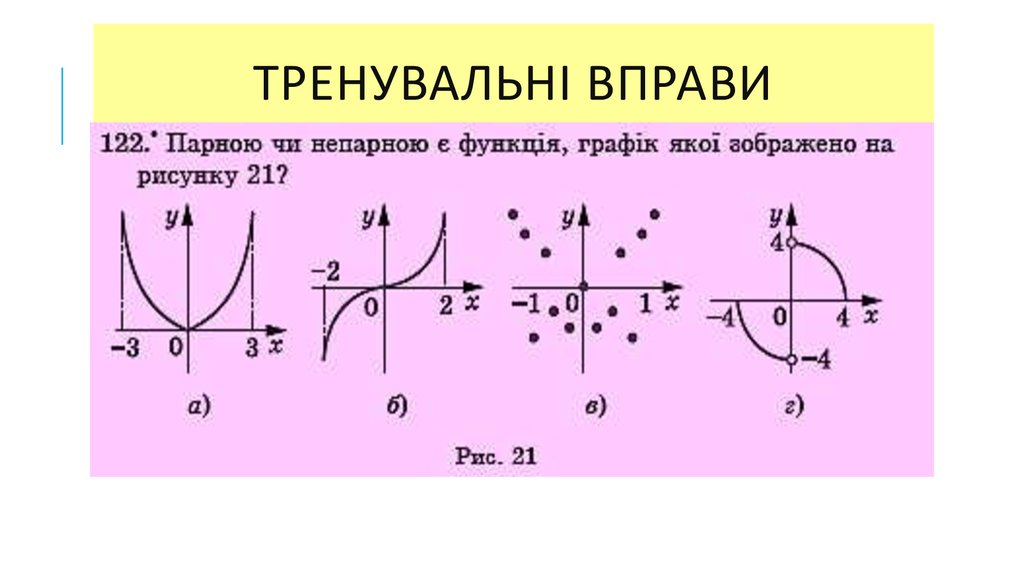
4. Відомо, що у = F(x) зростає, якщо -∞≤ х ≤ 2 і спадає, якщо 2 ≤ х ≤ +∞. Який із рисунків може бути зображенням графіка функції у = F(x) ?

ВІДОМО, ЩО У = F(X) ЗРОСТАЄ, ЯКЩО -∞≤ Х ≤ 2 І СПАДАЄ,
ЯКЩО 2 ≤ Х ≤ +∞.
ЯКИЙ ІЗ РИСУНКІВ МОЖЕ БУТИ ЗОБРАЖЕННЯМ ГРАФІКА ФУНКЦІЇ
У = F(X) ?

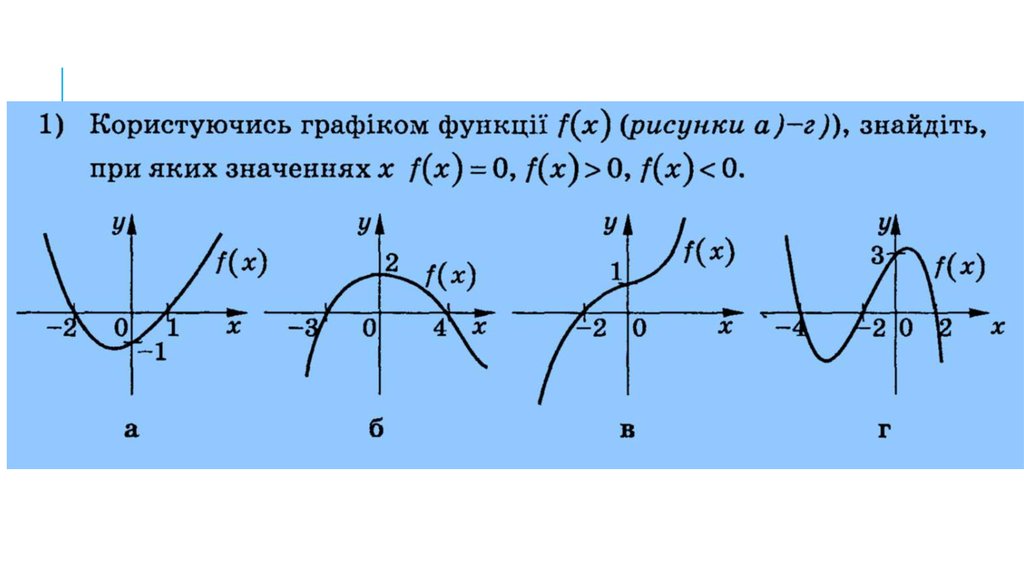
5.

6.

7.

Класна робота
Домашня робота

8. парні і непарні функції

ПАРНІ І НЕПАРНІ ФУНКЦІЇ

9. Парна функція

Означення. Функцію f
називають парною, якщо для
будь-якого x з області
визначення f
(–x) = f (x).
Очевидно, що функція y = x2
є парною.
Парна функція симетрична
відносно вісі ординат (ОУ).

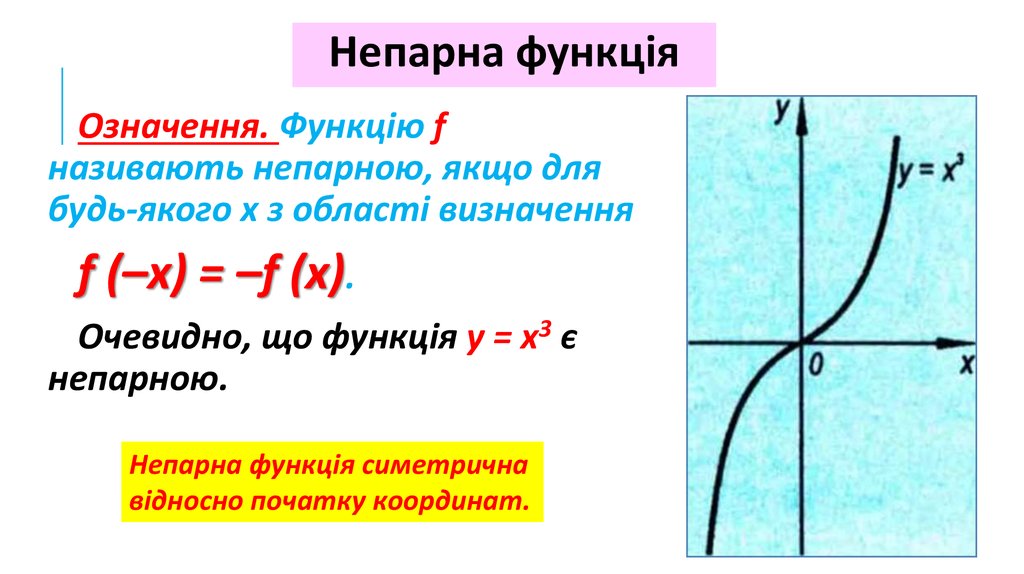
10. Непарна функція

Означення. Функцію f
називають непарною, якщо для
будь-якого x з області визначення
f (–x) = –f (x).
Очевидно, що функція y = x3 є
непарною.
Непарна функція симетрична
відносно початку координат.

11. Тренувальні вправи

ТРЕНУВАЛЬНІ ВПРАВИ

12. Тренувальні вправи

ТРЕНУВАЛЬНІ ВПРАВИ

13. Тренувальні вправи

ТРЕНУВАЛЬНІ ВПРАВИ

14. Тренувальні вправи

ТРЕНУВАЛЬНІ ВПРАВИ