Механические волны. Акустика

1.

Механические волны. Акустика
Распространение волн в упругой среде
Волновой процесс.
Основной физической моделью вещества является совокупность
движущихся и взаимодействующих между собой атомов и молекул.
Способы передачи энергии и импульса между двумя точками
пространства:
непосредственное перемещение частиц от точки к точке;
перенос энергии без переноса вещества в результате
последовательной передачи энергии и импульса по цепочке между
соседними взаимодействующими друг с другом частицами среды.
Волновой процесс — процесс переноса энергии без переноса
вещества.
Механическая волна — возмущение, распространяющееся в упругой
среде.
Наличие упругой среды — необходимое условие распространения
механических волн.
1

2.

Механические волны. Акустика
Распространение волн в упругой среде
Продольные волны.
Рис.1 – Волновой процесс
передачи энергии в
твёрдом теле
Рис.2 – Возникновение и
распространение
продольной волны в
твёрдом теле
2

3.

Механические волны. Акустика
Распространение волн в упругой среде
Скорость механической
возмущения в среде.
волны
—
скорость
распространения
Энергия взаимодействия крайних атомов правого конца стержня длиной
l передаётся маятнику 2 через промежуток времени t = l/v после удара
маятника 1 (рис.1).
Продольная волна — волна, в которой движение частиц среды
происходит вдоль направления распространения волны.
Продольные волны могут распространяться в любой среде.
3

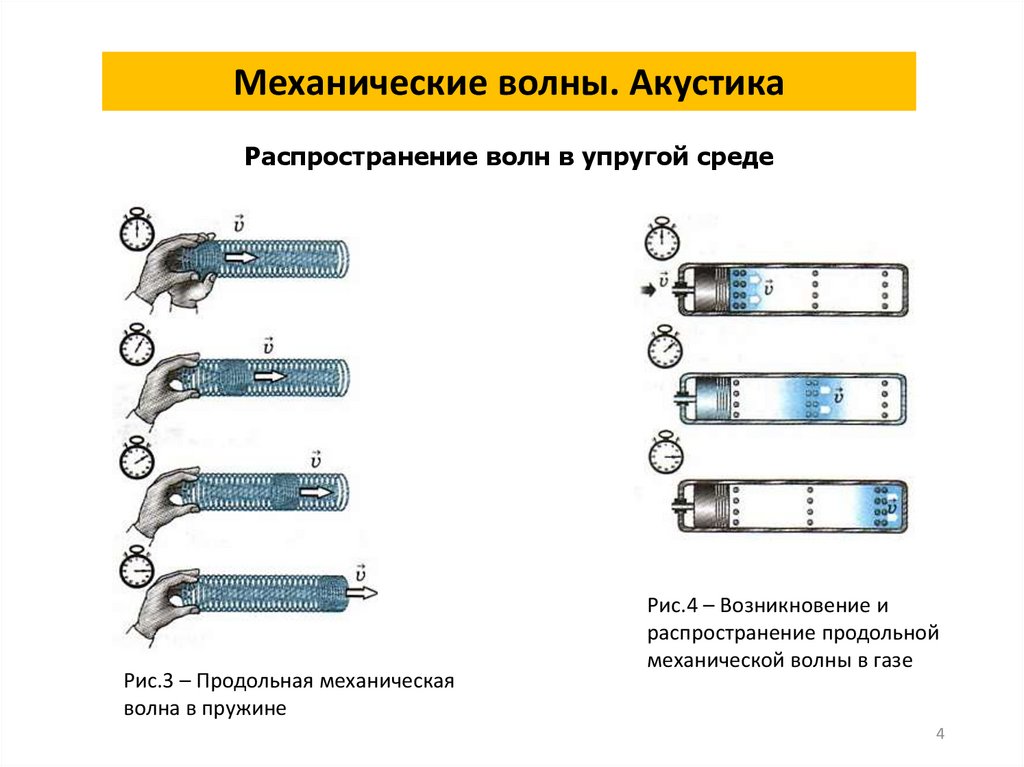
4.

Механические волны. Акустика
Распространение волн в упругой среде
Рис.3 – Продольная механическая
волна в пружине
Рис.4 – Возникновение и
распространение продольной
механической волны в газе
4

5.

Механические волны. Акустика
Распространение волн в упругой среде
Поперечные волны. В твёрдом теле из-за сильной связи частиц между
собой возможно возникновение поперечных волн.
Поперечная механическая волна — волна, в которой
частицы среды перемещаются перпендикулярно
направлению распространения волны.
Рис.6 – Возникновение и распространение
поперечных волн в твёрдом теле
Рис.5 – Поперечные
механические волны:
а)в пружине; б)в шнуре 5

6.

Механические волны. Акустика
Распространение волн в упругой среде
Поперечные волны в газах и жидкостях не возникают, так как газы и
жидкости не обладают упругостью формы.
Рис.7 – Распространение поперечных сейсмических волн:
а) поперечные волны в мантии;
б) огибание поперечными волнами жидкого ядра Земли
6

7.

Механические волны. Акустика
Распространение волн в упругой среде
Отражение волн.
Рис. 8 – Отражение поперечной
волны от закреплённого конца
шнура
Отражённая волна находится в противофазе
с падающей (рис.8).
Отражённая волна находится в фазе с
падающей (рис.9).
Рис. 9 – Отражение
поперечной волны от
свободного конца шнура
7

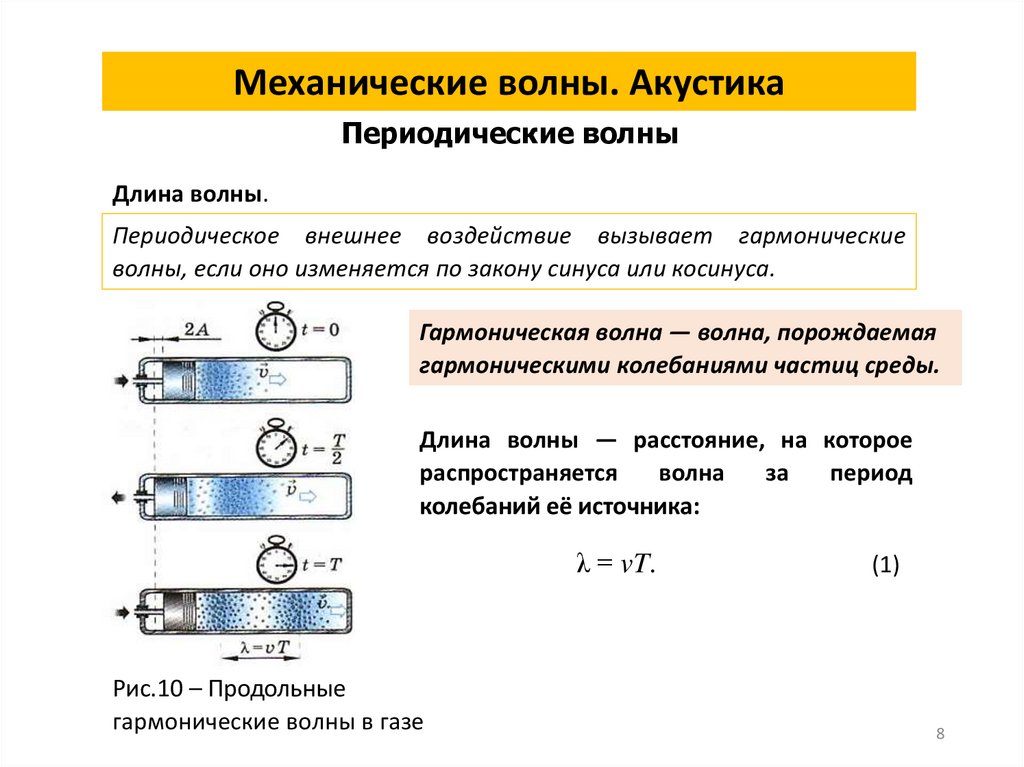
8.

Механические волны. Акустика
Периодические волны
Длина волны.
Периодическое внешнее воздействие вызывает гармонические
волны, если оно изменяется по закону синуса или косинуса.
Гармоническая волна — волна, порождаемая
гармоническими колебаниями частиц среды.
Длина волны — расстояние, на которое
распространяется
волна
за
период
колебаний её источника:
λ = vT.
Рис.10 – Продольные
гармонические волны в газе
(1)
8

9.

Механические волны. Акустика
Периодические волны
Рис.11 – Гармонические волны на поверхности жидкости:
а) при падении капель через равные промежутки времени;
б) при периодических колебаниях участка поверхности
Области сжатия соответствуют гребням волны, области разрежения —
впадинам.
9

10.

Механические волны. Акустика
Поляризация
Поляризация — пространственная
упорядоченность
направления
колебаний
частиц
среды
в
поперечной волне.
Плоскость поляризации —
плоскость,
в
которой
колеблются частицы среды
в волне.
Рис.12 – Прохождение через поляризатор
(щель) гармонической поперечной
механической волны, линейнополяризованной в плоскости XY
Линейно-поляризованная механическая волна — поперечная волна,
вызывающая колебания частицы среды вдоль определённого
направления (линии).
10

11.

Стоячие волны
Стоячая волна — волна,
образующаяся в результате
наложения двух гармонических
волн, распространяющихся
навстречу друг другу и имеющих
одинаковый период, амплитуду и
поляризацию.
Рис.13 – Образование
поперечных стоячих волн в
шнуре, закреплённом на конце
11

12.

Механические волны. Акустика
Стоячие волны
В поперечной стоячей волне каждая точка:
• совершает синхронно со всеми остальными его точками
гармонические колебания;
• колеблется перпендикулярно покоящемуся шнуру (оси X);
• колеблется с периодом, равным периоду внешнего возмущения;
• имеет собственную амплитуду колебаний.
Стоячая волна — волна, все точки которой колеблются с одинаковой
фазой.
Волну называют стоячей, так как энергия не переносится вдоль шнура,
а лишь трансформируется в поперечном направлении из
потенциальной в кинетическую, и наоборот.
Пучности стоячей волны — положения точек, имеющих максимальную амплитуду колебаний.
Узлы стоячей волны — неперемещающиеся
амплитуда колебаний которых равна нулю.
точки
волны,
12

13.

Механические волны. Акустика
Стоячие волны
Моды колебаний.
Если закреплены оба конца шнура (или струны), отражение волны
происходит от обоих концов. В этом случае расстояние между узлами
образующейся в шнуре (струне) стоячей волны не может быть
произвольным и зависит лишь от длины шнура (струны).
Дважды отражённая волна, распространяющаяся со скоростью V,
может усилить первоначальное воздействие, если достигнет правого
конца через промежуток времени 2l/v, кратный периоду внешнего
воздействия:
D струне будут поддерживаться только такие гармонические внешние
воздействия, длина волны (λ = vT) которых связана с длиной струны
соотношением
(2)
На длине струны, закреплённой на концах, укладывается целое
число п полуволн поперечных стоячих волн.
13

14.

Механические волны. Акустика
Стоячие волны
Рис.14 – Моды собственных
колебаний в струне,
закреплённой на концах.
На длине струны
укладывается целое число
полуволн собственных
колебаний
(3)
Мода колебаний, соответствующая п = 1, называется первой
гармоникой собственных колебаний или основной модой.
14

15.

Механические волны. Акустика
Стоячие волны
Для произвольного п > 1 соответствующая
мода колебаний называется п-й гармоникой
или п-м обертоном.
В пучностях воздух колеблется сильнее
всего, в узлах он неподвижен.
Рис.15 – Продольные собственные колебания газа в цилиндре:
а) первая гармоника; б) вторая гармоника;
Δх — смещение молекул от положения равновесия в
определённый момент времени
15

16.

Механические волны. Акустика
Звуковые волны
Звуковые волны — упругие волны в среде, вызываюцие у человека
слуховые ощущения.
Изучению звука посвящена специальная область физики — акустика.
Инфразвуковые волны (v < 16 Гц), имеющие малую частоту,
вызываются источниками, размеры которых превышают расстояния,
характерные для повседневного опыта человека.
Миллиметровые источники могут генерировать ультразвуковые волны
(v > 20 кГц).
Необходимое условие распространения звуковых волн — наличие
упругой среды.
Скорость распространения звуковых волн определяется скоростью
передачи взаимодействия между частицами.
Чем больше потенциальная энергия взаимодействия молекул
вещества, тем больше скорость звука
vт т > vж > vг
16

17.

Механические волны. Акустика
Звуковые волны
Высота звука.
Высота звука определяется частотой источника звуковых
колебаний. Чем больше частота колебаний, тем выше звук.
Эффект Доплера.
предсказан в 1842 г. австрийским физиком
Кристианом Доплером.
Эффект Доплера — зависимость
частоты
сигнала,
фиксируемого
приёмником, от скорости движения
источника и приёмника.
17

18.

Механические волны. Акустика
Звуковые волны
Зависимость высоты звука от скорости движения источника
Рис.16 – Зависимость высоты звука от
скорости движения источника:
а) неподвижный источник сигнала:
частоты сигнала, воспринимаемые
наблюдателями 1 и 2, совпадают с
частотой v0 сигнала источника;
б) движущийся вправо источник сигнала:
частота звука, воспринимаемая
наблюдателем 1, выше частоты v0 сигнала
источника; частота v2 звука,
воспринимаемого наблюдателем 2, ниже
частоты v0
18

19.

Механические волны. Акустика
Звуковые волны
Волна II дойдёт до наблюдателя 1 через время
(4)
после волны I, а до наблюдателя 2 — через время
(5)
частота сигнала, воспринимаемого наблюдателями 1 и 2,
(6)
Это означает, что vи1 > v0, a vи2 < v0.
(7)
(8)
знак «минус» соответствует случаю приближения источника к
приемнику, а знак «плюс» — случаю удаления источника от
приемника.
19

20.

Механические волны. Акустика
Звуковые волны
Рис.17 – Звуковые волны
сжатия при различной
скорости движения
источника:
а) vи = 0;
б) vи < vзв.;
в) vи = vзв;
г) vи > vзв
sin α = vзв/ vи
20

21.

Рис.18 – преодоление истребителем звукового барьера
21

22.

Механические волны. Акустика
Звуковые волны
Зависимость высоты звука от скорости движения приемника.
(9)
(10)
частота сигнала
(11)
Рис.19 – Зависимость высоты звука от
скорости движения источника:
частота v1 звука, воспринимаемая
наблюдателем 1, выше частоты v0 сигнала
источника; частота v2 звука,
воспринимаемого наблюдателем 2, ниже
частоты v0
(12)
Это означает, что
v1 > v0, a v2 < v0.
(13)
знак «плюс» соответствует
случаю сближения приемника с
источником
22

23.

Механические волны. Акустика
Звуковые волны
Зависимость высоты звука от относительной скорости
движения источника и приёмника.
Зная частоту v0 и измеряя частоту v1, 2, можно найти относительную
скорость vотн движения приемника и источника, если vпр « v и vи « v.
(14)
(15)
где vотн = vпр+ vи Знак «плюс» соответствует случаю сближения
приемника и источника, а знак «минус» — их удалению друг от друга.
Если vпр, vи << с частота электромагнитных волн, фиксируемая
приёмником, движущимся со скоростью vотн относительно источника,
задаётся подобно (15)
(16)
23

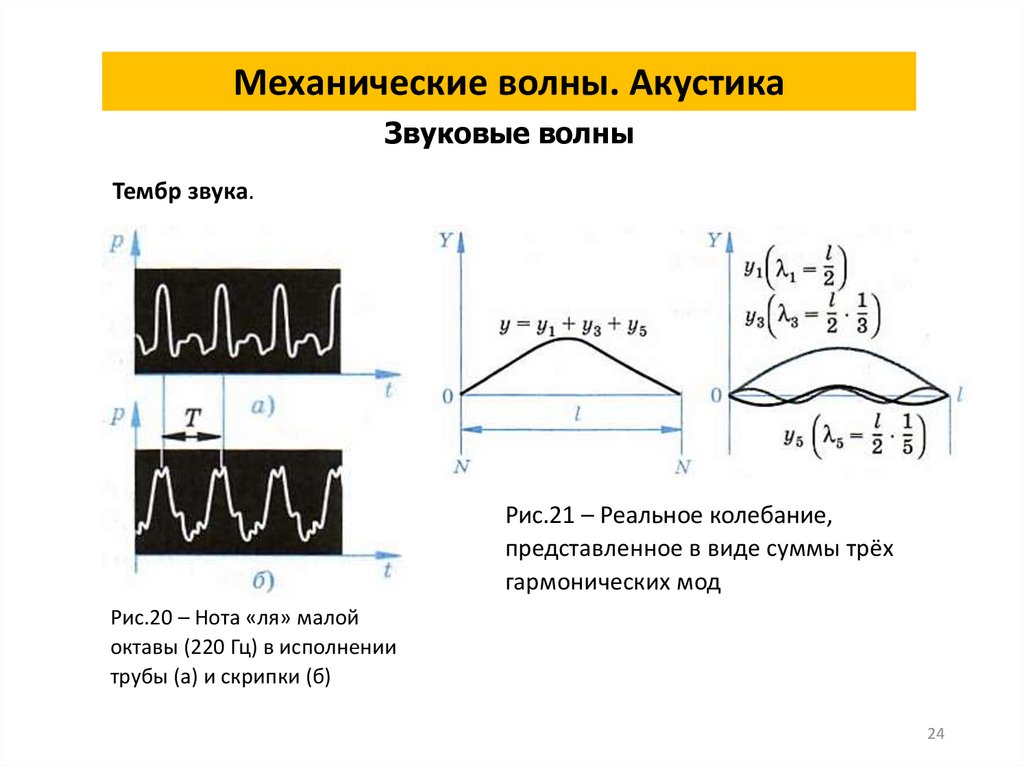
24.

Механические волны. Акустика
Звуковые волны
Тембр звука.
Рис.21 – Реальное колебание,
представленное в виде суммы трёх
гармонических мод
Рис.20 – Нота «ля» малой
октавы (220 Гц) в исполнении
трубы (а) и скрипки (б)
24

25.

Механические волны. Акустика
Звуковые волны
Рис.22 – Относительная амплитуда основной моды (220
Гц) и обертонов при исполнении ноты «ля» малой
октавы: а) на фортепиано; б) контральто
25

26.

Механические волны. Акустика
Звуковые волны
26

27.

Механические волны. Акустика
Звуковые волны
Тембр звука определяется формой звуковых колебаний. Различие
формы колебаний, имеющих одинаковый период, связано с разной
относительной амплитудой основной моды и обертонов.
Изменение давления в звуковой волне влияет на громкость звука.
Громкость звука зависит от амплитуды колебаний давления в
звуковой волне.
Интенсивность звука — отношение падающей на поверхность
звуковой мощности к площади этой поверхности.
Единица интенсивности звука — ватт на квадратный метр (Вт/м2).
Порог слышимости соответствует интенсивности звука I0 = 10–12 Вт/м2;
болевой порог I б п = 1 Вт/м2.
27

28.

Механические волны. Акустика
Звуковые волны
Уровень интенсивности звука — десятичный логарифм отношения двух
интенсивностей звука (единица — белл (Б)):
где I — интенсивность звука, I0 — порог слышимости.
(17)
За единицу уровня интенсивности звука принят 1 дБ (децибелл).
Увеличение интенсивности звука на 10 дБ примерно удваивает
громкость.
Уровень интенсивности 120 дБ является болевым порогом.
28

29.

Механические волны. Акустика
Звуковые волны
29