Ошибки классификации. Экспериментальная оценка качества алгоритмов классификации (лекция 03)

1.

Передовая инженерная аэрокосмическая школа
Искусственный интеллект и машинное
обучение
Лекция 03
Ошибки классификации.
Экспериментальная
оценка качества алгоритмов
классификации.
https://do.ssau.ru/moodle/course/view.php?id=1459

2.

Пример расчёта вероятности
Пусть некий тест на какую-нибудь болезнь имеет вероятность успеха
95%
◦ 5% — вероятность как позитивной, так и негативной ошибки.
Всего болезнь имеется у 1% респондентов.
Пусть некий человек получил позитивный результат теста
◦ тест говорит, что он болен.
С какой вероятностью он действительно болен?
Пусть: t-результат теста; d-наличие болезни.
P d 1 P(d 1 t 1) P(t 1) P(d 1 t 0) P(t 0)
По теореме Байеса
P d 1 t 1
P t 1 d 1 P t 1
P d 1 t 1 P t 1 P d 1 t 0 P t 0
0,95 0,01
0,95 0,01 0,05 0,99
Ответ: 16%
2/28

3.

Виды ошибок
Допустим, существует «основной класс».
◦ Обычно, это класс, при обнаружении которого, предпринимается
какое-либо действие;
◦ Например, при постановке диагноза основным классом будет
«болен», а вторичным классом «здоров».
Измерения ошибки, как оценки «вероятности выдать неверный
ответ», может быть не всегда достаточно:
◦ 16% ошибки при постановке диагноза может означать как и то
что, 16 % больных будут признаны здоровыми
(и возможно умрут от отсутствия лечения), так и то, что 16%
здоровых больными (и деньги на лечение будут потрачены зря).
При неравнозначности ошибок для разных классов вводят понятие
ошибки первого и второго рода и замеряют их по отдельности.
3/28

4.

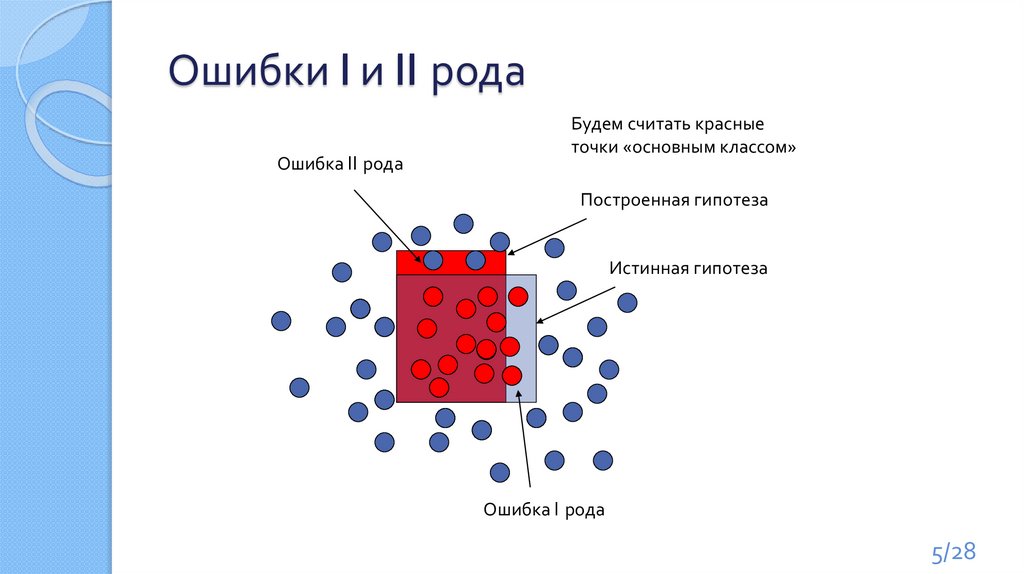
Ошибки I и II рода
Ошибка первого рода равна вероятности принять основной класс за
вторичный
◦ Вероятность «промаха», когда искомый объект будет пропущен
Ошибка второго рода равна вероятности принять вторичный класс
за основной
◦ Вероятность «ложной тревоги», когда за искомый объект будет принят «фон»
Особенно важно оценивать ошибки I и II рода раздельно при
несбалансированности классов:
◦ Пусть P( y 1) 0,01; P( y 1) 0,99
◦ Тогда при нулевой ошибке II рода
и ошибке I рода P(a( x) 1 | y 1) 0,5
◦ Общая ошибка всего лишь P(a( x) y ) 0,005
4/28

5.

Ошибки I и II рода
Ошибка II рода
Будем считать красные
точки «основным классом»
Построенная гипотеза
Истинная гипотеза
Ошибка I рода
5/28

6.

Регулировка баланса
Почти все алгоритмы
классификации допускают
регулировку ошибок I и II рода
за счёт варьирования
некоторого параметра
6/28

7.

Анализ ошибок классификации
yi 1; 1
Алгоритм классификации a ( xi ) 1; 1
Задача классификации на 2 класса
Ответ классификатора
Правильный ответ
TP, True Positive
a(xi )=+1
yi =+1
TN, True Negative
a(xi )= −1
yi = −1
FP, False Positive - ошибка I рода
a(xi )= +1
yi = −1
FN, False Negative - ошибка II рода
a(xi )= −1
yi =+1
1 l
TP TN
Accuracy a( xi ) yi
l i 1
TP TN FP FN
– доля правильных ответов алгоритма
Недостаток: не учитывается ни численность (дисбаланс)
классов, ни цена ошибки на объектах разных классов.
7/28

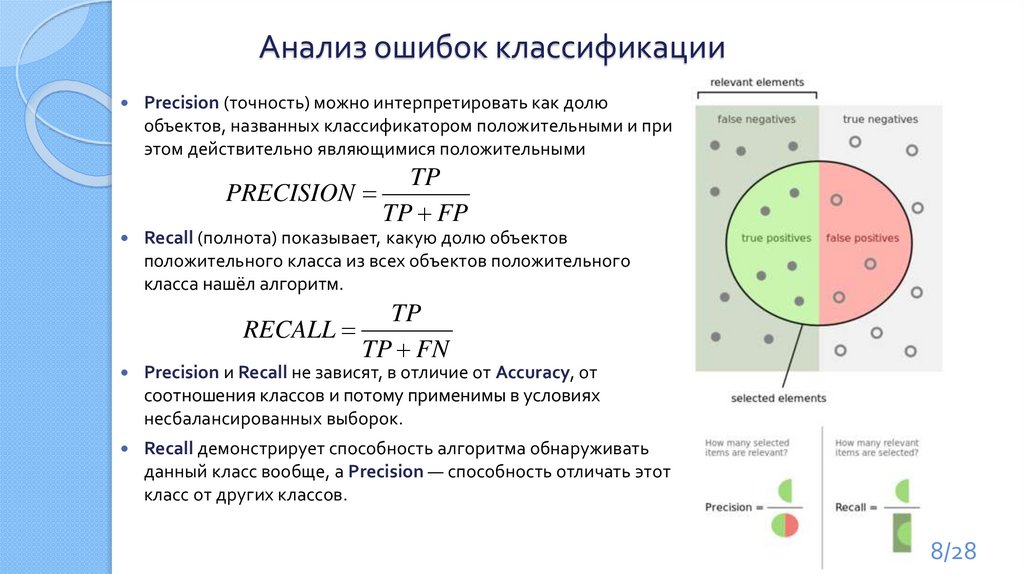
8.

Анализ ошибок классификации
Precision (точность) можно интерпретировать как долю
объектов, названных классификатором положительными и при
этом действительно являющимися положительными
TP
PRECISION
TP FP
Recall (полнота) показывает, какую долю объектов
положительного класса из всех объектов положительного
класса нашёл алгоритм.
TP
RECALL
TP FN
Precision и Recall не зависят, в отличие от Accuracy, от
соотношения классов и потому применимы в условиях
несбалансированных выборок.
Recall демонстрирует способность алгоритма обнаруживать
данный класс вообще, а Precision — способность отличать этот
класс от других классов.
8/28

9.

Анализ ошибок классификации
Существует несколько различных способов объединить precision и recall
в агрегированный критерий качества.
F-мера — среднее гармоническое precision и recall
F 1 2
* recall
precision
precision recall
2
β в данном случае определяет вес точности в метрике
F-мера достигает максимума при полноте и точности, равными единице,
и близка к нулю, если один из аргументов близок к нулю.
◦ в случае задач с несбалансированными классами, которые превалируют в реальной
практике, часто приходится прибегать к техникам искусственной модификации
выборок для выравнивания соотношения классов.
9/28

10.

Чувствительность vs Избирательность
Чувствительность – вероятность дать правильный ответ на пример
основного класса: sensitivity SE P(a( x) y | y 1)
Избирательность – вероятность дать правильный ответ на пример
вторичного класса: specificity SP P(a( x) y | y 1)
TPR ( True Positive Rate) : показатель положительного результата оценки
среди всех фактически положительных образцов – Скорость отзыва
положительных образцов или покрытия.
FPR ( False Positive Rate) : соотношение ошибочно оценённых
положительных значений среди всех фактически отрицательных выборок
– Скорость отзыва отрицательных образцов или уровень фальсификации
◦ Общее количество истинно положительных категорий в выборке составляет TP + FN.
◦ Общее количество истинных контрпримеров в выборке равно FP + TN.
TP
TPR
TP FN
FP
FPR
FP TN
Домашнее задание 4:
Написать выражение зависимостей
между SE, SP, TPR и FPR.
10/28

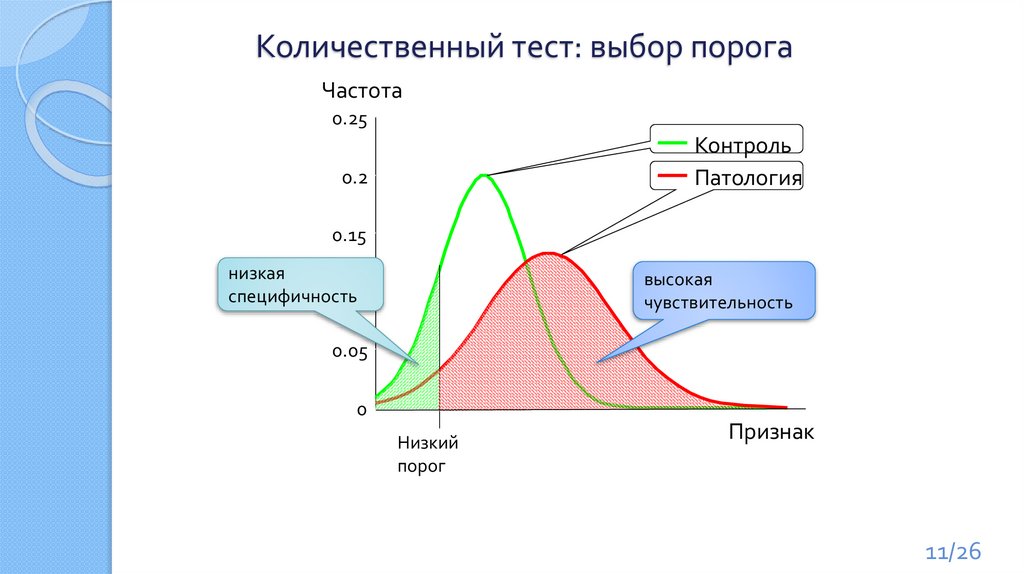
11.

Количественный тест: выбор порога
Частота
0.25
Контроль
Патология
0.2
0.15
низкая
0.1
специфичность
высокая
чувствительность
0.05
0
Низкий
порог
Признак
11/26

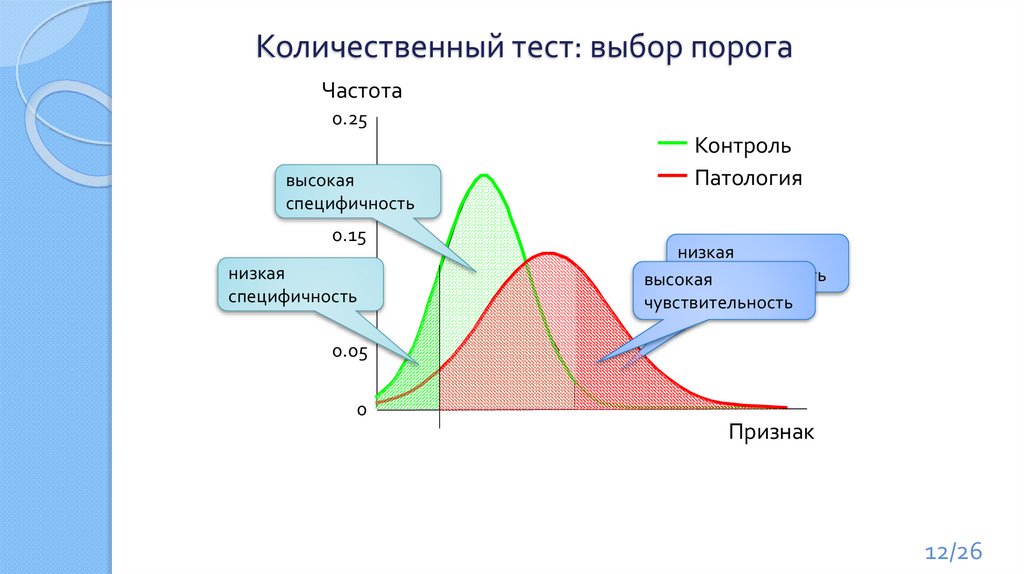
12.

Количественный тест: выбор порога
Частота
0.25
0.2
высокая
специфичность
0.15
низкая
0.1
специфичность
Контроль
Патология
низкая
чувствительность
высокая
чувствительность
0.05
0
Признак
12/26

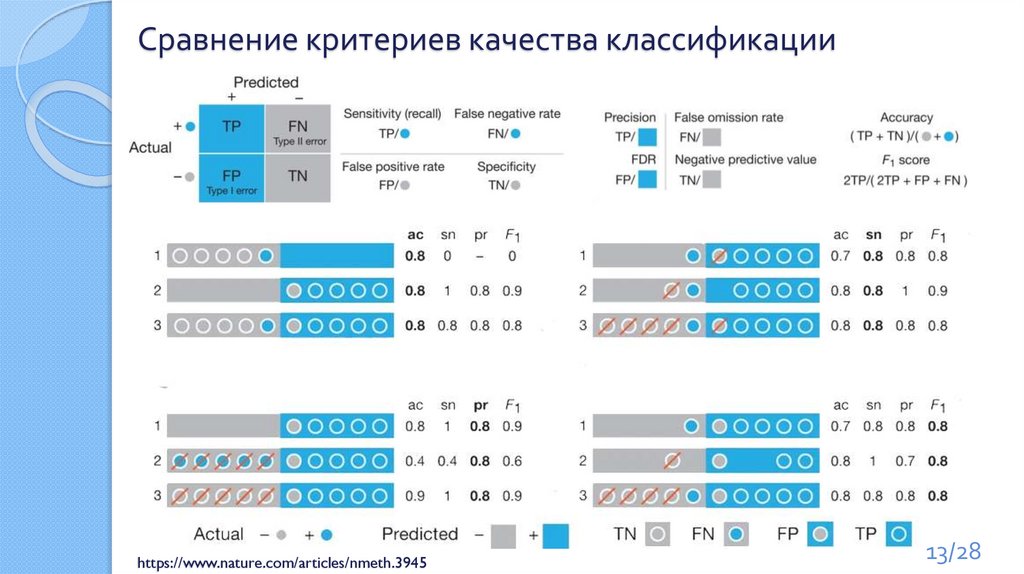
13.

Сравнение критериев качества классификации
https://www.nature.com/articles/nmeth.3945
13/28

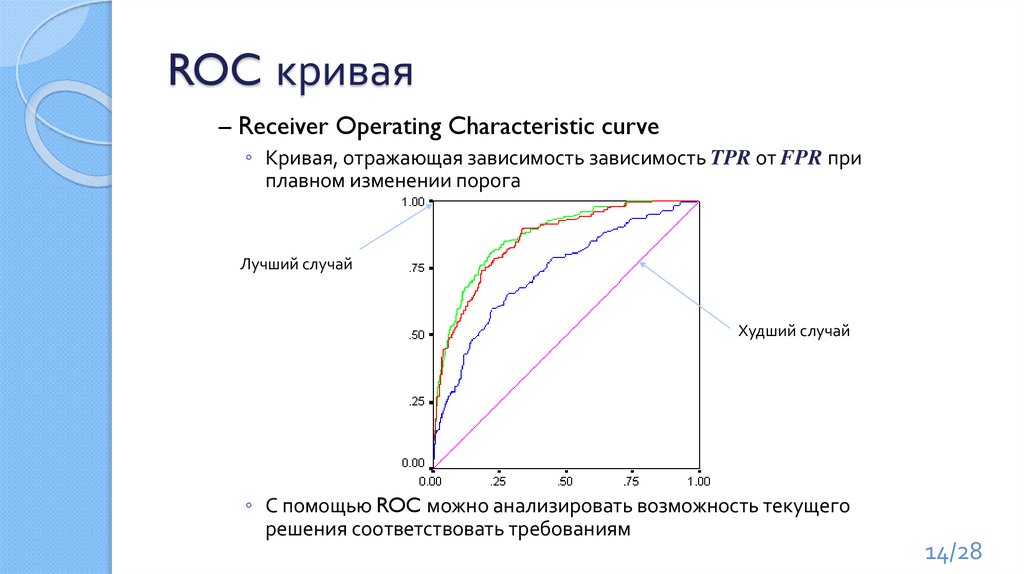
14.

ROC кривая
– Receiver Operating Characteristic curve
◦ Кривая, отражающая зависимость зависимость TPR от FPR при
плавном изменении порога
Лучший случай
Худший случай
◦ С помощью ROC можно анализировать возможность текущего
решения соответствовать требованиям
14/28

15.

Построение ROC кривой
TPR
Частота
0.25
Контроль
Патология
0.2
1
0.15
0.5
0.1
0.05
FPR
0
Пороговое
значение
Признак
0
0.5
1
Оптимальный выбор порога:
выбирается точка на ROC-кривой, которая ближе всех
к левому верхнему углу (0,1)
15/28

16.

Форма ROC кривых
Признак не работает
1
SE
0
1 - SP
1
0
1 - SP
1 1 тест
1
1
Идеальный признак
SE
2 тест
1-ый тест лучше, чем 2-ой
SE
0
1 - SP
1
16/28

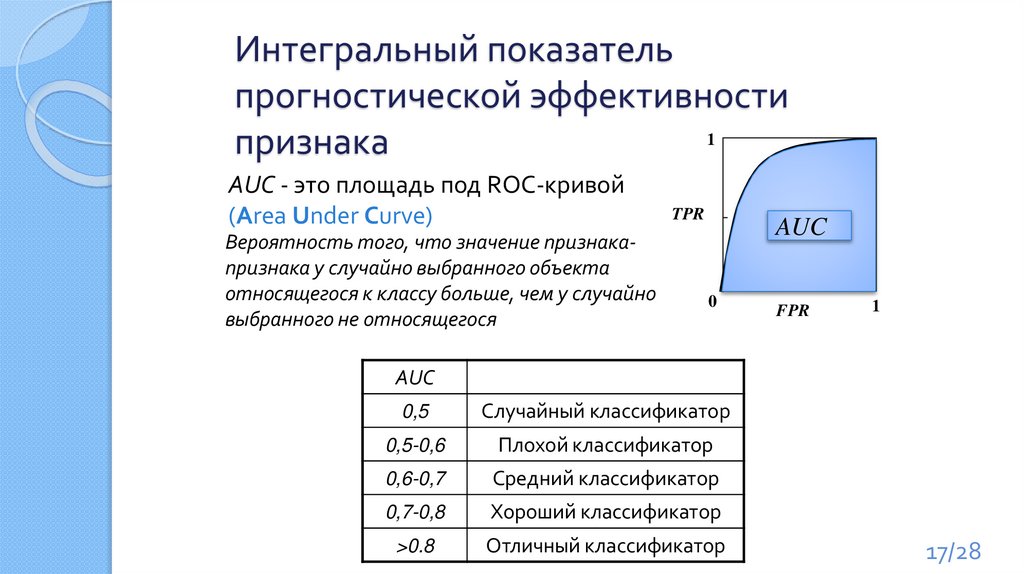
17.

Интегральный показатель
прогностической эффективности
1
признака
AUC - это площадь под ROC-кривой
(Area Under Curve)
Вероятность того, что значение признакапризнака у случайно выбранного объекта
относящегося к классу больше, чем у случайно
выбранного не относящегося
TPR
AUC
0
FPR
1
AUC
0,5
Случайный классификатор
0,5-0,6
Плохой классификатор
0,6-0,7
Средний классификатор
0,7-0,8
Хороший классификатор
>0.8
Отличный классификатор
17/28

18.

Методы экспериментальной оценки качества
алгоритмов
Теоретические оценки общего риска
◦ Нетривиально рассчитываются для конкретных алгоритмов
◦ Сильно завышены
◦ Как следствие, для практической задачи малоинформативны
Для конкретной задачи, желательно получить точные
количественные оценки качества работы
Используются экспериментальные методы
◦ удерживание
◦ скользящий контроль
◦ и др.
18/28

19.

Удерживание
Вспомним, что такое общий риск:
R(a, X ) PX l a( x) y P( x) a( x) y dx
X
◦ Его минимизация для нас является основной целью
◦ Однако, напрямую его посчитать невозможно (требует вычислений на
неограниченном множестве)
Оценим общий риск ошибкой на некотором конечном подмножестве X
не пересекающимся с обучающей выборкой:
c
1
R ( a, X ) ~ P a ( x ) y | X c a ( x j ) y j
c j 1
19/28

20.

Удерживание
Пусть, имеется набор данных с известными ответами
X k x1 ,..., xk
Разобьём
Xl Xc Xk :Xl Xc 0
Будем использовать для обучения
, а для контроля
l
X
Оценим общий риск ошибкой на подмножестве X с не
c
X
пересекающимся с обучающей выборкой:
c
1
R ( a, X ) ~ P a ( x ) y | X c a ( x j ) y j
c j 1
20/28

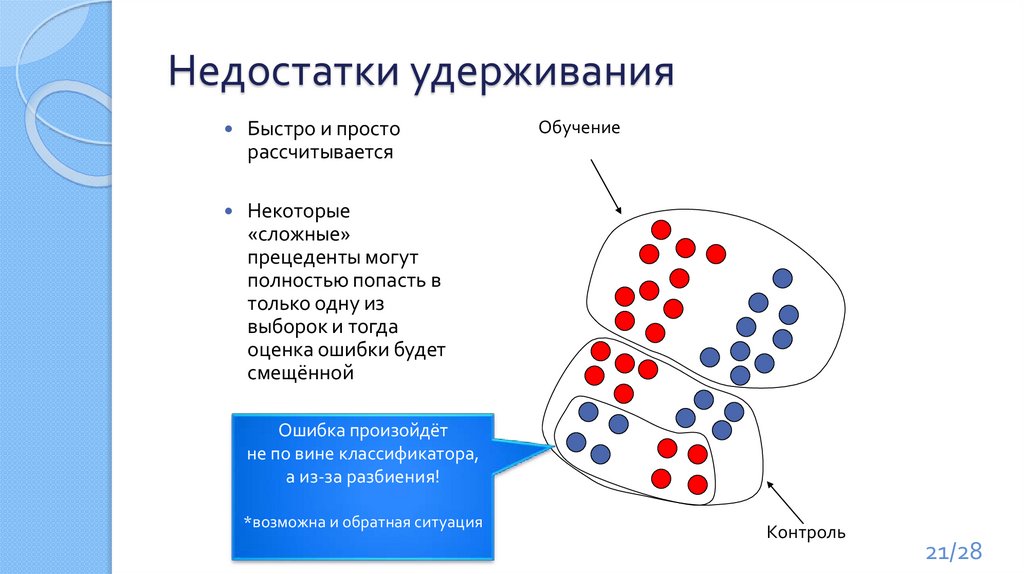
21.

Недостатки удерживания
Быстро и просто
рассчитывается
Некоторые
«сложные»
прецеденты могут
полностью попасть в
только одну из
выборок и тогда
оценка ошибки будет
смещённой
Обучение
Ошибка произойдёт
не по вине классификатора,
а из-за разбиения!
*возможна и обратная ситуация
Контроль
21/28

22.

Повторное удерживание
Если разбиение на контроль и обучение может быть не устойчивым, то
почему бы не провести его много раз и не усреднить?
◦ Такой методикой мы частично избавимся от проблемы «сложных прецедентов»;
◦ НО, вероятность того, что какие-то прецеденты ни разу не попадут в контрольную
выборку всё равно велика;
◦ Процесс становится сильно рандомизированным;
22/28

23.

Скользящий контроль
Разделим выборку на множество непересекающихся частей и будем
поочерёдно использовать одно из них для контроля, а остальные для
тренировки
X : X X 0, i j
◦ Разбиваем:
i f
1
i
j
f
i
k
X
X
i 1
◦ Приближаем риск:
1 f
P( ( X ) y ) P( ( X i ) y * | X i )
f i 1
j i
k
*
23/28

24.

Скользящий контроль
Разделим выборку на множество непересекающихся частей и будем
поочерёдно использовать одно из них для контроля, а остальные для
тренировки
X k x1 ,..., xk
X1
X2
Контроль
X3
X4
X5
Результат считается как средняя
ошибка по всем итерациям
Обучение
24/26

25.

Свойства скользящего контроля
В пределе равен общему риску
Каждый прецедент будет один раз присутствовать в контрольной
выборке
Обучающие выборки будут сильно перекрываться (чем больше
сегментов, тем больше перекрытие)
◦ Если один группа «сложных прецедентов» попала полностью в один сегмент, то
оценка будет смещенной
25/28

26.

Скользящий контроль лучше повторного удерживания?
Вероятность пропустить хотя бы один прецедент при
повторном удерживании:
P (1 ) n k
◦ - доля прецедентов в контрольной выборке
◦ k - количество прецедентов всего
◦ n - количество итераций
n
log P
k
log(1 )
При 0.5; k 1000; n 10
P 0.510 1000 0.9766
Вероятность, что прецеденты будут выбраны в равных долях
ещё меньше!!!
26/28

27.

Эвристические алгоритмы повышения
точности оценок
Бустинг (boosting)
Базовые алгоритмы строятся последовательно, для каждого базового
алгоритма, начиная со второго, веса обучающих объектов пересчитываются
так, чтобы он точнее настраивался на тех объектах, на которых чаще
ошибались все предыдущие алгоритмы. Веса алгоритмов также
вычисляются исходя из числа допущенных ими ошибок.
Бустинг представляет собой жадный алгоритм построения композиции
алгоритмов.
Наиболее известен алгоритм AdBoost предложенный в 1995 г. Шапиром
(Schapire R. The boosting approach to machine learning: An overview // MSRI
Workshop on Nonlinear Estimation and Classification, Berkeley, CA. - 2001.)
27/28

28.

Эвристические алгоритмы повышения
точности оценок
Баггинг (bagging — «bootstrap aggregation»),
в отличие от бустинга все элементарные классификаторы обучаются и
работают параллельно (независимо друг от друга). Идея заключается в том,
что классификаторы не исправляют ошибки друг друга, а компенсируют их при
голосовании.
Предложен Л. Брейманом (Breiman L. Arcing classifiers // The Annals of Statistics. –
1998. – Vol. 26, no. 3. – Pp. 801−849.), производится взвешенное голосование
базовых алгоритмов, обученных на различных подвыборках данных, либо на
различных частях признакового описания объектов.
Базовые классификаторы должны быть независимыми, это могут быть
классификаторы основанные на разных группах методов или же обученные на
независимых наборах данных. Во втором случае можно использовать один и
тот же метод.
Из множества объектов обучающей выборки формируются бутстреп- выборки
– случайные подмножества объектов, как правило с повторами.
28/28