Similar presentations:
Расчёт установившихся режимов в линейной электрической цепи при периодических воздействиях
1.
РАСЧЁТ УСТАНОВИВШИХСЯ РЕЖИМОВ ВЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ ЦЕПИ ПРИ
ПЕРИОДИЧЕСКИХ ВОЗДЕЙСТВИЯХ
Консультация 2
Методы рассчета ЭЦ
2.
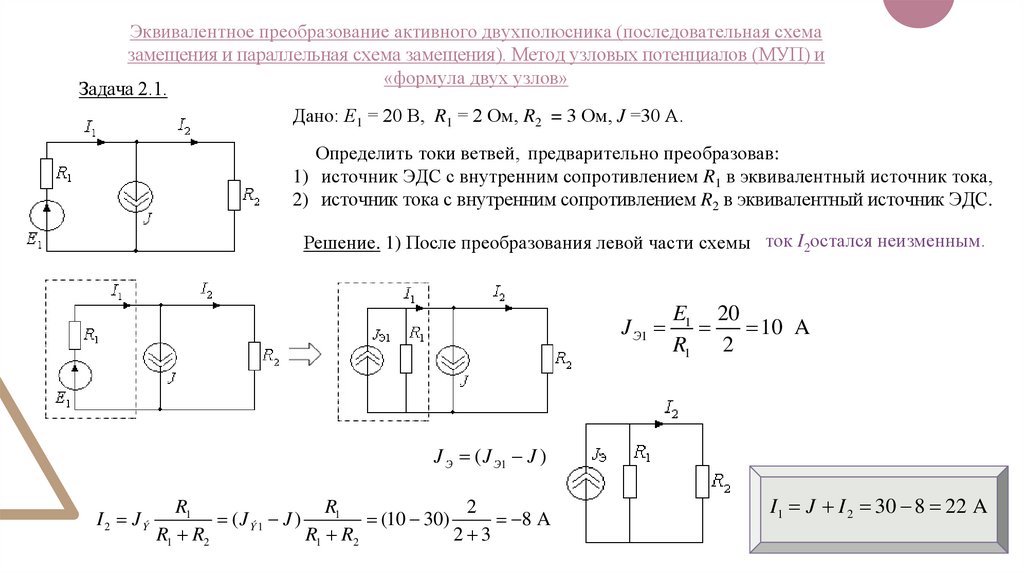
Эквивалентное преобразование активного двухполюсника (последовательная схемазамещения и параллельная схема замещения). Метод узловых потенциалов (МУП) и
«формула двух узлов»
Задача 2.1.
Дано: Е1 = 20 В, R1 = 2 Ом, R2 = 3 Ом, J =30 А.
Определить токи ветвей, предварительно преобразовав:
1) источник ЭДС с внутренним сопротивлением R1 в эквивалентный источник тока,
2) источник тока с внутренним сопротивлением R2 в эквивалентный источник ЭДС.
Решение. 1) После преобразования левой части схемы ток I2остался неизменным.
J Э1
E1 20
10 A
R1 2
J Э ( J Э1 J )
I2 JÝ
R1
R1
2
( J Ý1 J )
(10 30)
8 A
R1 R2
R1 R2
2 3
I1 J I 2 30 8 22 A
3.
2) После преобразования правой части схемы ток I1 остался неизменным.EЭ 2 J R2 30 3 90 B
E1 EÝ 2
I1
22 A
R1 R2
I 2 I1 J 22 30 8 A
4.
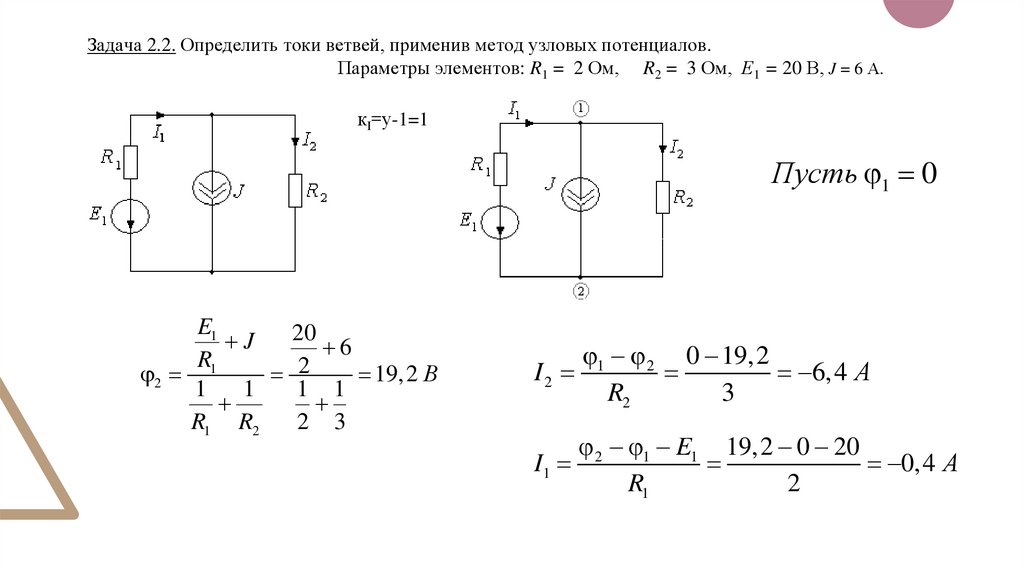
Задача 2.2. Определить токи ветвей, применив метод узловых потенциалов.Параметры элементов: R1 = 2 Ом, R2 = 3 Ом, Е1 = 20 В, J = 6 А.
кI=у-1=1
Пусть 1 0
E1
20
J
6
R1
2
2
19,2 В
1
1
1 1
R1 R2
2 3
1 2 0 19,2
I2
6,4 А
R2
3
2 1 E1 19,2 0 20
I1
0,4 А
R1
2
5.
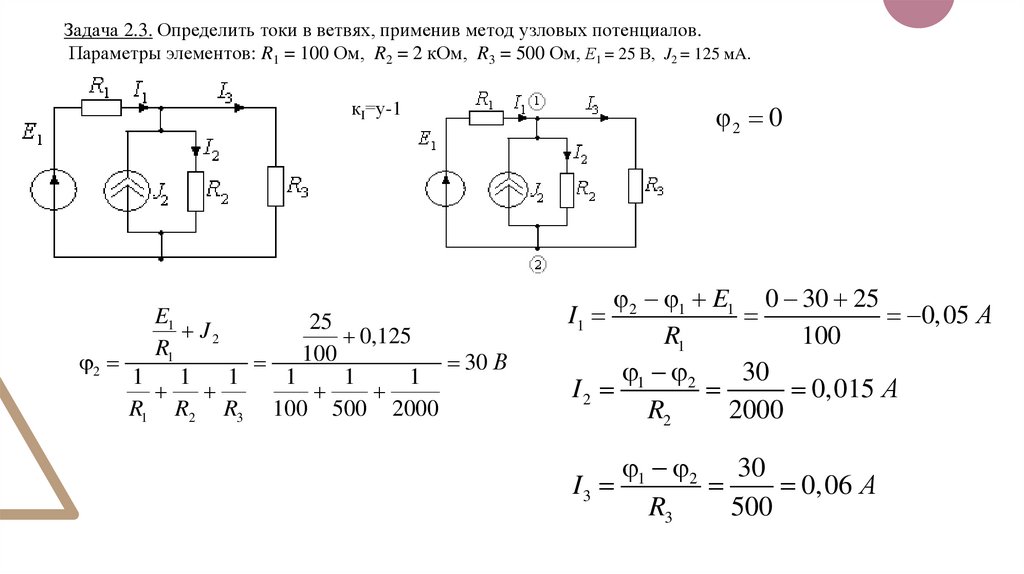
Задача 2.3. Определить токи в ветвях, применив метод узловых потенциалов.Параметры элементов: R1 = 100 Ом, R2 = 2 кОм, R3 = 500 Ом, Е1 = 25 В, J2 = 125 мA.
кI=у-1=1
E1
25
J2
0,125
R1
100
2
30 В
1
1
1
1
1
1
R1 R2 R3 100 500 2000
2 0
2 1 E1 0 30 25
I1
0,05 А
R1
100
1 2
30
I2
0,015 А
R2
2000
1 2 30
I3
0,06 А
R3
500
6.
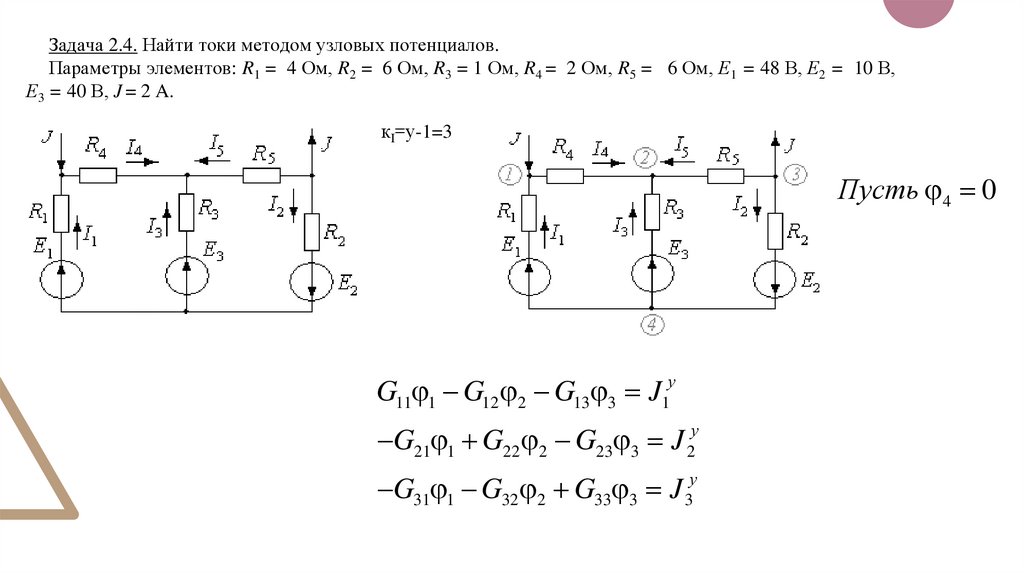
Задача 2.4. Найти токи методом узловых потенциалов.Параметры элементов: R1 = 4 Ом, R2 = 6 Ом, R3 = 1 Ом, R4 = 2 Ом, R5 = 6 Ом, Е1 = 48 В, Е2 = 10 В,
Е3 = 40 В, J = 2 A.
кI=у-1=3
Пусть 4 0
G11 1 G12 2 G13 3 J1у
G21 1 G22 2 G23 3 J 2у
G31 1 G32 2 G33 3 J 3у
7.
G11 1 G12 2 G13 3 J1уG21 1 G22 2 G23 3 J 2у
G31 1 G32 2 G33 3 J 3у
Собственные проводимости узловых потенциалов:
Взаимные проводимости
1
1
G33
R5 R2
1
G13 G31 0 G23 G32
R5
1
G12 G21
R4
Узловые источники токов ветвей
1
1
1
G22
R13 R4 R5
1
1
G11
R1 R4
E1
J J
R1
у
1
1 44 B
E3
J
R3
у
2
2 38 B
E2
J J
R2
у
3
3 8 B
8.
4 1 E1I1
1 A
R1
3 4 E2
I2
3 A
R2
4 2 E3
I3
2A
R3
1 2
I4
3 A
R4
3 2
I5
5 A
R5
9.
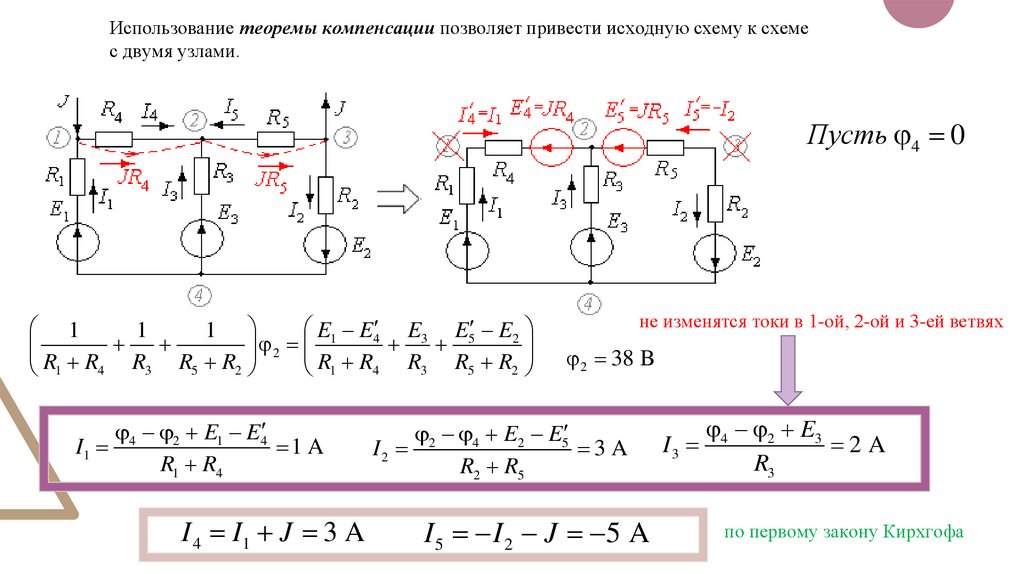
Использование теоремы компенсации позволяет привести исходную схему к схемес двумя узлами.
Пусть 4 0
1
E1 E4 E3 E5 E2
1
1
2
R
R
R
R
R
R
R
R
R
R
4
3
5
2
4
3
5
2
1
1
4 2 E1 E4
I1
1 A
R1 R4
I 4 I1 J 3 A
не изменятся токи в 1-ой, 2-ой и 3-ей ветвях
2 38 B
4 E2 E5
I2 2
3 A
R2 R5
I 5 I 2 J 5 A
4 2 E3
I3
2A
R3
по первому закону Кирхгофа
10.
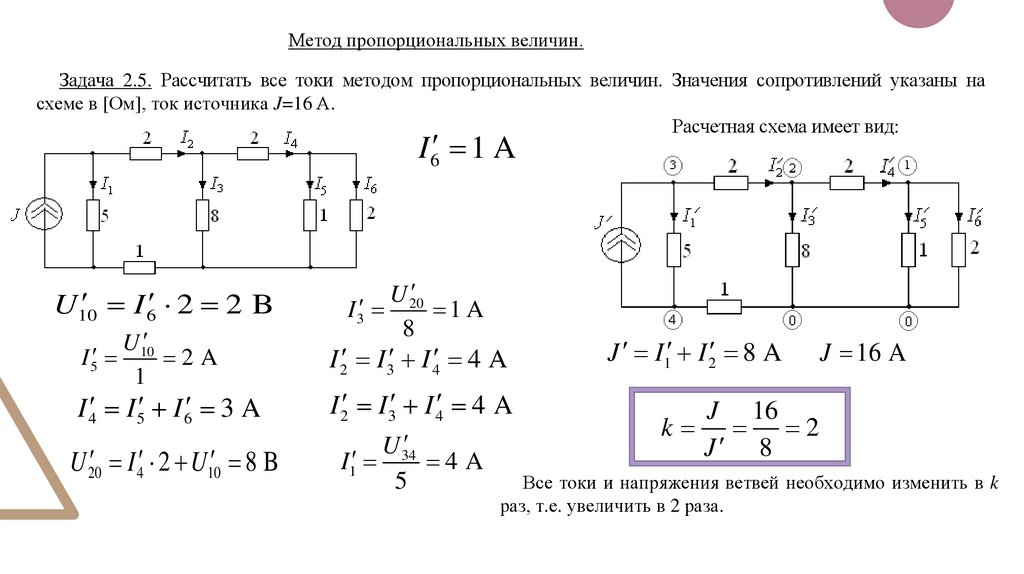
Метод пропорциональных величин.Задача 2.5. Рассчитать все токи методом пропорциональных величин. Значения сопротивлений указаны на
схеме в [Ом], ток источника J=16 А.
Расчетная схема имеет вид:
I 6 1 A
I 6 2 2 B
U10
U10
I 5
2A
1
I 4 I 5 I 6 3 A
U 20 I 4 2 U10 8 B
U 20
I 3
1 A
8
I 2 I 3 I 4 4 A
I 2 I 3 I 4 4 A
U 34
I1
4A
5
J I1 I 2 8 A
J 16 A
J 16
k 2
J 8
Все токи и напряжения ветвей необходимо изменить в k
раз, т.е. увеличить в 2 раза.
11.
Метод наложенияЗадача 2.6. Определить токи I1 и I2 методом наложения. При каком значении тока источника J ток I1 станет в два
раза больше и поменяет свое направление? Параметры элементов цепи: R1 = 2 Ом, Е1 = 20 В, R2 = 3 Ом, J 3= 6 А.
Частичная схема от источника Е1
(J=0):
I1 I1( E1 ) I1( J3 )
I 2 I 2( E1 ) I 2( J3 )
Частичная схема от источника J
(Е1=0):
12.
I1 I( E1 )
1
I
( J3 )
1
4 3,6 0,4 A
входную проводимость
I 2 I 2( E1 ) I 2( J3 ) 4 2,4 6,4 A
I1( E1 ) 4
g11
0,2 См
E1
20
коэффициент передачи по току
Согласно принципу наложения
I1( J3 ) 3,6
k13
0,6
J3
6
I1 I1( E1 ) I1( J3 ) g11E1 k13 J 3 0,2 E1 0,6 J 3
Для того чтобы ток первой ветви стал в два раза больше и
поменял свое направление, т.е.
при Е1 = 20 В ток источника тока должен быть
J 3
I1 I1 ( 0,4) 0,8 A
0,8 0,2 20
8 A
0,6
13.
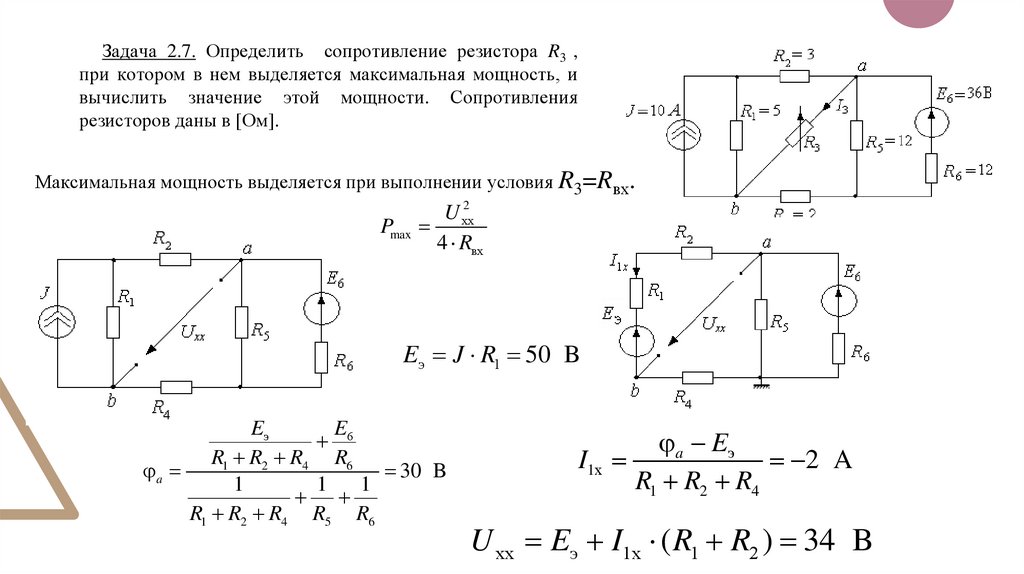
Задача 2.7. Определить сопротивление резистора R3 ,при котором в нем выделяется максимальная мощность, и
вычислить значение этой мощности. Сопротивления
резисторов даны в [Ом].
Максимальная мощность выделяется при выполнении условия R3=Rвх.
2
U хх
Pmax
4 Rвх
Eэ J R1 50 B
Eэ
E6
R1 R2 R4 R6
a
30 B
1
1
1
R1 R2 R4 R5 R6
a Eэ
I1х
2 A
R1 R2 R4
U хх Eэ I1х ( R1 R2 ) 34 B
14.
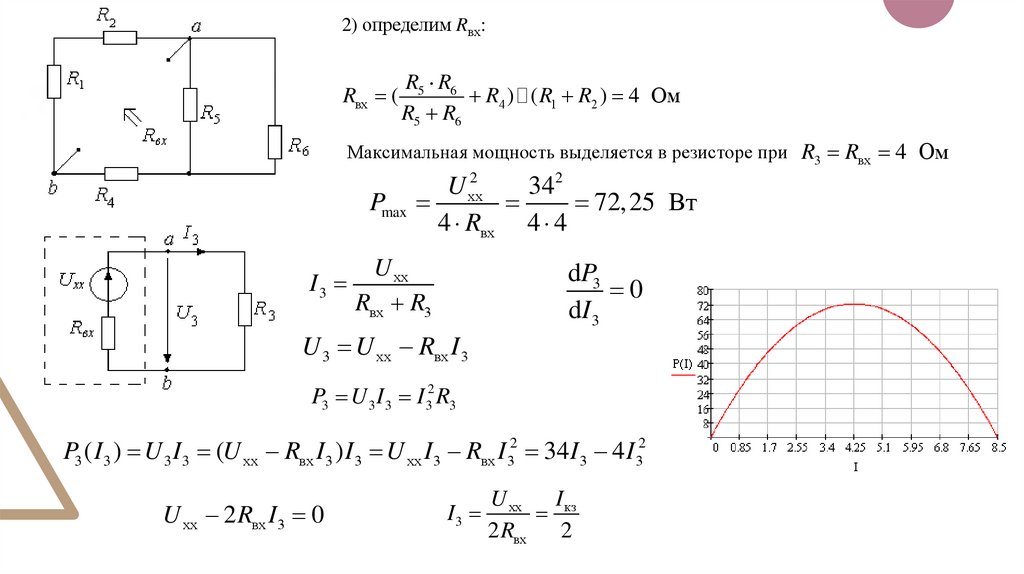
2) определим Rвх:Rвх (
R5 R6
R4 ) ( R1 R2 ) 4 Ом
R5 R6
Максимальная мощность выделяется в резисторе при R3 Rвх 4 Ом
2
U хх
342
Pmax
72,25 Вт
4 Rвх 4 4
U хх
I3
Rвх R3
U 3 U хх Rвх I 3
dP3
0
dI 3
P3 U 3 I 3 I 32 R3
P3 ( I 3 ) U 3 I 3 (U хх Rвх I 3 ) I 3 U хх I 3 Rвх I 32 34 I 3 4 I 32
U хх 2 Rвх I 3 0
I3
U хх I кз
2 Rвх
2
15.
КУРСОВАЯ РАБОТАРАСЧЁТ УСТАНОВИВШИХСЯ РЕЖИМОВ В ЛИНЕЙНОЙ ЭЛЕКТРИЧЕСКОЙ
ЦЕПИ ПРИ ПЕРИОДИЧЕСКИХ ВОЗДЕЙСТВИЯХ
e(t ) E0 Em sin(k t )
J (t ) J 0 J m sin(k t )
E0
n
В
2
Em
N 2
В,
2
n
J 0 10 3 А, J N 2 10 3 А
m
3
2
где N -номер группы студента, n-номер студента по журналу,
к-номер гармоники,
3
.
10 рад сек
R1 250 Ом, R2 500 Ом
R3 250 Ом, R4 300 Ом
R5 200 Ом, Rн 200 Ом
L 0,25Гн, C 4,8 10 6 Ф
E0 15 В, Em 6 2 В,
J 0 10 мА, J m 6 2 мА
Рассчитаем схемы при действии постоянных источников
16.
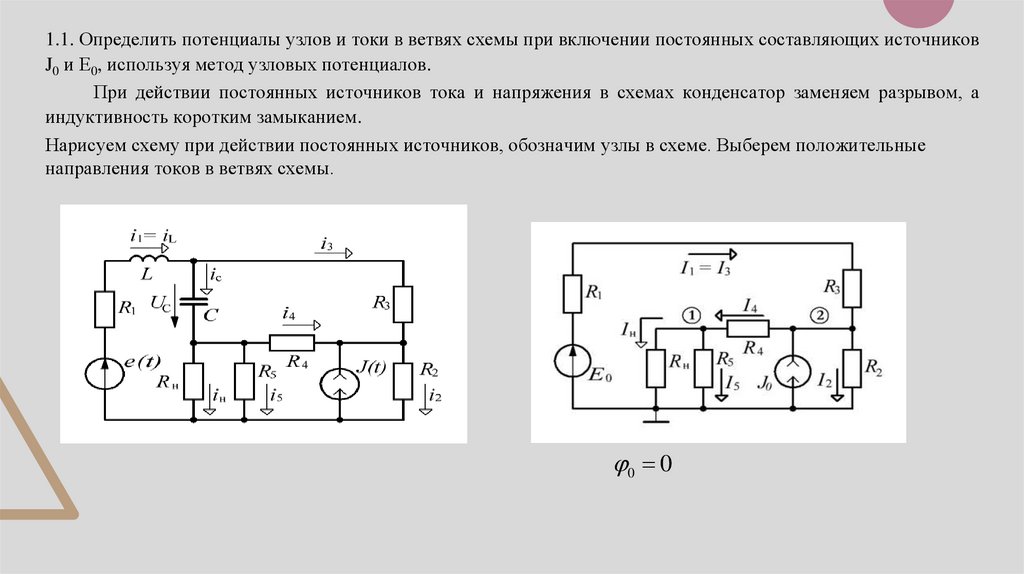
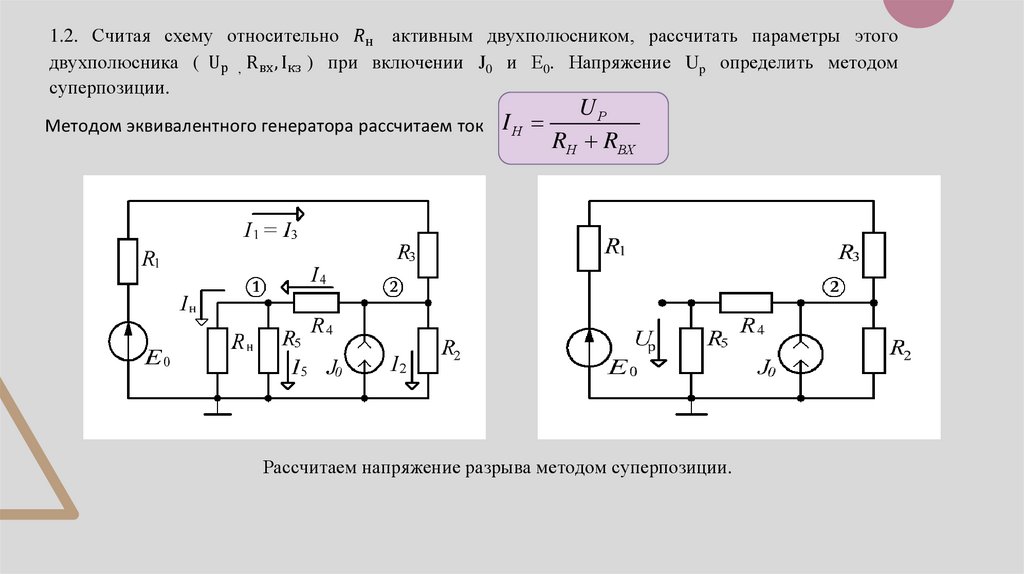
1.1. Определить потенциалы узлов и токи в ветвях схемы при включении постоянных составляющих источниковJ0 и Е0, используя метод узловых потенциалов.
При действии постоянных источников тока и напряжения в схемах конденсатор заменяем разрывом, а
индуктивность коротким замыканием.
Нарисуем схему при действии постоянных источников, обозначим узлы в схеме. Выберем положительные
направления токов в ветвях схемы.
0 0
17.
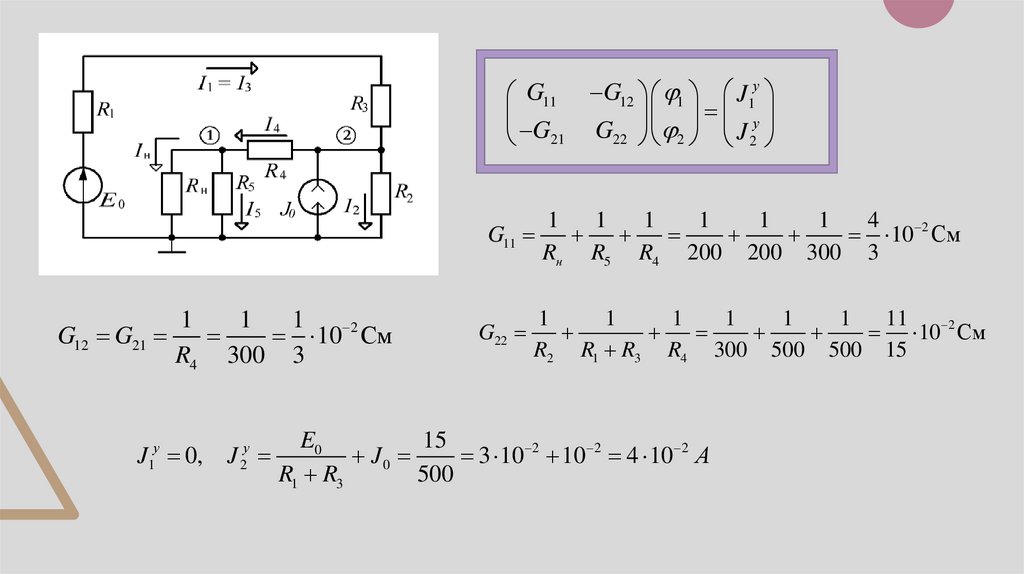
G11 G12 1 J1уу
G
21 G22 2 J 2
G11
1
1
1
G12 G21
10 2 См
R4 300 3
J1у 0,
J 2у
G22
1
1
1
1
1
1
4
10 2 См
Rн R5 R4 200 200 300 3
1
1
1
1
1
1
11
10 2 См
R2 R1 R3 R4 300 500 500 15
E0
15
J0
3 10 2 10 2 4 10 2 А
R1 R3
500
18.
4 23 10
1 10 2
3
1
10 2
1 0
3
11 2 2 4 10 2
10
15
G11 1 G12 2 0
G21 1 G22 2 4 10 2
G11
4 10 2 3
2 1
4 1
2
G12
3 10 1
15 4 20
1
1,54 В,
39
13
80
2 6,15 В
13
5 10 2 44 10 2
1
4 10 2
15
19.
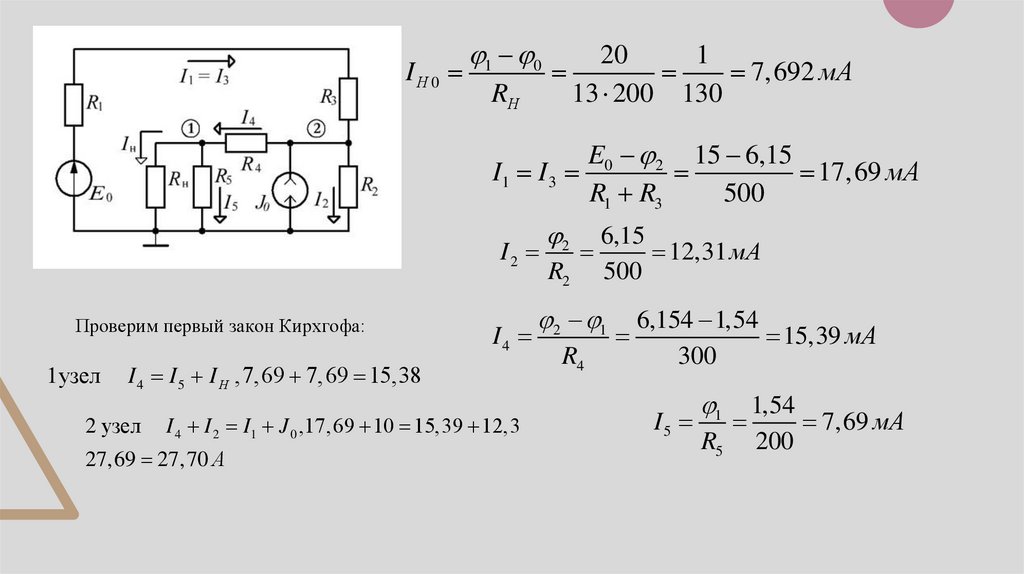
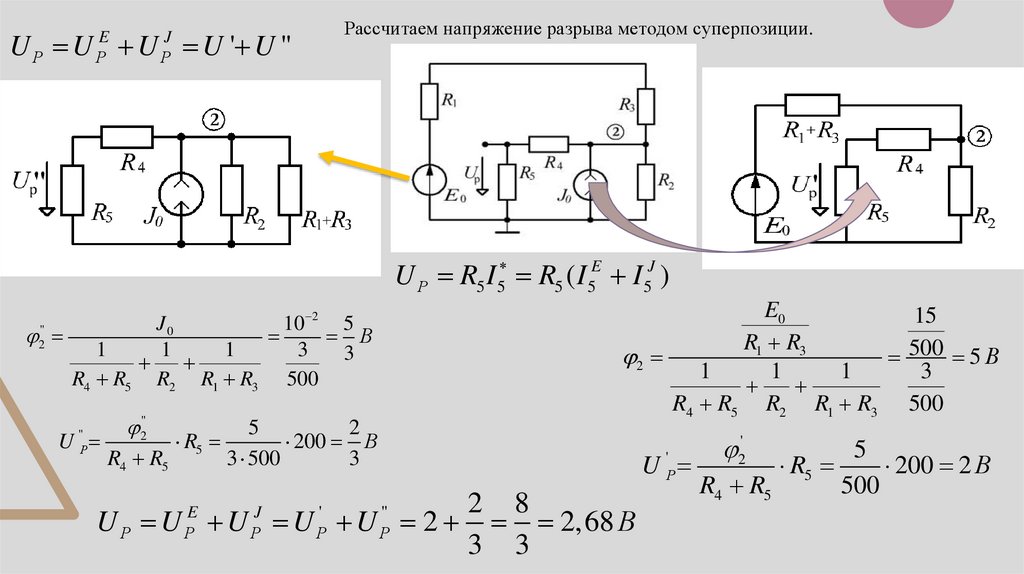
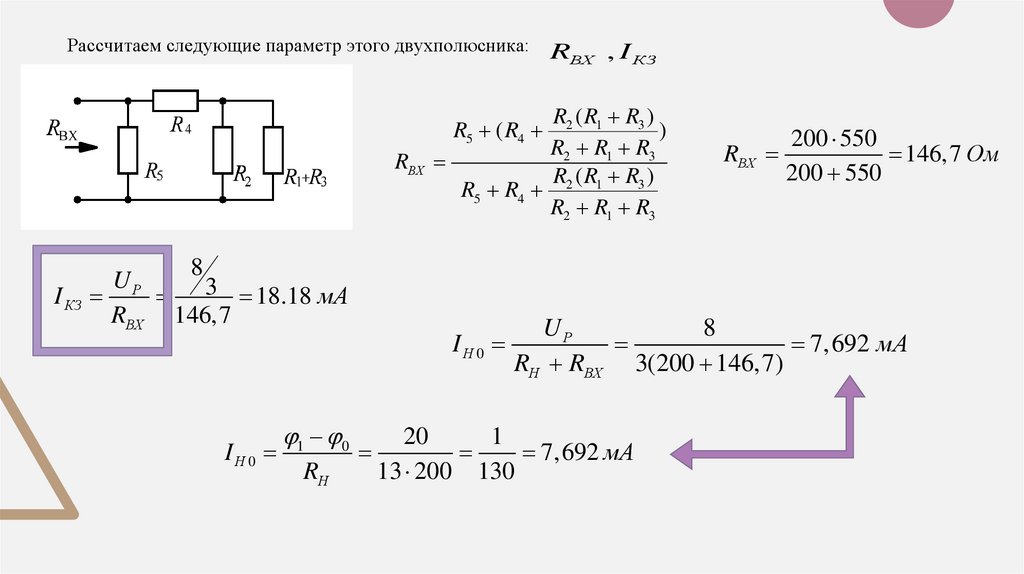
IН 01 0
RН
20
1
7,692 мА
13 200 130
E0 2 15 6,15
I1 I 3
17,69 мА
R1 R3
500
2
6,15
I2
12,31 мА
R2 500
Проверим первый закон Кирхгофа:
1узел
I4
I 4 I 5 I Н ,7,69 7,69 15,38
2 узел
I 4 I 2 I1 J 0 ,17,69 10 15,39 12,3
27,69 27,70 А
2 1
R4
6,154 1,54
15,39 мА
300
I5
1
R5
1,54
7,69 мА
200







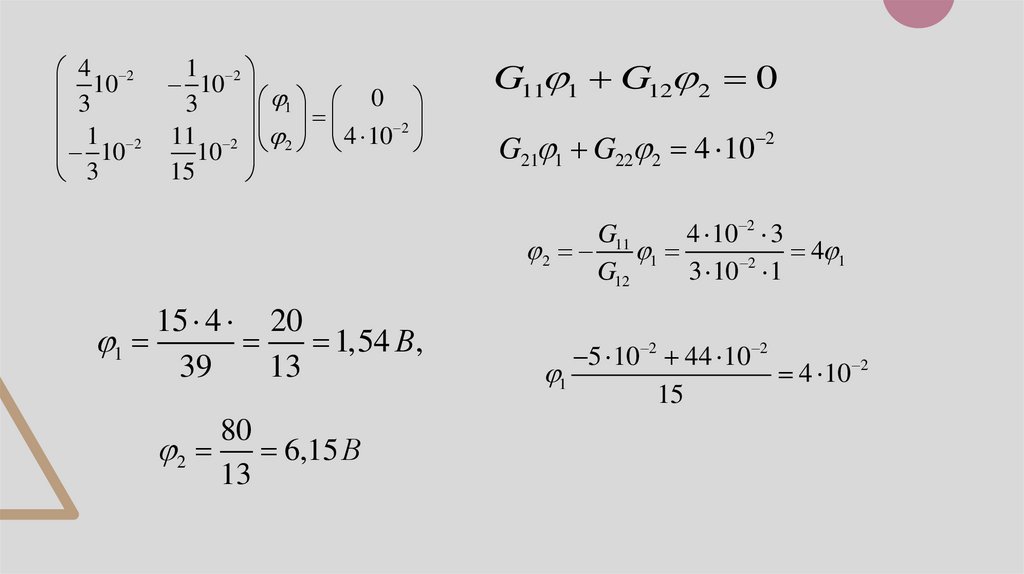

 physics
physics








