Similar presentations:
Тема 5. Транспортная задача
1. Тема 5. Транспортная задача.
2.
Транспортная задача2
3.
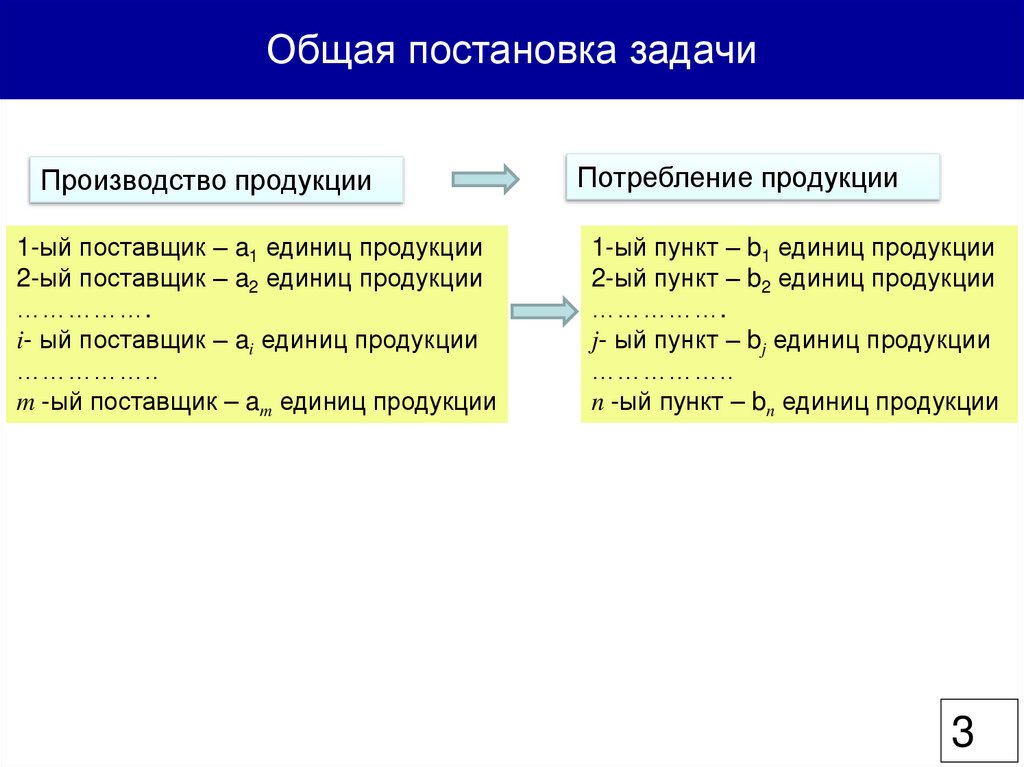
Общая постановка задачиПроизводство продукции
1-ый поставщик – a1 единиц продукции
2-ый поставщик – a2 единиц продукции
…………….
i- ый поставщик – ai единиц продукции
……………..
m -ый поставщик – am единиц продукции
Потребление продукции
1-ый пункт – b1 единиц продукции
2-ый пункт – b2 единиц продукции
…………….
j- ый пункт – bj единиц продукции
……………..
n -ый пункт – bn единиц продукции
3
4.
Общая постановка задачиМатрица транспортных расходов
с11 с1п
С
ст1 стп
сi,j – стоимость перевозки из i-го пункта
производства в j-й пункт назначения
План перевозок
х11 х1п
Х
хт1 хтп
xi,j – количество единиц перевозимого
продукта из i-го пункта производства в
j-й пункт назначения
4
5.
ОграниченияПлан называется допустимым, если хij, i = 1,…,т, j = 1,…,п
удовлетворяют следующим естественным условиям:
хij 0, i 1,...,т,
j 1,...,п,
хi1 хi 2 хiп аi , i 1,...,т,
х1 j х2 j хтj b j ,
j 1,...,п,
из i-го пункта производства
перевозится по всем j=1,2,…, n
пунктам назначения
в j-й пункт назначения
поступила продукция из
всех i=1,2 ,…, m пунктов
производства
То есть, все что произведено – перевезено потребителям,
а то что требовалось поставщикам – доставлено.
5
6.
Сведение к задаче линейного программированияТранспортная задача состоит в отыскании среди допустимых планов
перевозок оптимального, то есть такого, по которому общая
стоимость перевозок минимальна. Для этого необходимо найти
минимум целевой функции:
m n
z ci , j x i , j
i 1 j 1
при ограничениях
хij 0, i 1,..., т, j 1,..., п,
хi1 хi 2 хiп аi , i 1,..., т,
х1 j х2 j хтj b j , j 1,..., п,
Необходимое условие совместности
т
п
i 1
j 1
аi b j .
6
7.
Сведение к задаче линейного программированияТранспортная задача является задачей линейного
программирования и может быть решена симплекс-методом, но в
силу специфики ограничений для ее решения созданы и менее
громоздкие алгоритмы (метод потенциалов, венгерский метод).
В данной работе необходимо сначала решить задачу численно в
Excel, а затем провести ручной счет по методу потенциалов,
используя в качестве первоначального плана распределение по
методу наименьшей стоимости или северо-западного угла.
7
8.
Заданиеa1 a,
В предыдущих
обозначениях:
a2 b,
a3 c
b1 f ,
b2 g ,
b3 h,
b4 m,
b5 n
8
9.
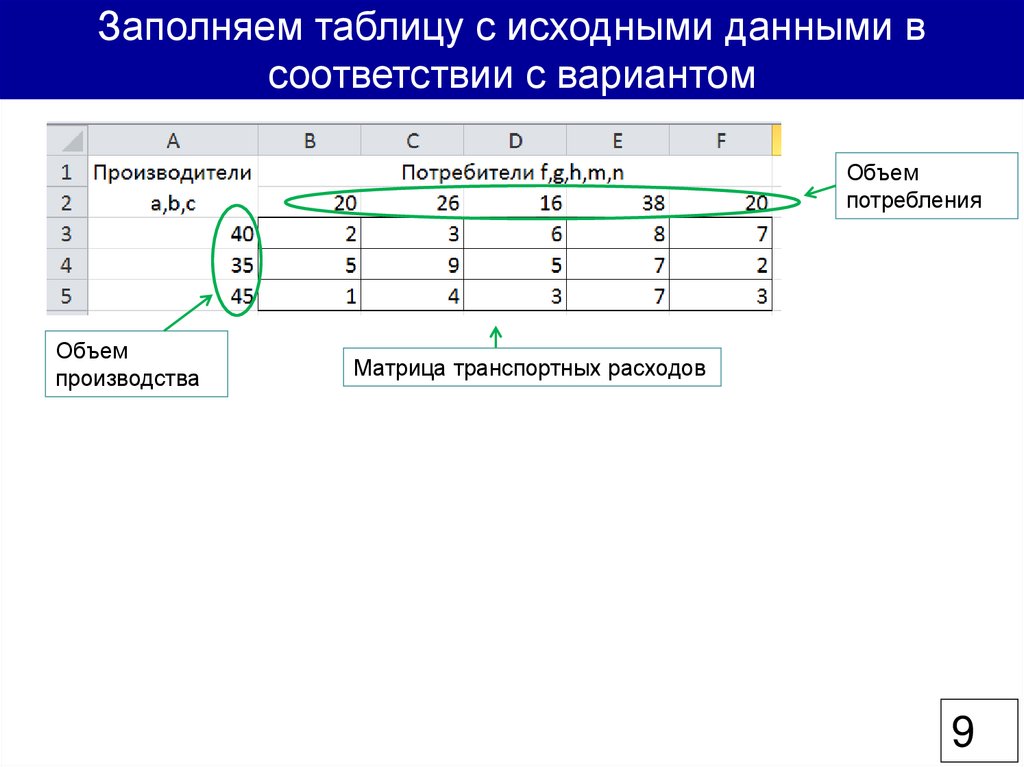
Заполняем таблицу с исходными данными всоответствии с вариантом
Объем
потребления
Объем
производства
Матрица транспортных расходов
9
10.
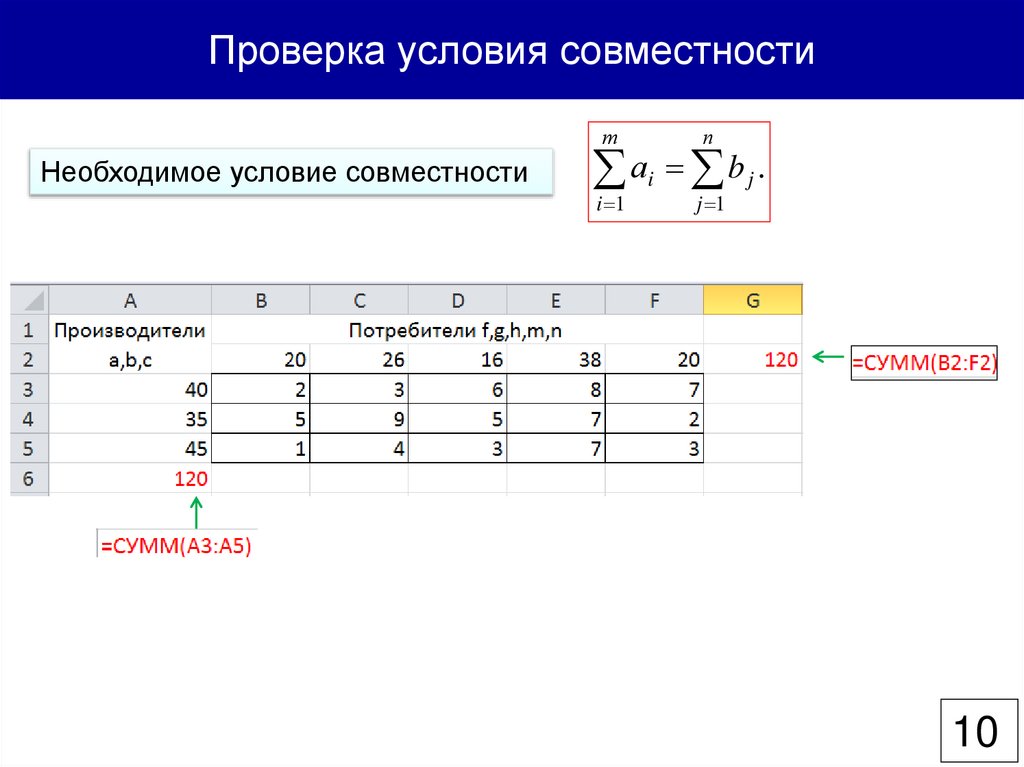
Проверка условия совместностиНеобходимое условие совместности
т
п
i 1
j 1
аi b j .
10
11.
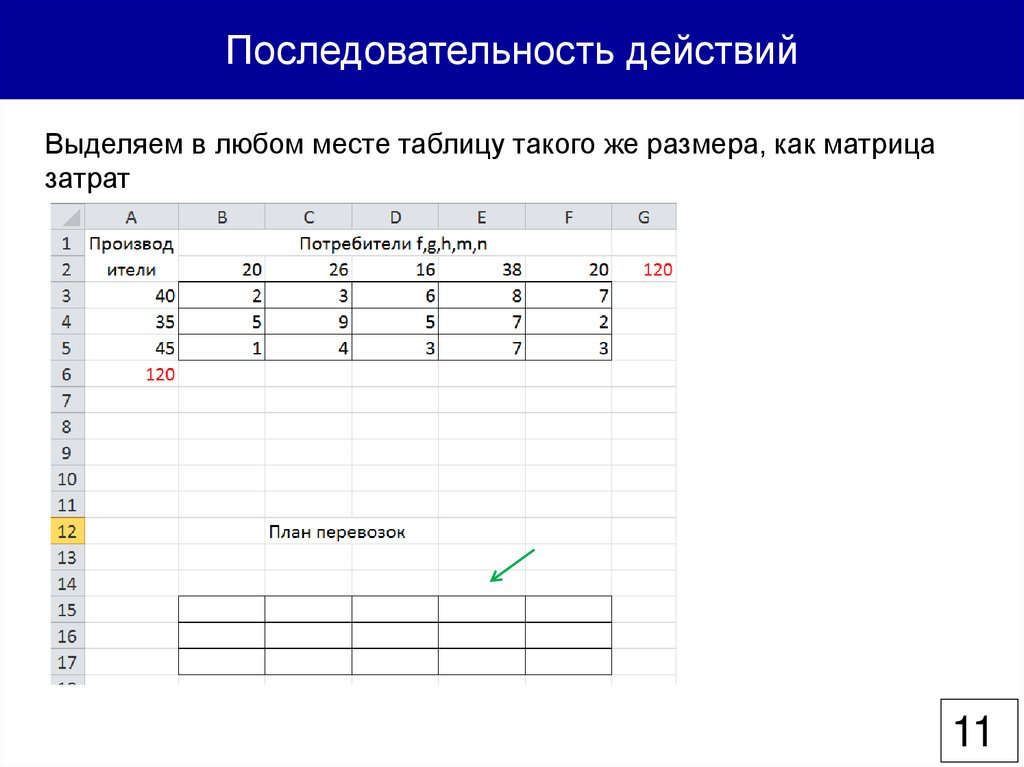
Последовательность действийВыделяем в любом месте таблицу такого же размера, как матрица
затрат
11
12.
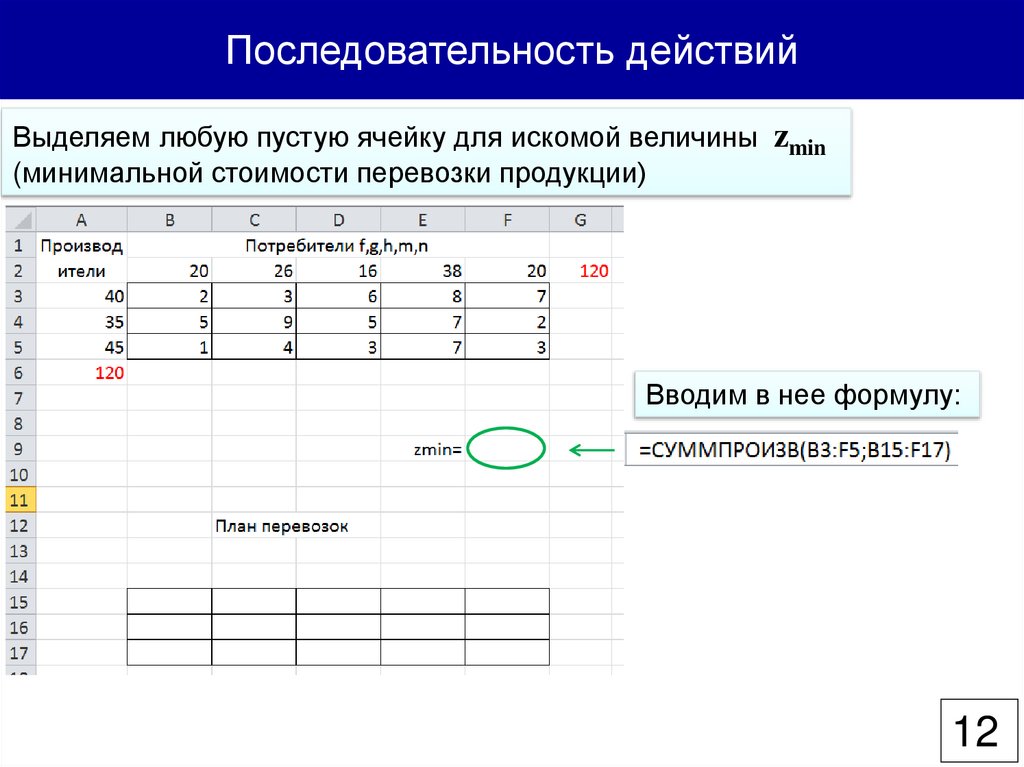
Последовательность действийВыделяем любую пустую ячейку для искомой величины zmin
(минимальной стоимости перевозки продукции)
Вводим в нее формулу:
12
13.
Последовательность действийСтавим курсор на ячейку сверху от верхней левой ячейки
таблицы плана перевозок (ячейка В14)
Вводим в нее формулу:
13
14.
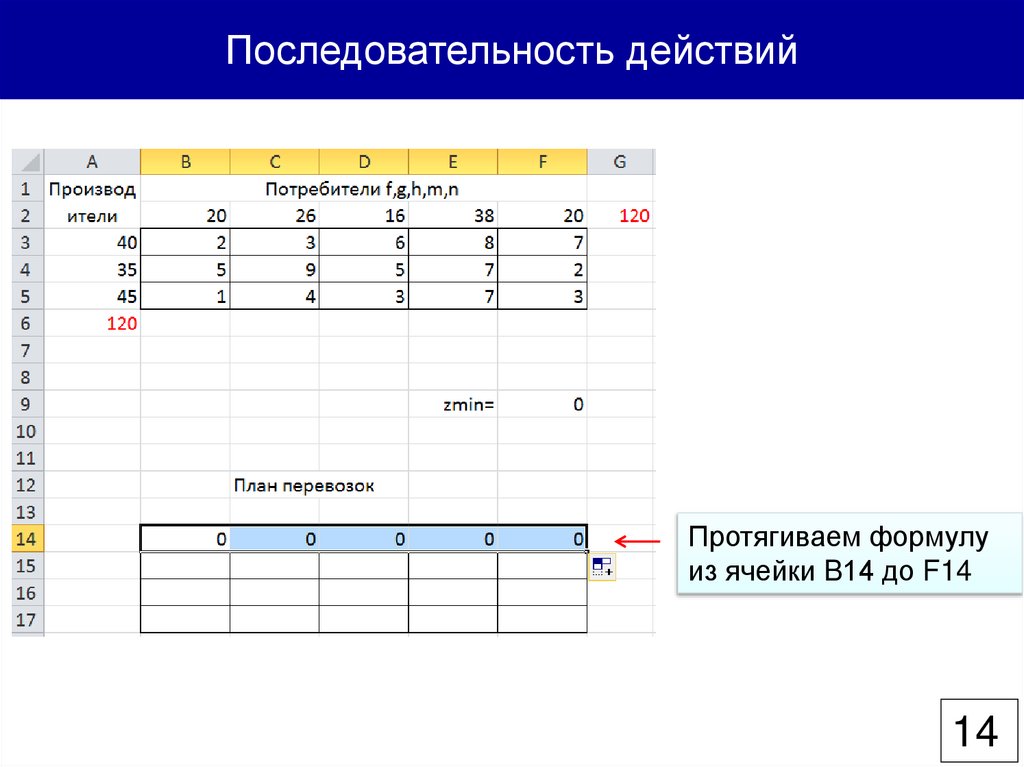
Последовательность действийПротягиваем формулу
из ячейки B14 до F14
14
15.
Последовательность действийСтавим курсор на ячейку слева от верхней левой ячейки
таблицы плана перевозок (ячейка А15)
Вводим в нее формулу:
15
16.
Последовательность действийПротягиваем формулу
из ячейки А15 до А17
16
17.
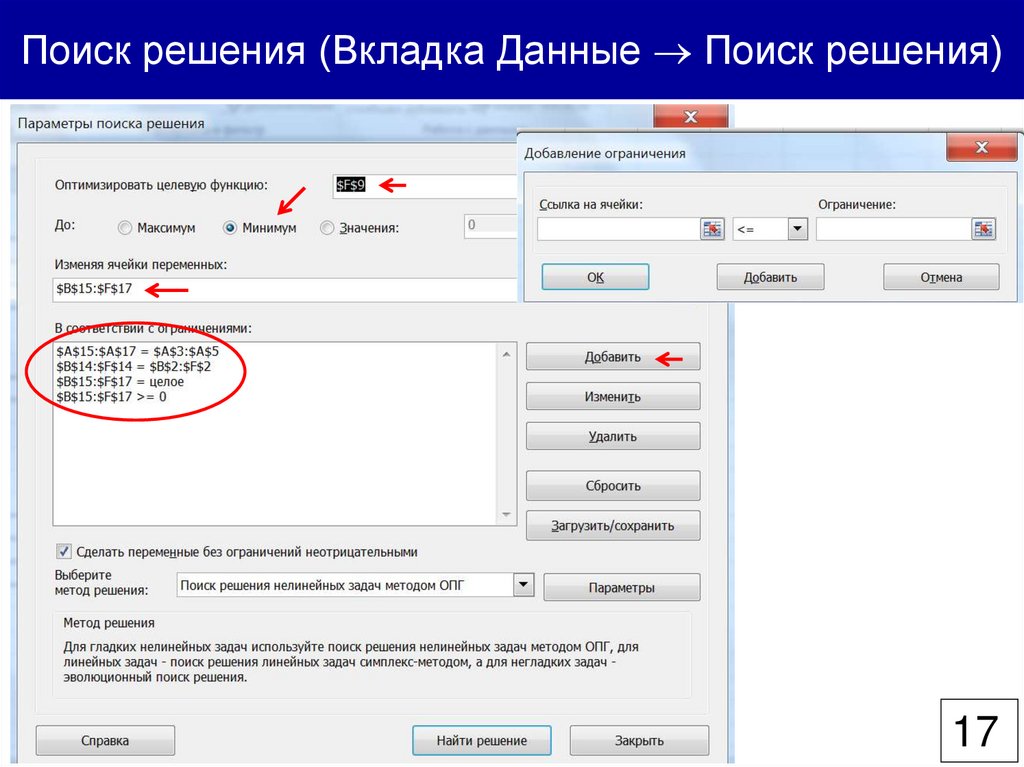
Поиск решения (Вкладка Данные Поиск решения)17
18.
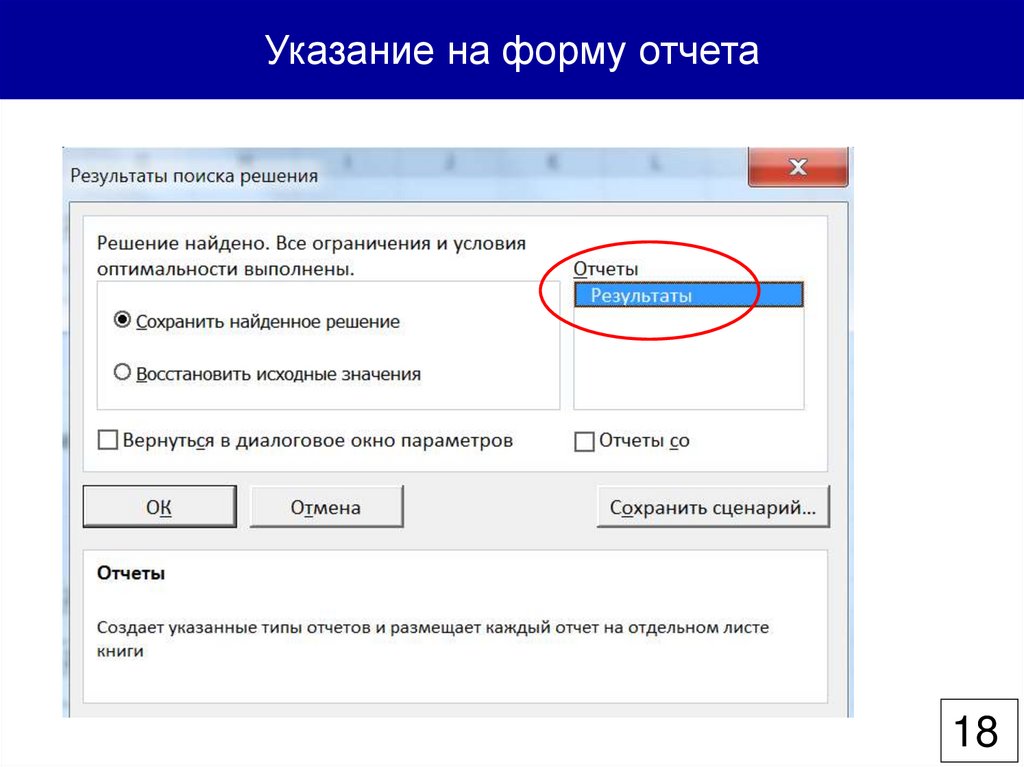
Указание на форму отчета18
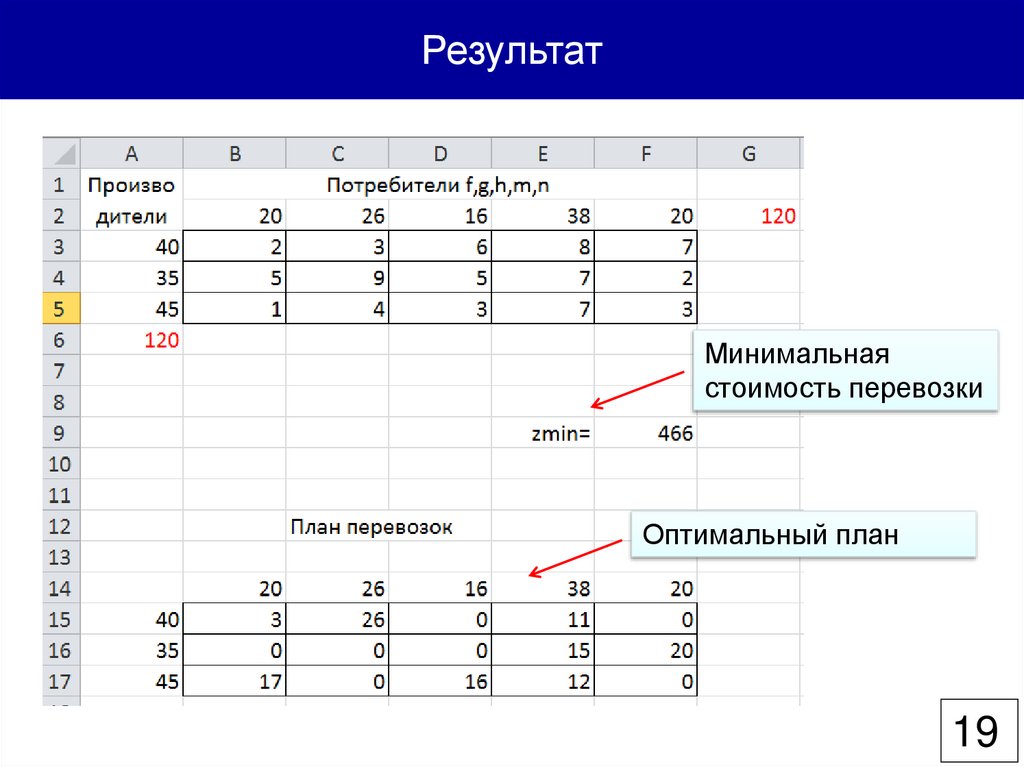
19.
РезультатМинимальная
стоимость перевозки
Оптимальный план
19
20.
Задание для ручного счетаНа основе лекционного материала:
1. составить первоначальный план распределения двумя способами
а) методом наименьшей стоимости
б) методом северо-западного угла
2. Используя метод потенциалов, найти оптимальный план. В
качестве первоначального плана использовать распределение,
полученное методу наименьшей стоимости.
20











 mathematics
mathematics








