Similar presentations:
Сокращение алгебраических дробей
1. Сокращение алгебраических дробей
2.
• Сократить дробь – это значит, разделитьодновременно числитель и знаменатель
дроби на их общий множитель, на одно и
то же отличное от нуля число.
• Обрати внимание!
• Сначала надо разложить на множители
числитель и знаменатель дроби.
3. Алгоритм сокращения алгебраических дробей:
• разложить и числитель, и знаменательдроби на множители;
• разделить одновременно числитель и
знаменатель дроби на их общий множитель
(сократить).
4. Запомним !
• Переменные (буквы), входящие валгебраическую дробь, могут принимать
лишь допустимые значения, то есть такие
значения, при которых
5а −6
а+2
• Пример: для дроби
допустимы все
значения а, кроме а = - 2
5.
Для дробиa
допустимыми
a a 1
являются все значения а, кроме а = 0 и а = 1.
6. Сократите дробь
х2 − 6х + 5х−5
1) Разложим квадратный трехчлен х2 − 6х +
5 на множители
х2 − 6х + 5=0
Корни 1 и 5, коэффициент а = 1, значит
х2 − 6х + 5 = 1(х − 1)(х − 5)
7.
х2 − 6х + 5 (х − 1)(х − 5)=
=х−1
х−5
х−5
Можно сократить на общий множитель (х-5)
Ответ: х - 1
8. Пример 2
Сократить дробьх2 +9х+14
х2 +7х
1) Разложить числитель на множители
Корни -7 и -2 , коэффициент а=1, пользуясь
флрмулой
х2 + 9х + 14 = (х + 7)(х + 2)
2) Разложить знаменатель на множители, с
помощью вынесения общего множителя за
скобки
х2 + 7х = х(х + 7)
9.
3)х2 +9х+14
х2 +7х
=
(х+7)(х+2)
х(х+7)
=
х+2
2
Разделим на общий множитель (х+7)
Ответ:
х+2
2






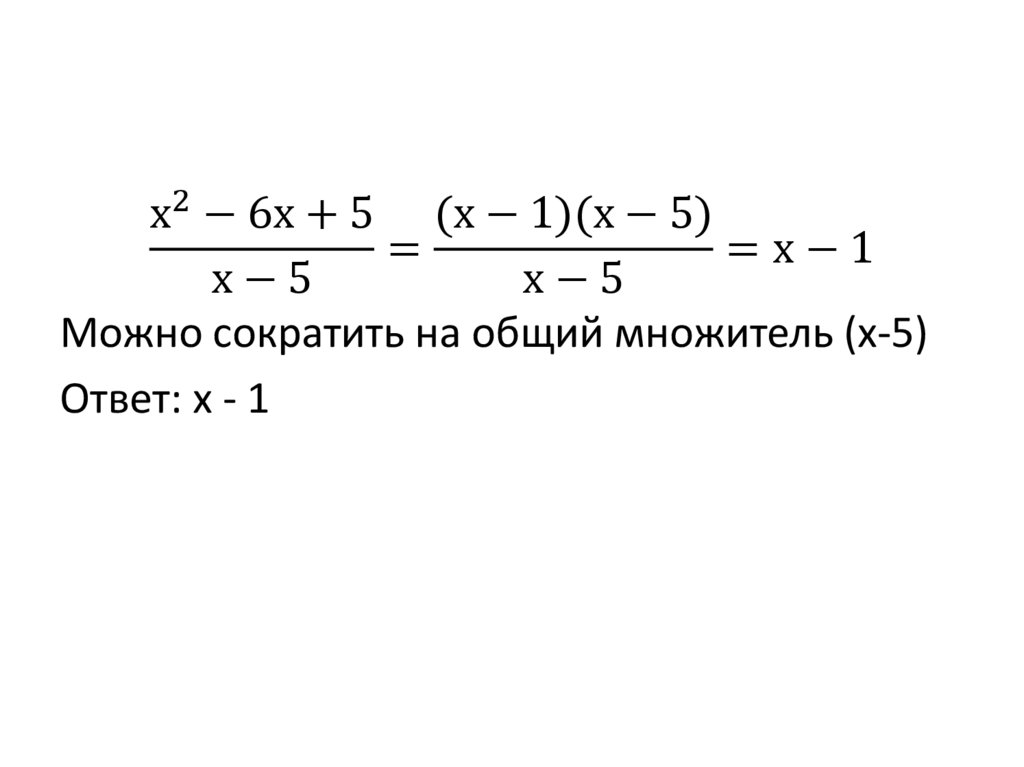


 mathematics
mathematics








