Дискретные источники

1. Информатика

Лекция 3
Дискретные источники

2. Дискретные источники без памяти

Дискретный источник без памяти (ДИБП)
полностью задается таблицей распределения
вероятностей:
x1 x2 xN
X
p1 p2 p N
N
Информационные
характеристики ДИБП:
Энтропия H ( X ) pi log pi ; максимальная энтропия H max log N ;
i 1
Избыточность D H max H ( X ) ;
D
H max H ( X )
Относительная избыточность D0
;
H max
H max
N
Средняя длительность выдачи одного символа cp pi i ;
i 1
Производительность источника I ( X )
H (X )
cp
.

3. Дискретные источники с памятью

Дискретный источник с памятью r и алфавитом x1 , x2 , xN задается множеством состояний S1 , S 2 , S M , M N r ; вероятностями p ( j ) (i) появления символа xi в состоянии S j ; графом перехода из состояния S [n]
( x[n r ], x[n r 1] x[n 1]) в S[n 1] ( x[n r 1], x[n r 2] x[n])
после появления очередного символа x[n] ; начальным распределением
состояний p 0 ( p0 (1), p0 (2) p0 ( M )) .
Будем предполагать стационарность (независимость от начала отсчета
времени) и эргодичность (однотипность всех возможных последовательностей символов). Любой стационарный источник можно представить как
несколько эргодических источников, различающихся режимами работы.
Совместные энтропии возрастающих последовательностей символов:
H ( X 1 X 2 ) , H ( X 1 X 2 X 3 ) , дают в среднем на один символ энтропию
1
H L ( X ) H ( X1 X 2 X L ) .
L
Условная энтропия L -го символа H ( X L | X 1 X 2 X L 1 ) .
Теорема. lim H ( X L | X 1 X 2 X L 1 ) lim H L ( X ) H ( X ) .
L
L

4. Цепи Маркова

Математической моделью ДИСП является цепь Маркова. Это
последовательность состояний S [1], S [2], , S [n], , каждое из
которых принадлежит множеству S1 , S 2 , S M , и заданные
вероятности перехода n2 n1 ( j2 | j1 ) P( S [n2 ] S j 2 | S[n1 ] S j1 ) .
Они должны удовлетворять следующим свойствам:
M
1. n 2 n1 ( j2 | j1 ) 1 (полная группа);
j 2 1
M
2. n3 n1 ( j3 | j1 ) n3 n2 ( j3 | j2 ) n 2 n1 ( j2 | j1 ) (равенство
j 2 1
Колмогорова-Чэпмена).

5.

Для стационарного ДИСП (независимого от начала отсчета
времени) достаточно задать
n1 l , n1 ( j2 | j1 ) P( S [n1 l ] S j 2 | S [n1 ] S j1 ) , то есть матрицу
n 1, n (2 | 1) n 1, n ( M | 1)
n 1, n (1 | 1)
n 1, n (1 | 2) n 1, n (2 | 2) n 1, n ( M | 2)
,
n 1, n (1 | M ) n 1, n (2 | M ) n 1, n ( M | M )
тогда по равенству Колмогорова-Чэпмена,
p n ( pn (1), pn (2) pn ( M )) p 0 n , где p 0 ( p0 (1), p0 (2) p0 ( M )) .
Из эргодичности ДИСП следует регулярность цепи Маркова, т.е.
существование предела lim n . Тогда все строки матрицы
n
равны предельному распределению p ( p (1), p (2) p ( M )) ,
являющемуся собственным вектором: p p .
M
Энтропия в этом случае равна H ( X ) p ( j ) H ( X | S j ) , где
j 1
N
H ( X | S j ) p ( j ) (i ) log p ( j ) (i ) .
i 1

6.

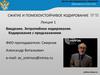
Пример. Двоичный источник имеет память r 2 и вероятности
появления символов для каждого состояния даны в таблице:
0
1
0
1
S1 (00)
S 2 (11)
1
1
0
1
p (1)
p ( 2)
2
2
0
1
0
1
S3 (01)
S 4 (10)
2
1
3
1
p (3)
p ( 4)
3
3
4
4
Граф состояний:
1
Матрица переходных
S1 (00)
S2 (11)
вероятностей:
0
0 0 1 0
1
1
1
0
0
0
2
2
1
2
Π
1
0
0
0
3
3
1
S3 (01)
S 4 (10)
3
1
0
0
4
4
0

7.

9 8 12 12
1 9 8 12 12
n
Предельная матрица lim
, значит
n
41 9 8 12 12
9 8 12 12
8 12 12
9
p
. Энтропии для каждого состояния:
41 41 41 41
H ( X | S1 ) 0 ; H ( X | S 2 ) 1; H ( X | S3 ) 0,918 ; H ( X | S 4 ) 0,811.
Энтропия всего источника
9
8
12
12
H ( X ) 0 1 0,918 0,811 0,701.
41
41
41
41
Если не принимать во внимание различие состояний, то есть
считать этот источник источником без памяти, то
9 1 8 2 12 3 12 21
P (0) 0 ;
41 2 41 3 41 4 41 41
9 1 8 1 12 1 12 20
и H ( X ) 0,999 .
P (1) 1
41 2 41 3 41 4 41 41

8. Информационные характеристики ДИСП:

M
Объем памяти r ; Энтропия H ( X ) p ( j ) H ( X | S j ) ;
j 1
Максимальная энтропия H max log N ;
Избыточность D H max H ( X ) ;
D
H max H ( X )
Относительная избыточность D0
;
H max
H max
N
Средняя длительность выдачи одного символа cp pi i ,
i 1
M
где pi p ( j ) p ( j ) (i ) ;
j 1
Производительность источника I ( X )
H (X )
cp
.