Преобразование чертежа. Вращение

1. ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА. ВРАЩЕНИЕ

Уласевич З.Н., Уласевич В.П., Якубовская О.А.
Начертательная геометрия в слайдах компьютерной среды Microsoft PowerPoint

2. Сущность вращения

Сущность способа вращения заключается в том, что
проецируемая фигура перемещается в пространстве так,
чтобы она заняла частное положение относительно
плоскостей проекций, которые при этом не меняют своего
положения в пространстве.
Выделяют следующие способы вращения:
вращение вокруг проецирующих прямых;
вращение вокруг линий уровня;
вращение вокруг следа (способ совмещения);
плоскопараллельное перемещение;

3.

Это перемещение осуществляется вокруг неподвижной
прямой (ось вращения) в плоскостях, -ых оси вращения
(плоскости вращения).
Каждая точка перемещается по окружности, центр
которой находится в точке пересечения оси вращения с
плоскостью вращения (центр вращения), а радиус равен
расстоянию от центра до вращаемой точки (радиус
вращения).
Если какая-либо точка принадлежит оси вращения, то
при вращении она останется неподвижной.
На чертеже радиус вращения R должен быть в
натуральную величину.

4.

Аппарат вращения:
(геометрические элементы вращения):
1. Точка А (А1, А2) – объект вращения;
2. i (i1, i2) – ось вращения;
3. – плоскость вращения точки А; i;
(параметры вращения):
4. О (О1, О2) – центр вращения i = О;
5. R (R1, R2) – радиус вращения точки А;
R=OA.

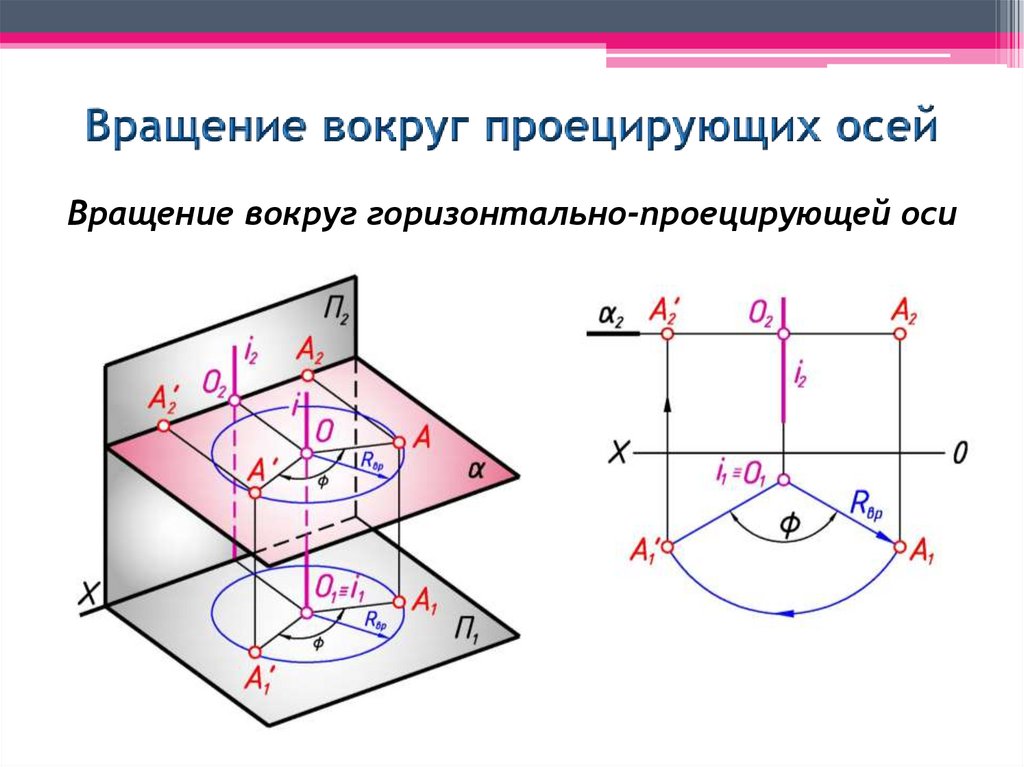
5. Вращение вокруг проецирующих осей

Вращение вокруг горизонтально-проецирующей оси

6.

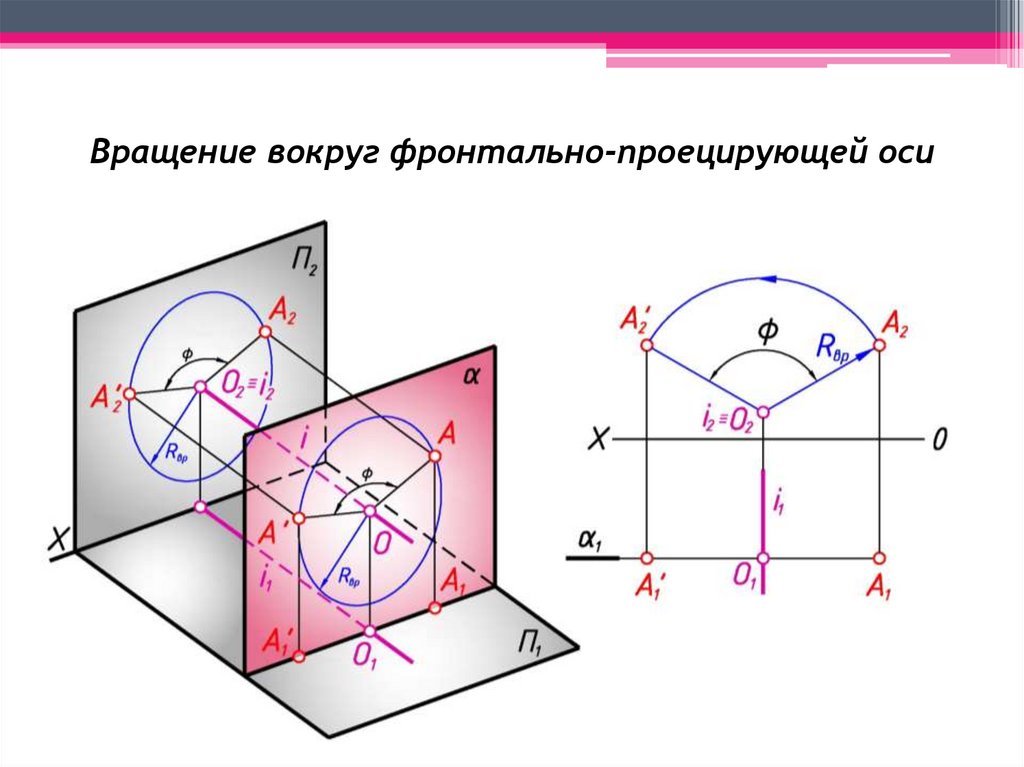
Вращение вокруг фронтально-проецирующей оси

7.

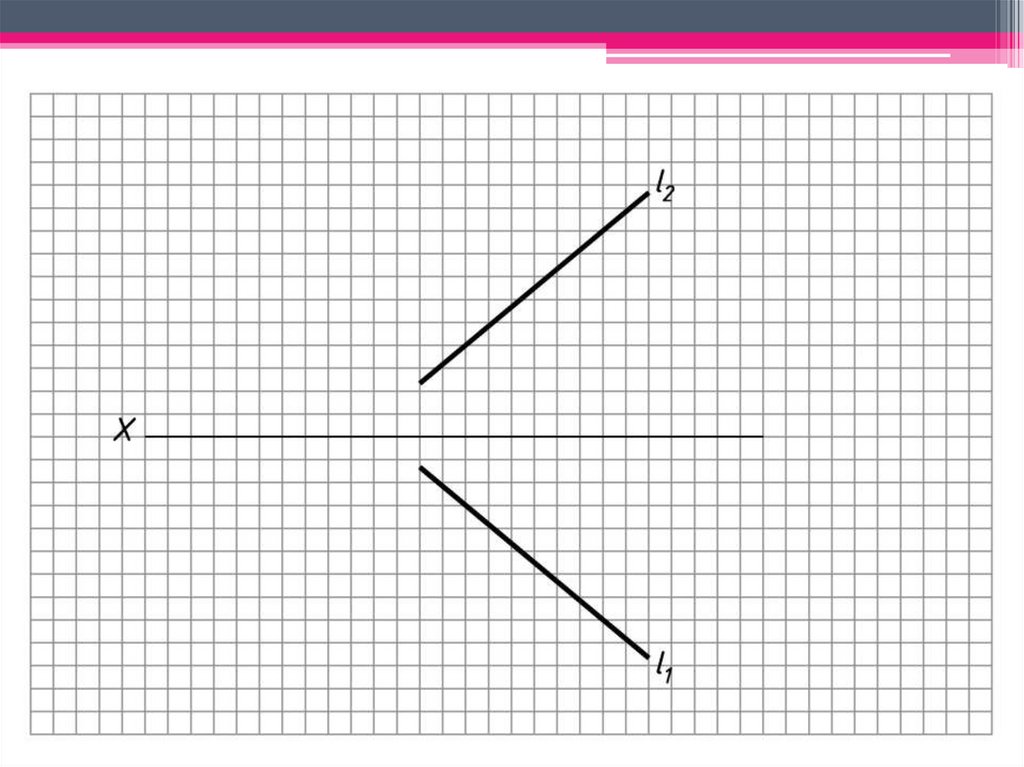
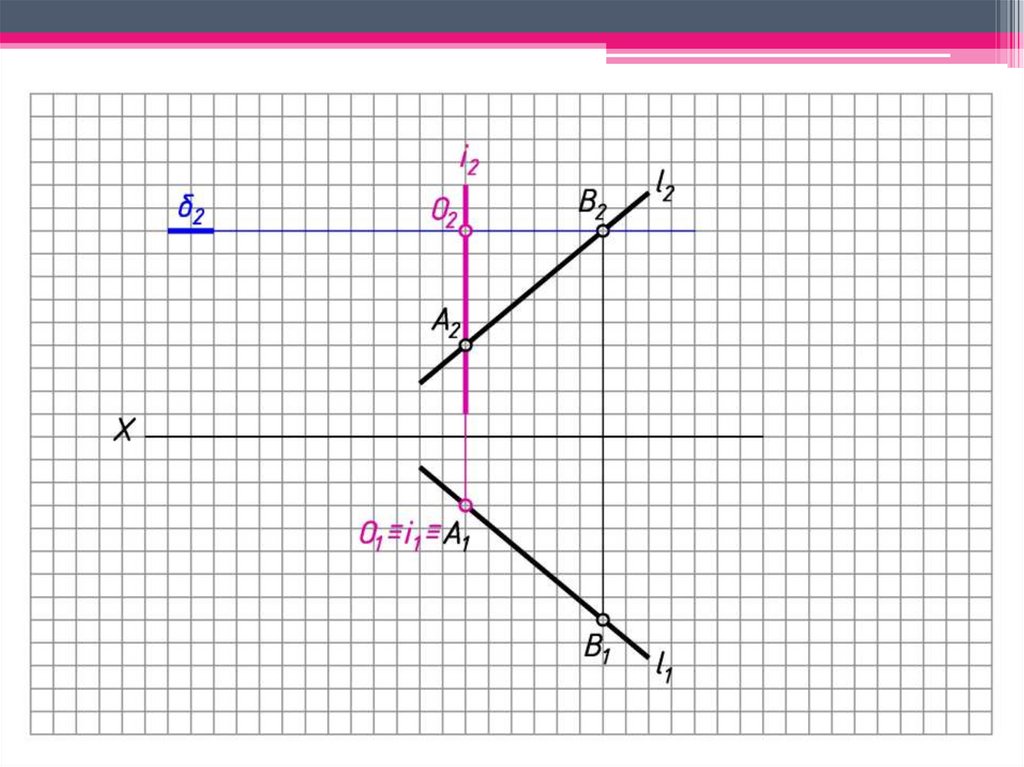
ЗАДАЧА 2: Преобразовать прямую l общего
положения в прямую фронтального уровня, найти
угол наклона l к 1 .
Алгоритм решения:
1. Выбираем 2 произвольные точки на прямой l (A, B
l).
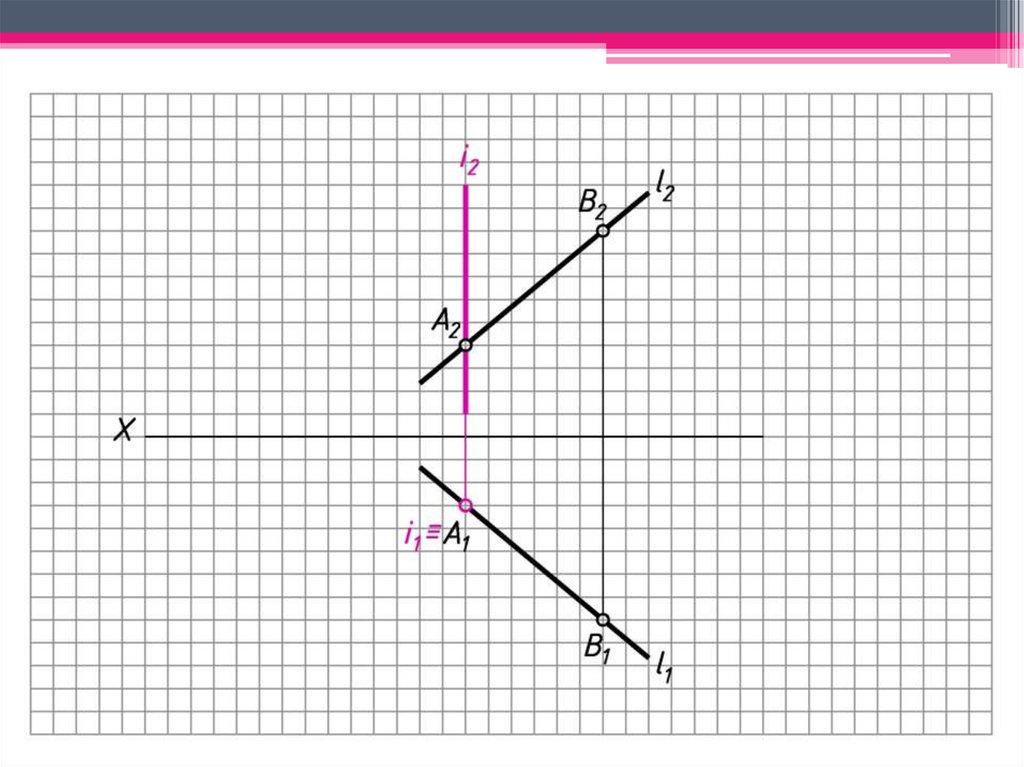
2. Ч/з т. А проводим i 1, где i – ось вращения.
3. При вращении т. А останется неподвижной, т.к. А
i.
4. Ч/з В2 проводим след плоскости вращения т. В - 2
( 2 i2).
5. i2 ∩ 2 = O2 – центр вращения т. В; O1 ≡ i1.
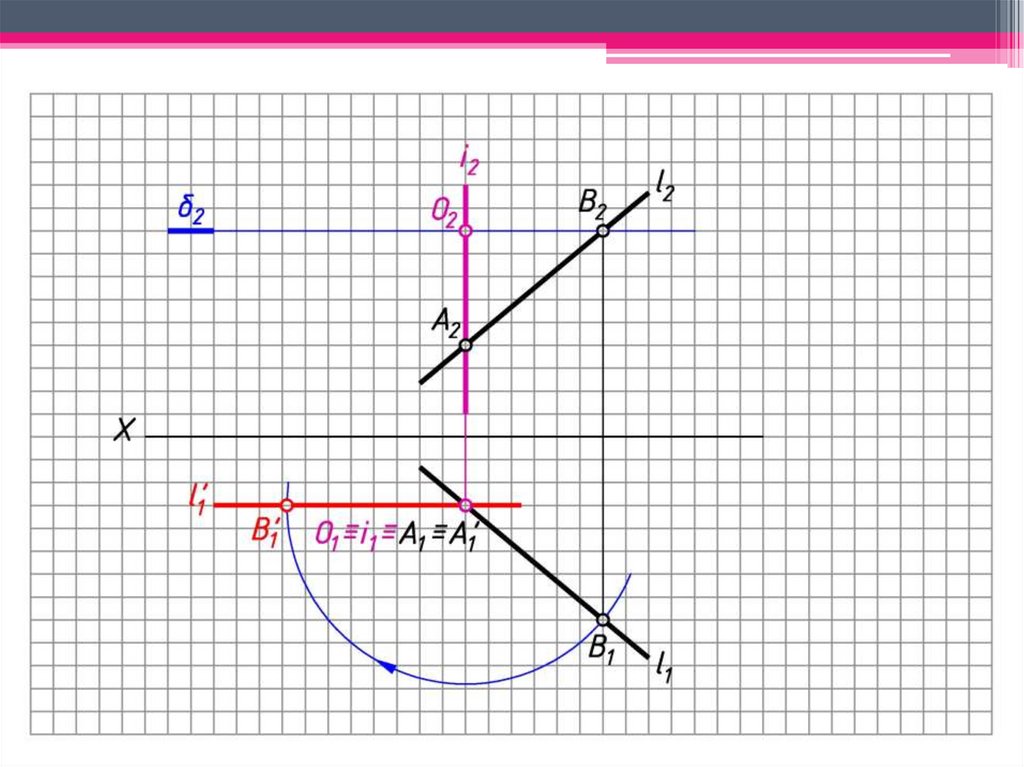
6. Вращаем l1 до положения l’1 Х.
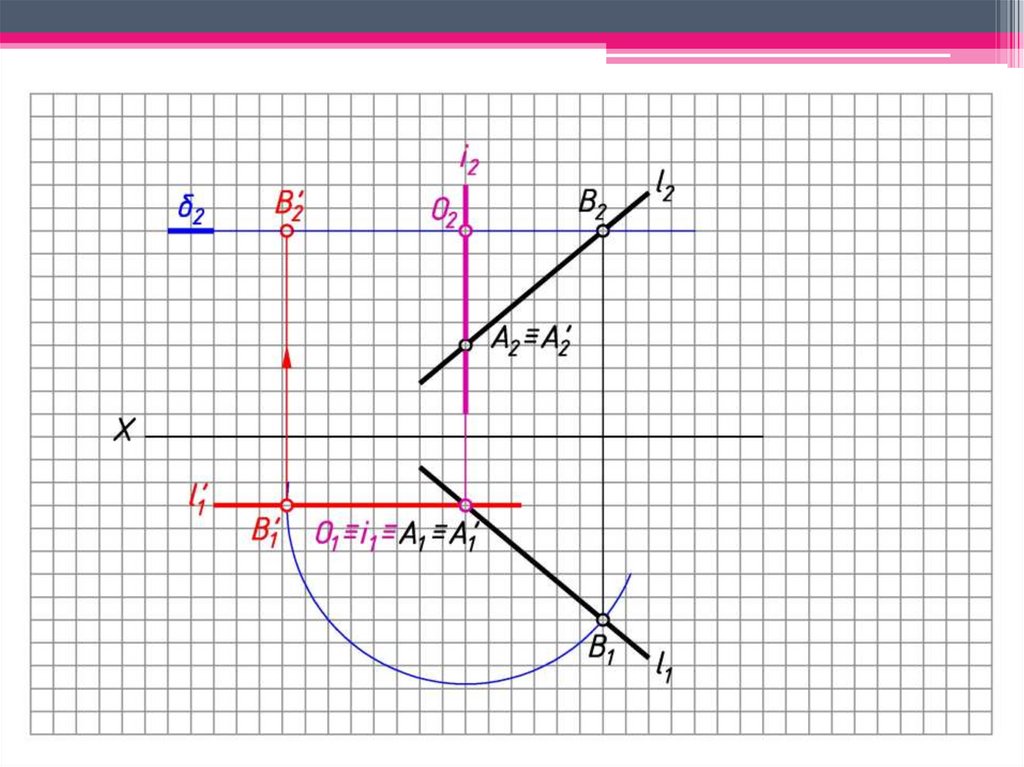
7. В’2 2.
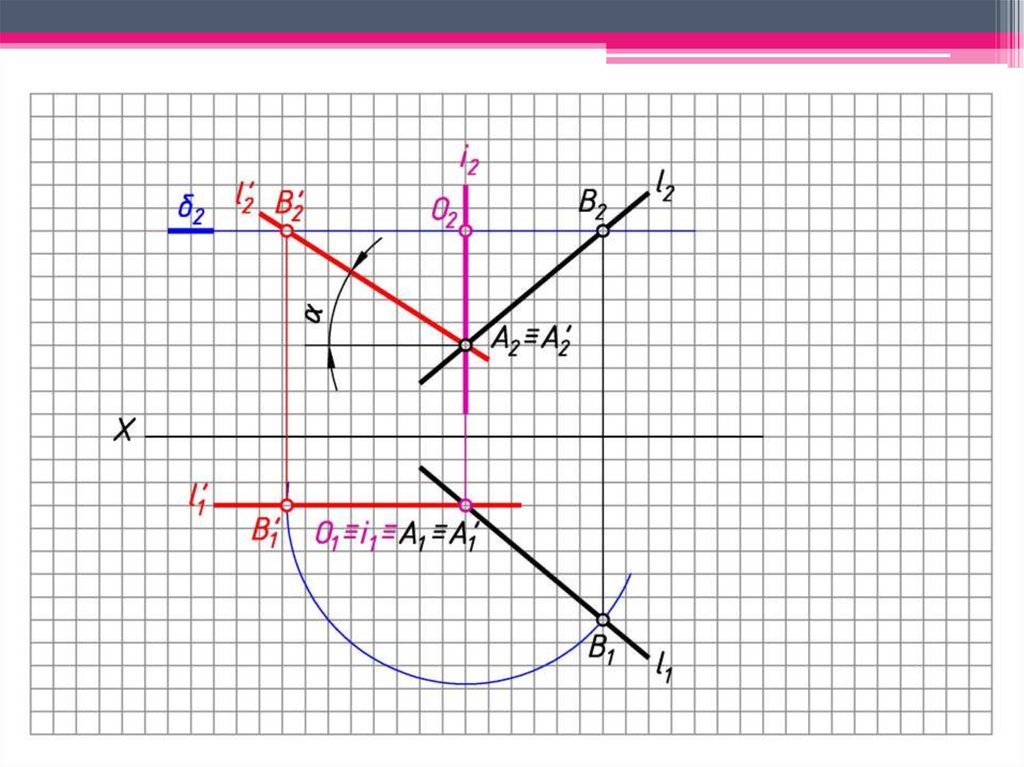
8. Прямая l’ – фронтального уровня; - угол наклона
l к 1,

8.

9.

10.

11.

12.

13.

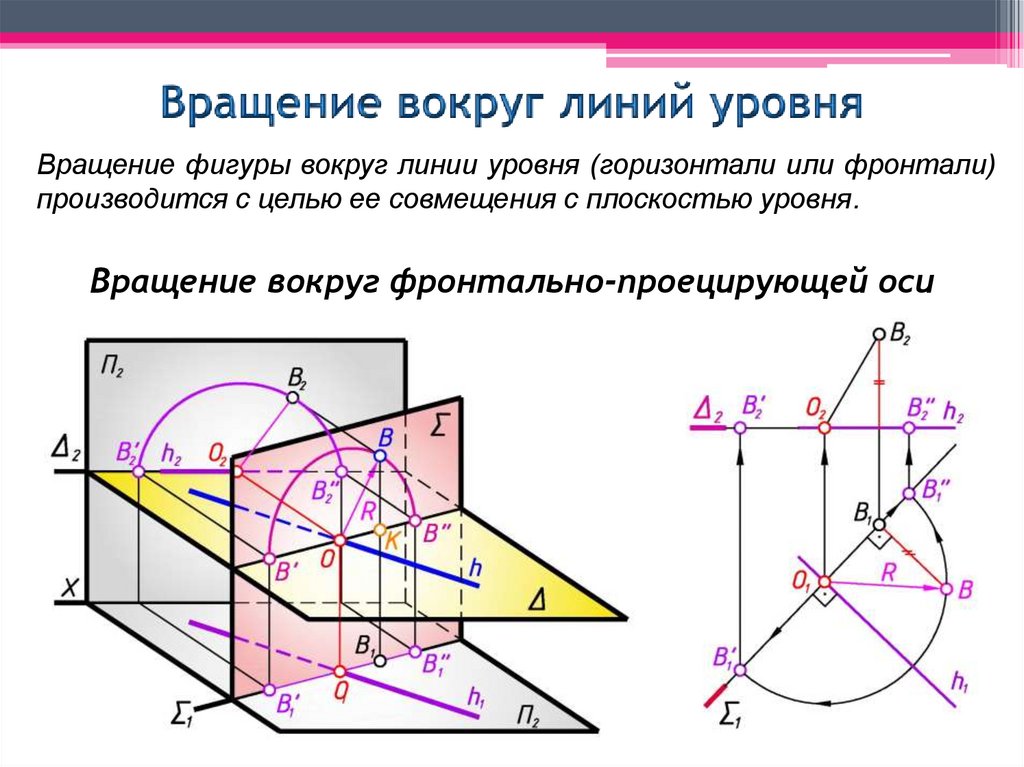
14. Вращение вокруг линий уровня

Вращение фигуры вокруг линии уровня (горизонтали или фронтали)
производится с целью ее совмещения с плоскостью уровня.
Вращение вокруг фронтально-проецирующей оси

15.

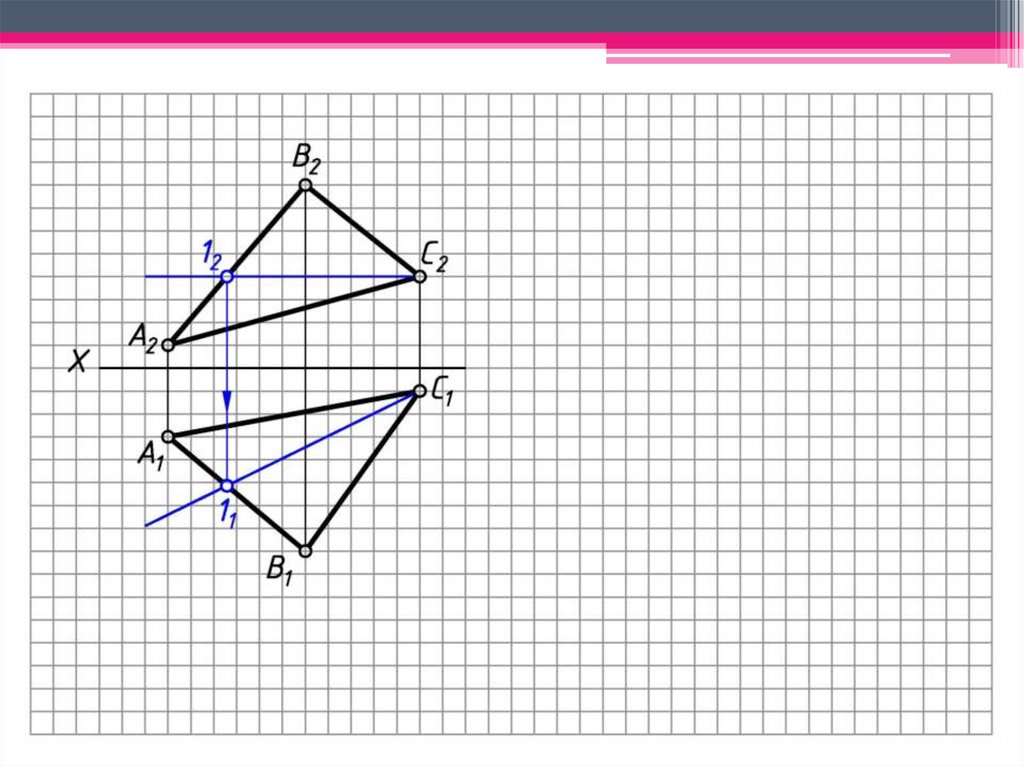
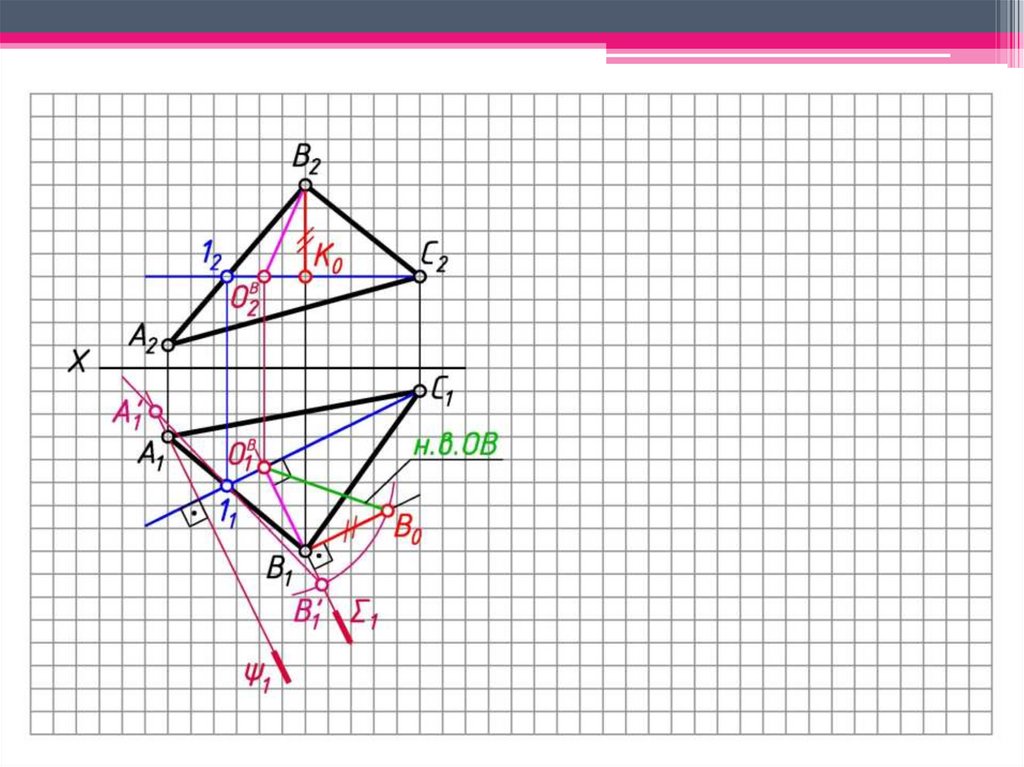
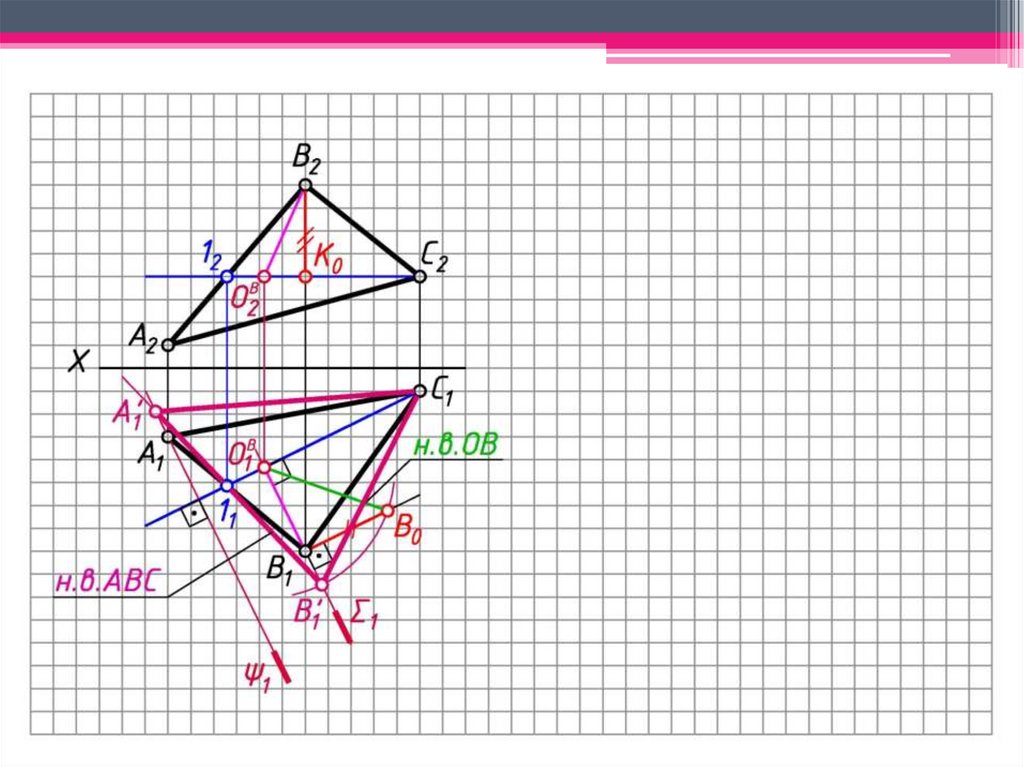
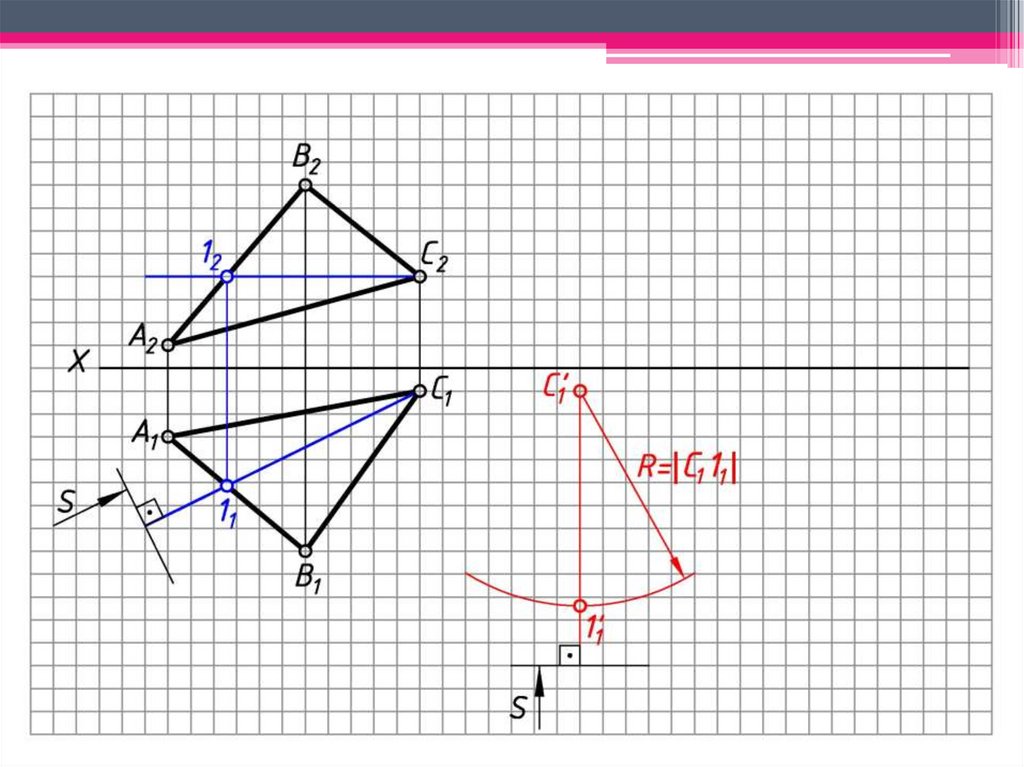
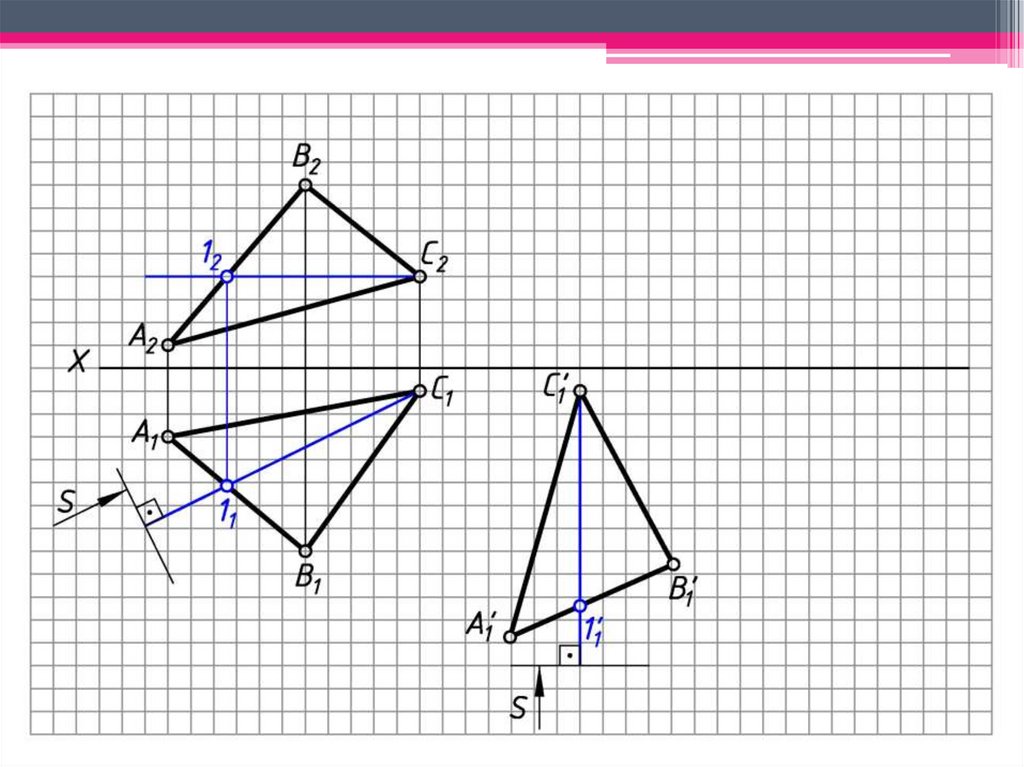
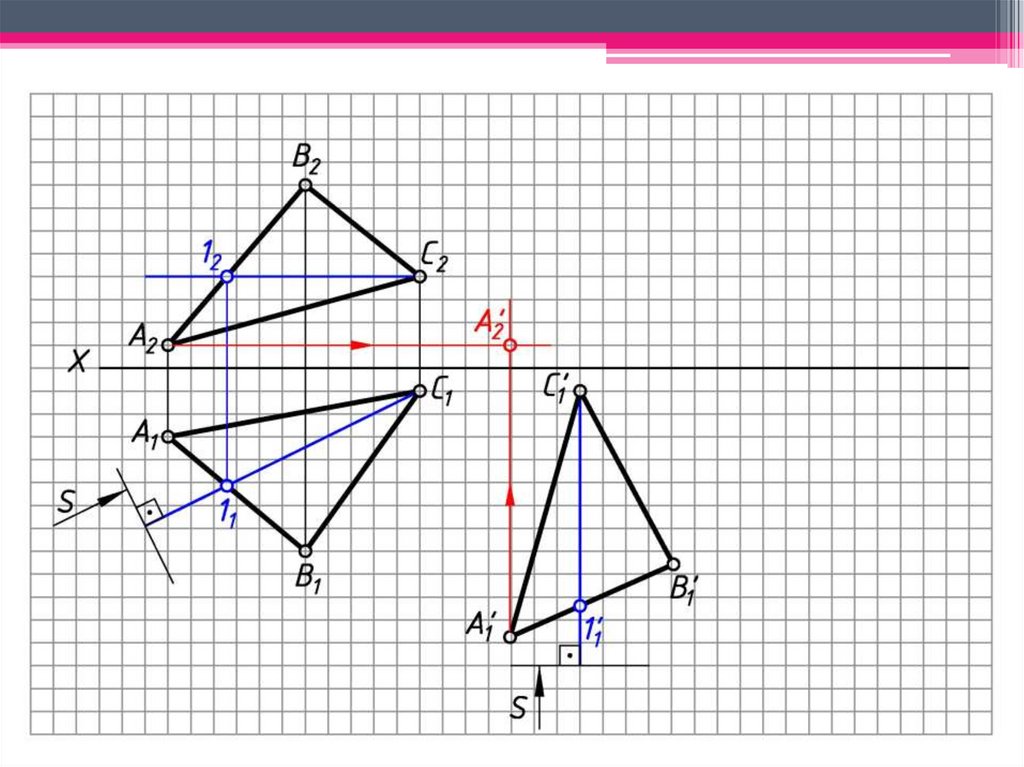
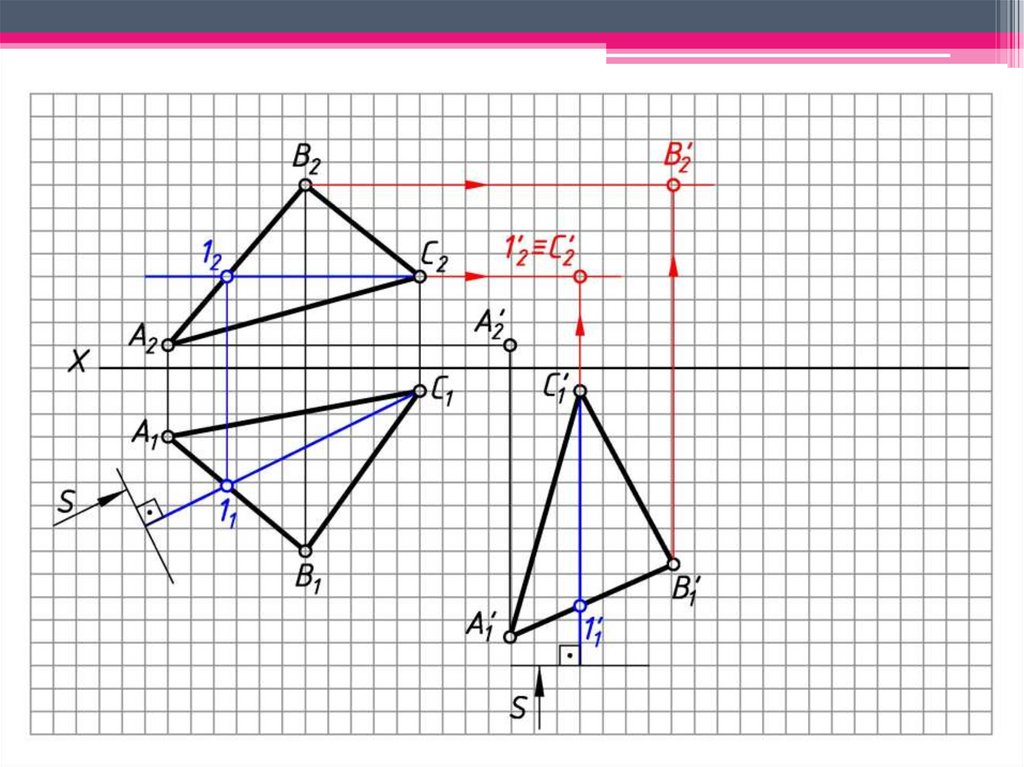
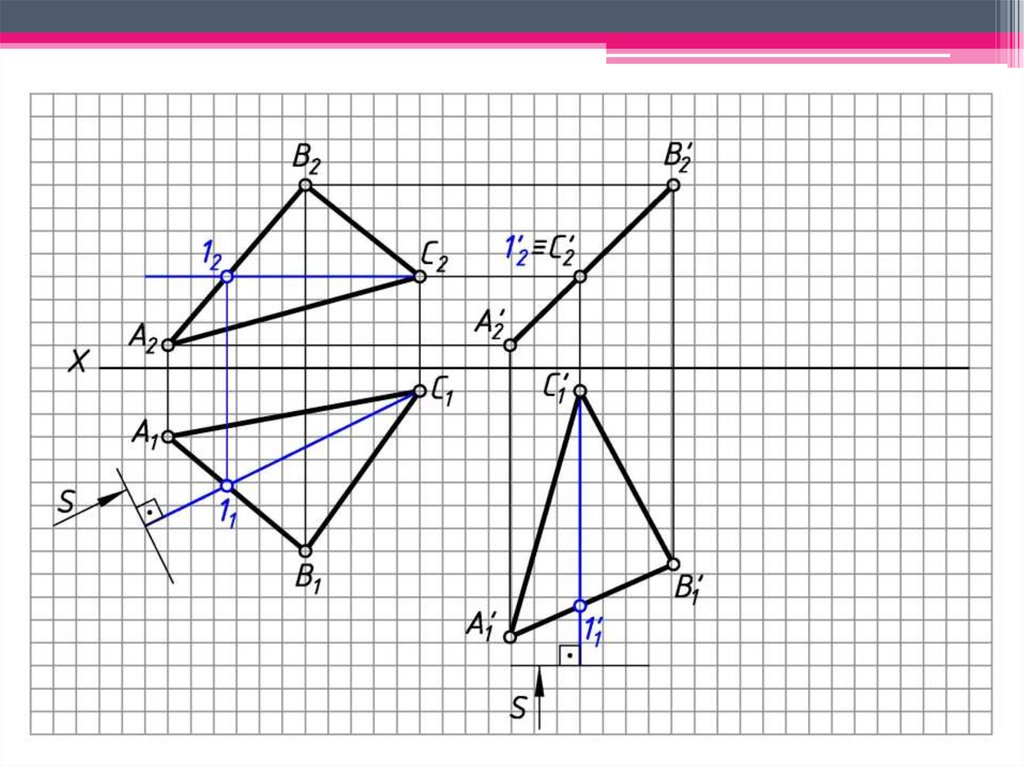
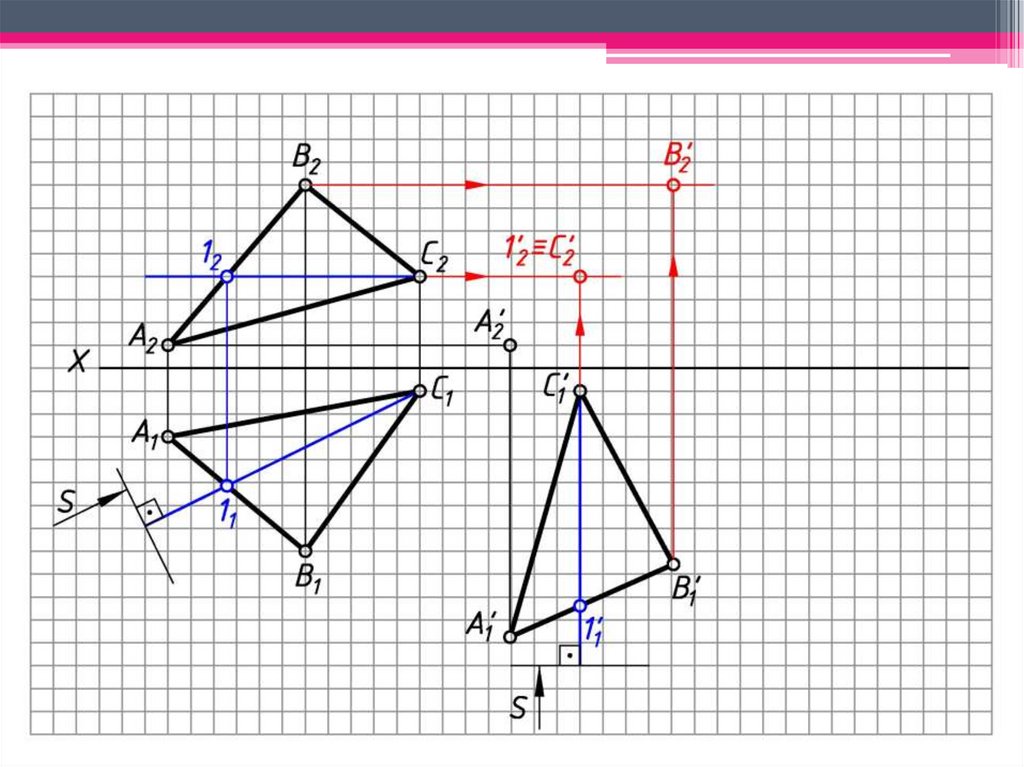
ЗАДАЧА 3: Определить н.в. ΔАВС способом вращения
вокруг линии уровня.
Алгоритм решения:
1. Построим горизонталь С1 (С111; С212) – ось
вращения.
2. С оси вращения при вращении т. С остается
неподвижной.
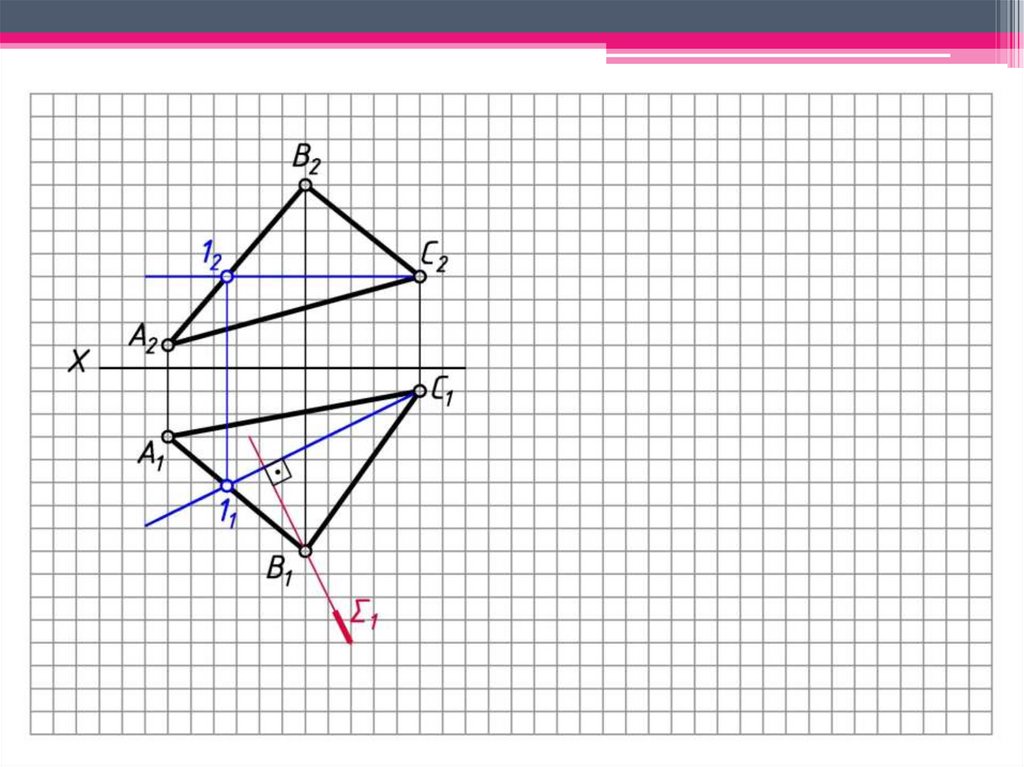
3. 1 С111 – след плоскости вращения т. В.
4. 1 ∩ С111 = ОВ1; ОВ1 С212 – центр вращения т. В.
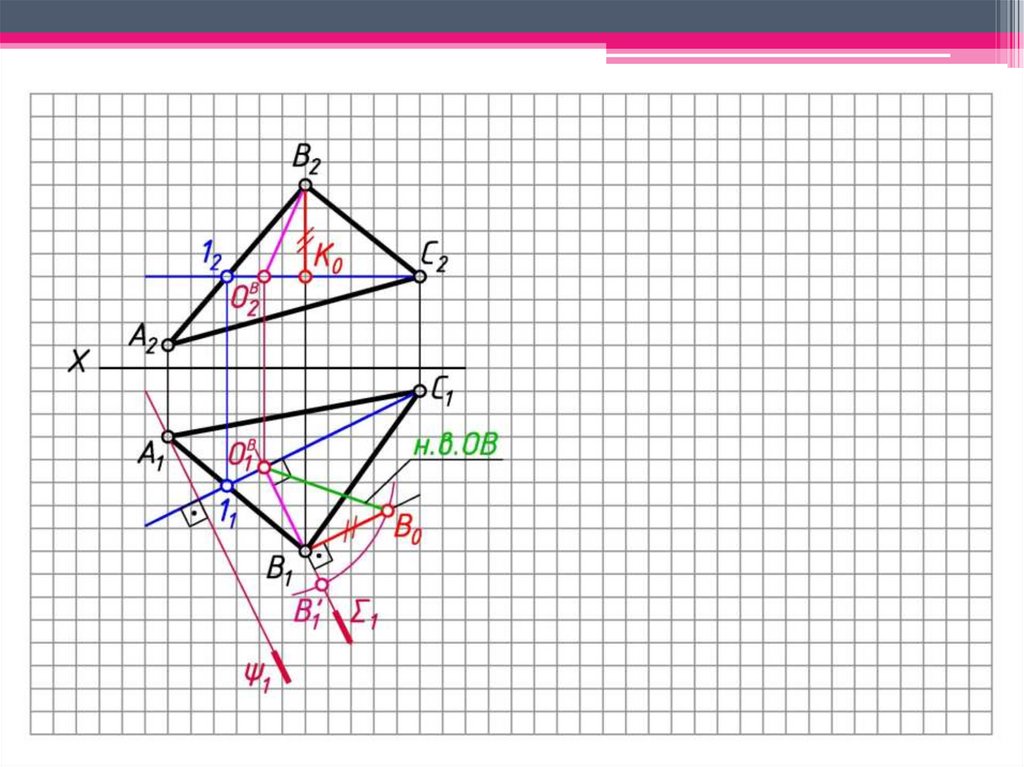
5. ОВВ (ОВ1В1; ОВ2В2) - радиус вращения т. В.
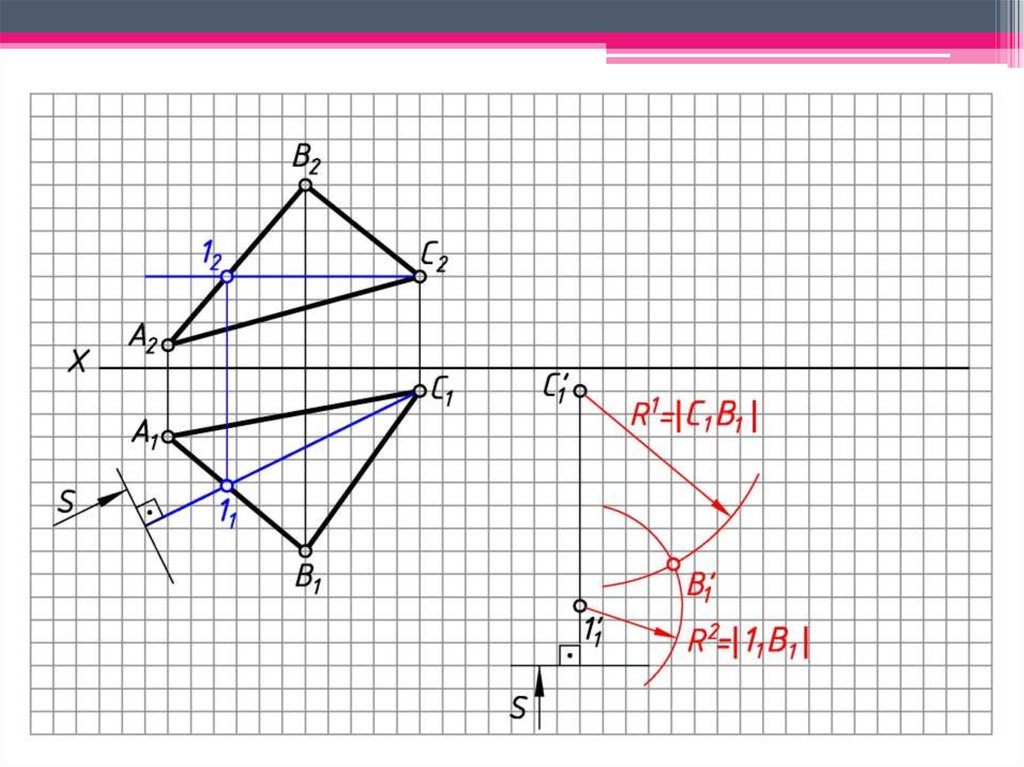
6. Определяем н.в. ОВВ способом прямоугольного
треугольника
ОВ1В0 – н.в. ОВВ.
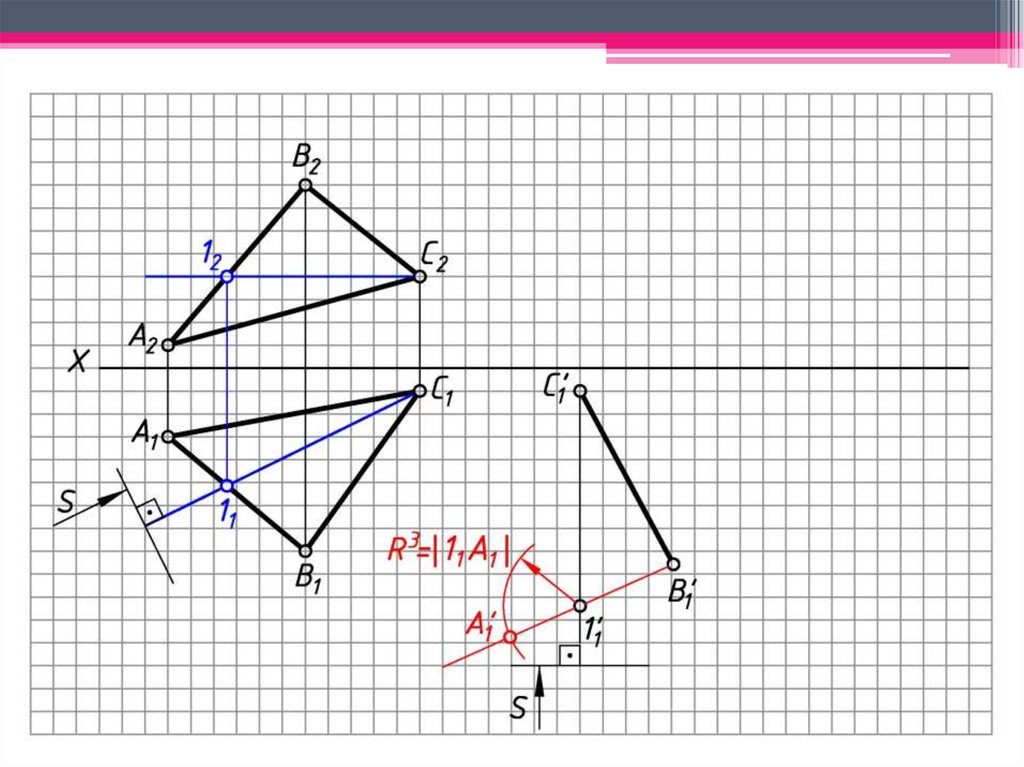
7. Окр. (ц. ОВ1; R = ОВ1В0 ) ∩ 1 = B’1.
8. 1 С111 – след плоскости вращения т. А.
9. 1 оси вращения при вращении т. 1 остается
неподвижной.

16.

17.

18.

19.

20.

21.

22.

23.

24.

25. Вращение вокруг следа (совмещение)

Совмещение (вращение вокруг следа пл-ти) – это
частный случай вращения вокруг горизонтали, или
фронтали, т.к. следы пл-ти – это нулевые
горизонтали и фронтали.
Если вращение происходит вокруг гор. следа, то
пл-ть
совмещается
с
1.
Если
вращение
осуществляется вокруг фронт. следа, то пл-ть
совмещается с 2.

26.

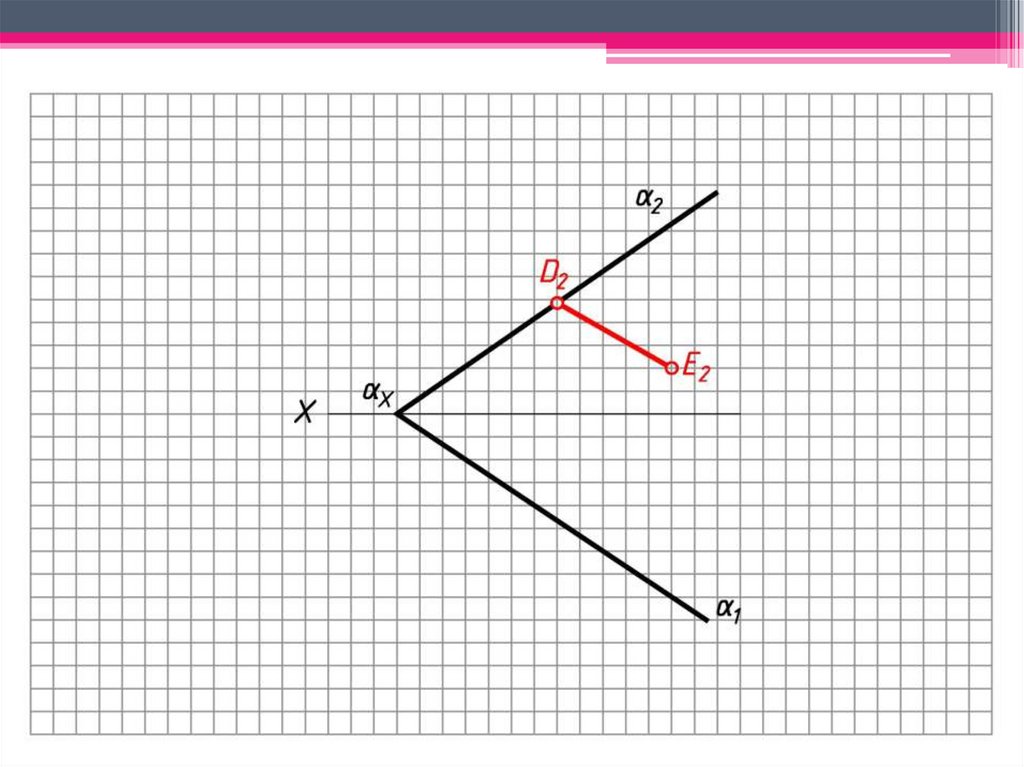
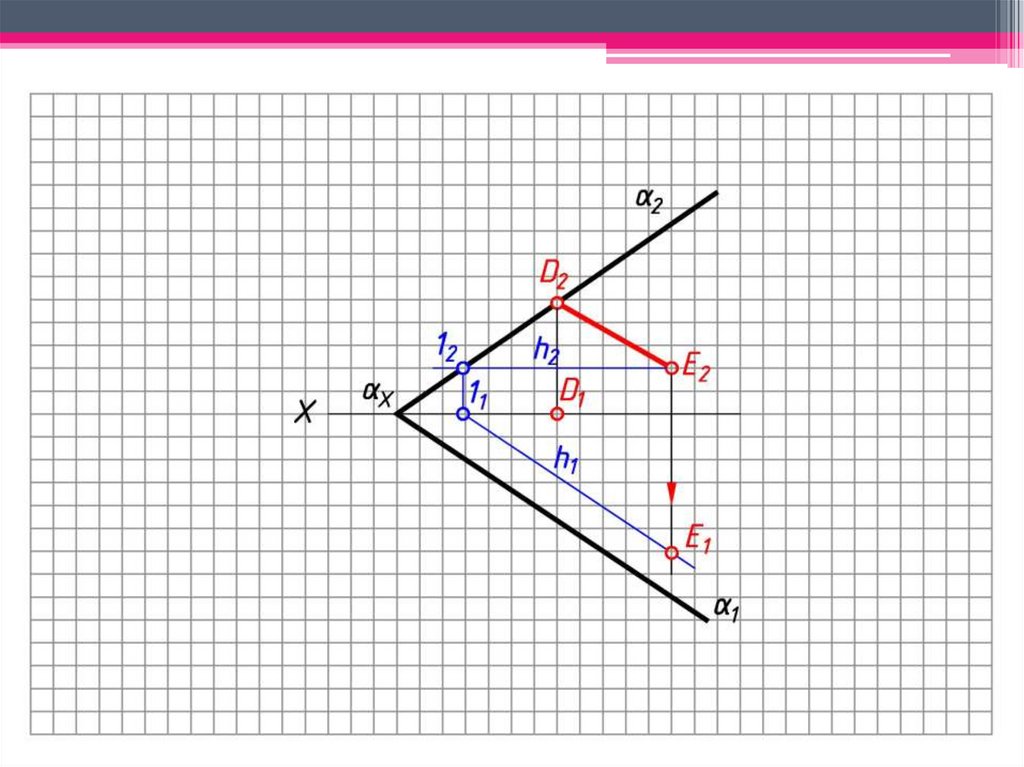
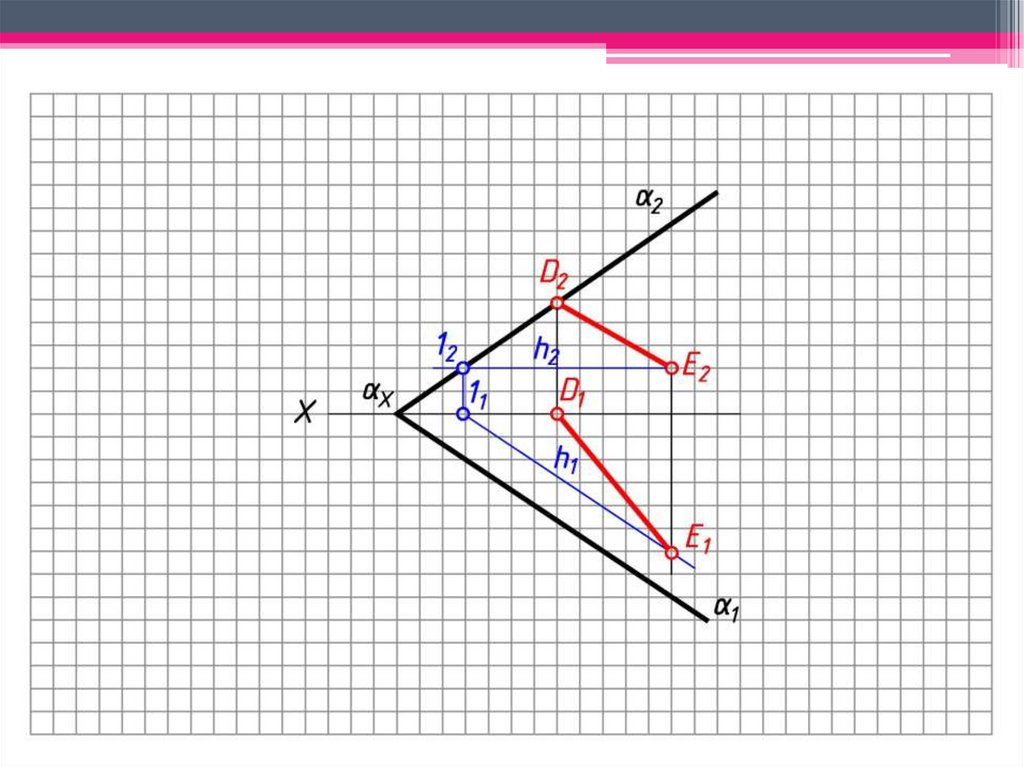
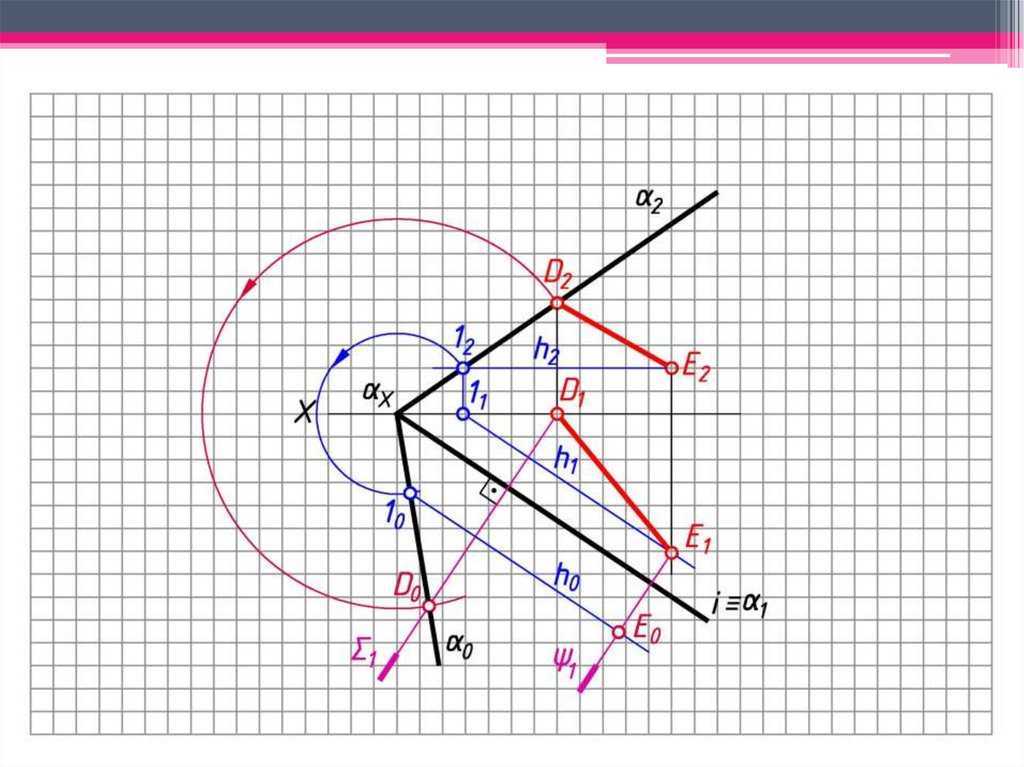
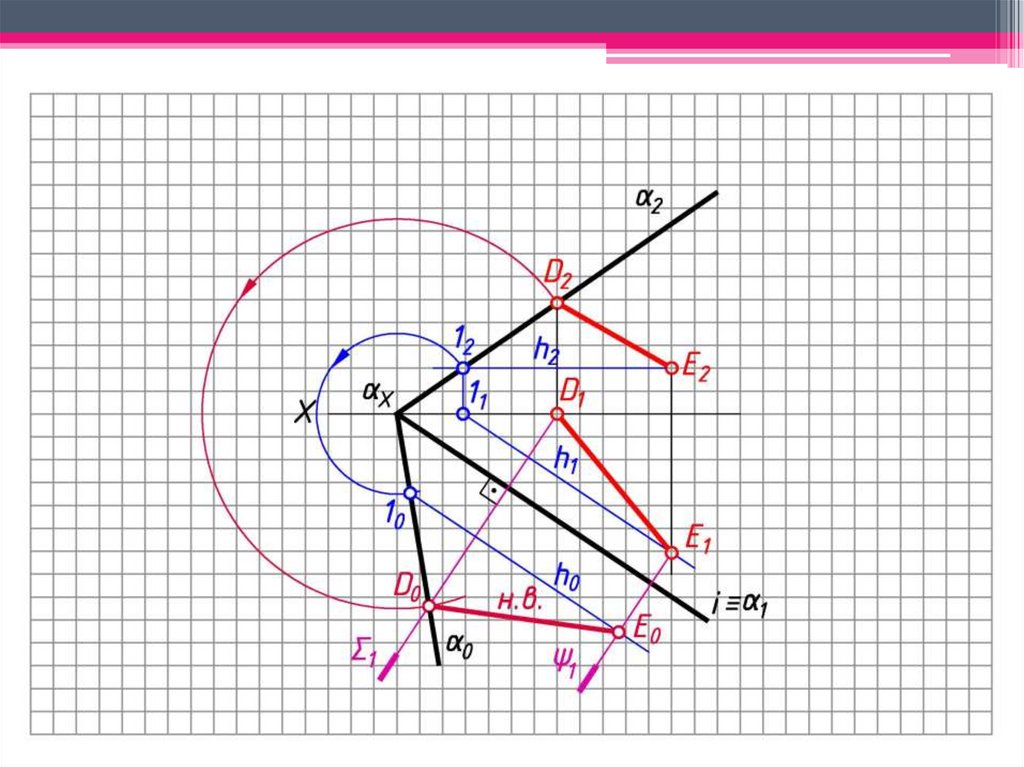
ЗАДАЧА 4: Определить н.в. отрезка (DE )
способом совмещения.
Алгоритм решения:
1. Т.к. D2 2, то D1 Х.
2. Е2 h2 E1 h1, где h1 1.
3. 1 – ось вращения.
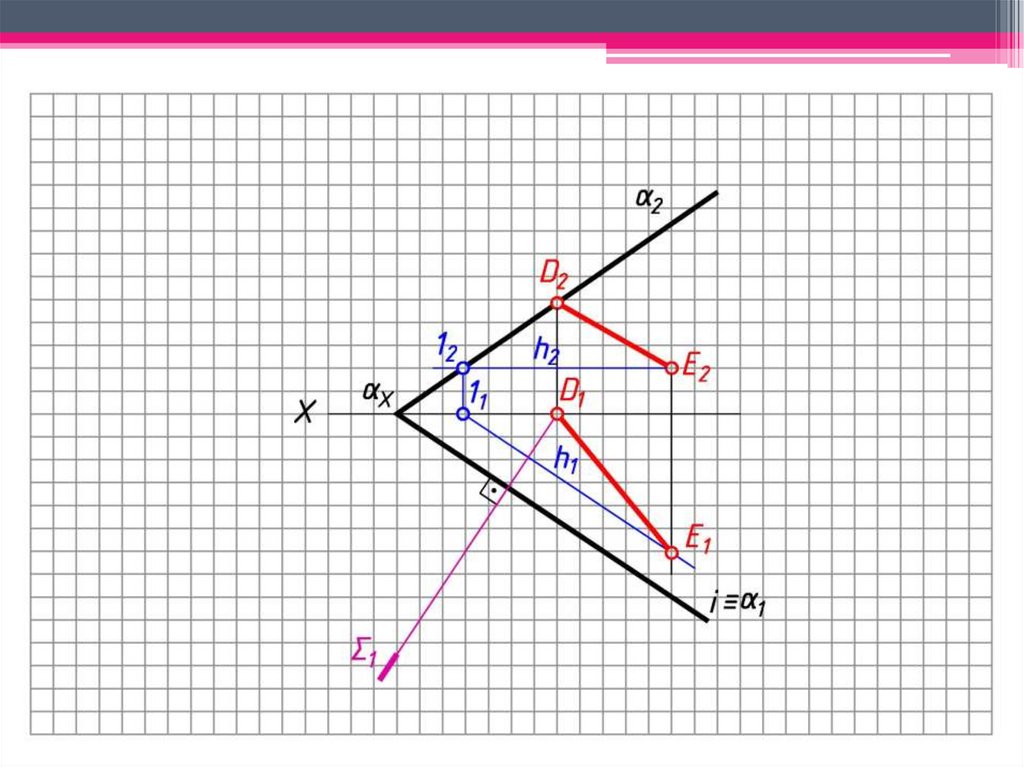
4. D2 2 D0 0.
5. 1 1 – плоскость вращения т. D, ХD2 – радиус
вращения.
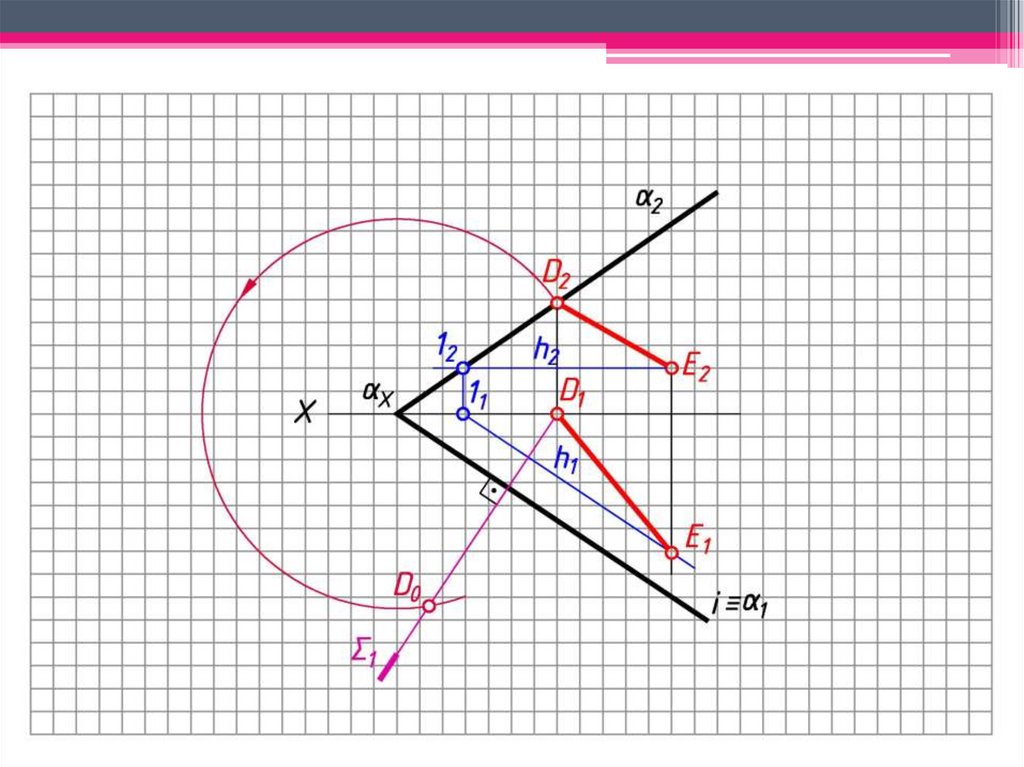
6. Окр. (ц. Х; R = ХD2) ∩ 1 = D0; 0 – совмещенный
след плоскости.
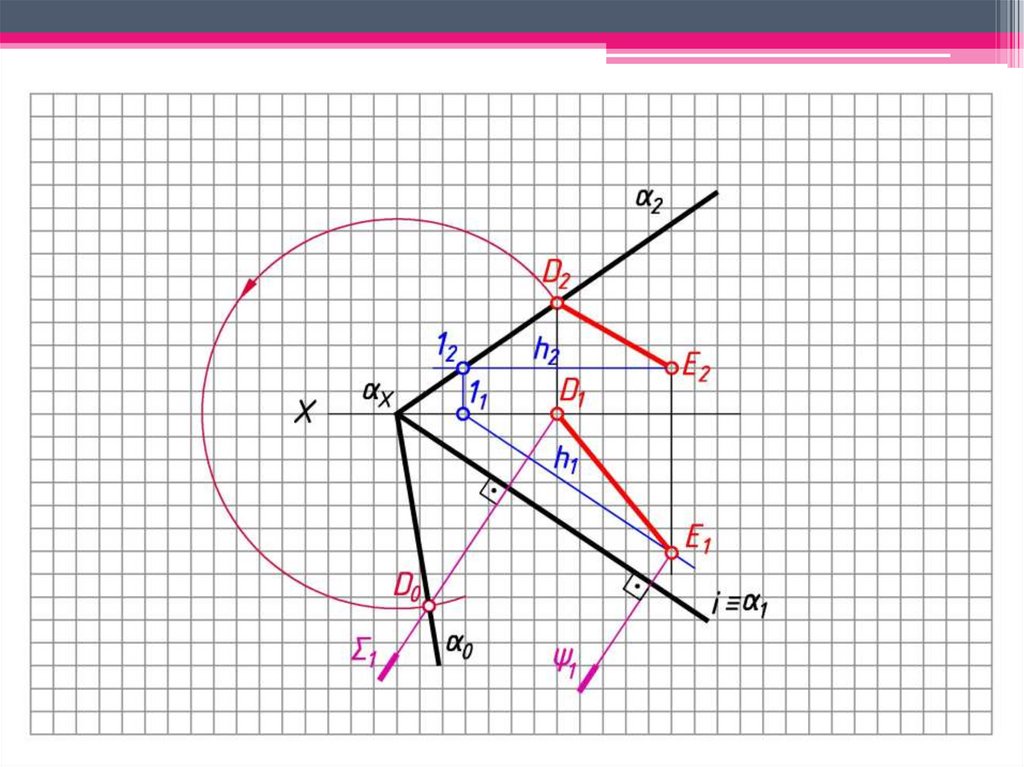
7. Т.к. Е2 h2, то E0 h0; 12 2 10 0; h0 0;
Окр. (ц. Х; R = Х12) ∩ 0 = 10;
8. 1 1 – плоскость вращения т. E.
9. h0 ∩ 1 = Е0.
10. D0E0 – н.в. DE.

27.

28.

29.

30.

31.

32.

33.

34.

35.

36.

37. Плоскопараллельное перемещение

Это вращение фигуры вокруг не выявленных
осей с последовательным ее перемещением.
Способ основан на том, что при //-ом переносе
фигуры относительно пл-ти проекций проекция
ее на эту пл-ть не меняет своей формы и
размеров, хотя и меняет положение.
В случае произвольного перемещения точки в
пл-ти, //-ой 1 ( 2) ее фронт. (гор.) проекция
перемещается по прямой, //-ой оси Х.

38.

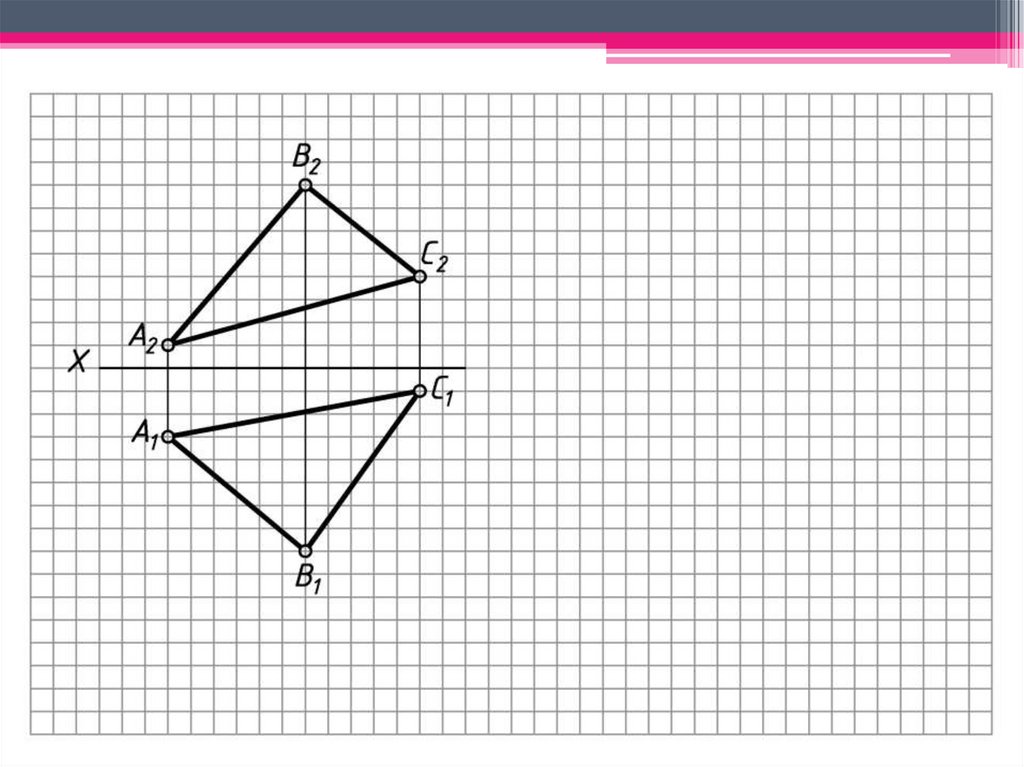
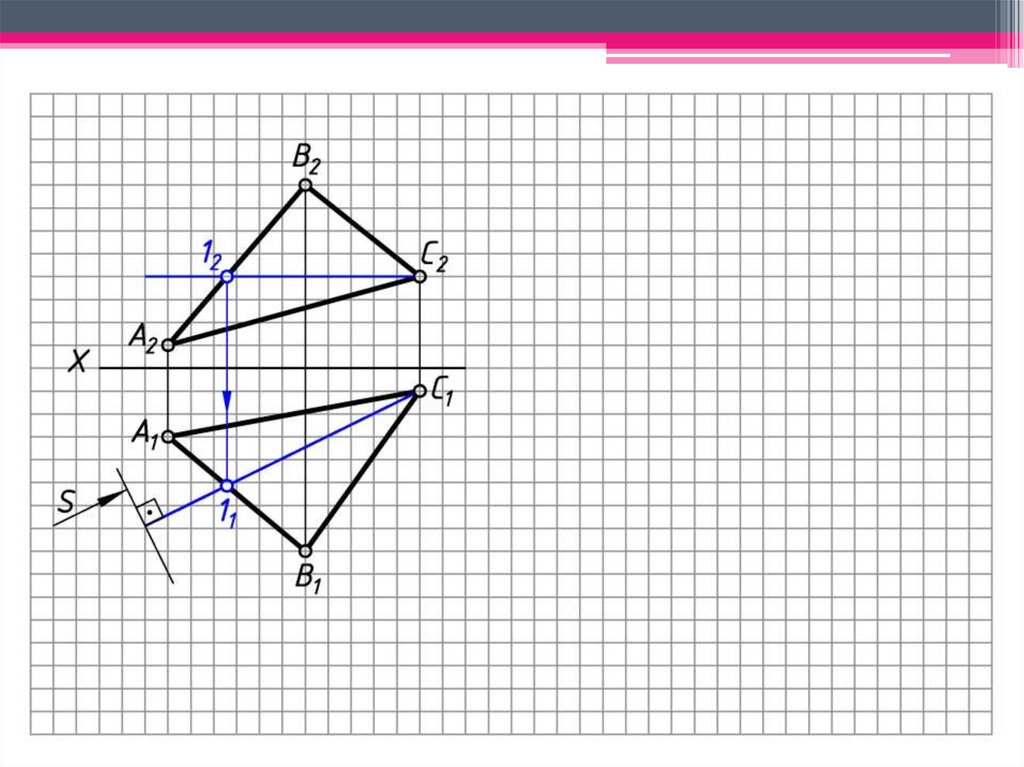
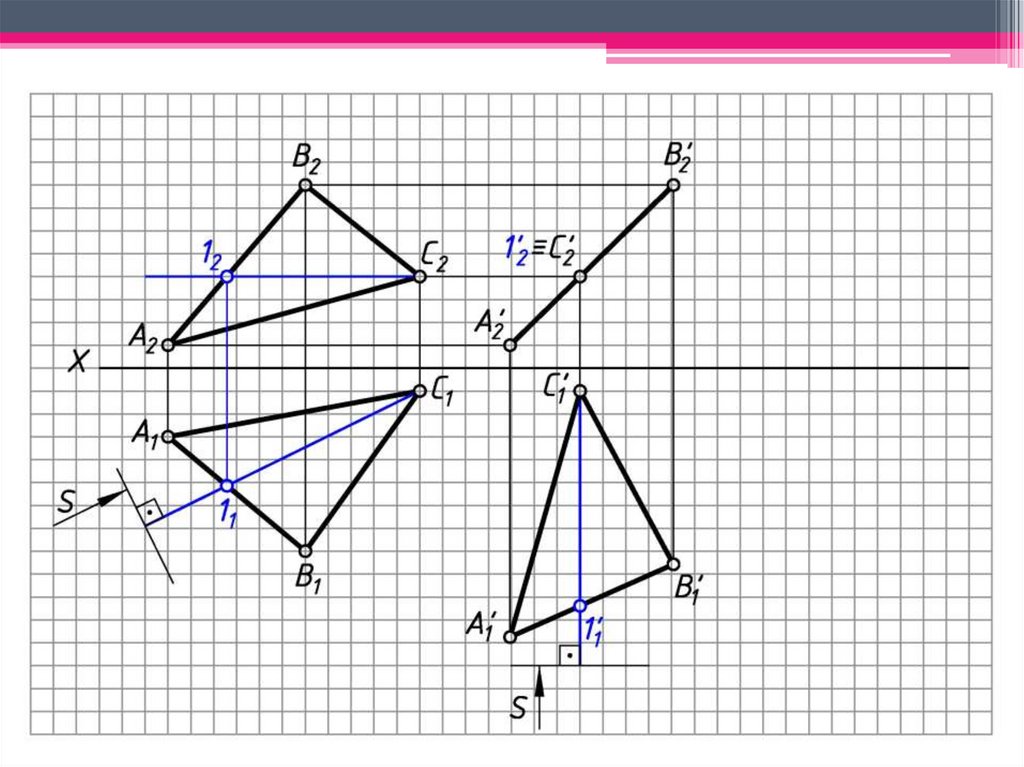
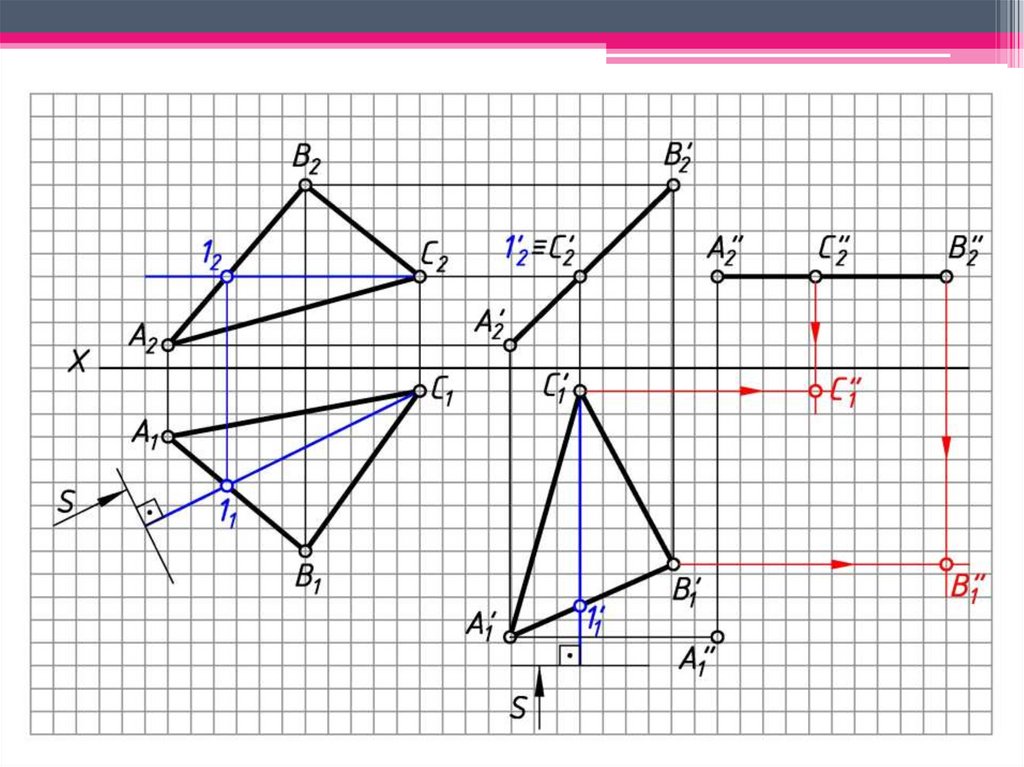
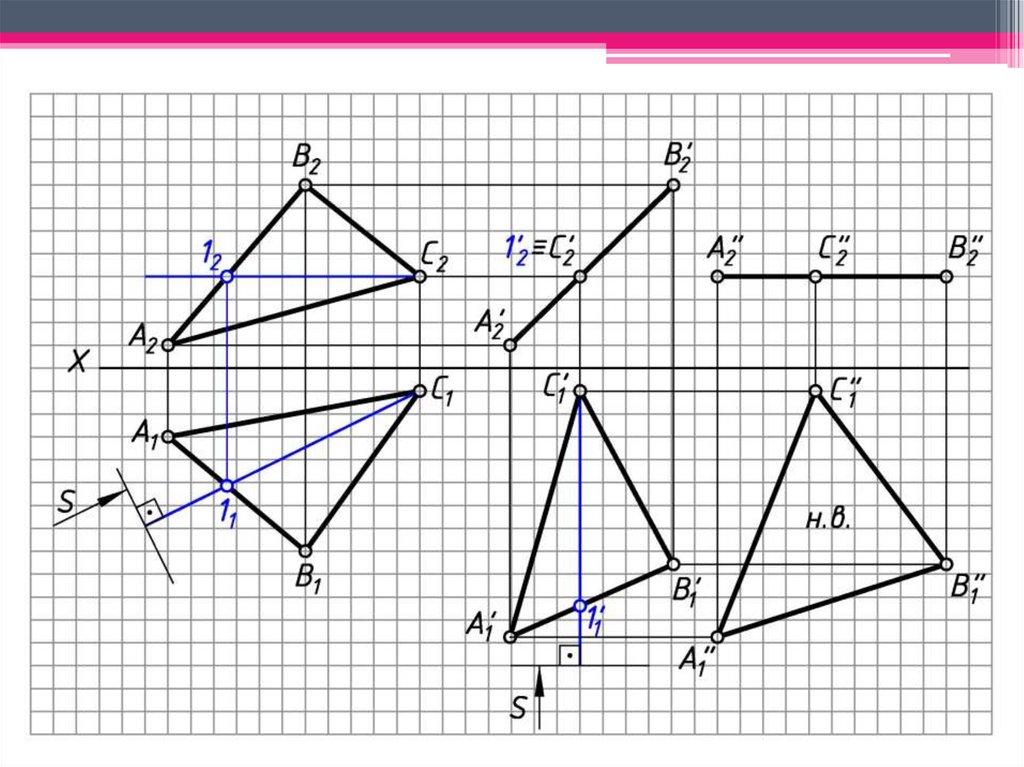
ЗАДАЧА 1: Определить н.в. АВС способом
плоскопараллельного перемещения.
Алгоритм решения:
1. Построим горизонталь В1 (В111; В212) , ктр.
определит новое направление проец-я.
2. Вращаем гор. проекцию А1В1С1 с перемещением
так, чтобы горизонталь заняла фронт.-проец.
положение (В1 2).
3. Фронт. проекции точек перемещаются по линиям,
-ым оси Х.
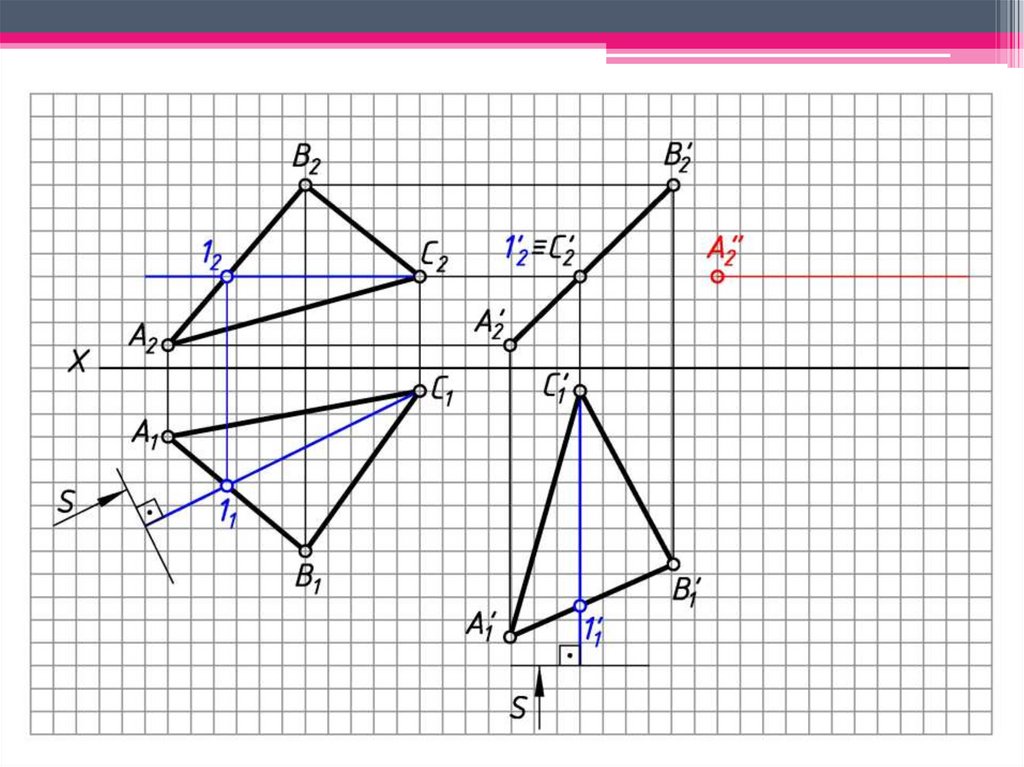
4. Пл-ть А’В’С’ займет фронт.-проец. положение (А’
В’С’ 2).
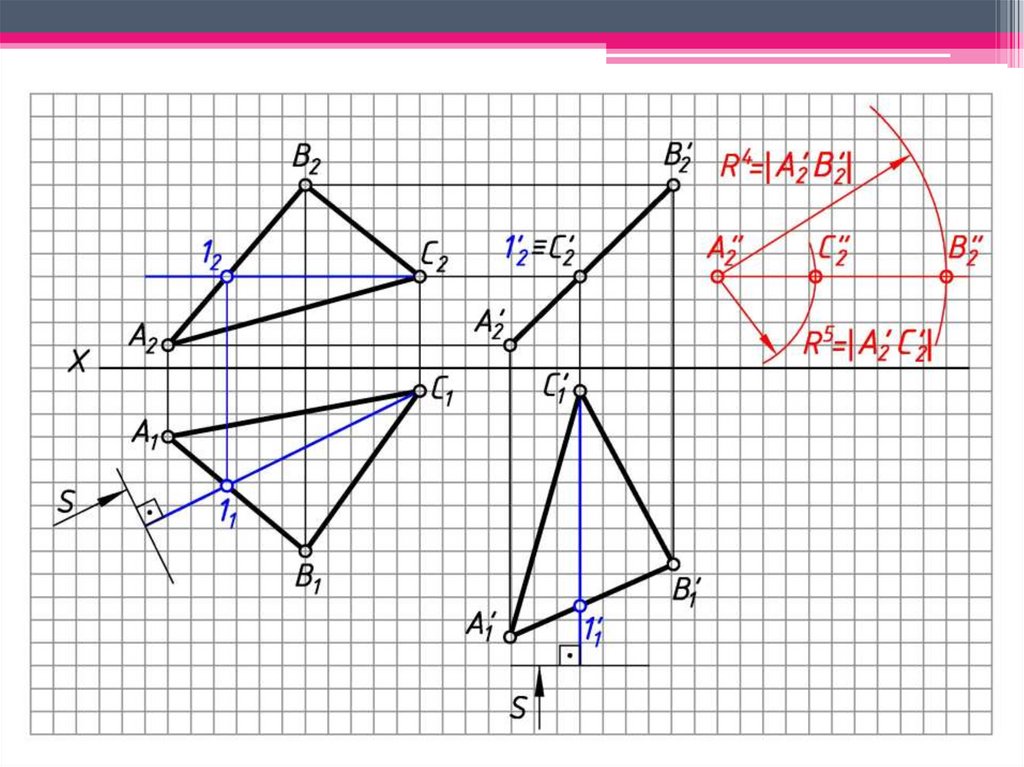
5. Вращаем фронт. проекцию А’2В’2С’2 с
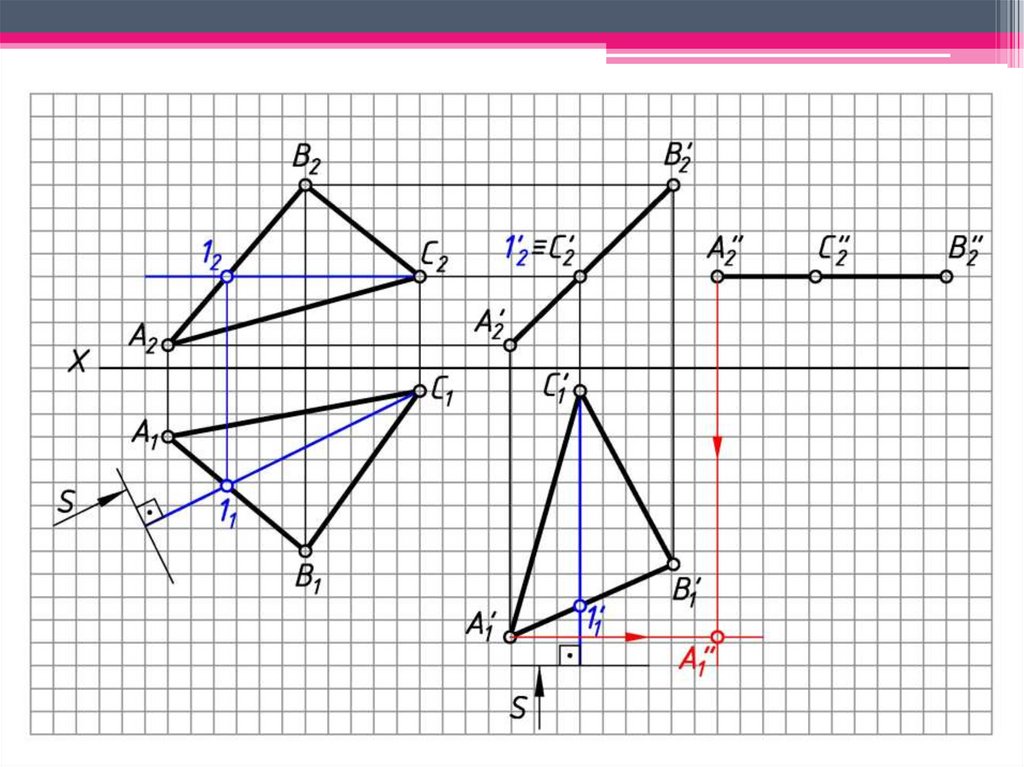
перемещением до положения гор. уровня (А” В” С”
1).
6. Гор. проекции точек перемещаются по линиям, ым оси Х.
7. А”1В”1С”1 - н.в. АВС .