Технология моделирования датчиков первичной пилотажно-навигационной информации (ДПИ) и систем на их основе

1.

Тема 3. Технология моделирования датчиков
первичной пилотажно-навигационной
информации (ДПИ) и систем на их основе

2.

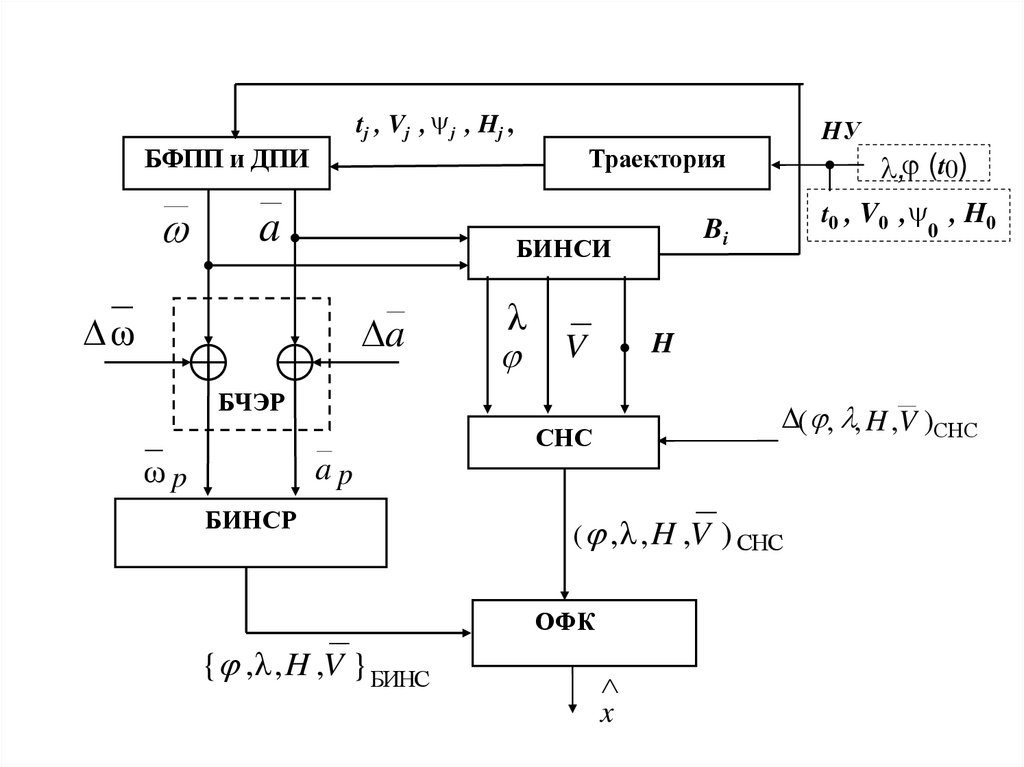
3.1. Структура математической модели
комплексной системы определения
пилотажно-навигационных параметров
полета

3.

t j , Vj , y j , H j ,
БФПП и ДПИ
l, (t0)
t0 , V0 , y , H0
Траектория
a
Bi
БИНСИ
a
ω
λ
0
H
V
БЧЭР
( , l, H ,V )СНС
СНС
ωp
HУ
ap
БИНСР
( , λ , H ,V ) СНС
ОФК
{ , λ , H ,V } БИНС
x

4.

5.

3.2. Математическая модель блока
формирования параметров полета
3.2.1. Моделирование координатных
преобразований

6. Для определения параметров движения ЛА используют базовые и подвижные системы координат (СК). За базовые принимают инерциальную

ОиXиYиZи и гринвичскую геоцентрическую ОиXYZ СК.
H
Z
НС3
N
НС1 НС2
y
x
E
z
PN
о
B
Y
ОИ
L
X

7. В инерциальной СК ось ОиXи лежит в плоскости небесного экватора (условно можно считать, что он совпадает с земным экватором) и

направлена в точку весеннего равноденствия на
небесной сфере, ось ОиZи направлена по оси вращения Земли, а ось
ОиYи составляет с осями ОиXи и ОиZи правый трехгранник.
Положение инерциальной СК относительно звезд неизменно.
В гринвичской геоцентрической СК ОиXYZ ось ОиX лежит в
плоскости земного экватора и направлена в точку пересечения
гринвичского меридиана с экватором, ось ОиZ направленна по оси
вращения Земли, а ось ОиY составляет с осями ОиX и ОиZ правый
трехгранник.
Подвижные СК на основе сопровождающих трехгранников (СТ)
применяются при инерциальном счислении пилотажнонавигационных параметров полета и представляют собой
модификации нормальной земной СК OXgYgZg. У СК OXgYgZg ось
OYg направлена вверх по местной вертикали, а оси OXg и OZg лежат
в плоскости горизонта, их направление выбирается в соответствии с
решаемой задачей.

8. Например, оси СТ оENH геодезической СК направлены следующим образом: ось оN – направлена на север параллельно касательной к

географическому меридиану в точке местонахождения ЛА;
ось оН – по геодезической вертикали;
ось оЕ – образует с осями оN и оН правый трехгранник.
Для определения углов ориентации системы координат oxyz,
связанной с блоком ДПИ, относительно инерциальной СК OXиYиZи,
а также для координатных преобразований может быть использована
универсальная матрица направляющих косинусов (МНК) B
0
b11
B 0 b21
b31
b12
b22
b32
b13
b23
b33
X
x
И
y B Y
0
И
z
Z И

9.

По элементам матрицы B могут быть найдены углы
0
ориентации связанной СК oxyz относительно инерциальной СК
ОиXиYиZи. В этом случае полагается, что начальные направления
осей указанных трехгранников совпадают, а все повороты
выполняются против часовой стрелки следующим образом:
первый – на угол y
вокруг третьей оси ОZи; второй – на
угол вокруг нового положения первой оси ОХ и ;
третий –
на угол
вокруг нового положения второй оси ОYи .
Технология координатных преобразований предполагает
также применение перестановочных матриц P
i
для переименования осей в соответствии с принятой
последовательностью вращений.
B 0 имеют вид
Элементы матрицы направляющих косинусов

10.

b11 cos y cos sin y sin sin
b12 sin y cos cos y sin sin
b13 cos sin
b21 cos sin y
b22 cos cos y
b23 sin
b31 cos y sin sin y sin cos
b32 sin y sin cos y sin cos
b33 cos cos

11.

Элементы МНК Bi и перестановочных матриц Pi
определяются путем присвоения углам y, , конкретных
значений углов, характеризующих взаимную ориентацию
трехгранников в соответствии с таблицей.
B0
B1
B2
B3
B 3*
y
t
λ
yг
ψ
0
0
0
B4
P3
A
/2
/2
0
0
0

12.

, l
– соответственно геодезические широта и долгота ЛА;
y, , – углы Эйлера, определяющие ориентацию связанной с
блоком ДПИ системы координат oxyz относительно инерциальной
ОиXиYиZи;
– углы Эйлера (тангаж, крен), определяющие ориентацию
связанной с ЛА системы координат oxyz относительно плоскости
горизонта; y г - угол гироскопического курса БДПИ
относительно осей трехгранника о ;
B1 – МНК, характеризующая взаимную ориентацию осей
инерциальной ОXиYиZи и гринвической геоцентрической ОXYZ
систем координат;
t t t 0
B2 – МНК, характеризующая взаимную ориентацию осей
гринвичской геоцентрической СК ОXYZ и сопровождающего
трехгранника оENH геодезической системы координат;

13.

оENH и опорного трехгранника о ;
B3 – МНК, характеризующая взаимную ориентацию осей
опорного трехгранника о и связанной СК oxyz. При А=0 МНК
характеризует взаимную ориентацию осей СК oxyz и СТ оENH;
– значение угловой скорости вращения Земли;
А – азимутальный угол опорного навигационного трехгранника
о относительно геодезического сопровождающего
трехгранника оENH. Опорный трехгранник применяется для
реализации всеширотного алгоритма счисления координат.

14.

Дополнение к лекции 8

15.

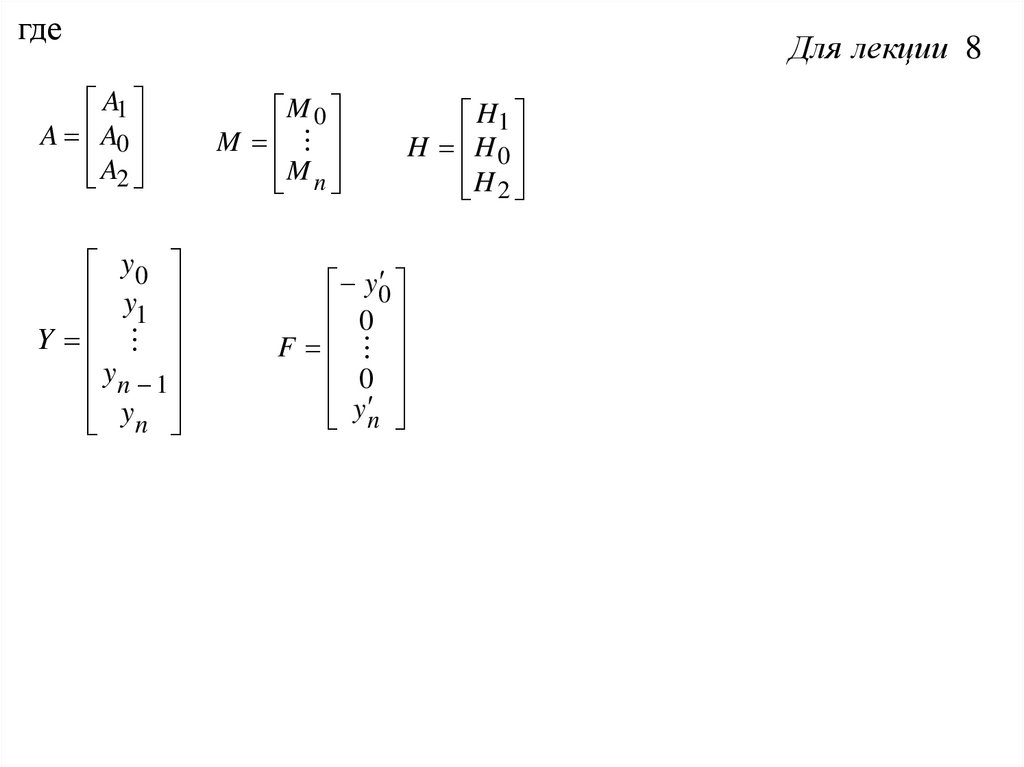
где
A1
A A0
A
2
y0
y
1
Y
yn 1
y n
Для лекции 8
M 0
M
M
n
y0
0
F
0
y
n
H1
H H 0
H
2

16.

Для лекции 8
2
1 1 2
0
0
0
0
0
0
0
6
3
6
2 3 3
2
0 0
0
0
0
0
0
6
3
6
A0
n 2 n 2 n 1
n 1
0
0
0
0 0 0
0
6
3
6
n 1
n 1 n n
0
0
0 0 0
0
0
6
3
6

17.

1 2
1
1
0
1 2
2
1
3 1
1
0
2
2
2 3
3
H 0
0
0
0
0
0
0
0
0
1
A1
3
1
1
H1
1
6
1
0
0
1
n 2
0
0
0 0
0
0
0
n 2 n 1
1
n 2 n 1
n 1
1
n 1
n
A2 0 0
6
0 0
1
n
n 1
n 1 n
n
1
H 2 0 0
n
Для лекции 8
3
1
n
0
0
..
0
1
n

18.

Структурная схема рекуррентной процедуры сплайн-сглаживания
Коэффициенты сплайна и его производных
Для лекции 8
Сплайн и его производные
да
t := t+ hag
t < ti+1
нет
i :=i+1