Similar presentations:
Авиагоризонты и гировертикали. Применение 3-х степенного гироскопа для измерения углов крена и тангажа
1. Лекция № 6
Раздел 1. Гироскопические приборы и системыТема 1.2 Авиагоризонты и гировертикали
Применение 3-х степенного гироскопа для
измерения углов крена и тангажа
1. Причины «ухода» свободного 3-х степенного
гироскопа с вертикально расположенным вектором
кинетического момента
2. Уравнения «ухода» свободного 3-х степенного
гироскопа с вертикально расположенным вектором
кинетического момента
2. 1. Причины «ухода» свободного 3-х степенного гироскопа с вертикально расположенным вектором кинетического момента
22Принцип действия гироскопических авиагоризонтов основан на
использовании свойства трехстепенного гироскопа сохранять заданное
направление кинетического момента неизменным в пространстве. Углы
крена и тангажа ϑ самолета измеряют с помощью трехстепенного
гироскопа (рис. ), установленного на самолете.
z
ДУ
y
ДУ
x
Рисунок 1.5
Направление кинетического
момента гироскопа
совпадает с вертикалью
места (ось ОZ), внешняя ось
карданова подвеса
совпадает с продольной
осью самолета OX, а
внутренняя — направлена по
оси ОY, расположенной в
горизонтальной плоскости.
3. 1. Причины «ухода» свободного 3-х степенного гироскопа с вертикально расположенным вектором кинетического момента
zДУ
y
ДУ
x
Рисунок 1.5
21
При появлении угла тангажа
внешняя ось подвеса поворачивается
вместе с самолетом, а гироузел не
изменяет своего положения в
пространстве. Вследствие этого угол
поворота наружной рамы относительно
внутренней оси карданова подвеса равен
углу тангажа ϑ.
При накренении самолета вместе
с ним поворачивается основание, на
котором закреплен гироскоп. Наружная
рама остается неподвижной. Угол
поворота основания относительно
наружной рамы равен углу крена
самолета .
4. 1. Причины «ухода» свободного 3-х степенного гироскопа с вертикально расположенным вектором кинетического момента
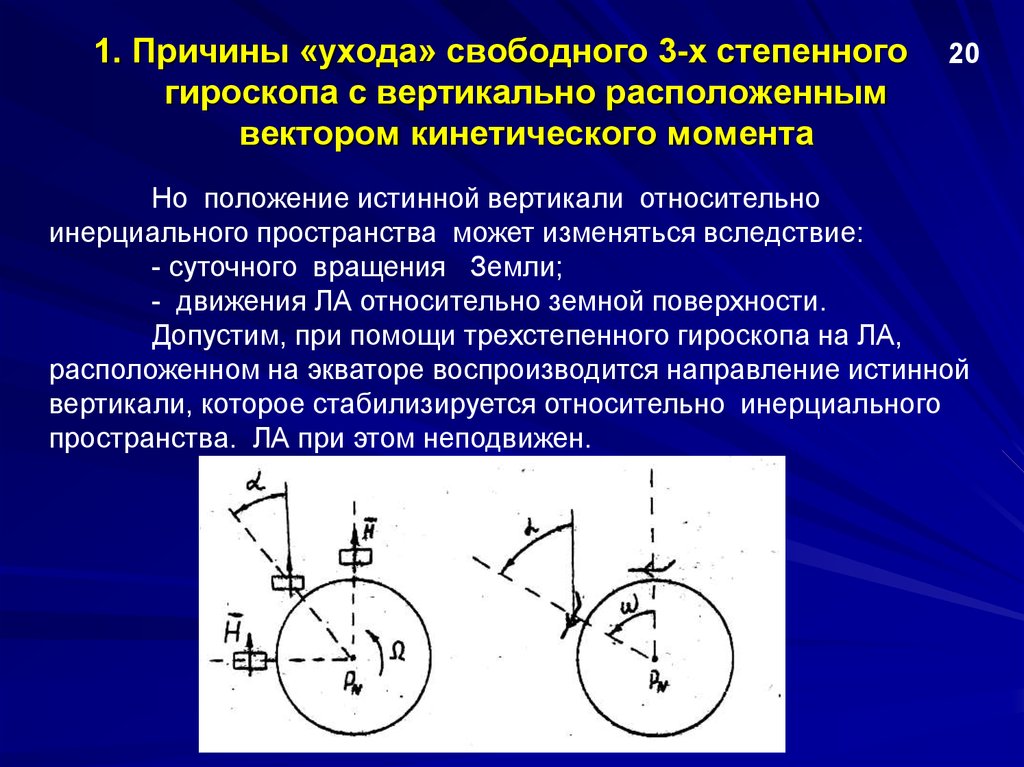
20Но положение истинной вертикали относительно
инерциального пространства может изменяться вследствие:
- суточного вращения Земли;
- движения ЛА относительно земной поверхности.
Допустим, при помощи трехстепенного гироскопа на ЛА,
расположенном на экваторе воспроизводится направление истинной
вертикали, которое стабилизируется относительно инерциального
пространства. ЛА при этом неподвижен.
5. 1. Причины «ухода» свободного 3-х степенного гироскопа
19Если не принимать никаких дополнительных мер, то даже при
неподвижном ЛА с течением некоторого времени наблюдатель заметит,
что вектор Н гироскопа отклонился от заданного направления. На
самом деле отклонилась поверхность Земли вследствие суточного
вращения и теперь истинная вертикаль занимает новое положение в
инерциальном пространстве, составляя некоторый угол с
моделируемой при помощи ГС вертикалью (рис., а). Очевидно, что
через 6 часов гироскоп из вертикального станет горизонтальным. Это
явление получило название "кажущегося ухода" гироскопа из-за
вращения Земли.
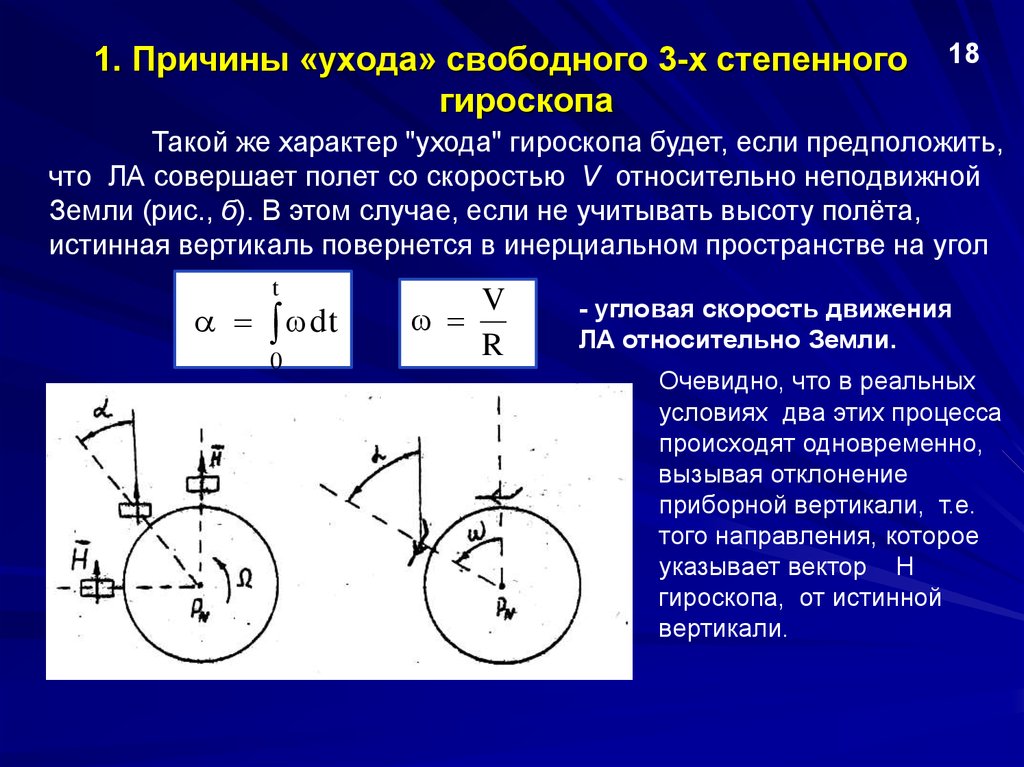
6. 1. Причины «ухода» свободного 3-х степенного гироскопа
18Такой же характер "ухода" гироскопа будет, если предположить,
что ЛА совершает полет со скоростью V относительно неподвижной
Земли (рис., б). В этом случае, если не учитывать высоту полёта,
истинная вертикаль повернется в инерциальном пространстве на угол
t
dt
0
V
R
- угловая скорость движения
ЛА относительно Земли.
Очевидно, что в реальных
условиях два этих процесса
происходят одновременно,
вызывая отклонение
приборной вертикали, т.е.
того направления, которое
указывает вектор Н
гироскопа, от истинной
вертикали.
7. 1. Причины «ухода» свободного 3-х степенного гироскопа
17Таким образом, в общем случае вектор Н гироскопа будет
уходить от требуемого
направления стабилизации с угловой
скоростью , равной сумме угловых скоростей кажущегося ухода
из-за вращения Земли (переносное движение), из-за облёта Земли
ЛА с угловой скоростью ω (относительное движение), а также из-за
инструментальных дрейфов гироскопов
:
др
др
(6.1)
8. 2. Уравнения «ухода» свободного 3-х степенного гироскопа с вертикально расположенным вектором кинетического момента
16Особенностью трехстепенного гироскопа является то, что
направление его кинетического момента сохраняется неизменным в
мировом пространстве, а не относительно Земли. В связи с этим из-за
собственного вращения Земли и перемещения самолета относительно
Земли вертикаль места будет отклоняться от направления
кинетического момента гироскопа.
Рассмотрим это явление, пренебрегая при этом высотой полета
по сравнению с радиусом Земли.
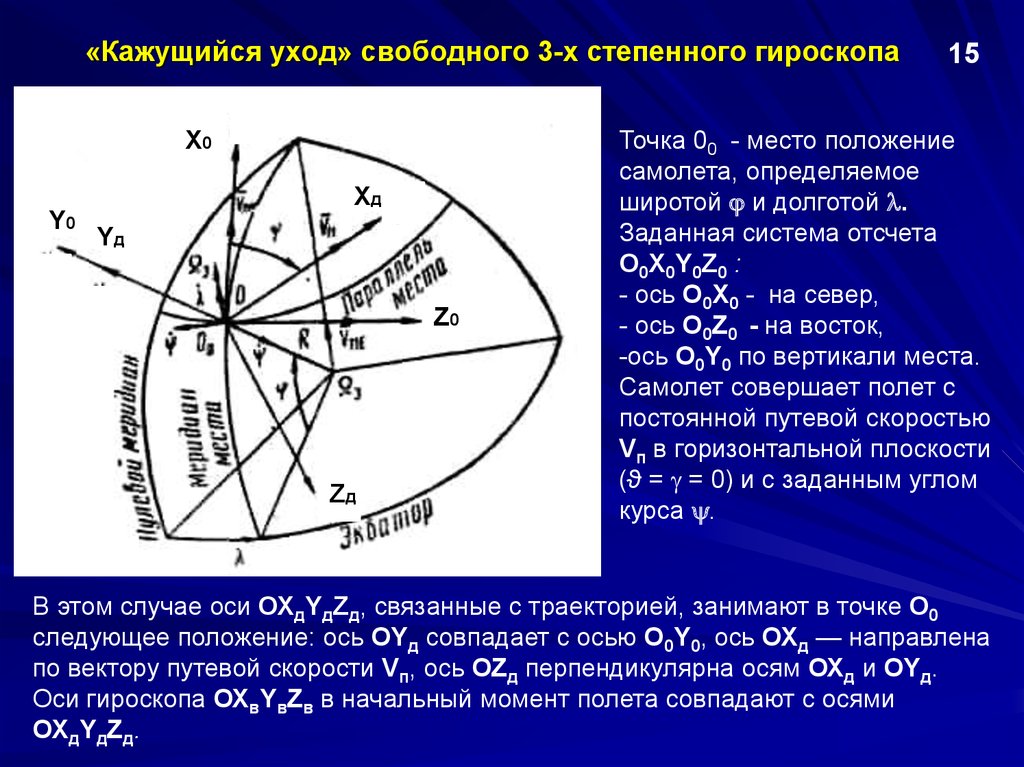
9. «Кажущийся уход» свободного 3-х степенного гироскопа
X0Xд
Y0
Yд
Z0
Zд
15
Точка 00 - место положение
самолета, определяемое
широтой и долготой .
Заданная система отсчета
О0Х0Y0Z0 :
- ось О0Х0 - на север,
- ось О0Z0 - на восток,
-ось О0Y0 по вертикали места.
Самолет совершает полет с
постоянной путевой скоростью
Vп в горизонтальной плоскости
(ϑ = = 0) и с заданным углом
курса .
В этом случае оси ОХдYдZд, связанные с траекторией, занимают в точке О0
следующее положение: ось ОYд совпадает с осью О0Y0, ось ОХд — направлена
по вектору путевой скорости Vп, ось ОZд перпендикулярна осям ОХд и ОYд.
Оси гироскопа ОХвYвZв в начальный момент полета совпадают с осями
ОХдYдZд.
10. «Кажущийся уход» свободного 3-х степенного гироскопа
14Составляющие путевой
скорости:
VпN = Vп cos ,
(6.2)
VпE = Vп sin .
VпN – северная
VпE – восточная
VпN
V сos
п
,
R
R
(6.3)
V
V
sin
пЕ
п
R cos R cos
R - радиус Земли
11. «Кажущийся уход» свободного 3-х степенного гироскопа
13Проекции угловой скорости
вращения трехгранника ОХдYдZд в
пространстве на эти оси
Х Д sin ( з ) cos cos ,
YД ( з ) sin ,
(6.4)
ZД cos ( з ) cos sin .
- угловая скорость вращения Земли
С учетом выражений
(6.2), (6.3)
Х Д з cos cos ,
YД
Z Д
Vп sin
з sin
tg ,
R
V
з cos sin п .
R
(6.5)
12. «Кажущийся уход» свободного 3-х степенного гироскопа
12Угловые скорости Х Д , YД , Z Д
характеризуют скорость
рассогласования осей трехгранника
ОХдYдZд, перемещающегося вместе с
самолетом и сохраняющего ось ОYд
вертикальной, и неподвижного в
мировом пространстве трехгранника
ОХвYвZв.
,
ХД
ZД
Угловые скорости
определяют скорость «ухода» кинетического момента гироскопа от вертикали места вследствие суточного вращения
и движения самолета относительно Земли. За час полета углы отклонения
кинетического момента от вертикали могут достигать нескольких градусов.
Кроме того, гироскоп отклоняется от заданного положения из-за
наличия моментов трения в осях подвеса и моментов от небаланса.
13. «Кажущийся уход» свободного 3-х степенного гироскопа
11В связи с этим трехстепенной
гироскоп может быть использован
как невозмущаемый указатель
вертикали места лишь в течение
нескольких минут. Для обеспечения
более длительной работы
трехстепенного гироскопа как
указателя вертикали с необходимой
точностью его следует снабдить
корректирующим устройством.
В качестве чувствительных элементов корректирующих
устройств в авиагоризонтах используют однокоординатные и двух
координатные электролитические маятники.
14. «Кажущийся уход» свободного 3-х степенного гироскопа
YдYв
Хд
Zв
На гироузле 2 располагается двухкоординатный
электролитический маятник 5, управляющий двумя коррекционными
двигателями 1, 6. На внешней и внутренней осях карданова подвеса
располагаются устройства для съема результатов измерений 3, 4.
10
15. Уравнения «ухода» свободного 3-х степенного гироскопа
9Для получения уравнений движения гироскопа воспользуемся
методом суммирования моментов. Суммируя моменты, действующие
по внешней и внутренней осям карданова подвеса, получаем
M и х M г х M т х M к х 0,
н
н
н
Mи zв Mг zв M т zв
Ми - моменты инерции;
н
Мг - гироскопические моменты;
(6.6)
Мт - моменты трения;
M к z в 0.
Мк- корректирующие моменты.
;
г , M и z В
M и х н А
г
в
M т х н f г M т sgn г ;
Моменты инерции и моменты
(6.7) трения
M т z в f г M т sgn г ,
M г х н M г х в cos г Н аZ В cos г ,
Mг zв
Н аХ В .
(6.8)
Гироскопические моменты
аZ В , аХ В
проекции абсолютной
угловой скорости
движения гироскопа в
мировом пространстве
16. Уравнения «ухода» свободного 3-х степенного гироскопа
8Проектируем угловые скорости на оси ОХв и ОZв
аХ В г cos г Z Д sin г sin г Х Д cos г YД cos г sin г ;
аZ В г Z Д cos г sin г YД sin г .
(6.9)
Полагая углы г и г малыми, из (6.8), с учетом (6.9) получаем
M г х н Н( г Z Y г ),
Д
Д
M г z в Н( г Х Y г ).
Д
(6.10)
Д
Выражения для корректирующих моментов
M к х н с1 м , M к z в с 2 м .
(6.11)
с1, с2 - коэффициенты пропорциональности системы коррекции;
м, м - углы отклонения осей корректирующих маятников по отношению к осям
гироузла
17. Уравнения «ухода» свободного 3-х степенного гироскопа
7Значения углов отклонения осей корректирующих маятников
м = - г+ мв,
м= - г+ мв,
(6.12)
мв, мв — отклонения маятников, обусловленные действием
внешних возмущений (ускорения при маневрировании и
вибрации).
Знаки корректирующих моментов в выражениях (6.10) выбраны таким
образом, чтобы при отклонении гироскопа от вертикали он
возвращался бы к ней под влиянием корректирующих моментов.
Уравнения движения авиагоризонта (6.6) с учетом выражений
(6.7), (6.10-6.12) запишутся в виде
г Н( г Z Y г ) f г M т sgn г с1 г с1 мв ,
А
Д
Д
Н( ) f M sgn с с .
В
г
г
г
т
г
2 г
2 мв
Х
Y г
Д
(6.13)
Д
Методические погрешности складываются из скоростных и баллистических
девиаций авиагоризонта.
18. «Кажущийся уход» свободного 3-х степенного гироскопа, обусловленный движением самолета
6Для определения скоростных девиаций рассмотрим уравнения
(6.13) для случая прямолинейного движения самолета с
постоянной скоростью ( YД = мв = мв =
=0) и без учета
инерционности рам карданова подвеса и трения в осях подвеса.
Н( г Z ) с1 г ,
г k1 г Z ,
Н( г Х ) с 2 г
г k 2 г Х
Д
Д
Д
k1 = c1/H, k2 = c2/H.
Частные решения уравнений (6.14)
0г
Z
Д
k1
(6.14)
Д
,
0г
X
Д
k2
19. «Кажущийся уход» свободного 3-х степенного гироскопа, обусловленный движением самолета
Частные решения уравнений (6.14)являются скоростными девиациями
авиагоризонта. У современных
авиагоризонтов значения скоростных
девиаций составляют несколько
угловых секунд.
0г
Z
Д
k1
,
0г
X
5
Д
k2
Из изложенного следует, что при введении пропорциональной коррекции трехстепенной гироскоп не «уходит» от вертикали места
под действием угловых скоростей
Z и Х
Д
Д ,
а устанавливается в положение, практически не отличающееся от
вертикального.
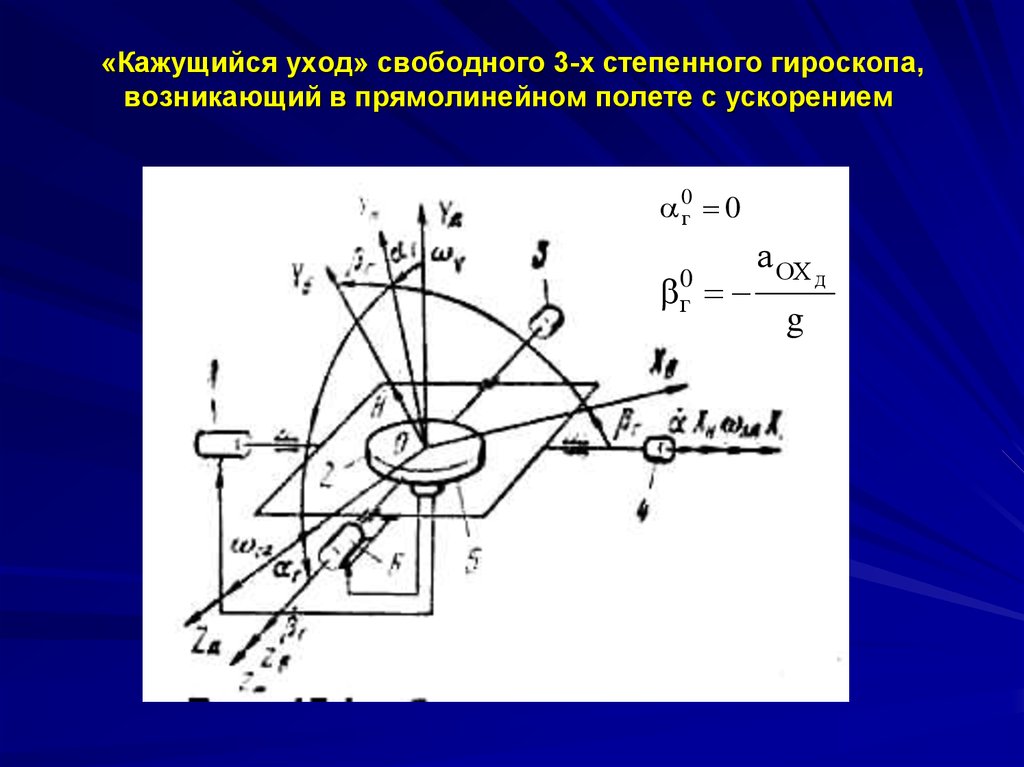
20. «Кажущийся уход» свободного 3-х степенного гироскопа, возникающий в прямолинейном полете с ускорением
4Баллистические девиации представляют собой погрешности
авиагоризонта при маневрировании самолета.
Рассмотрим случай прямолинейного движения самолета
= 0 с постоянным ускорением а .
ОХ Д
Пренебрегая малыми угловыми скоростями Z Д и Х Д ,
и без учета инерционности рам карданова подвеса и трения в
осях подвеса систему уравнений (6.13)
г Н( г Z Y г ) f г M т sgn г с1 г с1 мв ,
А
Д
Д
Н( ) f M sgn с с .
В
г
г
г
т
г
2 г
2 мв
Х
Y г
Д
запишем в виде
(6.13)
Д
г k1 г k1
а ОХ
g
Д
, г k 2 г 0.
k1 = c1/H, k2 = c2/H.
(6.15)
21. «Кажущийся уход» свободного 3-х степенного гироскопа, возникающий в прямолинейном полете с ускорением
0Решением второго уравнения (6.15) является равенство
г 0 .
Первое уравнение при нулевых начальных условиях имеет
следующее решение:
г
а ОХ
Д
g
(1 e k 1 t )
(6.16)
Таким образом, как следует из уравнения (6.16), ось гироскопа
авиагоризонта при действии продольного ускорения
апериодически приближается к положению кажущейся вертикали,
при этом
0г
а ОХ
g
Д
3
22. «Кажущийся уход» свободного 3-х степенного гироскопа, возникающий в прямолинейном полете с ускорением
0г 00г
а ОХ
g
Д
23. «Кажущийся уход» свободного 3-х степенного гироскопа, обусловленный «дрейфом»
2Основные причины возникновения дрейфа гироскопа:
- разбалансировка (дебаланс), т.е. несовпадение центра подвеса
гироузла с центром масс гироскопа;
- моменты сил сухого и жидкостного (вязкого) трения;
- моменты токоподводов;
- моменты датчиков углов;
- моменты сил инерции рам карданова подвеса и др.
Рассмотрим инструментальные погрешности, обусловленные
наличием сухого трения в осях подвеса. Пренебрегая
инерционностью рам карданова подвеса, вязким трением в подвесе,
малыми угловыми скоростями
Z и Х
Д
Д
=0; мв = мв = 0, и без учета инерционности рам
и полагая
карданова подвеса уравнения (6.13) запишем в виде:
M sgn г
Mт
k т
,
г
1 г
H
H
(6.17)
M т sgn г
Mт
г k 2 г
.
H
H
24. «Кажущийся уход» свободного 3-х степенного гироскопа, обусловленный «дрейфом»
г k1 гM т sgn г
г k 2 г
H
M т sgn г
H
Mт
H
Mт
H
,
(6.17)
.
Решениями уравнений (6.17) являются:
г 0г (1 e k 1 t ) н e k 1 t ,
г 0г (1 e k 2 t ) н e k 2 t ,
0г
Mт
k1H
,
0г
Mт
k 2H
,
н = г(0), н = г(0).
Из решений (6.17) следует, что при отклонении авиагоризонта на
углы н и н ось его гироскопа не может возвратиться в
вертикальное положение, а будет составлять с вертикалью места
углы 0 и 0 , определяющие зону застоя от трения.
г
г
1
25. «Кажущийся уход» свободного 3-х степенного гироскопа, обусловленный «дрейфом»
0г0г
Mт
Mт
k1H
k 2H
,
,





















 geography
geography








