Разбор олимпиадных задач

1. Разбор олимпиадных задач.

2. В системе, изображенной на рисунке, прикрепленные к невесомым пружинам грузики при помощи нитей удерживаются на расстоянии l\2

Задача 1.
В системе, изображенной на рисунке, прикрепленные к
невесомым пружинам грузики при помощи нитей
удерживаются на расстоянии l\2 от стенок, к которым
прикреплены концы пружин. Длины обеих пружин в
недеформированном состоянии одинаковы и равны L.
Нити одновременно пережигают, после чего грузики
сталкиваются и слипаются. Найдите максимальную
скорость, которую будут иметь грузики при колебаниях,
возникших после этого столкновения. Удар при
столкновении является центральным и абсолютно
неупругим.
Трением и размерами грузиков пренебречь.

3.

Решение
Направим координатную ось вправо и поместим начало
координат посередине между стенками. Тогда после
пережигания нитей левый грузик будет двигаться по закону
X1(t)=-L\2cos(t√(2k\m)), здесь L\2 - амплитуда, √(2k\m) частота (1)
Здесь учли, что период колебаний пружинного маятника
T=2π √(k\m), ω=2π\T, ω= √(k\m) (2)
Для второго грузика аналогично запишем
X2(t)=L\2cos(t√(k\2m))(3)
Грузики столкнутся через время t0, которое определяется из
условия X1(t)=X2(t).

4.

-L\2cos(t0√(2k\m))=L\2cos(t0√(k\2m))
(4)
По формуле суммы косинусов получим из (4)
2cos(1\2(√(2k\m)+√(k\2m))t0)*2cos(1\2(√(2k\m)√(k\2m))t0)=0 (5)
Из (5) следует, что
cos(1\2(√(2k\m)+√(k\2m))t0)=0 или
cos(1\2(√(2k\m)-√(k\2m))t0)=0 (6)
Из всех решений выберем наименьшее
положительное, которое получается из условия
1\2(√(2k\m)+√(k\2m))t0=π\2
(7)

5.

Из (7) следует t0=π\3√(2k\m)
(8)
В момент столкновения грузики будут иметь координату
X0= L\2cos(t0√(k\2m)= L\2cos(π\3√(2k\m) √(k\2m))=L\4 (9)
Скорости левого и правого грузиков перед столкновением
будут равны
U1= L\2 √(2k\m)sin(t0√(2k\m))= L\2√(2k\m)(√3\2)
(10)
U2=-L\2 √(k\2m)sin(t0√(k\2m))=-L\2√(k\2m)(√3\2) (11)
Скорость грузиков непосредственно после соударения
найдем из закона сохранения импульса (учтем (10) и (11))
U=(mu1+2mu2)\(m+2m)
(12)
Скорость грузиков после удара равна нулю, а удлинения
пружин отличны от нуля и равны
X0=L\4

6.

Следовательно, после столкновения слипшиеся грузики
будут совершать колебания с амплитудой X0 и частотой
ω=√((k+2k)\(m+2m))=√(k\m)
(14)
В процессе этих колебаний максимальная скорость грузиков
будет равна
Umax=ωX0=L\4√(k\m)
Ответ: Umax=ωX0=L\4√(k\m)
(15)

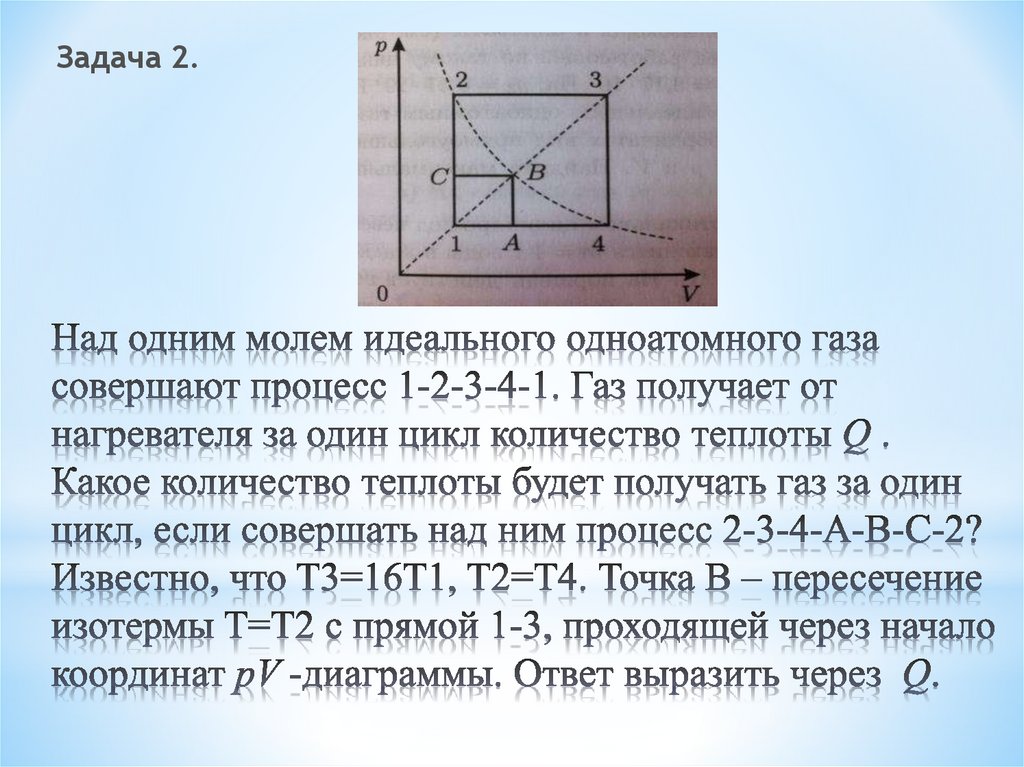
7. Над одним молем идеального одноатомного газа совершают процесс 1-2-3-4-1. Газ получает от нагревателя за один цикл количество

Задача 2.

8.

Решение
Рассмотрим сначала исходный цикл и выразим количество
теплоты через другие параметры системы.
Q=∆U+A (1)
Теплота сообщается газу на участках 1-2 и 2-3, следовательно,
количество теплоты, сообщенное газу за один цикл
Q=Q1+Q2=3\2vR(T2-T1)+5\2vR(T3-T2)
(2)
Выразим T2 через T1. Для этого рассмотрим участки 1-2 и 3-4.
Запишем для них p1\T1=p2\T2, p3\T3=P4\T4 (3)
Здесь p2=p3, p1=p4, T2=T4
(4)
Тогда из (3) и (4) получаем p2\T3=p1\T2
(5)
Из (3) и (5) получим p1\p2=T1\T2=T2\T3, сл-но T2=√(T1*T3)
(6)
По условию Т3=16Т1, значит Т2=4Т1.
(7)

9.

Из (2) с учетом (7) получим
Q=3\2vR(4T1-T1)+5\2vR(16T1-4T1)=69\2vRT1
(8)
Теперь рассмотрим цикл 2-3-4-А-В-С-2. Теплота Q1 сообщается газу
на участках С-2, 2-3, А-В. Очевидно, что Q1=Q-QAC+QAB (9)
QAC=3\2vR(Tc-T1), QAB=3\2vR(TB-TA)
(10)
Выразим TA, TB, TC через Т1. По аналогии с циклом 1-2-3-4, с
учетом того, что ТВ=Т2=4Т1, можно для цикла 1-С-В-А-1
записать
ТА=√(Т1ТВ)=√(Т1Т2)=2Т1=Тс
(11)
Подставим (11) в (10)
Q1=69\2vRT1-3\2vR(2T1-T1)+3\2vR(4T1-2T1)=72\2vRT1 (12)
Из (8) vRT1=2\69Q, тогда Q1=24\23Q.

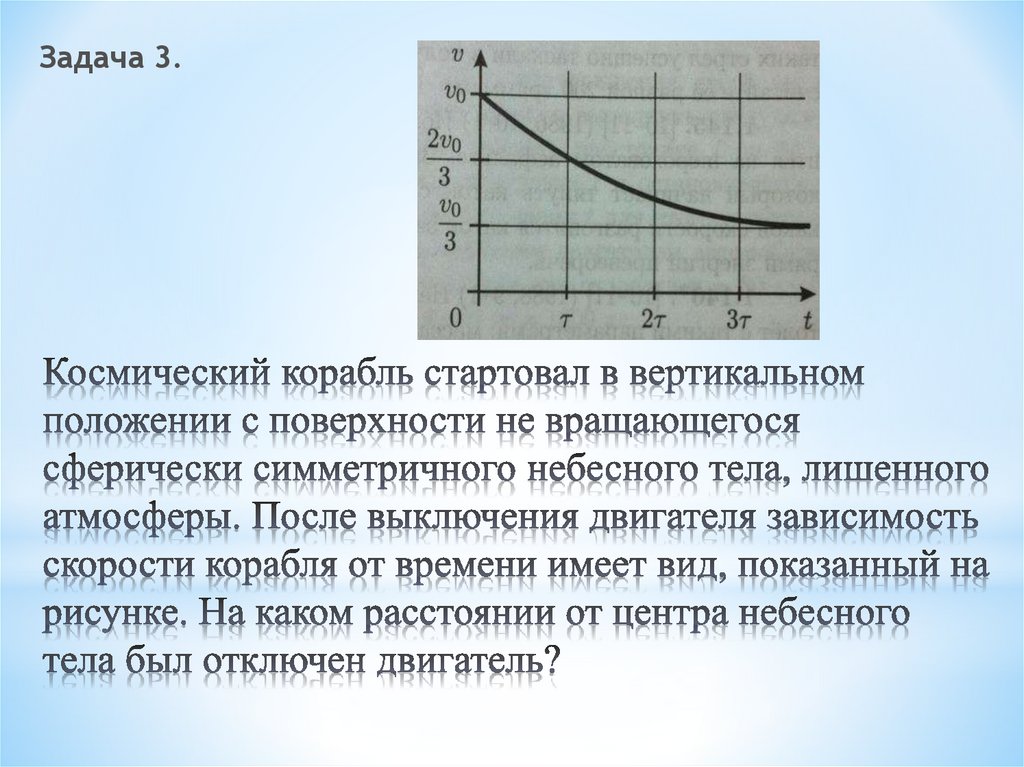
10. Космический корабль стартовал в вертикальном положении с поверхности не вращающегося сферически симметричного небесного тела,

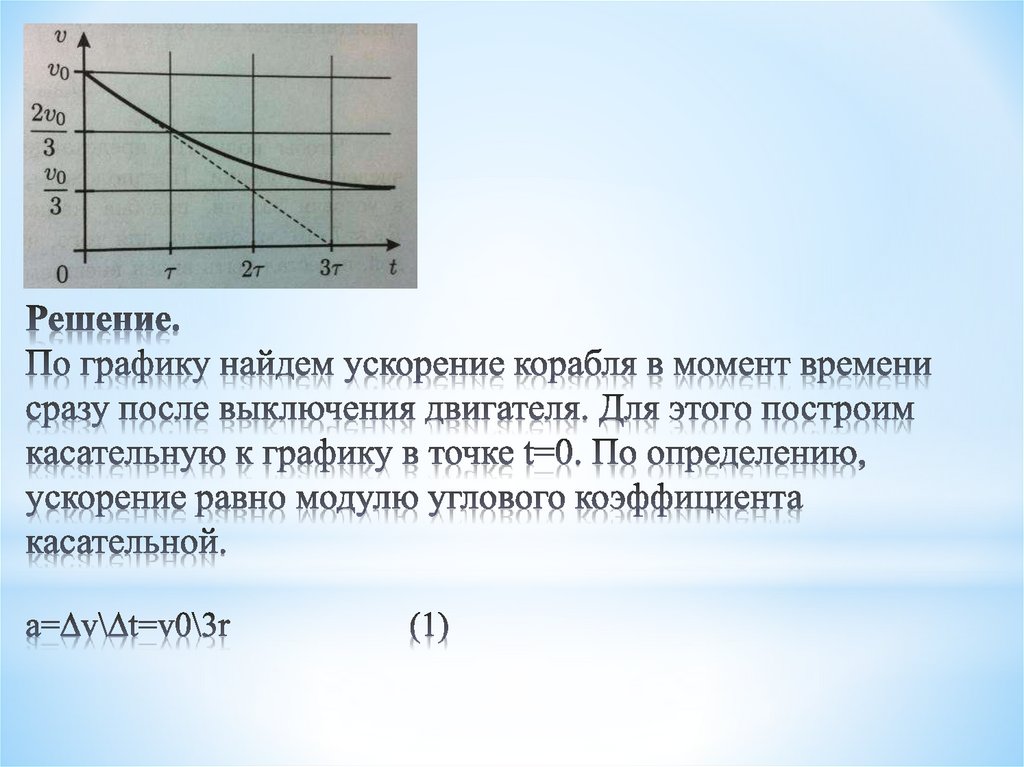
Задача 3.

11. Решение. По графику найдем ускорение корабля в момент времени сразу после выключения двигателя. Для этого построим касательную

12.

После отключения двигателя на корабль действует только
гравитационная сила со стороны небесного тела
ma=GmM\ R2 ,
(1)
Где m и M – масса корабля и масса небесного тела,
R – искомое расстояние.
После удаления корабля на очень большое расстояние от
небесного тела. Его скорость стала постоянной и равна
v1=v0\3.
(3)
Применим закон сохранения механической энергии для
корабля, находящегося в гравитационном поле планеты
mv12 \2-mv02 \2=-GmM\R2 (4)
С учетом (2) перепишем (4) mv12 \2-mv02 \2=-maR (5)
Из (5) и (1) получим
R=(v02 –v12 )\2a=3r\2v0 (v02 -v02 \9)=4\3rv0

13.

Задача 4.
Длинный цилиндрический проводник, по которому
идет электрический ток, охлаждается потоком
жидкости. Во сколько раз изменится перепад
температуры на границе проводник-жидкость, если
радиус проводника увеличить в два раза, не изменяя
его длину и приложенное к нему напряжение?
Считать, то теплоотдача пропорциональна перепаду
температур, а удельное сопротивление материала
проводника не зависит от температуры.

14.

Решение
Количество теплоты, которое выделяется на стержне
Q=(U2 \R)∆t
(1)
Увеличим радиус проводника в два раза r1=2r, тогда
сопротивление R1=ρl\S=ρl\π(r1)2=ρl\4πr2 =R\4 –
уменьшилось в 4 раза
(2)
Площадь поверхности S1=2πr1h=4πrh=2S-увеличилась
в два раза.
Теплоотдача по условию пропорциональна перепаду
температур, следовательно Q\S ∆t =α∆T, где αкоэффициент пропорциональности.
(4)
Тогда Q1\S1∆t=α∆T1
(5)

15.

Учтем (1) и (2) Q1=4Q
(6)
Тогда из (6), (5), (3) получим
Q1\S1∆t=α∆T1=4Q\S∆t=2Q\S∆t=U2\RS
Перепишем (4) Q\S∆t=α∆T=U2\RS
(7)
(8)
Поделим (7) на (8) α∆T\α∆T1=(U2\RS)\(2U2\RS)1\2,
тогда ∆T1=2∆T.
Ответ: перепад температур увеличится в два раза