Similar presentations:
Иррациональные числа
1. Иррациональные числа
Алгебра - 8 класс2.
1) Натуральные числа – это числа,которые используются для счёта
предметов: 1, 2, 3, 4… .
натуральных
2) N-множество
Множество, состоящее
из всех
натуральных чисел, противоположным
чисел,
им отрицательных
чисел и числа нуль
называется множеством целых
Z –множество целых чисел,
чисел.
3) Множество, состоящее из всех
Q
–множество
рациональных
целых и дробных чисел называется
множеством рациональных чисел.
Вспомним:
чисел?
3. Вычислите:
1 2;
3
2
3
7
2 2
;
5
2
;
8
9
;
2 2
.
15
4. Вычислите:
36 ;1
;
144
0,64 ;
16
;
225
1
;
9
4
;
81
0,0004; 1,21.
5. Решите задачу:
Найти площадь квадрата,сторона которого равна 2 .
2
2
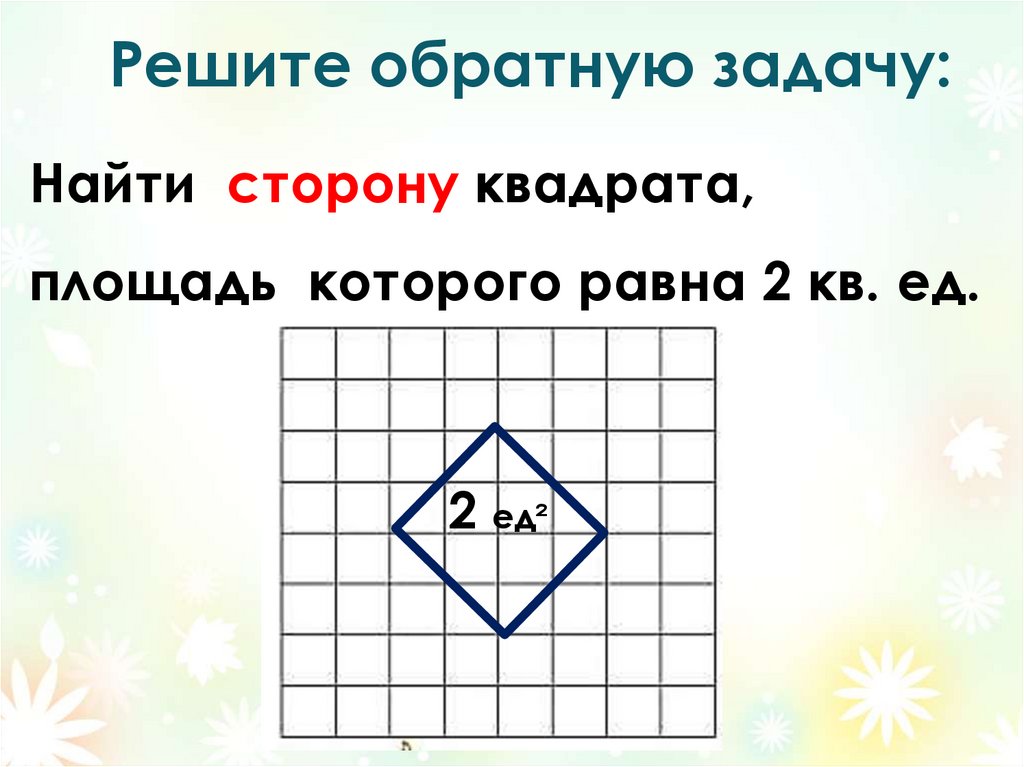
6. Решите обратную задачу:
Найти сторону квадрата,площадь которого равна 2 кв. ед.
2 ед²
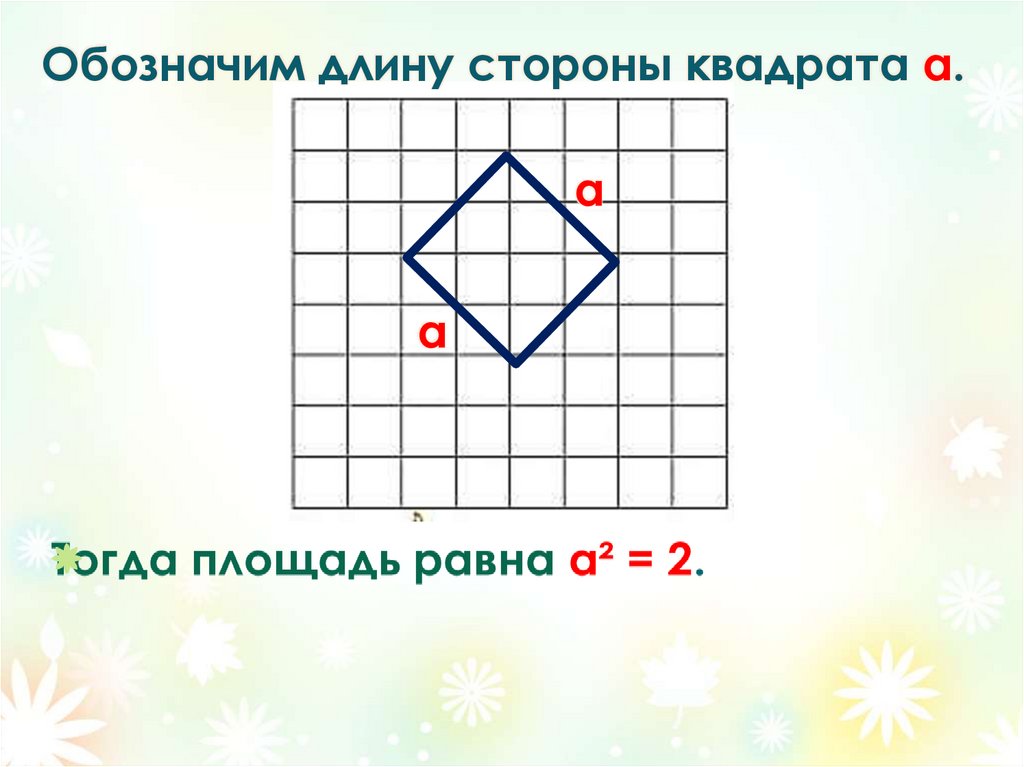
7. Обозначим длину стороны квадрата а.
аа
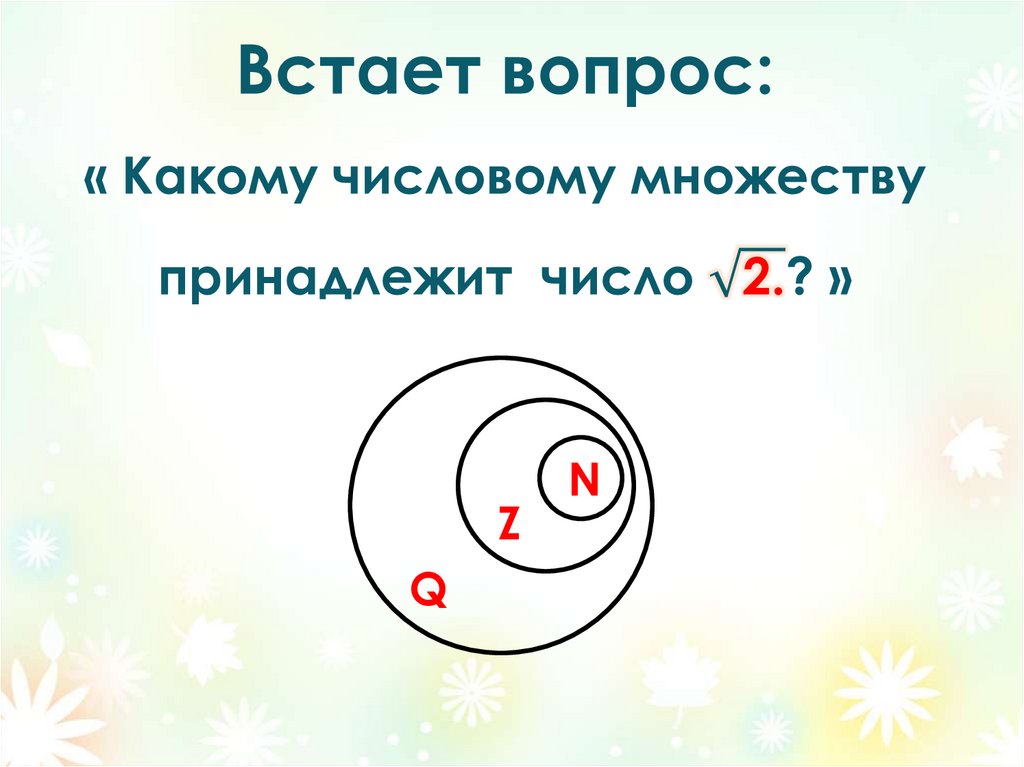
8. Встает вопрос: « Какому числовому множеству принадлежит число √("2." )? »
ZQ
N
9.
10.
11.
12.
13.
Нет ни целого, ни дробногочисла, квадрат которого
равен 2.
14.
Более двадцати веков тому назад к этомувыводу пришли математики Древней Греции,
что вызвало кризис в математической науке:
сторона у квадрата есть, а длины у неё нет!
Но математики нашли выход и из этой
ситуации : раз имеющегося запаса чисел –
целых и дробных – не хватает для выражения
длин отрезков, значит, нужны новые числа.
15.
16. Тема урока
Иррациональные числа.17.
18.
Иррациональные числа появляются нетолько в связи с извлечения квадратных
корней. Существует бесконечное много
иррациональных чисел и другого
происхождения.
Например:
≈ 3, 14…
С= d, S = r²
19.
20.
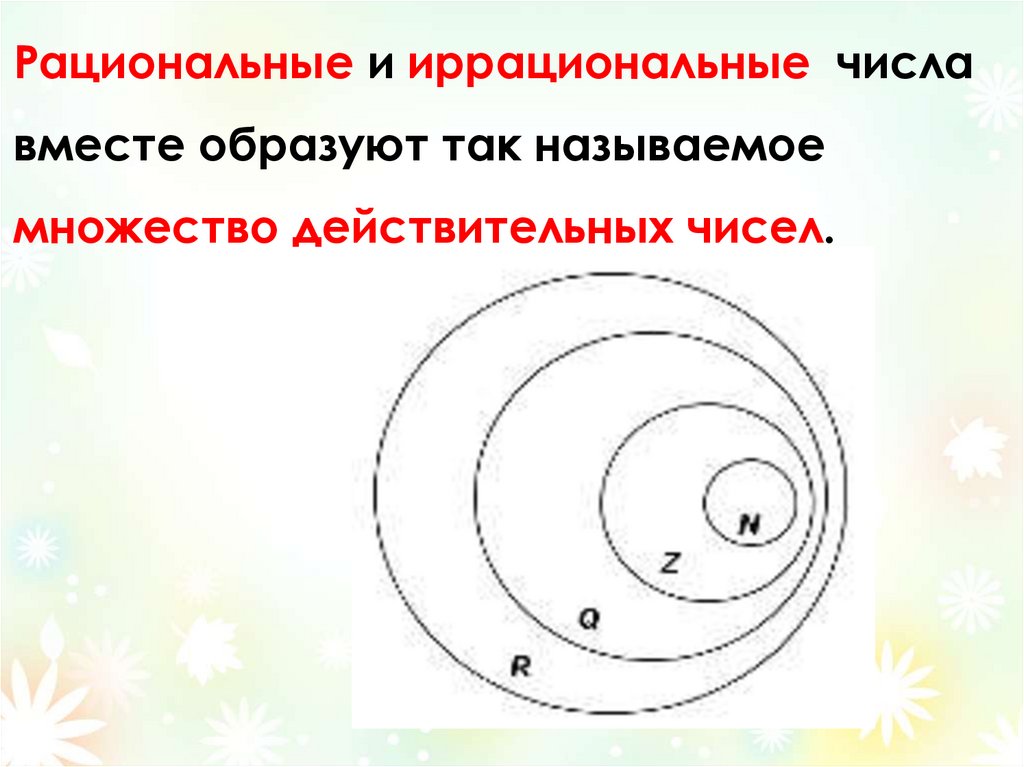
Рациональные и иррациональные числавместе образуют так называемое
множество действительных чисел.
21. Работаем с учебником стр. 74 – 75.
№ 247(устно),№ 248 (а), № 249(а, в, д), № 251, № 252,
№ 253, № 255, № 257, № 258.
22.
23. Домашнее задание.
Прочитать, разобратьи выучить основные понятия
из n 2. 2 . Решить задания:
№ 248(б), № 249 (б, г, е), № 250,
№ 254, № 256.



















 mathematics
mathematics








