Similar presentations:
Иррациональные числа
1. Устно
УСТНО3
1
2
1) -8; 2,1; 7; ; 3,(6); 0; 201;
; -1; 4,2(32)
19
3
1
2
2)
; - 3,25;
9
5
1
1
3) 0,125 и 0,038; -2,45 и -2,54;
и
;
7
3
5,73 и 5,(73); -1,53 и -1,(53); -1,(53) и -1,(35)
4) округлить 13, 509276
2.
ИРРАЦИОНАЛЬНЫЕ ЧИСЛА3.
ОВ 2с точностью до 1
ОВ 2,3 с точностью до 0,1
4.
Результатдесятичного
измерения
На каком-то
шаге не
получится
остатка
Остатки будут
получаться на
каждом шаге
Натуральное
число или
десятичная
дробь
Бесконечная
десятичная
дробь
Бесконечная десятичная дробь
5.
6.
При десятичном измерении отрезка ОК получитсябесконечная десятичная дробь, которая не является
периодической. Это объясняется тем, что среди
рациональных чисел нет такого числа, квадрат
которого равен 2.
7.
Десятичное измерение длин отрезков каждойточке координатной прямой, лежащей справа
от начальной точки О, ставит в соответствие
положительную бесконечную десятичную
дробь. Наоборот, взяв произвольную
положительную бесконечную десятичную
дробь, можем найти на координатной прямой
справа от точки О единственную точку А,
такую, что длина отрезка ОА выражается этой
дробью.
8.
Если к положительным бесконечнымдесятичным дробям присоединить
противоположные им числа и число нуль, то
получится множество чисел, которые называют
действительными числами.
9. Обозначение
ОБОЗНАЧЕНИЕR – множество действительных чисел (от лат.
Realis – реальный, существующий в
действительности)
10.
Числа, которые не являются рациональными, то есть неявляются ни целыми, ни представимыми в виде
дроби вида
m
, где m – целое число, а n – натуральное,
n
называются иррациональными.
I – множество иррациональных чисел
Изученные множества чисел обозначаются следующим
образом:
N – множество натуральных чисел;
Z – множество целых чисел;
Q – множество рациональных чисел;
I – множество иррациональных чисел;
R – множество действительных чисел.
11.
Бесконечнаядесятичная дробь
Периодическая
Непериодическая
Рациональные
числа
Иррациональные
числа
m
n
(«ир»«отрицание»)
Действительные числа R
12.
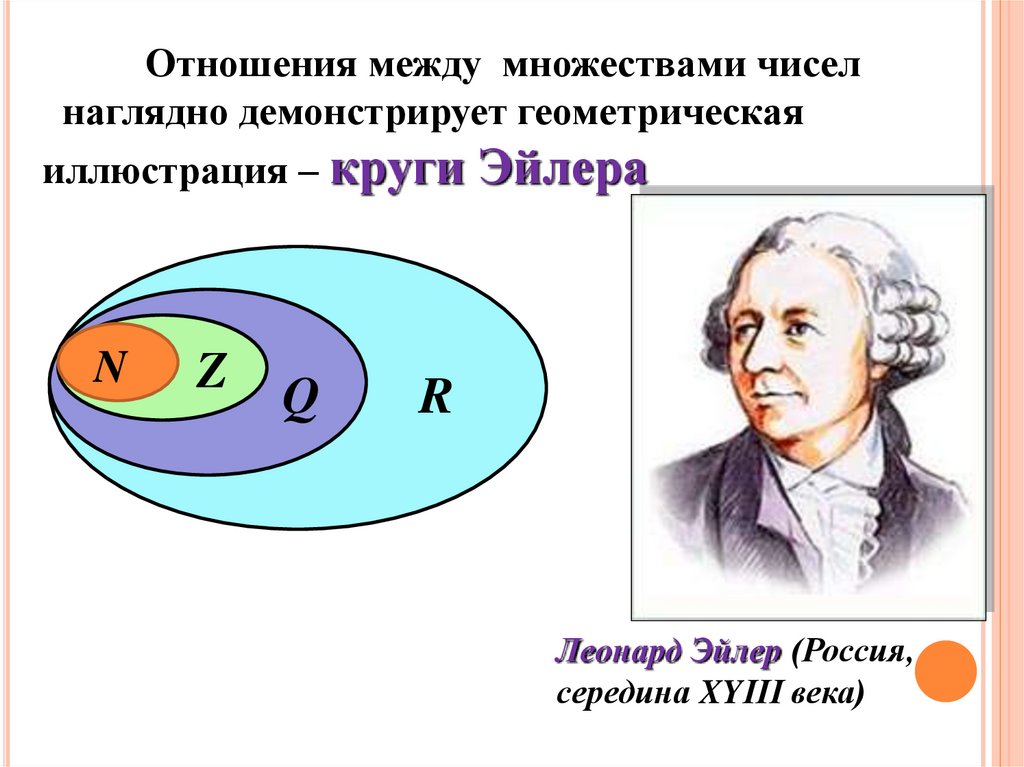
Отношения между множествами чиселнаглядно демонстрирует геометрическая
иллюстрация – круги Эйлера
N
Z
Q
R
Леонард Эйлер (Россия,
середина XYΙΙΙ века)
13. Примеры иррациональных чисел:
ПРИМЕРЫ ИРРАЦИОНАЛЬНЫХ ЧИСЕЛ:3,010010001…
-5,020022000222…
Число
= 3,1415926…, выражающее
отношение длины окружности к диаметру.
14. Действия над действительными числами обладают теми же свойствами, что и действия над рациональными числами: сравнение,
ДЕЙСТВИЯ НАД ДЕЙСТВИТЕЛЬНЫМИЧИСЛАМИ ОБЛАДАЮТ ТЕМИ ЖЕ СВОЙСТВАМИ,
ЧТО И ДЕЙСТВИЯ НАД РАЦИОНАЛЬНЫМИ
ЧИСЛАМИ: СРАВНЕНИЕ, СЛОЖЕНИЕ,
ВЫЧИТАНИЕ, УМНОЖЕНИЕ, ДЕЛЕНИЕ (ЕСЛИ
ДЕЛИТЕЛЬ НЕ РАВЕН НУЛЮ)
2,36366…< 2,37011…
0,253… > -0,149…













 mathematics
mathematics








