Similar presentations:
Рациональные числа. Действительные числа (8 класс)
1.
РАЦИОНАЛЬНЫЕ ЧИСЛА.ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.
2.
Для счета предметов используются числа, которыеназываются натуральными.
Для обозначения
множества натуральных чисел употребляется
буква N - первая буква латинского слова Naturalis «естественный», «натуральный»
N - натуральные
1, 2, 3, 4, 5, …
3.
Числа,им противоположные
-6
-5
-4
-3
-2
-1
Натуральные числа
1 2 3 4 5 6
Z
Целые
4.
Натуральные числа, числа им противоположные ичисло нуль, образуют множество целых чисел,
которое обозначается Z - первой буквой немецкого
слова Zahl - «число».
…, -3, -2, -1, 0,
Z - целые
1, 2, 3, …
5.
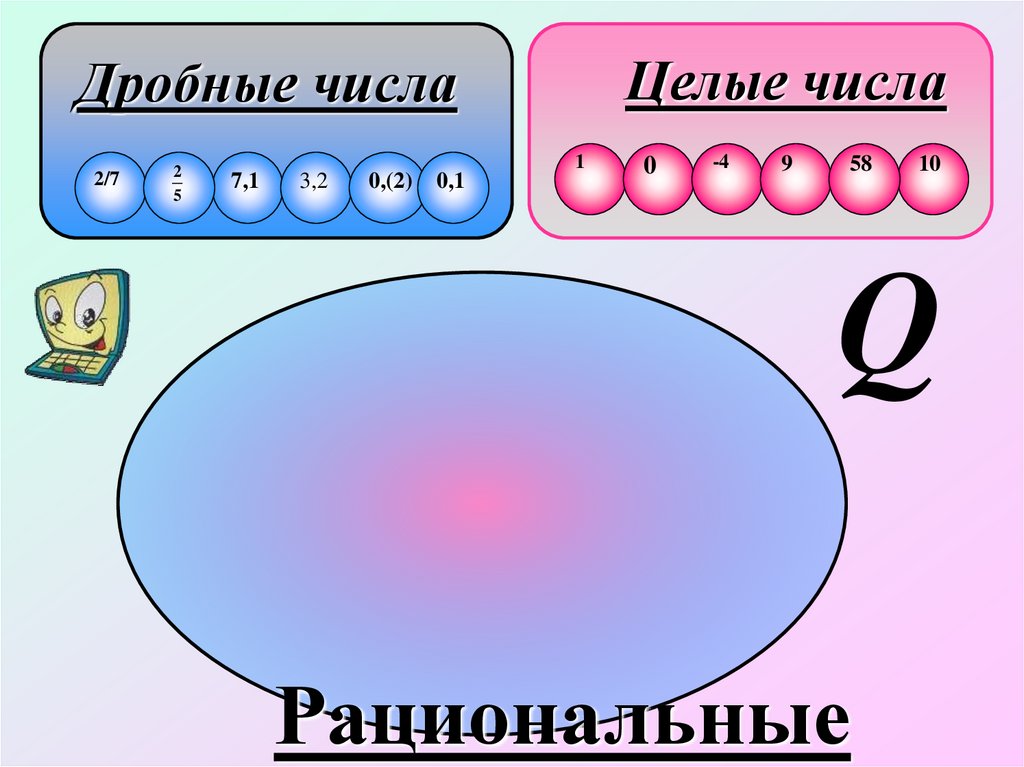
Целые числаДробные числа
2/7
2
5
7,1
3,2
0,(2)
0,1
1
0
-4
9
58
10
Q
Рациональные
6.
Множество чисел, которое можно представить вm
виде
, называется множеством рациональных
n
чисел и обозначается буквой Q - первой буквой
французского слова Quotient - «отношение». Есть
также версия, что название рациональных чисел
связано с латинским словом ratio – разум.
…, -3, -2, -1, 0, 1, 2, 3, …
Q - рациональные
+ дроби
7.
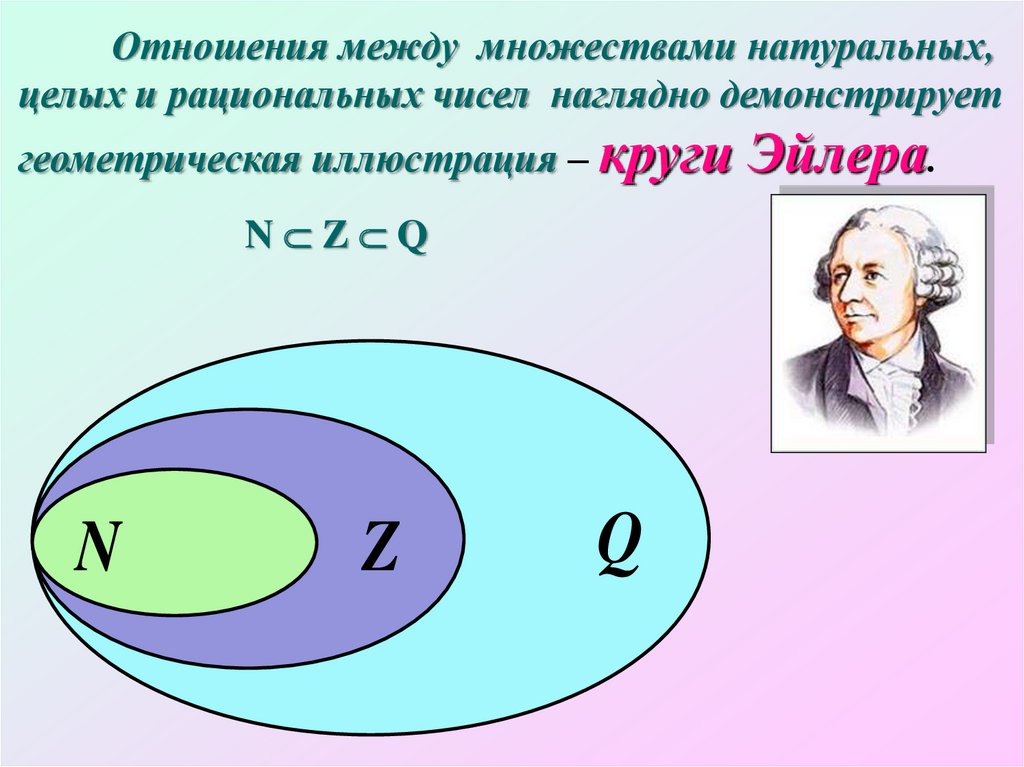
Отношения между множествами натуральных,целых и рациональных чисел наглядно демонстрирует
геометрическая иллюстрация – круги
N Z Q
N
Z
Q
Эйлера.
8.
Математический символ ∈ называют знакомпринадлежности (элемент принадлежит множеству).
«n - натуральное число»
можно писать n ∈ N
«m - целое число»
можно писать m ∈ Z
«r - рациональное число»
можно писать r ∈ Q
9.
Математический символ ⊂ называют знакомвключения (одно множество содержится в другом).
«N - часть множества Z»
можно писать N ⊂ Z,
«Z - часть множества Q»
можно писать Z ⊂ Q
10.
Множества обозначают большими буквами,элементы множества - маленькими буквами.
«x не принадлежит множеству X»
можно писать x ∉ X
«A не является частью (подмножеством) B»
можно писать A B.
11.
N Z QЧисло 5 - ?
N, Z, Q
Число -7 - ?
Z, Q
Число -6,7 - ?
Z, Q
Число
8
19-
?
Q
12.
Любое рациональное числоможно записать в виде
бесконечной десятичной
периодической дроби?
13. Иррациональные числа
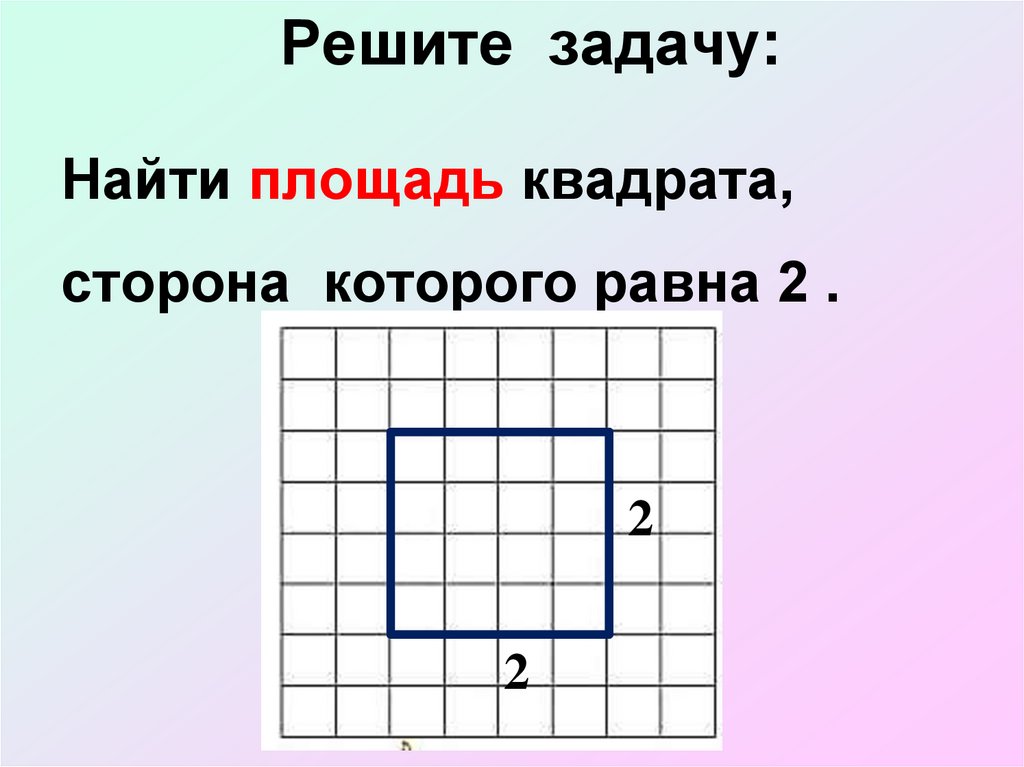
14. Решите задачу:
Найти площадь квадрата,сторона которого равна 2 .
2
2
15. Решите обратную задачу:
Найти сторону квадрата, площадькоторого равна 2 кв. ед.
2 ед²
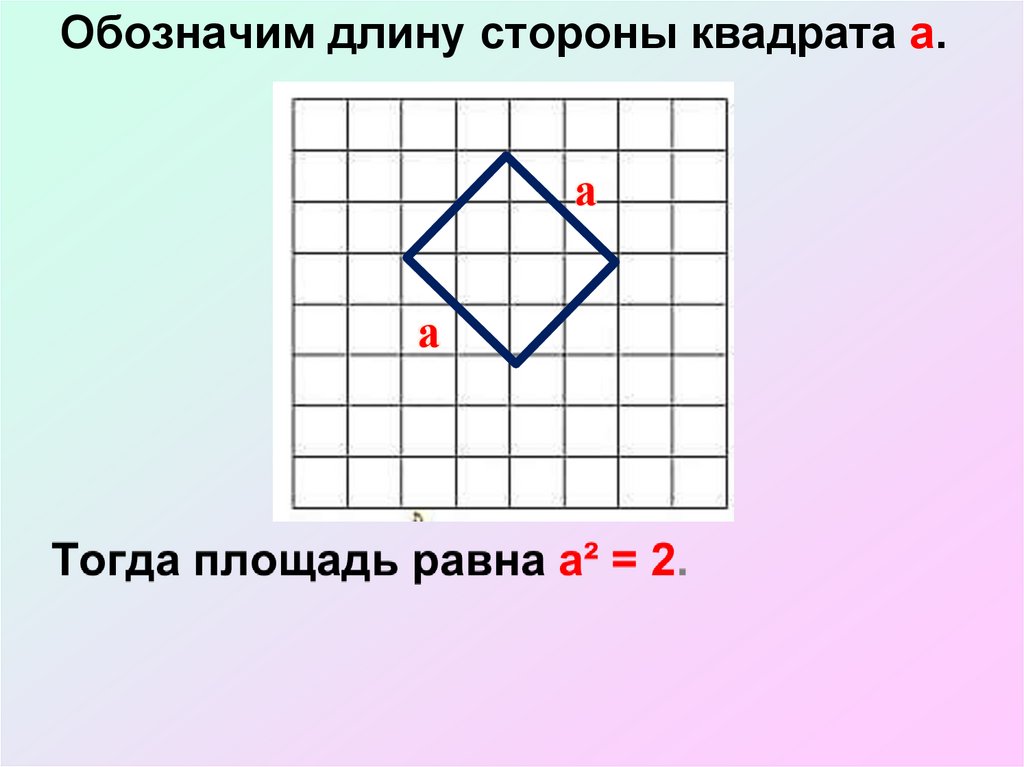
16. Обозначим длину стороны квадрата а.
аа
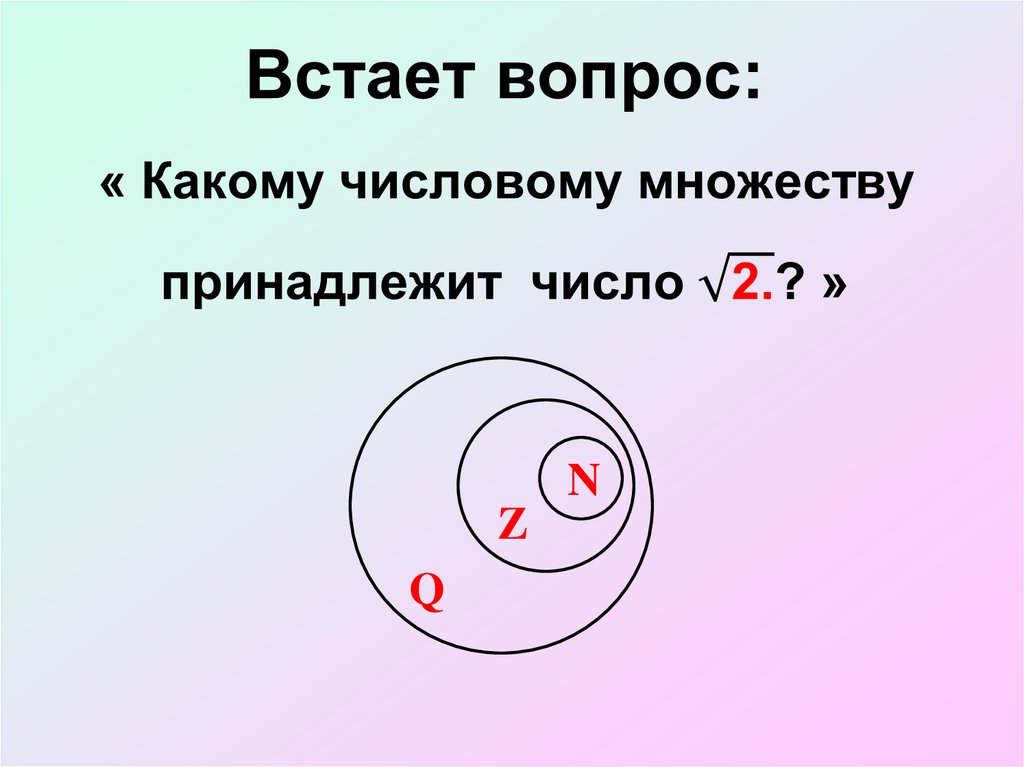
17. Встает вопрос: « Какому числовому множеству принадлежит число √("2." )? »
NZ
Q
18.
19.
20.
Нет ни целого, ни дробногочисла, квадрат которого
равен 2.
21.
Более двадцати веков тому назад к этомувыводу пришли математики Древней Греции,
что вызвало кризис в математической науке:
сторона у квадрата есть, а длины у неё нет! Но
математики нашли выход и из этой ситуации :
раз имеющегося запаса чисел – целых и
дробных – не хватает для выражения длин
отрезков, значит, нужны новые числа.
22.
23.
24.
Иррациональные числа появляются нетолько в связи с извлечения квадратных
корней. Существует бесконечное много
иррациональных чисел и другого
происхождения.
Например:
≈ 3, 14…
С= d, S = r²
25. Иррациональные числа
Бесконечнаянепериодическая дробь
называется
иррациональным
числом.
Например:
Множество иррациональных
чисел обоначается J.
26.
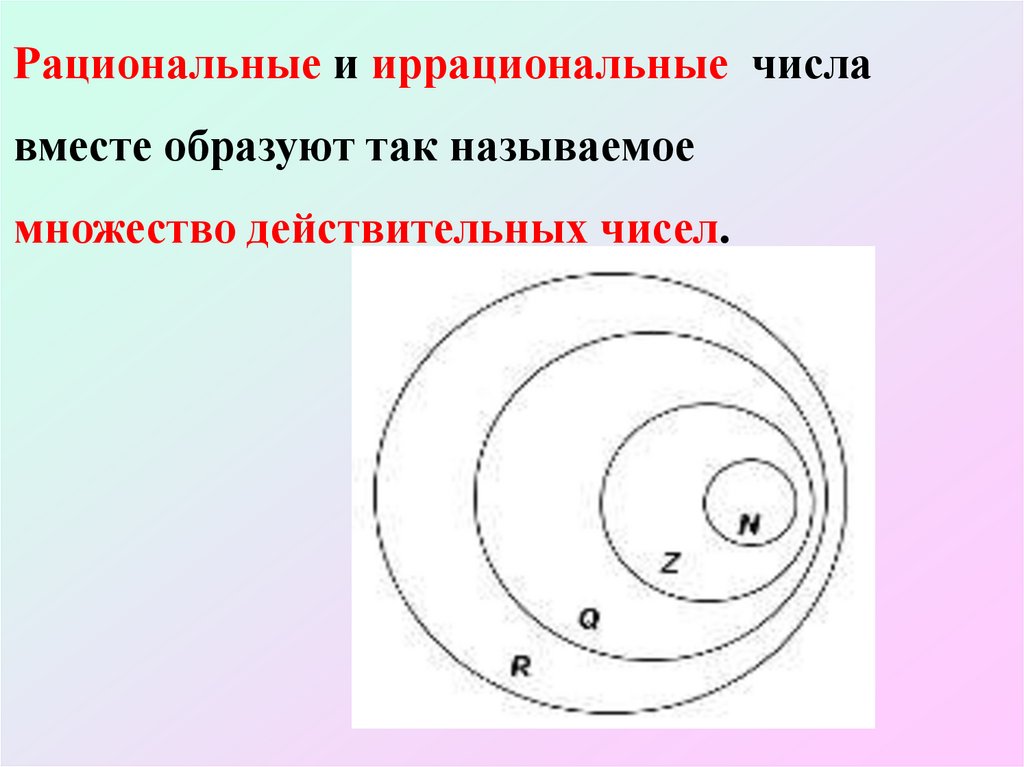
Рациональные и иррациональные числавместе образуют так называемое
множество действительных чисел.





















 mathematics
mathematics








