Similar presentations:
Электромагнитная природа света. Интерференция света
1. Лекция № 12-13 (окончание)
ЭЛЕКТРОМАГНИТНАЯПРИРОДА СВЕТА.
ИНТЕРФЕРЕНЦИЯ СВЕТА
Литература: Павлов К.Б. Волновые
свойства света. Учебное пособие. – М.:
МВТУ, 1986, Иродов И.Е. Волновые
процессы. Основные законы. – М. – С.-П.:
Физматлит, 1999.
2.
Интерференция света в тонкихпленках
Интерференционные полосы равной
толщины и равного наклона
Интерференционные полосы равного
наклона
возникают
при
отражении
параллельных
пучков
света
от
плоскопараллельных
пленок.
Интерференционные полосы равной
толщины возникают при отражении пучков
света от пленок, толщина которых не
постоянна.
3.
Полосы равной толщины и равного наклонамогут наблюдаться при прохождении
указанных пучков света через пленки.
Попадая на границу раздела сред э/м
волны частично отражаются, частично
преломляются.
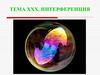
Если n2 > n1, то отражение волны
сопровождается потерей полуволны E (фаза
его колебаний изменяется на π). Если
n2 < n1,
потеря полуволны происходит у H
4.
EH
n1 n2
n1 n2
v
v
E
H
n1 n2
n1 n2
v
E H
v
H
E
Выражение оптической разности хода Δ
должно быть дополнено слагаемым λ/2. Знак
перед λ/2 выбирается из соображений
удобства.
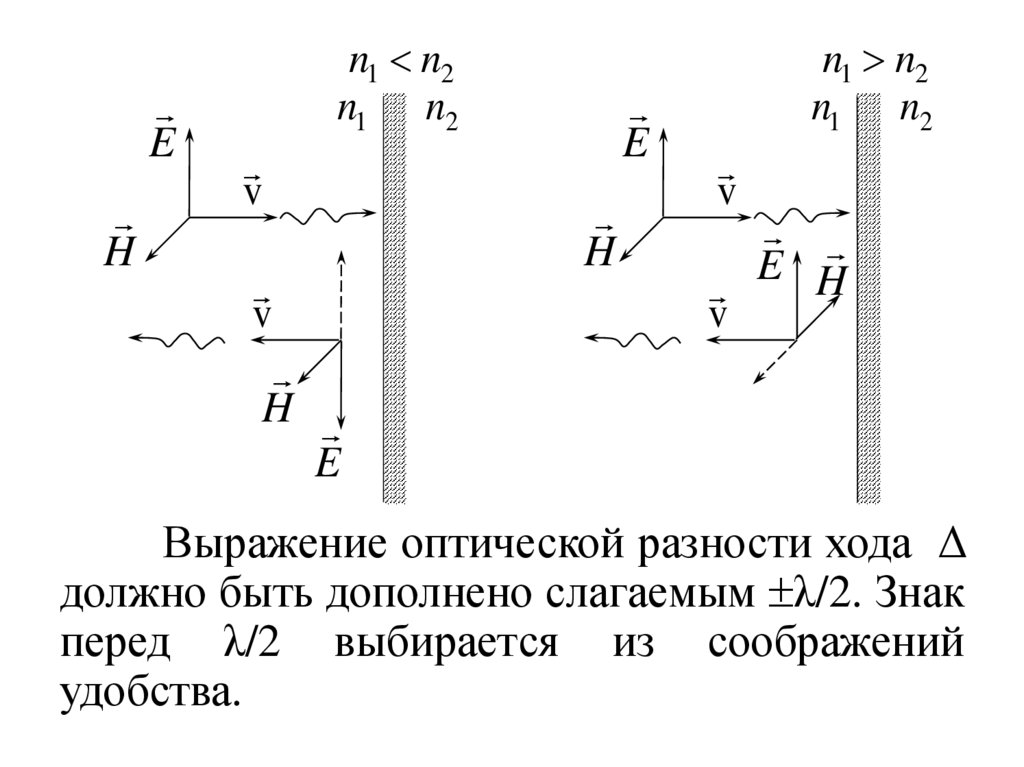
5. Интерференция в тонких пластинах (пленках)
Пластина постоянной толщины, однородная1
2
i
D
i
d
1
2
i
C
A
r
B
n
6.
Оптическая разность ходаAB BC n DC 2
d
AB BC
cosr
DC AC sin i 2 BC sin r sin i
DC 2d tg r sin i
Подставим (13.2) и (13.3) в (13.1)
2dn
2d tg r sin i
cos r
2
(13.1)
(13.2)
(13.3)
7.
sin in,
sin r
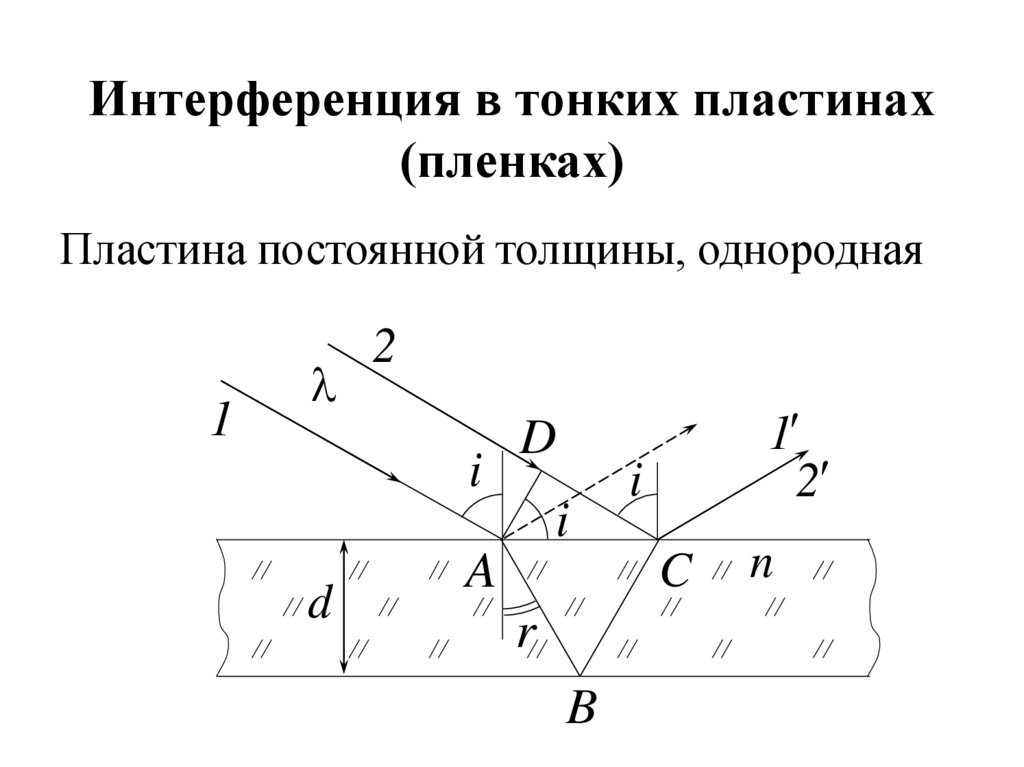
С учетом
(13.4)
1 sin i n
2dn
cos r
2
2
Из (13.4)
2
(13.5)
2
sin i
sin r 2
n
2
или
2
sin i
cos r 1 sin r 1 2
n
2
2
(13.6)
8.
Подставив (13.6) в (13.5)2dn cos r 2
или, с учетом (13.6)
2d n sin i 2
2
2
Условие максимума
2d n sin i 2m
2
2
(13.7)
2d n sin i 2m 1
2
2
(13.8)
2
2
Условие минимума
2
2
9. Тонкий клин (с малым углом при вершине)
Условие максимума для луча 11
2
l
max
2d1n 2 m
(13.9)
Условие максимума для луча 2
d1 2d n 2 m a (13.10)
2
Вычтем из (13.10) (13.9)
2 d 2 d1 n a
d2
n
2nl tg a (13.11)
10.
Пусть клин стеклянный n = 1, l = 10-2 м,a = 5, λ 5 10-7 м (зеленый свет). Тогда,
используя (13.11)
7
5
5
10
a
5
8
,
3
10
,
tg
2
2nl 2 1,5 10
угол получается в секундах.
Если взять толстый клин (α ~ нескольких
градусов), то максимумов будет больше; они
могут быть неразличимы глазом (сливаются).
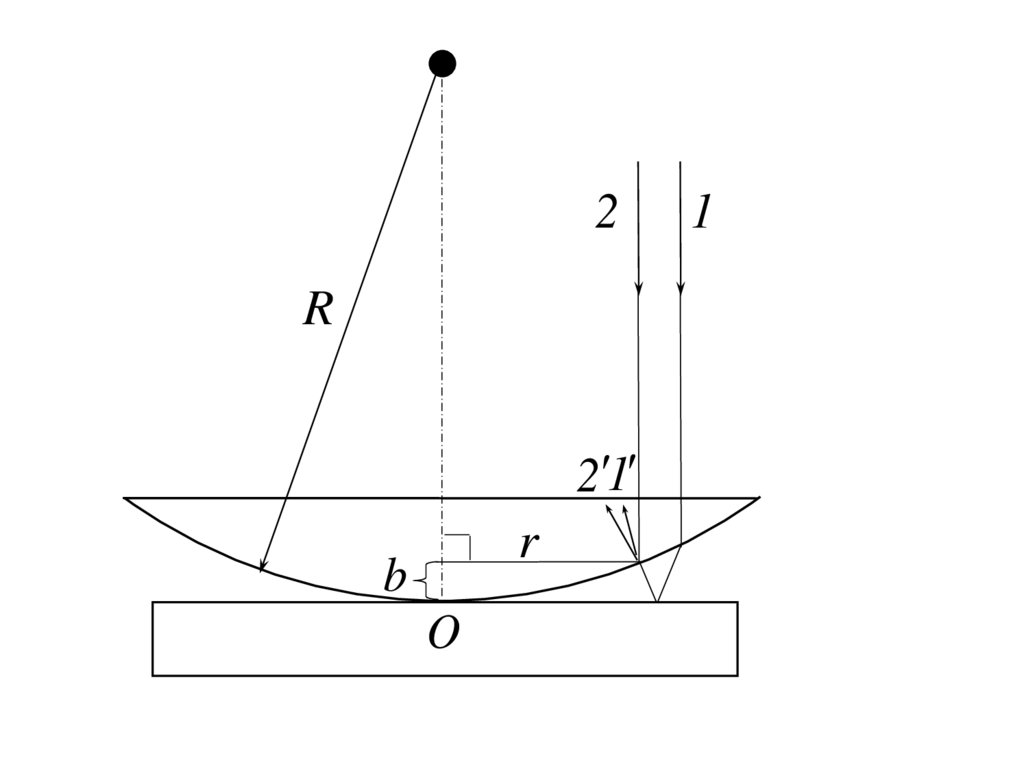
11. Кольца Ньютона
– полосы равной толщины, возникающие врезультате интерференции света в воздушном
зазоре, образованном при соприкосновении в
т. O плосковыпуклой линзы малой кривизны
с плоской стеклянной поверхностью. При
использовании
источника
монохроматических волн полосы равной
толщины представляют собой систему
концентрических темных и светлых колец,
расположенных вокруг темного круга с
центром в т. O (наблюдение проводится в
отраженном свете).
12.
2R
2 1
r
b
O
1
13.
Пучок монохроматических лучей сдлиной волны λ падает нормально на
плоскую поверхность линзы (лучи 1 и 2).
r R R b ,
2
2
2
r R R 2 Rb b ,
2
2
2
2
r 2 Rb b .
2
2
Так как b << R, то
r 2bR
2
14.
Радиус кольцаr 2bR
Оптическая
разность
хода
интерферирующих лучей, с учетом «потери»
полуволны при отражении от оптически
более плотной среды (при падении луча из
воздуха на стекло):
2b
2
15.
Для светлого кольца:2b m ,
2
m 1,2,3,
откуда
1
2b m , m 1,2,3,
2
Радиус m-ого светлого кольца
1
rm m R ,
2
m 1,2,3,
(13.12)
16.
Для темного кольца:2b 2m 1 ,
2
2
m 0,1,2,
m 0,1,2,
откуда
2b m ,
Радиус m-ого темного кольца
m 0,1,2, (13.13)
rm m R ,
m=0 соответствует минимум темного пятна.
Если в зазор поместить жидкость с
показателем преломления n (n < nст.) , то
2bn
2
и т.д.
17. Применение интерференции
Просветлениеоптики.
При
прохождении
света
через
каждую
преломляющую
поверхность
линзы
отражается примерно 4% падающего света. В
сложных объективах такие отражения
совершаются многократно и суммарная
потеря светового потока оказывается весьма
ощутимой. Например, в призменном бинокле
она составляет свыше 50%.
18.
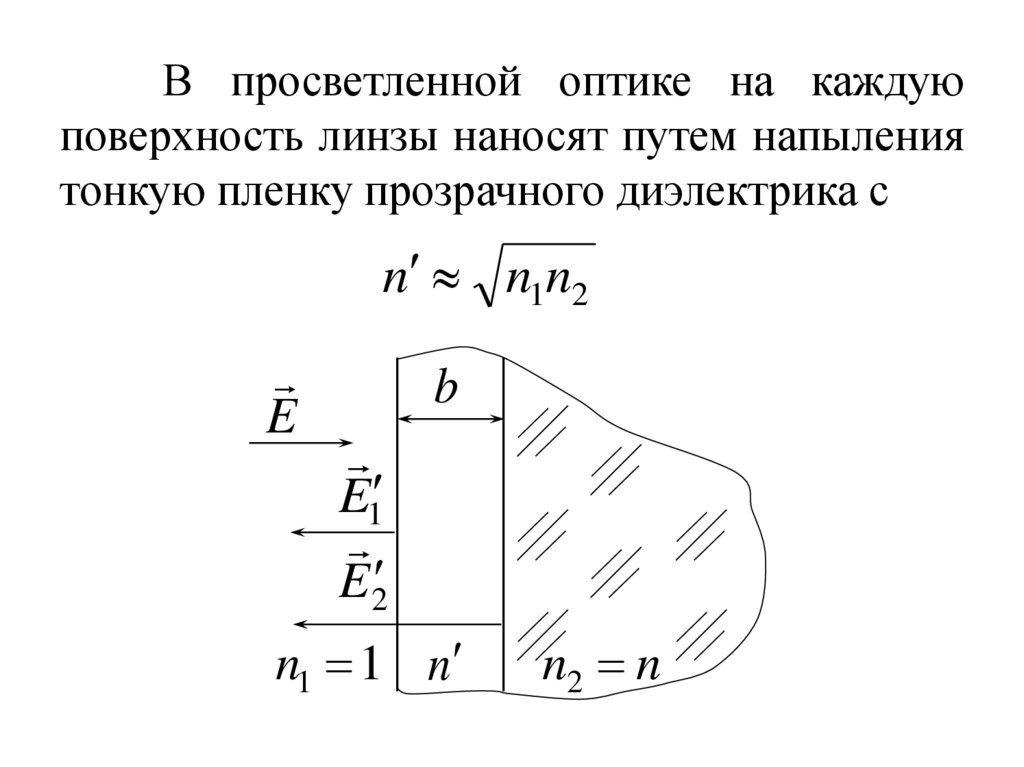
В просветленной оптике на каждуюповерхность линзы наносят путем напыления
тонкую пленку прозрачного диэлектрика с
n n1n2
E
b
E1
E2
n1 1 n
n2 n
19.
Приэтом
условии
амплитуды
отраженных от обеих поверхностей пленки
волн оказываются практически одинаковыми.
При
E1 E 2
E1 E2
E
E
(13.14)
Из рассмотрения отражения и преломления
плоской волны на границе двух диэлектриков:
n1 n2
E x
Ex
n1 n2
(13.15)
20.
с учетом (13.14) и (13.15)При
n1 n n n2
n1 n n n2
n2 n
n1 1,
1 n n n
n n
1 n n n
Толщина пленки делается такой, чтобы
волны, отраженные от обеих поверхностей
пленки, оказывались в противофазе, т.е.
гасили друг друга.
21.
Определим толщину пленки для этогослучая. Оптическая разность хода этих двух
отраженных волн на выходе из пленки
2bn 2m 1 , m 0,1,2,...
2 2
2
2bn 2m 1 , m 0,1,2,...
2
Определим толщину тонкой пленки:
b
2m 1 2m 1
,
4n
4 n
m 0,1,2,...
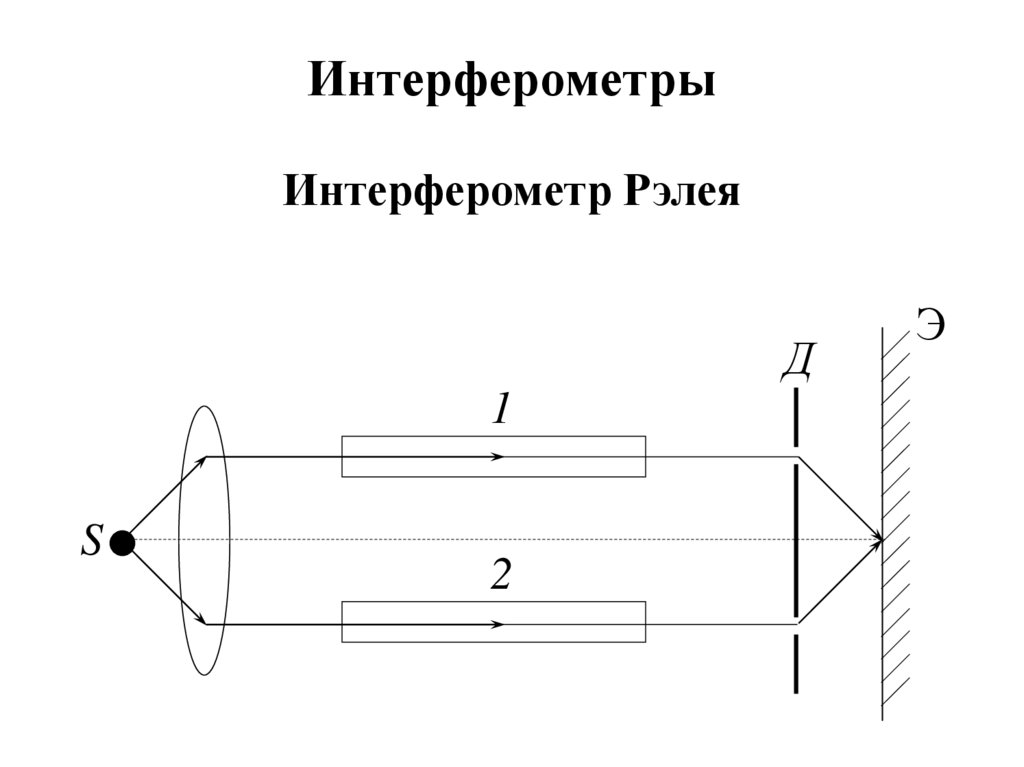
22. Интерферометры
Интерферометр РэлеяД
1
S
2
Э
23.
На схеме S – узкая щель, освещаемаямонохроматическим светом с длиной волны
λ, 1 и 2 – две одинаковые трубки с воздухом,
длина каждой из которых равна l, торцы –
прозрачные, Д – диафрагма с двумя щелями.
Когда воздух в трубке 1 постепенно заменили
газом X, то интерференционная картина на
экране Э сместилась на N полос. Зная
показатель
преломления
n0
воздуха,
определяют показатель преломления газа X.
Смещение на N полос означает, что
оптическая разность хода Δ лучей, падающих
на щели, стала равной Nλ:
l n l n0 N
24.
Отсюда показатель преломления газа Xn n 0 N l
Смещение полос вверх свидетельствует о
том, что и максимум нулевого порядка
сместился вверх. При этом увеличение
геометрической длины луча 2 компенсируется
увеличением оптической длины луча 1.
Интерферометр Рэлея используют для
измерения малых разностей показателей
преломления прозрачных веществ (газов и
жидкостей).


















 physics
physics