Практический критерий Найквиста. Запас устойчивости САР

1. Практический критерий Найквиста. Запас устойчивости САР

Лекция №13
1

2.

На устойчивость САР влияют на устойчивость
влияют
только
переходы,
совершаемые
годографом Wр(jω) на отрезке вещественной
ости (-∞;-1]. Будем считать пересечение
годографом участка вещественной оси сверху
вниз
положительными,
а
снизу
вверх
отрицательными, про возрастании частоты ω
от нуля до бесконечности.
j
∞
0
-1j0
+
+
-
0
∞
2

3.

Формулировка
САР автоматического регулирования будет
устойчива в замкнутом состоянии, если
разность между числом положительных и
отрицательных
переходов
годографом
Wp(jω) участка (-∞;-1] будет равна m/2, где m –
количество правых корней характеристического
уравнения замкнутой системы В(р)=0.
Примечание: в случае наличия нулевых корней
исходный годограф необходимо дополнить на
угол u*π/2.
3

4.

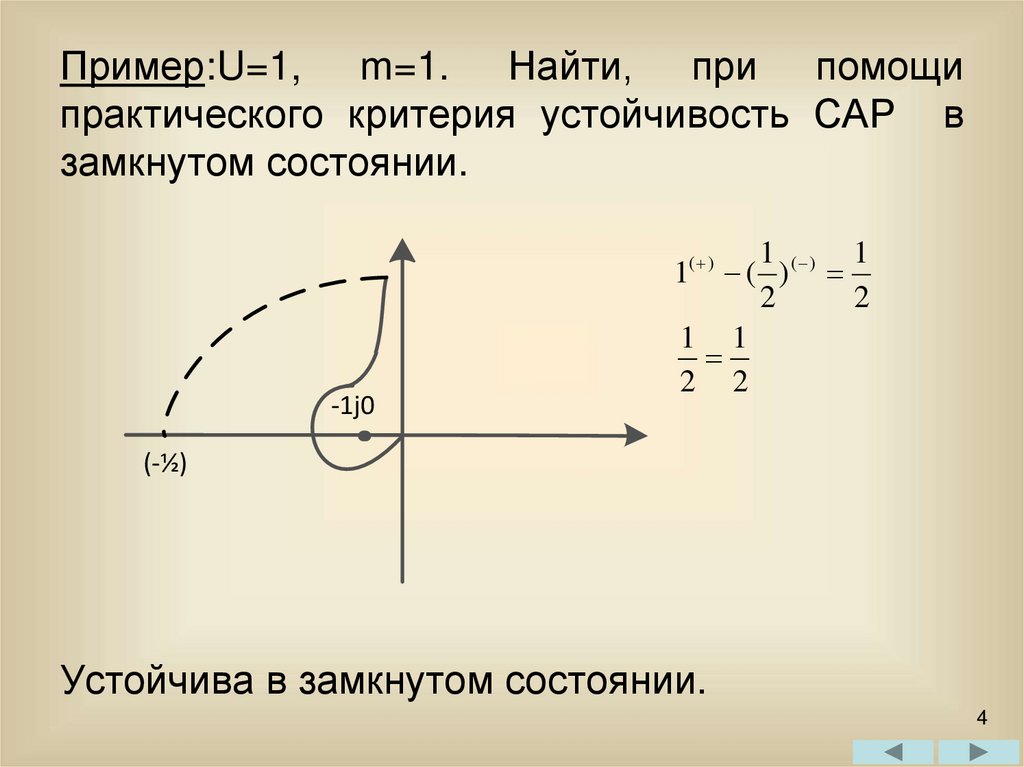
Пример:U=1, m=1. Найти, при помощи
практического критерия устойчивость САР в
замкнутом состоянии.
-1j0
1
1
1( ) ( ) ( )
2
2
1 1
2 2
(-½)
Устойчива в замкнутом состоянии.
4

5.

Практический
критерий
Найквиста
для
логарифмических частотных характеристик
Участку вещественной оси (-∞;-1] соответствует
участок частот, где L(ω)>0.
L(ω)
j
-1j0
+
lgω
Установим соответствия между переходами
годографа
участка
вещественной
оси
и
пересечением ФЧХ прямой - π.
5

6.

j
∞
0
+
+
-
Φ(ω)
0
∞
∞
lgω
0
-π
(+)
(-)
0
+
∞
6

7.

Критерий
САР будет устойчива в замкнутом
состоянии,
если
разность между
числом положительных и отрицательных
переходов ФЧХ при пересечении прямой
-π на участке, где L(ω)>=0, будет равно
m/2, где m – количество правых корней.
Примечание: в случае наличия нулевых
корней ФЧХ исходной системы дополняется
дополняется на угол π/2* ν.
7

8.

Пример: W p ( p)
K
p 2 * (1 pT )
L(ω)
j
-40 дб/дек
-60 дб/дек
ω
+
-π
(-)
Система не устойчива
-(3π/2)
8

9.

Запасы устойчивости
В
процессе
эксплуатации
происходит
изменение параметров системы. Поэтому для
стабильной работы САР необходимо иметь
определенный запас по амплитуде и по фазе.
W p ( j ) 1
arg W p ( j )
Система
будет
находится
только
при
одновременном выполнении условий. При
выполнении
одного
из
условий
будет
устойчива, и в этом случае ищется запас по
другому параметру.
9

10.

Нахождение запаса по фазе
1.Строится годограф Wp(j ω);
2.Проводится окружность радиуса единица.
Точку пересечения с годографом обозначаем А.
Вектор ОА иметь длину равную 1.
( а ) - аргумент Wp(j ω); ( а ) arg W p ( j а )
j
-jω0
B
0
Φ(ω0)
+
Угол АОВ – это угол , на
который нужно довернуть
вектор ОА, что бы система
стала
на
границе
устойчивости.
А
Wp(ju)
10

11.

Угол АОВ= α – запас по фазе, который
определяется:
arg W p ( j a )
Для реальных систем сдвиг по
выбирается не меньше 30 градусов.
фазе
11

12.

Запас по амплитуде
Его определяют при выполнении второго условия,
т.е.: arg W p ( j )
j
-jω0
А
0
+
12

13.

Длина отрезка ОА равна W p ( j ) , запас по
амплитуде определяется соотношением:
1
W p ( j )
Как правило запас по амплитуде определяется в
децибелах, т.е.:
20 lg 20 lg 1 20 lg W p ( j ) 20 lg W p ( j )
Для реальных систем должен быть не меньше 20
дб.
13

14.

Определение
запаса
устойчивости
по
логарифмическим характеристикам
При прохождении у годографом Wp(jω); через
точку -1j0 для логарифмических характеристик
будут выполняться условия:
L( ) 0
( )
При выполнении двух условий система
находится на границе устойчивости.
При выполнении одного система будет
устойчива, и можно найти запас для второго
мапаметра.
14

15.

L(ω)
1.L( п ) 0
зап п ( п )
-20 дб/дек
2. ( п )
-40 дб/дек
ω
1
W p ( j )
-60 дб/дек
Φ(ω)
ω
φзап.
-π
15