Similar presentations:
Критерий Найквиста (лекция №12)
1. Критерий Найквиста
Лекция №121
2.
Пример 1W р ( р)
k
1 рT
j
Wp(jω)
-1j0
K
0
+
0
∞ ω
Система всегда устойчива, так как при
любых параметрах К,Т годограф Wp(jω) не
охватывает точку -1j0, при изменении
частоты от нуля до бесконечности.
2
3.
Пример 2kр
Wр ( р)
(1 рT1 ) * (1 рT2 ) * (1 рT3 )
j
K1
-1,j0
крпр
K2
+
Система будет устойчива до определенного
значения k.
3
4.
Очевидно существует Крпред , где системанаходится на границе устойчивости.
Кр=Крпред,
В этом случае годограф пройдет через точку
(-1,j0,) и система будет находиться на границе
устойчивости.
Крпред можно найти из системы уравнений:
Wp ( j ) 1
arg Wp ( j )
Из второго уравнения находим
в первое и находим Крпред.
, подставляем
4
5.
2. САР неустойчива в разомкнутом видеarg F ( j ) arg H ( j ) arg B( j )
0
0
0
Предположим, что разомкнутая система имеет
характеристический многочлен В(р) степени-n,
причем m правых корней, (n-m) – левых. Для
данного случая изменение аргумента:
arg B( j ) (n m) * 2 m * 2 (n 2m) * 2
0
Нас интересует устойчивость системы в
замкнутом состоянии. Для того что бы она была
устойчива, необходимо и достаточно, что бы все
корни H(р)=0
располагались
в
левой
полуплоскости:
arg H ( j ) n * 2
0
5
6.
arg F ( j ) n *0
2
( n 2 m) *
2
2m *
2
m*n
m
* 2
2
САР
неустойчивая
в
разомкнутом
состоянии, будет устойчива в замкнутом,
если годограф Wp(jω) охватывает в
положительном направлении, точку с
координатами -1,j0, m/2 раз при изменении
ω от нуля до бесконечности. Где m –
количество правых корней B(р)=0.
6
7.
Пример:W p ( p)
K
( 1 PT1 )(1 pT2 )
Найти значение параметров К,Т1, Т2, при
которых
система
будет
устойчива
в
замкнутом состоянии.
B( p) ( 1 pT1 )(1 pT2 ) 0;
p1 1 / T1;
A( )
∞
0
Т1<T2 К
Т1>T2
K
1 ( T1 ) * 1 ( T2 )
2
ω0
2
0
∞
( ) arctg T2 ( arctg T1 )
7
8.
Вывод: при Т2>Т1 годограф Wp(jω) охватываетточку (-1,j0) в отрицательном направлении,
значит САР в замкнутом состоянии будет
неустойчива.
Если годограф начинается и заканчивается на
участке вещественной оси, то будем иметь ½
охвата.
При Т1>Т2, годограф Wp(jω) охватывает точку
(-1,j0) 1/2 раза в положительном направлении.
½=1/2, значит САР в замкнутом состоянии
устойчива.
Вывод: Если К>1 и Т1>Т2, то система будет
устойчива в замкнутом состоянии.
8
9.
3. САР в разомкнутом состоянии на границеустойчивости: Wp ( р) A( р) s
B( р) * р
В общем виде:
где s –степень астатизма САР
Рассмотрим случай, при s=1:
W p ( р)
A( р)
B( р) * р
В данном случае принципы аргумента не
работают, т.к он неприменим при Pi=0.
Для использования принципа необходимо
произвести сдвиг нулевого корня либо в
левую, либо в правую полуплоскость. И
исходная функция ищется как предел вновь
9
полученной функции.
10.
Рассмотримпримере:
данный
случай
на
следующем
K
Wp( р)
р(1 рT1 ) * (1 рT2 )
р1=0;
р2=-1/Т1;
р3=-1/Т2;
Произведем сдвиг нулевого корня в левую
полуплоскость, т.е.: р1=- α;
В этом случае вновь полученная передаточная
функция будет иметь вид:
K
W p ' ( р)
( р) * (1 рT1 ) * (1 рT2 )
А Wp(p) может быть получена в предельном
переходе при α стремящейся к нулю.
W p ( р ) lim W p ' ( р )
a 0
Что бы перейти к стандартной форме нужно
10
поделить числитель и знаменатель на α.
11.
KW p ' ( р)
(1
р
;
) * (1 рT1 ) * (1 рT2 )
где T’=1/ α.
В результате Wp’(p) описывает статическую
систему третьего порядка. Для такой системы
годограф Wp’(p) имеет вид:
j
k/α
-1,j0
Wр(jω)
1
k/α’
+
2
W,р(jω)
11
12.
При уменьшении α годограф Wp’(jω)будет
начинаться
правее
предшествующего
и
следовательно годограф Wp’(jω) будет совпадать
с годографом Wp(jω) практически на всех
частотах, кроме низких частот. В пределе при α=0
оба годографа будут отличаться только на
частоте ω=0 и совпадать на всех других частотах.
Дополнив годограф Wp(jω) дугой бесконечного
радиуса на угол π/2 в положительном
направлении, мы получим годограф Wp’(jω).
Таким образом для анализа устойчивости
необходимо исходный годограф дополнить дугой
бесконечного радиуса на угол π/2.
12
13.
ФормулировкаСАР, имеющая нулевые корни( находящая
на границе устойчивости в разомкнутом
состоянии) будет устойчива в замкнутом,
если годограф Wp(jω) , дополненный дугой
бесконечного радиуса на угол (s*π/2), не
охватывает точку с координатами (-1j0), при
изменении
частоты
от
нуля
до
бесконечности.
13
14.
Пример:W p ( j )
W p ( p)
K
;
2
p (1 pT )
j
K
;
2
( j ) (1 j T )
2;
Wp(j? )
?
0
A( )
K
2 1 ( T ) 2
;
?
-1j0
0
+
( ) arctg T .
Дополненный годограф всегда охватывает
точку (-1,j0), следовательно при любых
параметрах системы она будет неустойчива в
замкнутом состоянии.
14
15.
Анализ устойчивости САР с запаздываниемWp ( р) W1 ( р) * e р
A( р) p
*e
B( р )
H ( р) A( р) * e р B( р)
Алгебраические интерпретации для таких
систем неприемлемы, однако частичные
критерии,
основанные
на
принципе
аргумента можно использовать.
15
16.
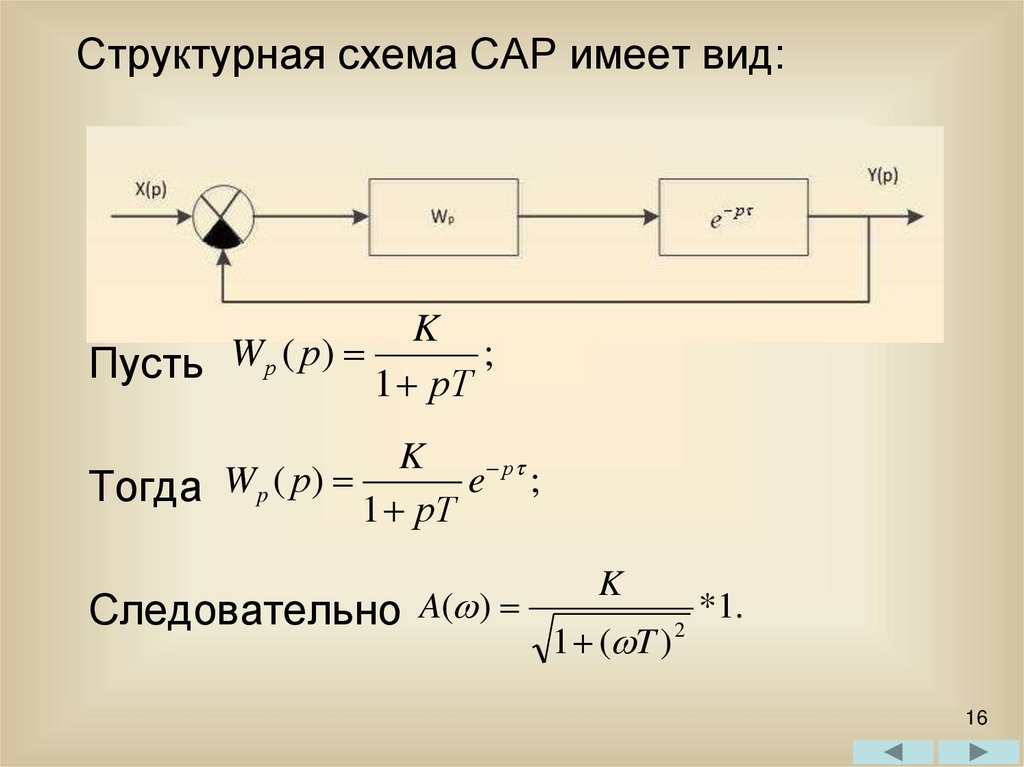
Структурная схема САР имеет вид:K
Пусть W р ( р) 1 рT ;
K
р
W
(
р
)
e
;
Тогда p
1 рT
Следовательно A( )
K
1 ( T )
2
*1.
16
17.
j+
W(jω)
W2r
W2
W1
W1r
Для
построения
годографа
системы
изначально строится годограф W(jω), а
затем вектор соответствующий данному
годографу не изменяясь по длине
поворачивается на угол .
17
18.
Изпостроения
очевидно,
что
при
некотором годограф может охватить точку
с координатами -1j0 следовательно даже
САР первого порядка с запаздыванием
может быть неустойчива.
18

















 physics
physics








